两相静止坐标系下并网逆变器的重复控制策略

张学广　马　彦　李　瑞　张文杰　徐殿国

(哈尔滨工业大学电气工程及自动化学院　哈尔滨　150001)



两相静止坐标系下并网逆变器的重复控制策略

张学广马彦李瑞张文杰徐殿国

(哈尔滨工业大学电气工程及自动化学院哈尔滨150001)

摘要采用LCL型滤波器的三相PWM并网逆变器在同步旋转坐标系下的数学模型存在耦合项，另外当并网电压不平衡或含低次谐波时，输出电流波形会产生畸变。针对以上问题，提出一种两相静止坐标系下的电流重复控制方法。该方法不需要进行Park变换和解耦计算，可有效降低逆变器并网电流的总谐波畸变。详细给出了重复控制器的参数设计方法，同时考虑了LCL滤波器硬件参数和系统延迟的影响。最后通过仿真和实验验证了理论分析的正确性和控制策略的有效性。

关键词：三相并网逆变器两相静止坐标系重复控制谐波抑制

0引言

电压源型逆变器(Voltage Source Inverter，VSI)是分布式发电系统最关键的部分，其功率因数和输出电流总谐波畸变(Total Harmonic Distortion，THD)直接决定对电网的污染程度，根据国际电工委员会的标准，三相PWM并网逆变器的入网电流THD[1]要低于5%。

为了抑制入网电流谐波，并网逆变器通常采用单电感L型滤波器或LCL型滤波器。在滤波电感值相同且开关频率较低的情况下，LCL型滤波器滤除高次谐波的效果明显好于L型滤波器[2，3]，故本文针对并网逆变器加LCL型滤波器的拓扑结构进行研究，所提方案也同样适用于单电感型滤波器。采用LCL滤波器的并网逆变器有间接电流控制[4，5]和直接电流控制两种方案。间接电流控制将LCL滤波器看成一个电感，电流采样点在逆变器侧的滤波电感上，电流环模型为一阶系统，控制器结构设计简单，但由于实际并网电流受到电网电压与LCL滤波器参数影响，实际并网电流与逆变器输出电流在相位和波形正弦度上有较大误差；直接电流控制系统较复杂，目前的控制方法主要有以下几种。

同步坐标系下的PI控制器设计简单，在电网三相平衡时能获得较好的控制效果，但对周期性的扰动(如电网电压谐波)控制效果并不理想，故不适用于电网电压三相不平衡或含谐波的情况[6]。

两相静止坐标系下的比例谐振(PR)控制[7，8]避免了坐标变换和解耦过程，在控制器的谐振频率处理论上拥有无限大的阻抗，能有效消除谐振频率处的谐波。但当电网电压谐波含量丰富时，需要加入多个不同谐振频率的控制器来滤除各次谐波，PR控制器对离散参数较为敏感，控制器数量增加引起控制系统的延时不可忽略，影响系统的稳定性。

基于内模原理[9，10]的重复控制器类似一个周期性波形发生器，对输入的周期性误差信号逐周期无限制地进行累加。因此，只要控制系统稳定，则可认为稳态误差为零，即反馈波形完全跟随给定波形。重复控制器充分利用了干扰信号的周期性，可有效抑制电网电压谐波等周期性干扰。目前重复控制已广泛应用于单相VSI、不间断电源和有源滤波器中，对于使用LCL型滤波器的三相VSI，文献[11]提出了在同步坐标系下采用PI加重复控制的方案，这样不仅需要复杂的坐标变换和解耦过程，而且未充分发挥重复控制对周期性输入无差跟随这一特点。

本文首先对采用LCL滤波器的并网逆变器建模，分析电网电压谐波和不平衡对并网电流的影响，提出了一种工作于两相静止坐标系下的重复控制方法。所提方案不需要进行坐标变换和解耦工作，在锁相可靠的前提下可有效抑制电网电压不平衡和谐波的影响，显著降低并网电流的THD。而且，当硬件参数固定时控制器的基本参数就已经确定，不需要再进行繁琐的调试工作，大大提高了仿真和实验的效率。根据实际的硬件参数设计了重复控制器，最后通过仿真和实验验证了所提方案的有效性。

1LCL型并网逆变器的建模与分析

三相并网逆变器的拓扑结构如图1所示。图1中，Lg、Li和C分别为LCL滤波器的电网侧电感(电网接口电感)、逆变器侧电感和滤波电容；Rg、Ri和RC分别为Lg、Li和C的等效串连电阻；ej和uj分别为电网电压和逆变器输出端电压；选择网侧电感中电流igj、逆变器侧电感中电流iij和滤波电容两端电压vCj为状态变量(j=a，b，c)，参考方向如图1所示，得到A、B、C三相的状态方程分别为

(1)

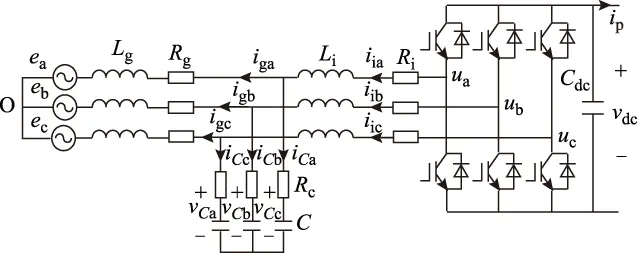
图1　LCL并网逆变器电路拓扑Fig.1　Topology of LCL grid-tied inverter

对式(1)进行拉氏变换后再进行Clarke变换得到两相静止坐标系下的模型为

(2)

由式(2)可看出，状态变量在αβ坐标系下各自独立并无耦合项存在，且α轴与β轴下的状态变量表达式完全一致，因此只需针对一个轴设计控制器即可。由于状态变量均为交流量，采用PI控制器无法实现无静差跟踪，故对式(1)进行拉氏变换后再进行Park变换得到同步坐标系下的数学模型为

(3)

式中，ω0为电网电压角频率。根据式(3)可得到dq坐标系下的系统模型，如图2a所示。显然，基于LCL滤波器的并网逆变在dq轴下的数学模型是一个含多个变量耦合的系统，dq轴下的并网电流不仅受dq轴下逆变器输出电压和电网电压控制，还受ω0Li、ω0C和ω0Lg等交叉耦合量及各种前馈量影响。若直接对dq轴下并网电流进行控制，需要对各交叉耦合量进行前馈解耦，引入的前馈变量太多，使控制器设计变得复杂。当电网电压不平衡或含谐波时，在dq轴下均表现为谐波，而传统的PI控制器对谐波抑制能力差，因此考虑在αβ坐标系下设计控制器。

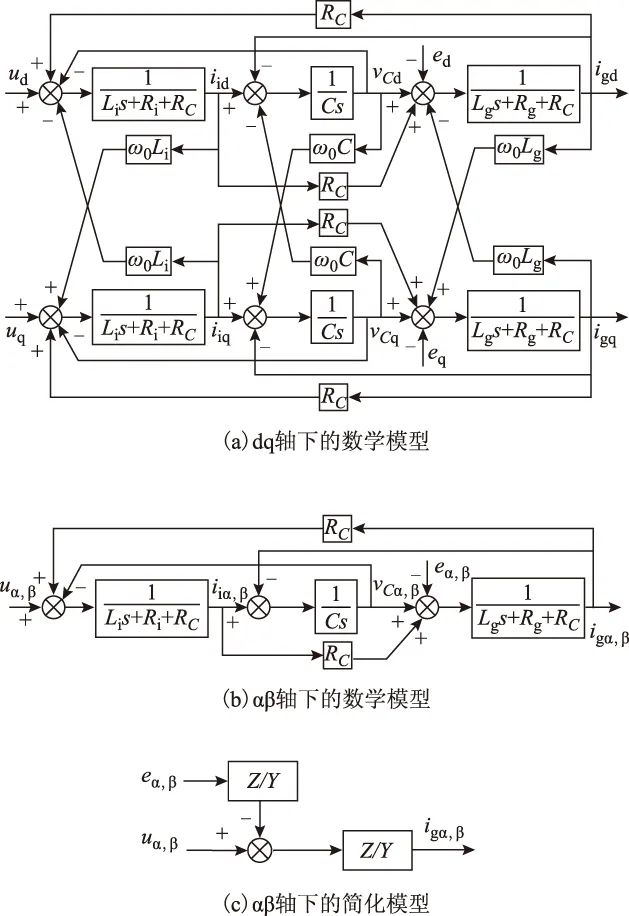
图2　LCL并网逆变器的数学模型Fig.2　Mathematical model of LCL grid-tied inverter

根据式(2)，得到αβ轴下的系统框图如图2b所示。虽然三相系统在αβ轴下相当于两个“独立”的单相，已经不含耦合项，但仍含有许多前馈量，对αβ轴下的模型进一步化简，将逆变器输出电压看作控制量，将逆变器输出电流和滤波电容上的电压作为中间变量。根据式(2)，消去相关中间变量，可得系统简化数学模型为

(4)

式中

此时，得到系统在αβ轴下的简化模型如图2c所示。对比式(3)和式(4)及图2a和图2c，化简后的αβ坐标系下的模型已非常简洁。然而，由于式(4)中各变量均为交流量，使用传统的PI控制器无法做到无静差跟随，无法抑制电网电压谐波和不平衡带来的扰动，因此考虑在αβ轴下使用对周期性输入无差跟随且能抵抗周期性扰动的重复控制方案。

2两相静止坐标系下的重复控制器设计

2.1重复控制策略

嵌入式结构的重复控制原理框图如图3所示。整数N表示系统采样频率fs与指令信号频率f0的比值，N=fs/f0；主前向通道中含有一个N采样周期纯延迟环节z-N，此环节可使控制信号ur具有一定的超前性，从而弥补被控对象中滞后环节和惯性环节造成的滞后，但系统控制快速性受到影响；上方附加的前向通道保留了指令信号的快速通路；Q(z)是考虑重复控制器的稳定性和稳态误差而取的附加函数，可以是一个稍小于1的常数或低通滤波器；P(z)为被控对象的离散传递函数；d为作用在被控对象上的周期性扰动；补偿器C(z)是重复控制器中最重要的部分，它的设计需要针对被控对象P(z)的特性，当重复控制器的内模包含了周期性的指令信号r和扰动信号d时，C(z)的设计需要使被控对象P(z)的输出无静差地跟随指令信号，一般理想的补偿器为C(z)=P-1(z)。

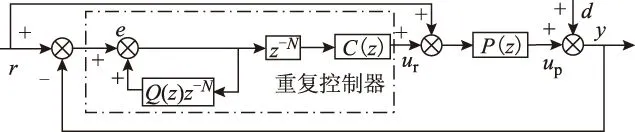
图3　重复控制系统结构框图Fig.3　Structure diagram of repetitive control system

由图3可得到扰动d到误差e的传递函数为

(5)

式中，Q(z)≈1，C(z)P(z)≈1，因此可得到

‖Q(z)-C(z)P(z)‖<1

(6)

式(6)表明Z域上的N个极点均位于单位圆内，即当存在扰动时也可保证系统的稳定性。考虑扰动信号的频率fd是指令信号频率f的整数M倍，即

fd=Mf=Mfs/N，z-N=e-jN2πfd/fs=e-j2πfd/f=e-j2Mπ=1

(7)

进一步可得到

-1+Q(z)z-N≈0

(8)

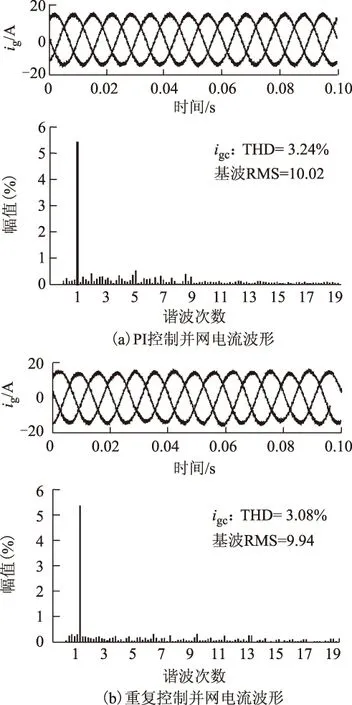
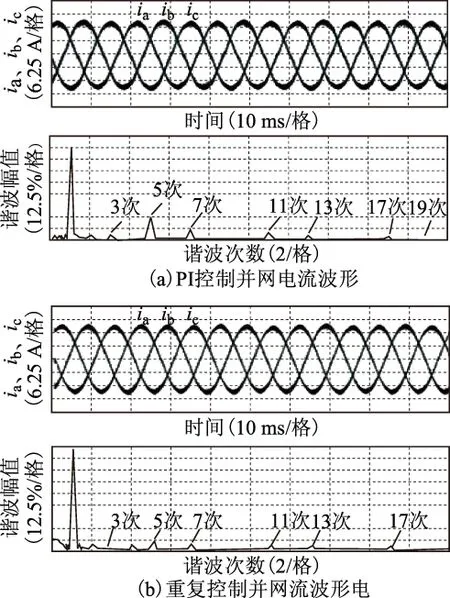
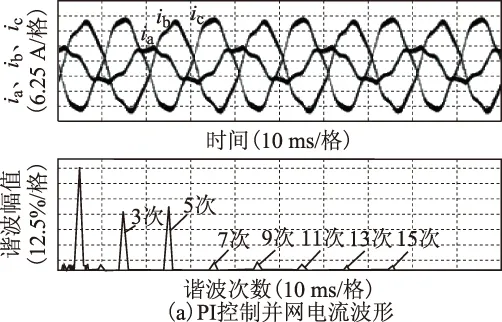
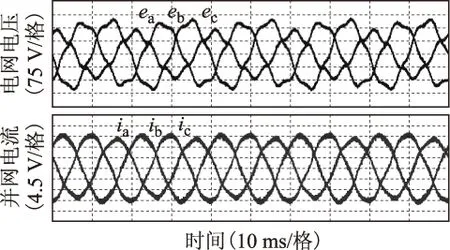
式(8)表明频率为指令信号频率的整数倍的周期性扰动对系统几乎无影响。在并网逆变器系统中，电网电压谐波或不平衡都可看成谐波作用的结果，因此从理论上看，将重复控制器应用于逆变器控制能有效抑制电网电压谐波或不平衡带来的影响。由以上分析可知，只要系统的采样频率fs与输入信号频率f0满足N=fs/f0，包含内模z-N的重复控制器的输出便能无静差地跟随指令信号，且能抵抗频率为指令信号频率整数倍的周期性扰动，非常适用于含谐波扰动的逆变器控制。根据并网逆变器在两相静止坐标系下的简化模型，设计两相静止坐标系下LCL并网逆变器的重复控制策略框图如图4所示。

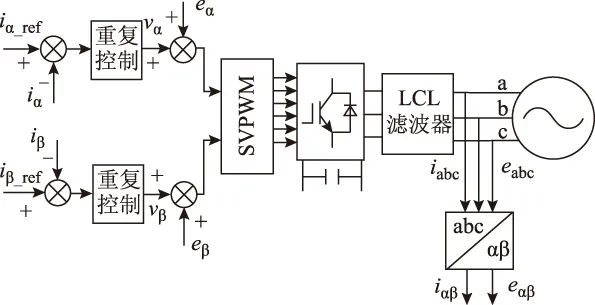
图4　αβ坐标系下并网逆变器重复控制框图Fig.4　Diagram of repetitive control for grid-tied inverter in αβ axes

2.2重复控制器设计

本文提出的两相静止坐标系下重复控制器用于抑制电网电压周期谐波对并网电流的影响，其指令信号的相位及频率由增强型锁相环提供。重复控制器的设计主要包括附加函数Q(z)、补偿器C(z)以及延迟环节z-N的设计。

2.2.1附加函数Q(z)

为保证系统的稳定性，附加函数Q(z)的增益应小于1；当Q(z)为一个稍小于1的常数时，系统存在一定的稳态误差；当Q(z)为低通滤波器时，系统在低频时能做到无静差跟随，高频时仍有稳态误差。FIR滤波器的设计方便且频率特性精确，低频时拥有线性相位特性，选择FIR滤波器作为附加函数可使重复控制器接近于理想特性。出于稳定性考虑，FIR滤波器的截止频率应小于采样频率的1/10。综合考虑快速性、衰减大小和所占内存大小，设计了基于汉宁窗的3阶FIR滤波器，并取截止频率为采样频率的0.08倍，得到Q(z)的表达式为

Q(z)=0.136 1+0.363 9z-1+0.363 9z-2+0.136 1z-3

(9)

2.2.2补偿器C(z)

补偿器C(z)需要根据实际参数设计，仿真和实验使用的参数相同：Li=6 mH，Lg=20 μH，C=20 μF，Ri=0.2 Ω，Rg=0.02 Ω，RC=0.001 Ω。根据式(4)得

(10)

根据图2c，得到被控对象模型为

P(s)=

(11)

由式(11)可看出，被控对象模型是一个三阶的系统，但高次项的系数很小，对低频信号几乎无影响，因此相应的系数极小的项也可忽略，被控对象变为

(12)

根据重复控制器的原理，当C(s)P(s)=1时是最理想的补偿器，但此时C(s)包含微分项，不易于数字实现，故给C(s)添加一个高频极点，得到

(13)

对C(s)进行双线性离散化，采样周期为2×10-4s，得到

C(z)=30.210 4-29.990 4z-1

(14)

一旦并网逆变器系统的硬件参数确定，重复控制器的基本参数就已经确定，无需再进行繁杂的参数调试工作，有效提高了实验效率。

2.2.3延迟环节z-N

观察图3中重复控制器部分，其主前向通道中的纯延迟环节z-N将控制信号延迟了N个采样周期的时间，理想情况下应选取N=fs/f0，此时整个重复控制器的输出既不超前也不滞后，而当N

3仿真及实验结果

为了验证理论分析，使用所设计重复控制器进行仿真和实验，仿真和实验参数一致。除了前文提到的硬件参数，电网线电压有效值Vll=190 V，直流母线电压Vdc=500 V，开关频率与采样频率fswitch=fs=5 kHz。

3.1仿真分析

使用Matlab/Simulink进行仿真，并网电流有效值给定为10 A。分别在电网正常情况和不平衡且含谐波时，对比αβ轴下的重复控制器与dq轴下的PI控制器的控制效果，向电网电压中加入幅值为30%的基波负序和10%的5次正序谐波电压来实现电网电压不平衡和含谐波的情况。采用PI控制和重复控制时的三相并网电流波形及c相电流傅里叶分析如图5所示。

图5　理想电网条件下并网电流仿真波形Fig.5　Simulation results with ideal grid voltage

对比图5a和图5b可发现，在理想电网状态下，在dq坐标系下采用PI控制器与αβ坐标系下采用重复控制的效果基本相同，并网电流的谐波较小，均满足并网标准。观察图6a和图6b可发现，当电网电压不平衡且含有正序谐波时，在dq坐标系下采用PI控制器并网电流发生严重畸变，THD>5%，不满足并网标准；在αβ轴下使用重复控制器的控制效果明显好于在dq轴下使用PI控制器，并网电流波形无明显畸变，THD仅为4.33%。

图6　电网谐波条件下并网电流仿真波形Fig.6　Simulation results with harmonics in grid voltage

3.2实验验证

实验平台硬件参数与仿真一致，分别在电网电压理想和不平衡且含谐波条件下对两种控制方法进行对比实验，利用可编程交流电源向电网电压中加入30%的基波负序和10%的5次正序谐波来实现不平衡和含谐波的情况。理想电网电压条件下，使用PI控制和重复控制策略的实验波形如图7所示。图7a为在dq轴下使用PI控制器的并网电流，实验波形与仿真效果基本一致，并网电流波形三相平衡且正弦度好，谐波含量较少；图7b为αβ轴下使用重复控制器时的并网电流波形，相比于在dq轴下使用PI控制器的电流，在αβ轴下使用重复控制器的电流谐波更小，尤其是低次谐波含量，两种控制策略的谐波含量均满足并网标准。

图7　理想电网条件下并网电流实验波形Fig.7　Experimental results with ideal grid voltage

电网电压不平衡且含谐波条件下，使用PI控制和重复控制策略的实验波形如图8所示。图8a为采用传统PI控制器时的并网电流波形，在不平衡情况下电网电压的负序分量不为零，导致dq坐标系下存在2倍工频的交流量，由于PI无法实现对交流量的无静差跟踪，所以此时控制效果较差，可观察到三相电流严重不平衡且畸变较大。图8b为采用所提重复控制器时的并网电流波形，重复控制器对周期扰动信号有很好的抑制效果，不平衡且含谐波的电网电压可被视为在理想电网电压的基础上加入周期性扰动信号，因此可利用重复控制器来抑制电网电压谐波对入网电流的影响，观察图8b可发现，此时三相电流基本平衡，且正弦度较好，谐波含量相比PI控制时减少，尤其是3次和5次谐波，满足并网电流的要求。

图8　电网谐波不平衡条件下并网电流实验波形Fig.8　Experimental results of grid current with harmonics contained in unbalanced grid voltage

通过改变电流给定的角度可实现有功和无功的调节。图9和图10为不同电流角度给定时电网电压和并网电流的波形，图9中电流角度给定与电网电压相角相同，图10中电流角度给定超前电网电压相角90°。对比图9和图10可看出，电流控制效果不受影响，所提重复控制策略能有效实现有功和无功的解耦控制。

图9　电流角度给定超前为零时实验波形Fig.9　Experimental results with current angle reference without phase lead

图10　电流角度给定超前90°时实验波形Fig.10　Experimental results with current angle reference 90° phase lead

4结论

本文针对基于LCL型滤波器的并网逆变器dq轴下耦合严重和PI控制器对电网电压不平衡和谐波抑制能力差的特点，在分析逆变器的拓扑结构和数学模型的基础上，提出αβ轴下的重复控制方案。所提方法不需要进行坐标变换和解耦过程，在锁相可靠的基础上，能在无静差跟随给定信号电流的同时，消除各种频率为50 Hz整数倍的周期性扰动。此外，由于控制器的设计是针对具体硬件设备，所以一旦硬件参数确定，控制器的基本参数就已确定，无需进行繁琐的参数调试，缩短了实验周期。仿真和实验结果验证了理论分析的正确性，表明了此方法能有效抑制电网电压不平衡和谐波带来的谐波电流，适用于电网电压畸变严重的三相并网逆变器。

参考文献

[1]IEEE519—1992.Recommended practices and requirements for harmonic control in electrical power systems[S].[2]刘飞，查晓明，段善旭.三相并网逆变器LCL滤波器的参数设计与研究[J].电工技术学报，2010，25(3)：110-116.

Liu Fei，Zha Xiaoming，Duan Shanxu.Design and research on parameter of LCL filter in three-phase grid-connected inverter[J].Transactions of China Electrotechnical Society，2010，25(3)：110-116.

[3]彭双剑，罗安，荣飞，等.LCL滤波器的单相光伏并网控制策略[J].中国电机工程学报，2011，31(21)：17-124.

Peng Shuangjian，Luo An，Rong Fei，et al.Single-phase photovoltaic grid-connected control strategy with LCL filter[J].Proceedings of the CSEE，2011，31(21)：17-124.

[4]Teodorescu R，Blaabjerg F，Borup U，et al.A new control structure for grid-connected LCL PV inverters with zero steady-state error and selective harmonic compensation[C]//Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition，Anaheim，California，2004，1：580-586.

[5]李玉玲，鲍建宇，张仲超.间接电流控制可调功率因数电流型PWM变流器[J].中国电机工程学报，2007，27(1)：49-53.

Li Yuling，Bao Jianyu，Zhang Zhongchao.Indirect current control adjustable power factor current source pwm converter[J].Proceedings of the CSEE，2007，27(1)：49-53.

[6]王斯然，吕征宇.锂电池馈电并网系统进网电流谐波抑制方法[J].电工技术学报，2009，33(19)：90-95.

Wang Siran，Lü Zhengyu.A harmonics suppression method for lithium battery grid integration system[J].Transactions of China Electrotechnical Society，2009，33(19)：90-95.

[7]Twining E，Holmes D G.Grid current regulation of a three-phase voltage source inverter with an LCL input filter[J].IEEE Transactions on Power Electronics，2003，18(5)：888-895.

[8]Yang Shuitao，Lei Qin，Peng Fangzheng，et al.A robust control scheme for grid-connected voltage-source inverters[J].IEEE Transactions on Industrial Electronics，2012，58(1)：202-212.

[9]张凯，鹏力，熊健，等.基于状态反馈与重复控制的逆变器控制技术[J].中国电机工程学报，2006，26(10)：56-62.

Zhang Kai，Peng Li，Xiong Jian，et al.State-feedback-with-integral control plus repetitive control for PWM inverters[J].Proceedings of the CSEE，2006，26(10)：56-62.

[10]Chen D，Zhang J，Qian Z.An improved repetitive control scheme for grid-connected inverter with frequency-adaptive capability[J].IEEE Transactions on Industrial Electronics，2013，60(2)：814-823.

[11]王斯然，吕征宇.LCL型并网逆变器中重复控制方法研究[J].中国电机工程学报，2010，30(27)：69-75.

Wang Siran，Lü Zhengyu.Research on repetitive control method applied to grid-connected inverter with LCL filter[J].Proceedings of the CSEE，2010，30(27)：69-75.

作者简介

张学广男，1981年生，博士，副教授，研究方向为可再生能源发电技术。

E-mail：zxghit@126.com(通信作者)

马彦男，1992年生，硕士研究生，研究方向为三相PWM变流器控制技术。

E-mail：mylssp@163.com

Repetitive Control Strategy for Grid-Connected Converters in Stationary Frame

Zhang XueguangMa YanLi RuiZhang WenjieXu Dianguo

(Department of Electrical EngineeringHarbin Institute of TechnologyHarbin150001China)

AbstractIn the synchronous rotating frame，coupling exists in the mathematical model of the grid-connected inverters adopting LCL filters.And serious distortion occurs in the inverter output current under unbalanced grid voltage or with low order harmonics in the grid voltage.Considering problems mentioned above，this paper presents a current repetitive control strategy in the stationary frame.The proposed method does not require the Park transformation or the decoupling process.It is able to effectively reduce the total harmonic distortion of the injected grid current.The specific design method of the repetitive controller is provided，considering the hardware parameters of the LCL filter and the influence of the system delay.Simulation and experimental results are presented in the end，which verifies the validity of the theoretical analysis and the effectiveness of the proposed method.

Keywords：Grid-connected inverter，stationary frame，repetitive control，harmonic suppression

中图分类号：TM464

国家自然科学基金(51107020、51577040、51237002)和台达电力电子科教发展基金资助项目。

收稿日期2015-02-10改稿日期2016-03-10