交直流混合电力系统的安全校正策略

毕如玉　林　涛　陈汝斯　徐遐龄　叶　婧

(1.武汉大学电气工程学院　武汉　430072 2.华中电力调控分中心　武汉　430077)



交直流混合电力系统的安全校正策略

毕如玉1林涛1陈汝斯1徐遐龄2叶婧1

(1.武汉大学电气工程学院武汉430072 2.华中电力调控分中心武汉430077)

摘要随着交直流混合电力系统的迅速发展，直流闭锁或线路故障引发系统连锁故障的风险增加，故需要根据电网运行状态采取相应的控制措施避免潮流进一步过载。在智能电网背景下，考虑将直流和可控串联补偿器(TCSC)也作为控制措施以进一步减少负荷切除量。制定安全校正策略常用的方法有灵敏度法和优化规划法。灵敏度法便于在线切机切负荷控制，分析了直流功率和TCSC电抗值的支路潮流灵敏度是控制量的函数并非定值，故在交直流混合电力系统的安全校正策略制定中应用灵敏度法有一定困难。针对优化规划法优化变量多、计算时间长、难以在线实施，提出采用启发式搜索原理缩减优化变量数量的优化规划法，该方法基于负荷转移因子(LSF)筛选出对待调节支路控制效果最好的发电机和负荷节点，将这些节点的功率与直流功率以及TCSC电抗值一同作为优化变量，以负荷总切除量最小即经济性最佳为目标函数建立优化模型并采用智能优化算法求解，能够在较短时间内得到安全校正方案。基于改造的IEEE30节点算例系统，通过与不采用启发式搜索以及不考虑将直流功率和TCSC电抗值作为优化变量得到的结果相比较，该方法的有效性及优越性得到验证。

关键词：连锁故障安全校正可控串联补偿器

0引言

近年来，随着超/特高压远距离直流输电工程以及灵活交流输电系统(Flexible AC Transmission System，FACTS)的投运，电网的大功率、远距离输送能力得到提高，并且输送功率也更接近热极限功率[1]。但线路输送功率的增加也使得交流线路发生故障被切除或直流线路闭锁导致的潮流转移更加严重，若不能及时采取安全校正控制，转移的潮流将造成其他线路潮流过载被切除进而发生连锁故障[2-5]。安全校正控制是指采取有效措施，在故障初期尽快消除电网中的各种越限现象，将越限的影响范围和损失程度降至最低。因此，系统能否安全、稳定运行主要取决于安全校正策略是否正确、合理。

目前，已有的安全校正策略主要采用灵敏度法和优化规划法。灵敏度法通过计算控制变量对支路潮流变化的关系，根据支路潮流的越限量反推出控制变量的调整量以达到消除支路潮流越限的目的[6-9]，便于操作实施，但无法处理系统运行中的一些安全约束问题，往往导致平衡机组越限，也可能出现将一部分越限拉回到约束以内的同时又有一部分新的越限出现。在交流系统方面对灵敏度因子的分析已经比较完备，并且在稳定性分析等很多方面都有比较广泛的应用[10，11]。优化规划法通过求解数学模型得出控制方案，文献[12]提出了基于节点不平衡功率的潮流转移控制算法，通过将节点不平衡功率作为优化目标，避免了常规人工智能优化算法中必须先满足潮流等式后再优化求解的弊端；文献[13]提出了一种对发电机及切负荷点进行分组，然后利用分组信息对已优化的发电机加出力总量和减出力总量以及切负荷总量进行合理分配的有功转移潮流控制策略。优化规划法可设置复杂的约束条件和合理的目标函数，故而有较好的安全性和经济性，但因为全网发电机和负荷节点多，即优化变量众多，导致优化空间维数高，计算时间长甚至存在收敛性问题。

在智能电网的框架下，具有相当规模的直流输电走廊在区域间实现互联，并且灵活交流输电系统[14]也投入应用。在这样的背景下，通过调整直流功率和FACTS装置也可达到控制潮流的目的。针对将直流功率和可控串联补偿器(Thyristor Controlled Series Capacitor，TCSC)的电抗值也作为校正控制手段的问题，本文推导出直流功率和TCSC电抗值对交流线路的支路潮流灵敏度会随着直流功率和TCSC电抗值的改变而改变，难以反推出控制量的调整量的结论。基于以上分析，本文采用优化规划法，针对优化规划法优化变量多、优化时间长的弊端，提出采用启发式搜索原理缩减优化变量的优化规划法安全校正策略。

1灵敏度法调控直流和TCSC的局限性

支路潮流灵敏度是指节点注入有功功率对支路有功潮流变化的灵敏度[15]。根据发电量转移分配系数GSDF[16]的定义，节点k注入单位有功功率对支路i-j有功潮流的灵敏度可写为

(1)

式中，Pij为支路i-j有功功率；Pk为节点k注入有功功率；Xik、 Xjk分别为节点电抗阵X中对应的元素；xij为支路i-j电抗。

1.1直流功率对交流线路的有功潮流灵敏度分析

在交直流混合输电系统中，由于直流线路可以迅速地调整输送功率，故当某些交流线路潮流越限时，希望通过调整直流线路功率来降低越限支路的潮流。将直流线路a-b对交流线路i-j有功潮流的灵敏度定义为

(2)

将直流线路a-b等效为线路开路、a端注入功率Pab，b端负荷功率Pab。 改变直流线路的输送功率Pab，相当于节点导纳矩阵Y中b点的自导纳改变，进而求逆得到的节点电抗阵X中每个元素都将改变。因为Pab变化将导致Xia和Xja变化，故Sij-ab会随直流功率Pab的变化而变化。

1.2TCSC电抗值对交流线路的有功潮流灵敏度分析

当交流线路潮流越限时，可以通过调整TCSC电抗值来改善潮流[17]。假设某线路a-b装有TCSC，即线路电抗xab=xLine+xTCSC。则xab对支路i-j有功潮流的灵敏度Sij-ab可通过式(3)计算。

(3)

式中，Pa为节点a注入有功功率。根据直流潮流算法原理[18]有

(4)

式中，θk为k点电压相角。将Pa展开为两部分之和，第一部分是与xab无关的表达式c1，第二部分为与xab有关的表达式c2，对xab求偏导数得

(5)

将式(5)和式(1)带入Sij-ab的表达式可得

(6)

式中

从式(6)可以看出Sij-ab会随着线路电抗xab的改变而改变。

综上所述，在交直流混合输电系统中，由于直流功率和TCSC电抗值对交流线路的有功灵敏度会随直流功率和TCSC电抗值的调整而改变，使得难以根据灵敏度法反推出控制变量的调整量，建立基于灵敏度法推导出交直流混合系统中的安全校正策略存在困难。

2基于启发式搜索原理的安全校正策略

针对灵敏度法难以应用于交直流混合系统的安全校正策略制定以及优化规划法优化变量多、难以在线应用的问题，本文研究了基于启发式搜索原理缩减优化变量数量的优化规划法安全校正策略。

2.1待调节支路的确定

在确定优化变量前首先需要确定故障后或直流闭锁后哪些支路发生潮流过载，即确定待调节支路。

采用收敛性较好的柔性潮流算法计算故障后或直流闭锁后的潮流，得到故障后潮流计算值。用非故障支路的潮流计算值减去其潮流上限值，筛选出发生潮流越限的支路，将这些支路作为待调节支路。

2.2安全校正优化模型

2.2.1优化变量的选取

对于实际电力系统，节点数众多，逐一调整所有的发电机和负荷既费时又费力，而且在优化问题中，优化变量越多、计算量越大、所需时间就越长，不便于在线实施。针对这种情况，基于启发式搜索原理缩减优化变量。启发式搜索的原理是只选择对待调节支路的潮流调节效果最好的控制量作为优化变量，这样可大大减少优化的维数，提高优化效率，缩短优化时间。

1)连续型变量x的选取。首先计算出所有发电机对待调节支路A的负荷转移因子(Load Shift Factor，LSF)[19]，并从大到小排序，然后采用聚类算法[20，21]聚类出对该待调节支路潮流调节效果最好的发电机节点集合xA。采用聚类算法的原因是避免因主观评价哪些发电机节点属于调节效果最好的一类而对优化结果造成影响。然后依次聚类出对第i个待调节支路潮流调节效果最好的发电机节点集合xi，对这些发电机节点集合取并集即得到对所有待调节支路调节效果最优的发电机节点的集合xgen。将这些发电机节点的有功、无功功率和直流线路功率以及TCSC电抗值一同作为连续型变量x。

2)二元型变量y的选取。同样基于LSF，聚类得到对每条待调节支路的潮流调节效果最好的负荷节点集合并取并集得到yk。文中负荷节点在实际中指变电站，而负荷指变电站的每条出线，因为变电站出线上的功率无法实现连续调节，故将变电站集合yk中每条出线的切除与否作为独立的0-1二元型优化变量y，1表示保留该出线，0表示断开该出线。

2.2.2目标函数

为了尽可能提高安全校正策略的经济性，将目标函数设置为负荷有功总切除量最小。

(7)

式中，n为二元型变量数量；PLi为二元型变量i的有功功率；yi为二元型变量i的值，0表示该负荷被切除，1表示该负荷被保留。

2.2.3约束条件

为了保证安全校正策略的安全性，设置以下约束：

1)常规约束：节点电压约束、发电机有功上下限约束、发电机无功上下限约束、负荷上下限约束、支路电流和潮流约束、功率因数约束和发电机视在功率约束。

2)频率约束：对于容量较小的电网，有可能因为切负荷量和切机量的不平衡而导致频率出现较大偏移，为了防止安全校正策略导致系统有功不平衡，故加入频率约束，系统频率偏差不得超过±0.1 Hz。

3)TCSC电抗值约束：TCSC装置电抗值XTCSC应满足上下限约束，否则可能引发次同步振荡。故设置约束为

Xmin≤XTCSC≤Xmax

(8)

4)直流线路功率约束：直流线路传输的功率应满足上下限约束。考虑到柔性直流输电技术可以实现功率自由双向传递[22]，针对采取柔性直流输电的线路输送功率约束为

-PDmax≤PD≤PDmax

(9)

若是常规直流，则约束为

PDmin≤PD≤PDmax

(10)

2.3混合型优化模型的求解

本文采用改进的智能优化算法和改进的柔性潮流算法进行安全校正优化模型的求解。采用改进PGSA算法的原因是该算法效率高，可以缩短优化时间；采用柔性潮流算法[23，24]是因为该算法可以在非工频情况下计算潮流且可以计算系统频率。本文对柔性潮流算法做了改进使其可以近似计算交直流混合电力系统的潮流。以下分别对两种算法做简要介绍。

2.3.1改进模拟植物生长算法

模拟植物生长算法(Plant Growth Simulation Algorithm，PGSA)具有参数设置简单、全局寻优能力较强等优点[25，26]，但是原始PGSA算法只适用于整数规划问题，且由于其搜索步长为定值并且随机选择新生长点，因此算法效率较低。本文采用改进PGSA算法[27]对安全校正方案进行求解。改进PGSA算法可以处理混合型规划问题；通过采用变步长的搜索策略，改进PGSA算法的效率不受初值选取的影响；通过将云模型理论应用于新生长点的选取，改进PGSA算法在上一轮的最优生长点附近寻求新的生长点，让植物始终朝着最优解的方向生长，从而提高了算法的收敛速度。

2.3.2改进柔性潮流算法

为了避免故障后出现较大功率缺额导致常规潮流计算不收敛，采用可以在非工频下计算潮流的柔性潮流算法。为计算交直流混合系统的潮流，本文对柔性潮流算法进行了一定改进。对直流线路做等效处理，近似认为送端输出恒功率PD、受端注入恒功率PD。将直流功率PD加入潮流等式约束中，则柔性潮流算法的等式约束改进为

(11)

式中，PGi、QGi分别为接于节点i的发电机支路的有功功率和无功功率；PLi、QLi分别为接于节点i的负荷支路的有功功率和无功功率；PNi、QNi分别为接于节点的网络支路的有功功率和无功功率；PD为直流功率，送端为正值，受端为负值。

3算例验证

3.1算例说明与故障设置

安全校正方案的验证基于IEEE30节点改造算例，IEEE30节点标准数据见文献[28]。本文对算例进行如下改造：假设节点4和节点30各有3个负荷，将该节点的负荷总有功和无功按照1∶2∶3的比例分配给这3个独立负荷(yi-1、yi-2和yi-3)；设置直流线路为线路31(节点22-节点24)，功率传输方向为从节点22到节点24，初始传输功率为0.2 (pu)；设置线路37(节点27-节点30)装有TCSC装置。改造后的算例系统包含30个节点，40条交流线路，1条直流线路。本文的优化时间均指在CPU i7-3770K和8G内存配置下的运行时间。

电力系统结构脆弱性是从电网结构角度反映电网抵抗连锁故障的能力。基于文献[29]所述方法对算例电网进行分析得到结构上最脆弱的线路为线路1(节点1-节点2)，即该线路故障最容易造成连锁故障，故以该线路为例设置故障进行算例验证。本文所述的实施步骤对其余线路故障同样适用。

3.2非启发式搜索的优化结果

3.2.1优化变量

非启发式搜索的优化变量有39个，为系统中所有发电机和负荷的有功和无功功率、直流线路功率和TCSC元件的电抗值，以系统故障前优化变量的值作为初始值。

为了体现直流和TCSC的调控效果，设置3组场景：①场景1：优化变量仅为发电机和负荷功率，不含直流功率和TCSC电抗值；②场景2：在场景1的基础上，优化变量加入直流功率和TCSC电抗值，但不允许直流功率反转；③场景3：在场景2的基础上，允许直流功率反转。

3.2.2优化结果

基于2.2节的优化模型进行优化计算，得到的优化结果如表1所示。

表1　非启发式搜索的优化结果

3组场景下的安全校正策略对潮流的调控效果如表2所示。由于算例系统中线路数量较多，限于篇幅，仅列出故障后潮流越限的线路2、4，以及故障后潮流裕度较小的线路7、9、15的潮流结果。

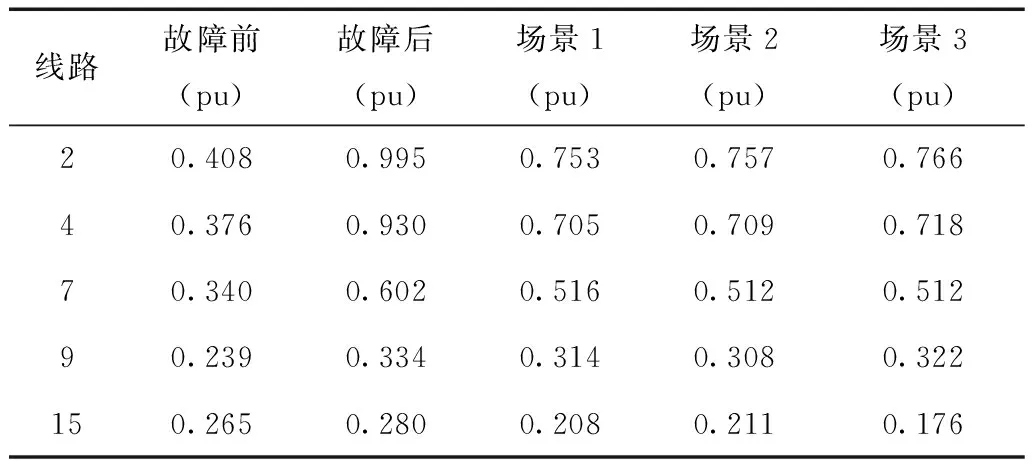
表2　非启发式搜索的潮流结果

对3组优化结果进行分析，不将直流和TCSC作为调控手段的场景1优化时间最长且负荷切除量最大；将直流和TCSC作为调控手段的场景2和场景3优化时间相当，且允许直流反转的场景3负荷切除量更小。从潮流结果中可以看出3组场景下的安全校正策略均能将越限支路潮流控制到安全范围，且降低重载线路的潮流，验证了方案的有效性。

3.3启发式搜索的优化结果

3.3.1优化变量

启发式搜索的优化变量由39个缩减为17个。根据3.1节和3.2节的方法确定的连续型优化变量为：发电机节点1、5、13的有功和无功功率；直流线路功率；TCSC元件的电抗值。0-1二元型优化变量为负荷3、4-1、4-2、4-3、26、29、30-1、30-2、30-3的有功和无功功率。

3.3.2优化结果

为了与非启发式搜索的结果进行对比，场景4、场景5和场景6分别对应场景1、场景2和场景3。得到的优化结果如表3所示，3组场景下的安全校正策略对潮流的调控效果如表4所示。

对3组优化结果进行分析，结论和采用非启发式搜索相似，将直流和TCSC也作为调控手段的场景的负荷切除量更少，优化时间也更短，并且3组方案均具有良好的有效性。

对IEEE30节点改造算例系统的故障后、场景3和场景6三种状态进行了电力系统分析综合程序(Power System Analysis Software Package，PSASP)的校核。对比了3组场景下各条线路有功潮流的柔性潮流计算值与PSASP仿真值，发现两者的结果非常接近，验证了本文潮流算法及优化结果的正确性。还存在一定误差是因为PSASP的潮流模型中没有计入发电机和负荷的有功-频率静特性，但是由于算例中的频率偏移较小，所以误差也较小。

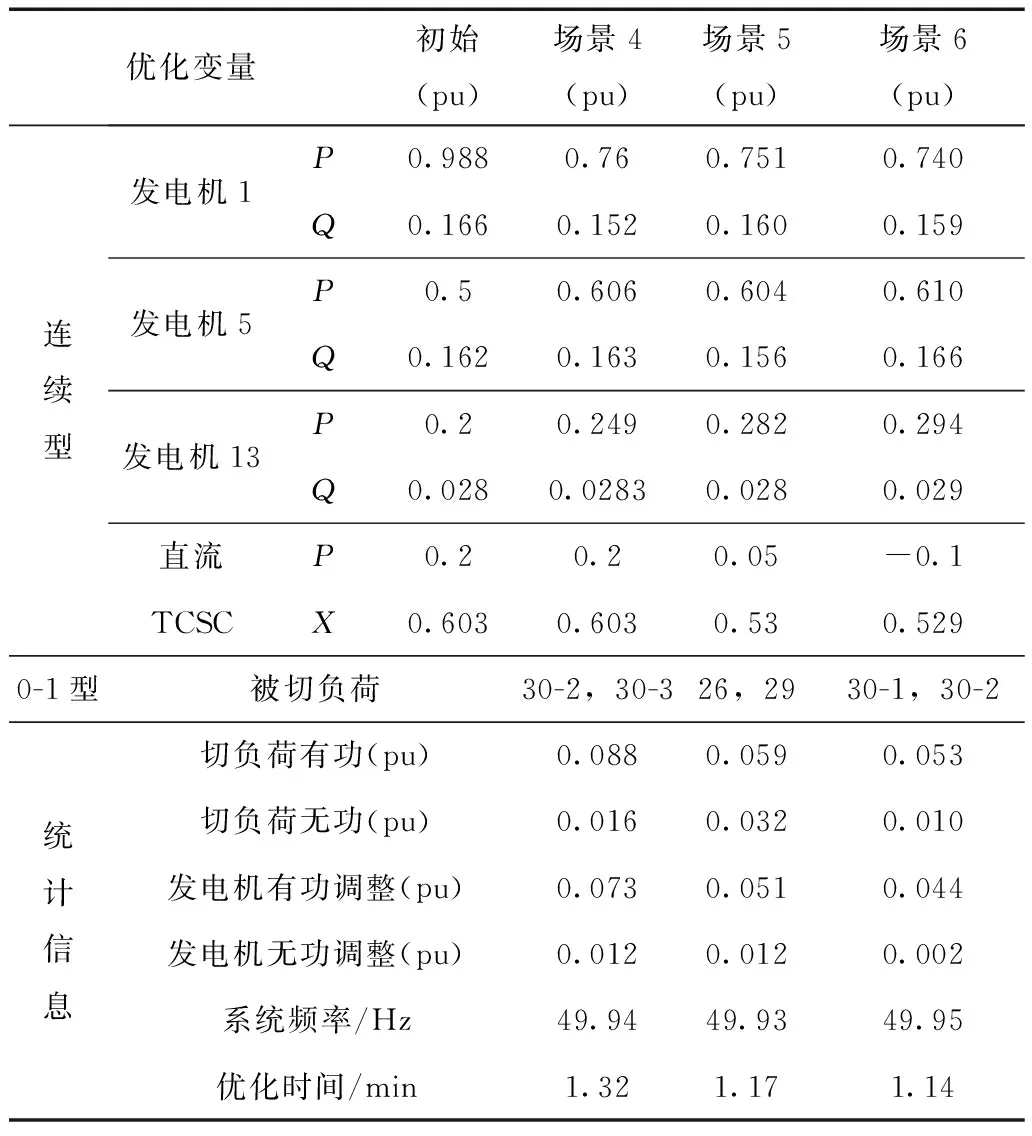
表3　启发式搜索的优化结果

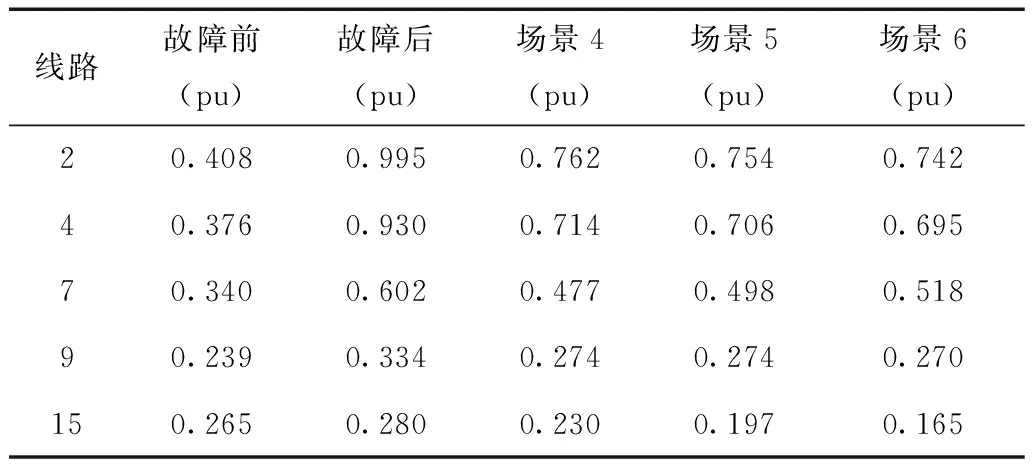
表4　启发式搜索的潮流结果

3.4本文方法和常规方法对比分析

前文已经验证了本文方法的有效性，本节主要对比分析本文方法相对于不考虑调控直流功率和TCSC电抗值以及不采用启发式搜索的安全校正策略的优越性。

为了验证调整直流功率和TCSC电抗值的优越性，将非启发式搜索和启发式搜索得到的结果分别进行横向对比，即场景1比场景2和场景3、场景4比场景5和场景6。从优化时间和切负荷量看，调整直流和TCSC时优化时间略有缩短、切负荷量也更小，说明这两种控制手段调控效果良好，使优化更快收敛且少切负荷。为了验证直流功率反转的调节效果，将场景2比场景3、场景5比场景6，发现在该算例中直流功率反转也可以减小切负荷量。因为经过推导，本算例中直流线路功率对待调节支路的有功潮流灵敏度是正值，即减小直流线路功率可以减小越限支路功率，所以直流功率反转可以相应减少切负荷量，说明在这种情况下进行优化计算时可以考虑将直流反转以减少负荷损失量。

为了验证采用启发式搜索的优越性，将非启发式搜索和启发式搜索得到的结果进行纵向对比，即场景1比场景4、场景2比场景5、场景3比场景6。从优化时间看，场景4-6的优化变量是场景1-3的0.44倍，优化时间约是场景1-3的0.5倍；从切负荷量看，场景4-6的切负荷量均小于其对应的场景。这就说明在采用自然收敛作为优化结束判据的情况下，采用启发式搜索的经济性优于非启发式搜索方法。这是因为启发式搜索缩减了优化变量，降低了搜索维度、缩小了搜索范围，进而提高了搜索效率，使得可以在更短的时间内优化出更好的结果。由于本文算例较小，两种方法的优化变量个数相差不大，故而优化时间缩短有限。若将本文方法应用于实际大电网，优化变量数量将有很大差别，优化效率也将显著提升，离线计算时可以在短时间内得出安全校正方案，也为安全校正方案的在线计算提供了新的思路。

4结论

在智能电网背景下，本文提出将直流功率和TCSC电抗值也作为控制手段的优化规划法安全校正策略，并基于启发式搜索原理缩减优化变量数量以缩短优化时间。该安全校正策略以对待调节支路调节效果最好的发电机和负荷功率以及直流功率和TCSC电抗值为优化变量，以负荷总切除量最小为目标函数建立优化模型，并基于改进模拟植物生长算法进行优化计算，得出安全校正方案。基于改造的IEEE30节点算例对本文方法进行验证，得到如下结论：

1)将本文安全校正方案分别与不采用启发式搜索和不将直流功率和TCSC电抗值作为优化变量的安全校正方案相比，采用本文方法得到的安全校正方案负荷切除量更小、具有更好的经济性。

2)与结论1)同等条件下，本文提出的方法能更迅速地得到安全校正方案，有效避免了常规优化类方法优化时间过长的弊端。

3)与不采用启发式搜索的安全校正方案相比，本文方案所需调整的发电机和负荷少，避免了常规优化类方法调整设备可能过多的弊端。

本文方法能够缩短安全校正方案离线计算时间，也为安全校正方案的在线计算提供了新的思路，对避免连锁故障发生具有重要的参考价值。后续将进一步探索对多条待调节支路的调节效果最好的发电机和负荷节点的集合取交集以进一步减少优化变量的个数、缩短优化时间。

参考文献

[1]Edris A.Facts technology development：an update[J].IEEE Power Engineering Review，2000，20(3)：4-9.

[2]王英英，罗毅，涂光瑜，等.电力系统连锁故障的关联模型[J].电工技术学报，2012，27(2)：204-209.

Wang Yingying，Luo Yi，Tu Guangyu，et al.Correlation model of cascading failures in power system[J].Transactions of China Electrotechnical Society，2012，27(2)：204-209.

[3]Lai Y C，Motter A E，Nishikawa T.Attacks and cascades in complex networks[R].Lecture Notes in Physics，2004，650：299-310.

[4]王增平，李刚，任建文.基于前K最短路径的输电断面搜索新算法[J].电工技术学报，2012，27(4)：193-201.

Wang Zengping，Li Gang，Ren Jianwen.A new search algorithm for transmission section based on K shortest paths[J].Transactions of China Electrotechnical Society，2012，27(4)：193-201.

[5]Latora V，Marchiori M.Vulnerability and protection of infrastructure networks[J].Physical Review E，2005，71(1)：015103.

[6]苗峰显，白雪峰，郭志忠.支路潮流越限控制的虚拟支路法[J].电力系统自动化，2009，33(14)：32-36，65.

Miao Fengxian，Bai Xuefeng，Guo Zhizhong.A virtual branch method for branch power flow off-limit analysis[J].Automation of Electric Power Systems，2009，33(14)：32-36，65.

[7]贾宏杰，穆云飞，余晓丹.基于直流潮流灵敏度的断面潮流定向控制[J].电力系统自动化，2010，34(2)：34-38.

Jia Hongjie，Mu Yunfei，Yu Xiaodan.Directional control method to interface power based on DC power flow and sensitivity[J].Automation of Electric Power Systems，2010，34(2)：34-38.

[8]Wang Pengxiang，Liu Wenying，Liu Zhengyi，et al.Application of machine learning methods in active power security correction of power system[C]//International Conference on Electrical and Control Engineering，Wuhan，2010：476-479.

[9]李海涛，孙闻，赵兵，等.基于交流灵敏度的在线安全控制策略[J].电力系统及其自动化学报，2012，24(1)：32-36.

Li Haitao，Sun Wen，Zhao Bing，et al.Online security control analysis based on sensitivity method[J].Proceedings of the CSU-EPSA，2012，24(1)：32-36.

[10]FerreirA C M M，Pinto J A D，Barbosa F P M.Transient stability assessment of an electric power system using trajectory sensitivity analysis[C]//Proceedings of 39th International Universities Power Engineering Conference，Bristol，2004，2：1091-1095.

[11]Zarat L A L，Castro C A.Fast computation of security margins to voltage collapse based on sensitivity analysis[J].IEE Proceedings：Generation，Transmission and Distribution，2006，153(1)：35-43.

[12]沈晓东，刘俊勇，刘彦.基于节点不平衡功率的粒子群潮流转移控制算法[J].电力系统自动化，2012，36(7)：1-5，70.

Shen Xiaodong，Liu Junyong，Liu Yan.A power flow transferring control algorithm based on node lopsided powers using particle swarm optimization[J].Automation of Electric Power Systems，2012，36(7)：1-5，70.

[13]姜臻，苗世洪，刘沛，等.一种基于粒子群优化算法的转移潮流控制策略[J].电力系统自动化，2010，34(18)：16-20，31.

Jiang Zhen，Miao Shihong，Liu Pei，et al.A particle swarm optimization based power flow transferring control strategy[J].Automation of Electric Power Systems，2010，34(18)：16-20，31.

[14]黄柳强，郭剑波，卜广全，等.FACTS协调控制研究进展及展望[J].电力系统保护与控制，2012，40(5)：138-147.

Huang Liuqiang，Guo Jianbo，Bu Guangquan，et al.Research progress and prospect of FACTS coordinated control[J].Power System Protection and Control，2012，40(5)：138-147.

[15]陈曦.基于灵敏度方法的电网安全校正策略研究[D].保定：华北电力大学，2011.

[16]顾乃炎，侯志俭.几种快速确定发电机分配系数的方法[J].电网技术，1999，23(6)：40-43.

Gu Naiyan，Hou Zhijian.Fast determination methods of generator distribution factors[J].Power System Technology，1999，23(6)：40-43.

[17]李立，鲁宗相，周双喜.典型FACTS设备对连锁故障风险影响研究[J].电力系统保护与控制，2012，40(3)：1-7.

Li Li，Lu Zongxiang，Zhou Shuangxi.Research on the effect of typical FACTS devices on cascading failure risk[J].Power System Protection and Control，2012，40(3)：1-7.

[18]赖敏榕.电网静态安全有功校正策略研究[D].北京：华北电力大学，2007.

[19]吴杰康，李月华，张宏亮，等.负荷转移因子及其在网损计算中的应用[J].现代电力，2008，25(3)：8-12.

Wu Jiekang，Li Yuehua，Zhang Hongliang，et al.Calculation and application of load shift factor of power systems[J].Modern Electric Power，2008，25(3)：8-12.

[20]陈志强，刘钊，张建辉.聚类分析中PAM算法的分析与实现[J].计算机与现代化，2003，9(9)：1-3，6.

Chen Zhiqiang，Liu Zhao，Zhang Jianhui.Analysis and implementation of PAM algorithm[J].Computer and Modernization，2003，9(9)：1-3，6.

[21]王开军，李晓.基于有效性指标的聚类算法选择[J].四川师范大学学报(自然科学版)，2011，34(6)：915-918.Wang Kaijun，Li Xiao.Selection of clustering algorithms based on a validity index[J].Journal of Sichuan Normal University(Natural Science)，2011，34(6)：915-918.

[22]李爽，王志新，王国强.海上风电柔性直流输电变流器P-DPC控制研究[J].电工技术学报，2013，28(2)：264-270.

Li Shuang，Wang Zhixin，Wang Guoqiang.Predictive direct power control strategy for offshore wind power VSC-HVDC converter[J].Transactions of China Electrotechnical Society，2013，28(2)：264-270.

[23]刘宪林，陈楠，苏向敬，等.电力系统柔性潮流[J].电力自动化设备，2009，29(5)：1-3，34.

Liu Xianlin，Chen Nan，Su Xiangjing，et al.Flexible power flow[J].Electric Power Automation Equipment，2009，29(5)：1-3，34.

[24]杭乃善，周航，李如琦.稳态控制潮流的设定空载频率及空载电压算法[J].中国电机工程学报，2003，23(12)：77-81.

Hang Naishan，Zhou Hang，Li Ruqi.Algorithm of setting open-circuit frequency and voltage for steady-state control power flow[J].Proceedings of the CSEE，2003，23(12)：77-81.

[25]王淳，程浩忠.基于模拟植物生长算法的配电网重构[J].中国电机工程学报，2007，27(19)：50-55.

Wang Chun，Cheng Haozhong.Reconfiguration of distribution network based on plant growth simulation algorithm[J].Proceedings of the CSEE，2007，27(19)：50-55.

[26]胡汉梅，郑红，李劲.基于模拟植物生长算法的配电网继电保护整定优化的研究[J].电力系统保护与控制，2012，40(7)：19-24.

Hu Hanmei，Zheng Hong，Li Jin.Research on the optimal coordination of the distributed networks relay protection based on the plant growth simulation algorithm[J].Power System Protection and Control，2012，40(7)：19-24.

[27]张健南，林涛，余光正，等.大规模电力系统阻尼控制器协调优化方法[J].电网技术，2014，9(9)：2466-2472.

Zhang Jiannan，Lin Tao，Yu Guangzheng，et al.Coordinated optimization of damping controllers in large-scale power system[J].Power System Technology，2014，9(9)：2466-2472.

[28]陈曦.基于风险理论的电力系统静态安全性评估方法研究[D].武汉：华中科技大学，2012.

[29]谢春瑰，方菲，吕项羽，等.电网脆弱性评估方法研究[J].电网与清洁能源，2013，29(5)：35-38.

Xie Chungui，Fang Fei，Lü Xiangyu，et al.Research on power grid vulnerability assessment methods[J].Power System and Clean Energy，2013，29(5)：35-38.

作者简介

毕如玉女，1991年生，博士研究生，研究方向为电力系统运行与控制。

E-mail：biruyu@sina.com

林涛男，1969年生，教授，博士生导师，研究方向为电力系统运行与控制、电力系统继电保护、新能源发电与智能电网、电能质量分析与控制。

E-mail：tlin@whu.edu.cn(通信作者)

The Security Correction Strategy in AC and DC Hybrid Power System

Bi Ruyu1Lin Tao1Chen Rusi1Xu Xialing2Ye Jing1

(1.School of Electrical EngineeringWuhan UniversityWuhan430072China 2.Central China Electric Power Dispatching and Communication CentreWuhan430077China)

AbstractWith the rapid development of AC-DC hybrid power system，the risk of cascading failures caused by DC block or line tripping is also increasing.Relevant control measures should be taken to avoid further overload according to the operation status of power grid.In smart grid，HVDC and thyristor controlled series capacitor (TCSC) can also be taken as control measures to further reduce the amount of load shedding.The sensitivity and optimization based methods are often utilized to formulate the security correction strategies.The sensitivity based method functions well in online generation rescheduling and load shedding.However，the power flow sensitivities of DC power and TCSC reactance are discovered to vary according to control variable rather than being constant.So it’s difficult for the sensitivity based method to be applied to security correction strategy of AC/DC hybrid power system.A modified optimization method，which uses heuristic search principle，is proposed against the defects of excessive optimization variables and heavy computational burden，which results in the limitation for online application.Based on load shift factor(LSF)，few generator and load nodes are rapidly selected to control overload effectively.Aiming at the minimum amount of load shedding，an optimization model is proposed，in which HVDC power and reactance of TCSC，in addition to the power of the selected nodes are taken as optimization variables.Intelligent optimization algorithm is adopted to obtain security correction scheme.Based on modified IEEE 30-node benchmark，the validity and superiority of the proposed method is verified by comparing the result obtained by the proposed method with those without utility of heuristic search or without taking DC power and TCSC reactance into consideration.

Keywords：Cascading failures，security correction，thyristor controlled series capacitor(TCSC)

中图分类号：TM73

国家自然科学基金面上资助项目(51177111)。

收稿日期2015-04-14改稿日期2015-06-01