① 模糊环境下几何平均亚式期权的保险精算定价
胡 攀,李爱民,唐海军
(四川文理学院数学与财经学院,四川达州635000)
①模糊环境下几何平均亚式期权的保险精算定价
胡攀,李爱民,唐海军
(四川文理学院数学与财经学院,四川达州635000)
摘要:在标的股票价格服从几何Liu过程的模型假设下,首先利用保险精算法给出几何平均亚式看涨、看跌期权的定价公式;其次,讨论了定价公式关于各参数的单调性和凹凸性; 最后,用所建模型计算煤层气开发项目的增长期权价值,为煤层气项目的价值评估提供了一种新的思路和方法.
关键词:模糊因素;保险精算法; 几何平均亚式期权
0引言
分数布朗运动作为自适应的高斯过程,是布朗运动的推广,由于其可以刻画长期相依性而在股票的价格模型中取代了布朗运动.但随着不确定性理论的发展,人们发现金融市场上除了存在随机性以外,还存在大量的模糊性.
为了处理模糊过程,1965年Zadeh用隶属函数引入了模糊集合的概念,[1]2002年Liu通过定义可信性测度和模糊事件的自对偶性,[2]建立起了可信性理论,使之成为研究模糊理论的一个数学分支,2008年在模糊环境下提出了与布朗运动相对应的Liu过程的概念用于描述动态模糊,Liu[3]同时建立了Liu股票价格模型.从此基于Liu股票价格模型的期权定价公式及其应用便开始发展起来.[4-7]然而上述模型并不能解决股价在短期内的异动对期权价值影响的问题,因此期权持有者可以通过短期内操纵股价来牟利,从而破坏金融市场次序.
亚式期权作为一种强路径依赖性期权,标的资产(如股票)的期末价值采用期权持有期内的平均值,从而可以有效避免股价的短期异动对期权价值的影响.亚式期权分为算术平均和几何平均两种.由于算术平均价格的精确分布并不存在,所以算术平均亚式期权的定价公式很难求得,而几何平均价格服从对数正态分布,因而几何平均亚式期权的定价公式比较容易求得.随机条件下亚式期权的定价公式是在放宽B-S模型的某些假设条件下得到的,如跳-扩散模型、[8]随机利率模型、[9]随机波动模型等.[10]由于现实的金融市场中存在大量的模糊性,因而考虑模糊环境下几何平均亚式期权的定价问题更符合实际的需要.
受上述研究的启发,本文在假设金融市场受模糊性因素影响的条件下,研究几何平均亚式看涨、看跌期权的定价问题.
1预备知识
1.1可信性理论
定义1[3]模糊过程Ct被称为是Liu过程,如果它满足(i) C0=0; (ii)Ct具有独立平稳增量; (iii) 任意增量Cs+t-Cs是均值为et,方差为σ2t2的正态分布模糊变量,其隶属函数为
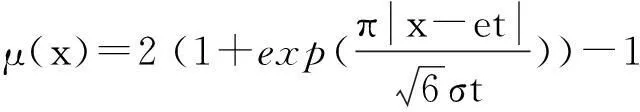
(1)
特别,当e=0,σ=1时称Ct为标准Liu过程.
定义2[3]假设Ct是一个标准Liu过程,称模糊过程Gt=exp(et+σCt)为几何Liu过程.


(2)
期望值为
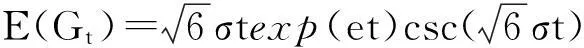
(3)

引理2[11]对任意t>0,It的正态隶属函数为
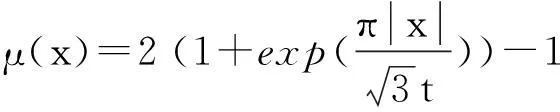
(4)
引理3[12](可信性反演定理) 假设ξ是隶属函数为μ的模糊变量,对于任意实数集合B,ξ的可信性测度

(5)
定义4[13]假设ξ是一个模糊变量,则ξ的期望值为

(6)
1.2Liu股价模型
假设模糊金融市场中仅存在两种证券:一种为债券,t时刻的价格记为Bt;另一种为股票,t时刻的价格记为Xt.文献[3]给出了股票价格的一般模型
(7)
1.3保险精算法
1998年,Bladt和Rydberg首次提出将期权定价转化为公平保费的保险精算计算问题.[14]2005年Norbet Schmitz用反例验证了在风险资产的收益率大于无风险利率的情况下,[15]若风险资产和无风险资产都按无风险利率折现,则市场存在明显的套利机会,进而提出了为期权定价时,风险资产按期望收益率折现,无风险资产应按无风险利率折现的改进的保险精算法.

2几何平均亚式期权定价公式


(8)
证明:



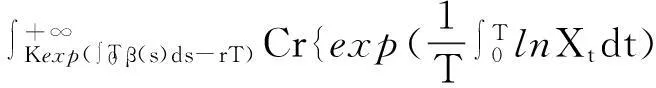



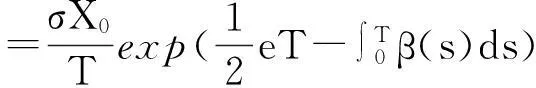
(9)
当u≥0时,由可信性反演定理可知

(10)
(11)
综合(10)(11)两式有
(12)
将(12)式代入(9)式即得结论.

(13)
证明:本定理的证明类似于定理2的证明.这里从略.
定理4几何平均亚式看涨期权的价格C=C(X0,K,e,σ,r)具有如下性质:
① C是X0的单调增加凸函数;
② C是K的单调减少凸函数;
③ C是e的单调减函数;
④ C是σ与r的单调增函数.
证明:① 本性质表明在其余参数不变的条件下,几何平均亚式看涨期权的价格C=C(X0,K,e,σ,r)是股票初始价格X0的单调增函数和凸函数.根据公式(7)有
于是,
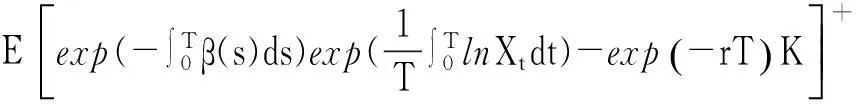





同理可得几何平均亚式看涨期权的价格C是无风险利率r的增函数.
定理5几何平均亚式看跌期权的价格P=P(X0,K,e,σ,r)具有如下性质:
① P是X0的单调减少凸函数;
② P是K的单调增加凸函数;
③ P是e的单调增函数;
④ P是σ与r的单调减函数.
证明:本定理的证明类似于定理4的证明过程,这里略.
3实例应用
煤层气俗称瓦斯,是一种非常规的天然气,其主要成分是甲烷.煤层气项目作为风险类项目之一,其投资开发是一项投资高、不可逆、极为复杂和大型的系统工程,现有的煤层气项目的价值评估主要采用的是折现值法(DFC法)、实物期权法和增长期权法.已有研究表明折现值法已很难准确评估风险类项目的价值;由于实物期权法所用数据信息的确定性,使得项目价值计算结果过于刚性化;[16-17]而增长期权法主要是将煤层气项目的价值看做项目本身价值加后续投资的增长期权的价值,增长期权主要采用的是基于B-S公式的价值评估方法.[18]煤层气主要赋存在煤层中,其开采往往伴随着煤炭资源的开发和能源利用,因此有关煤炭资源的开采就可看成是一个基于煤层气项目的增长期权.由于在某些时段内煤炭价格波动较为明显,如果直接采用B-S公式评估后续项目增长期权价值,可能会让煤层气开发企业做出错误决策并给其带来巨大损失和不良后果.于是在项目开发期内采用煤炭价格的几何均值来估算增长期权的价值更具有现实意义.
某企业获得某地区煤层气和煤炭项目的双料开采权,为了保障煤炭开采安全,该公司决定先进行煤层气开采,待煤层气开采结束后便进行煤炭资源开采.该地区拥有15亿m3煤层气,预计年产量3亿m3,可持续开采T=5年,煤层气当前立即投资开发的成本K=9亿元,煤层气项目年净现金流约为1.7亿元,财务基准收益率i=8%;煤炭开发项目总价值的现值为10亿元,后续投资成本为5亿元,无风险利率r=3.25%,煤炭项目的价值波动率σ=0.25,预期收益率e=12%.
3.1传统净现金流分析法
根据DCF计算方法,该煤层气项目的现值和净现值分别为

因为NPV<0,所以该煤层气项目应该不予投资.3.2利用B-S的看涨期权计算增长期权的方法
如果在项目持续期内煤炭价格相对平稳,则利用B-S公式计算增长期权的价值OP=8.2975亿元(模型参见文献[18]),则煤层气项目的价值P=NPV+OP=8.2975-2.2124=6.0851亿元.此时煤层气项目的价值P>0,所以该项目可进行投资.
3.3基于几何平均亚式看涨期权计算增长期权的方法
如果在项目持续期内煤炭价格波动频繁,则可利用模糊环境下几何平均亚式看涨期权的定价公式计算该煤层气项目的增长期权的价值OC=6.0380e-010,煤层气项目的价值P=NPV+OC=-2.2124 + 6.0380e-010亿元.显然P<0,即该项目不应该进行投资.
按照折现值法和模糊几何平均亚式期权定价模型计算煤层气项目的价值均为负,说明应持续等待或放弃投资,而基于B-S公式的价值评估方法得到的项目价值为正,可以立即开发.
4小结
在充分考虑了模糊性因素的影响后,给出了模糊环境下几何平均亚式期权的价值计算公式,增强了期权定价的科学性和合理性.将所建模型用于煤层气项目的价值评估,并将计算结果与用DCF法和B-S模型计算的结果作比较,提出可根据煤层气项目后续投资项目资产价格变化的具体情况选择不同的模型评估煤层气项目的价值.
参考文献:
[1]Zadeh L A.Fuzzy sets[J].Information and Control,1965(8):338-353.
[2]Liu BD.Foundation of Uncertainty theory[M].Beijing:Tsinghua University,2006:81-96.
[3]Liu B.Fuzzy process , hybrid process and uncertain process[J].Journal of Uncertain Systems,2008(1):3-16.
[4]Qin ZF,Li X.Option pricing formula for Fuzzy financial market[J].Journal of Uncertain Systems,2008(1):17-21.
[5]谭英双.基于模糊不确定环境的高新技术项目价值评估模型[J].系统工程理论与实践,2010(6):1021-1026.
[6]Qin Z F,Gao X.Fractional Liu process with application to finance[J].Mathematical and Computer Modeling,2009,50(9/10):1538-1543.
[7]胡华.标的股票服从几何分数Liu过程的幂期权定价模型[J].河南师范大学学报:自然科学版,2013(2):1-5.
[8]Wang K,KimiI K,Qian X S.Convergence of the binomial tree method for Asian options in jump-duffision models[J].Mathematical analysis and applications,2007(1):10-23.
[9]王莉君,张曙光.Vasicek利率模型下的亚式期权的定价问题和数值分析[J].应用数学,2003(3):467-474.
[10]Wong,Cheng.GeometricAsian options:Valuation and calibration with stochastic volatility[J].Quantitative Finance,2004(4):301-314.
[11]Qin ZF,Li X.Fuzzy calculus for finance[M].Beijing:Tsinghai University,2008:1-54.
[12]Liu B.Uncertainty theory[M].Berlin:Springer-Verlag,2007.
[13]Liu B,Liu YK.Expected value of fuzzy variable and fuzzy expected value models[J].IEEE Transactions on fuzzy Systems,2002(4):445-450.
[14]Bladt M,Rydberg HT.An actuarial approach to option pricing under the physical measure and without marketassumptions[J].Insurance:Mathematics and economics,1998(1):65-73.
[15]Norbert S.Note on option pricing by actuarial considerations[J].Insurance:Mathematics and Economics,1998(1):65-73.
[16]许晓东,张丽英,杨玉凤,等.实物期权模型在煤层气项目评价中的应用[J].中国煤炭,2011(6):27-30.
[17]张胜有,冯立杰,魏红,等.基于实物期权方法的煤层气项目延迟投资决策研究[J].工业技术经济,2009(8):77-79.
[18]冯立杰,翟雪琪,王金凤,等.基于增长期权的煤层气开发项目价值评估模型[J].价值工程,2011(5):14-15.
[责任编辑范藻]
The Actuarial Pricing of Geometric Average Asian Options under Fuzzy Environment
HU Pan,LI Aimin,TANG Haijun
(Mathematics and Finance-Economics School of Sichuan University of Arts and Sciences,Dazhou Sichuan 635000,China)
Abstract:In the process of the underlying stock price follows geometric Liu model assumptions,the geometric average Asian call and put options pricing formula are given by using of actuarial method; Secondly,the monotonicity and convex-concave of the parameters in the model are discussed; Finally,the growth option value of CBM development project is calculated by using the model,it provides a new thought and method for the value of CBM project assessment.
Key words:fuzzy factors; actuarial pricing method; the geometric average Asian options
收稿日期:2015-11-18
基金项目:①四川省教育厅2016年度一般项目“基于模糊理论的煤炭项目价值评估与投资决策分析”(16ZB0354);四川文理学院2014年度面上项目“模糊环境下煤层气项目的价值评估与最佳投资决策研究” (2014Z009Y)
作者简介:胡攀(1983—),男,四川雅安人.讲师,硕士,主要从事金融数学与灰色系统理论研究.
中图分类号:F830.9
文献标志码:A
文章编号:1674-5248(2016)02-0007-05

