基于混沌信号序列的数字信封

杨晓云，徐强，庄燕滨

(常州工学院计算机信息工程学院，江苏常州213002)



基于混沌信号序列的数字信封

杨晓云，徐强，庄燕滨

(常州工学院计算机信息工程学院，江苏常州213002)

摘要：讨论了混沌信号序列为序列密钥的特点，综合利用公开密钥技术的灵活性和对称密钥技术加密、解密速度快、实时性好的优点，提出了一种以混沌信号序列为密钥的数字信封技术，并详述了采用ARM来完成一种数字信封的硬件实验方案。

关键词：混沌信号；序列密码；数字信封；ARM

0引言

序列密码(又称对称密钥技术)是密码学中一个重要的信息加密系统[1]，其特点是加密与解密使用同一密钥。序列密码不存在数据扩展，实时性好，硬件容易实现，但是要便捷地将发送端密钥信息递送给接收端，而且要保密，这就是需要进一步探讨的问题。

数字信封(又称电子信封)技术解决了这个问题，图1为其原理图[2]。数字信封工作原理是：发端用公开密钥(KU)对序列密钥的序号加密并将其传输到收端，同时将明文经序列密钥加密成的密文，亦传送到收端；收端用自己的私钥(KR)解密出密钥序号并找到对应的序列密钥，而后用这序列密钥解密出明文来。

可见，数字信封技术综合利用了公开密钥的方便与灵活性和序列密码的安全与高效性。

1混沌序列密码系统

密钥序列是序列密码安全保密性的关键。通常希望密钥序列长度越长越好，同时又要求硬件实现方便。例如，目前常采用的M序列(伪随机序列之一)[3]，可由1个n级移位寄存器来构成1个周期为2n的二元序列。这个n级M序列的总数为

Mn=2(2n-1-n)

(1)

由式(1)可见，M序列的数量随移位寄存器级数n增加而急剧增大。因此，产生的密钥数量可以很大，硬件实现亦方便。由于现在计算机运算速度越来越快，特别是云计算，因此用M序列为密钥的加密系统，也较易被破译。

混沌是指确定性系统中产生貌似随机的不规则运动[4-7]。混沌信号具有非周期及良好的类随机噪声的特性，且产生混沌信号的系统对初始值具有高度的敏感性。因此，混沌序列具有无限长度，产生的序列密钥数量巨大，种类繁多，以混沌序列为密钥的序列密码系统很难被破译。图2为以混沌信号为密钥的序列密码系统原理图。该系统发端由明文序列与混沌序列密钥经模2加形成密文序列，经信道送到收端，收端用与发端相同的混沌序列密钥与密文序列进行模2加，即可得到与发端相同的明文序列。

2数字信封实验系统

本方案的数字信封实验系统原理图见图3，实验系统由发端时钟统一控制下进行工作。发端与收端均采用STM32F103VE16来实现，此芯片使用高性能的ARM@Cortex-M3 32位RISC内核，内置高达512 kB的闪存。STM32控制器自带RC振荡源，可以直接作为系统时钟，但精度不高。本系统对定时系统要求比较高，所以系统时钟采用外接8 MHz的时钟源，如图4所示。

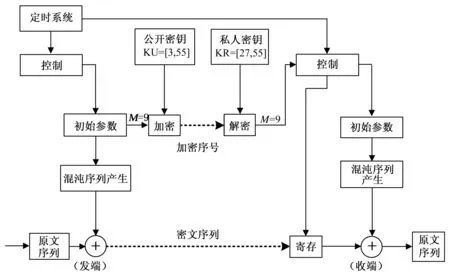
图3　数字信封实验系统原理图

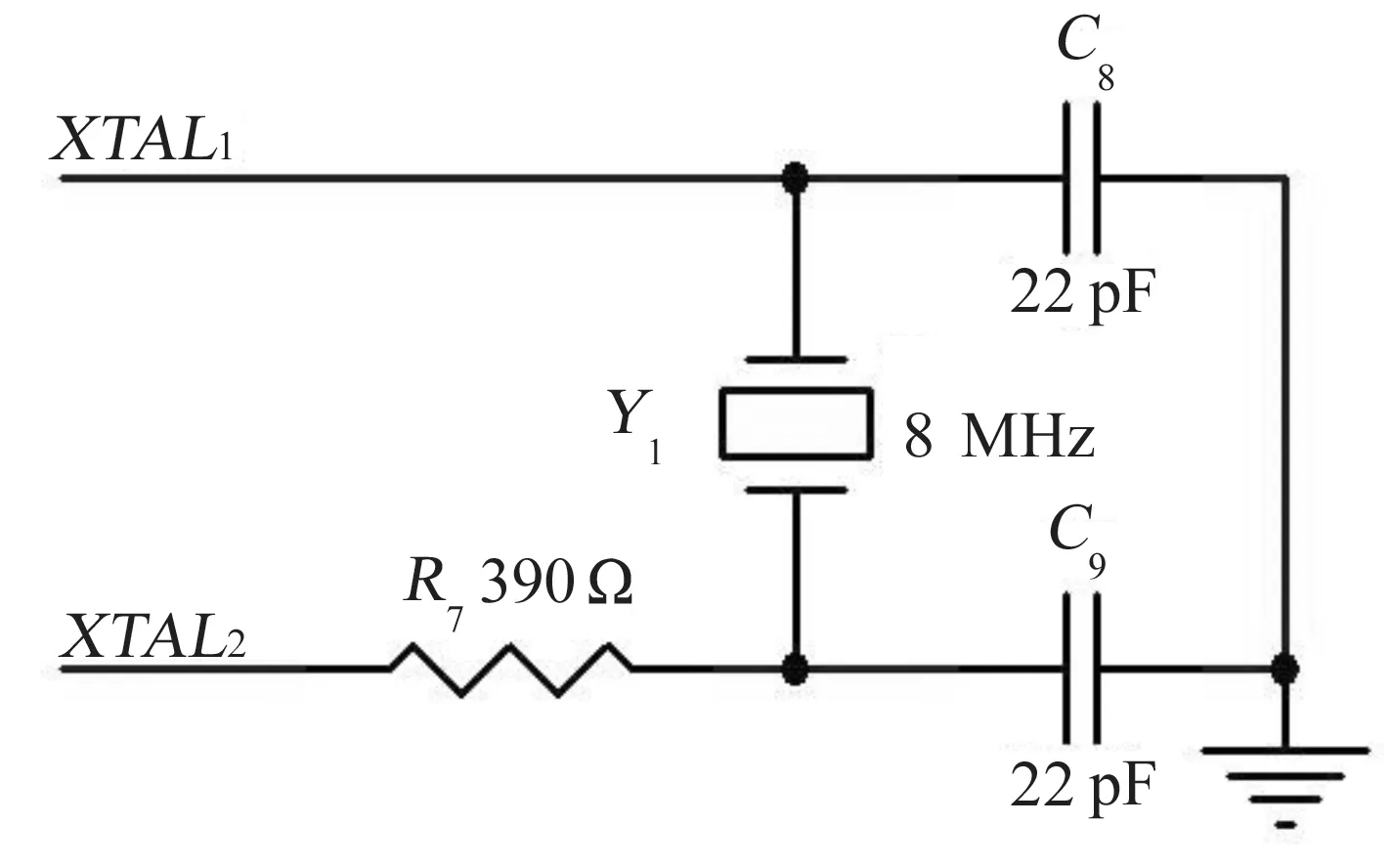
图4　系统时钟原理图

2.1混沌信号序列的产生[8-9]

本方案最关键的是由STM32F103VE16芯片来产生混沌信号序列，具体方法如下说明。

选用Lorenz系统的混沌电路，其一般数学形式为

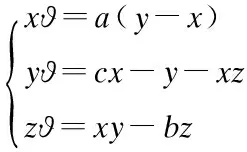
(2)

基于上述公式，采用简单的欧拉算法离散化，导出Lorenz系统离散迭代模型，并选择无量纲参数a=10，b=8/3，c=28，选择迭代步长h=0.001和初始值(x0,y0,z0)=(1,1,1)，用C语言设计基于芯片STM32F103VE16的运行程序进行运算，其程序流程如图5所示。

运算后产生了x/y/z三维混沌数据，每维可产生大量数据。仅选取x维前4个数据作为本方案密钥源，其十进制序列为(1.000 000，1.000 170，1.000 507，1.001 010)，将其转换成双精度浮点数。

浮点数运算模块的设计，所依据的标准为IEEE-754浮点数标准格式，它是国际电工电子学会在1985年制定的浮点标准格式，其中的双精度格式由1位符号位、11位阶码、52位尾位组成，共64bit。因此，作为本方案的混沌序列密钥源为(3FF0000000000000，3FF000B242070B8D，3FF00213A0C6B485，3FF004230FCF80DC)，密钥源长度为256 bit，密钥比特流之间没有任何相关性。本方案的收发二端均用此混沌信号序列，并设步长h=0.001，初始条件(x0,y0,z0)=(1,1,1),序号M=9。只要改变步长、初始条件等参数，可得到不同密钥长度序列信号，并对应不同的序号。规定用不同序号来告知收端，本次传送的原文是使用哪个混沌密钥序列进行加密的。收端便可按规定的方法，找到对应的混沌密钥序列的初始参数产生密钥序列。

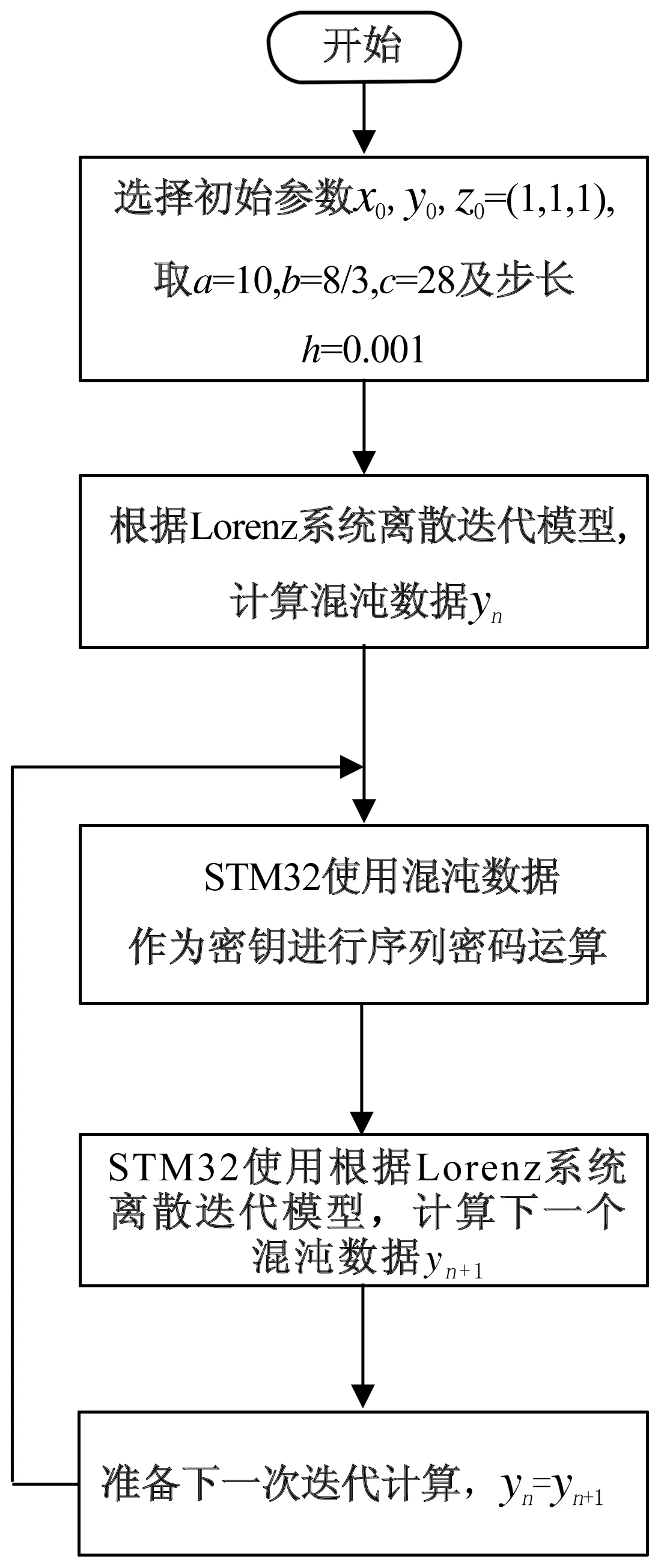
图5　混沌密码程序流程图

2.2公开密钥密码的产生

公开密钥简称公钥(KU)是代表与收端人的地址、网址、电话号码等一样的公开信息。若要向收端发送加密信息，就可用公钥加密后送给收端。收端可用私人密钥(KR)将其解开，别人通常无法解开。本方案是采用RSA算法，得到公钥(KU)与私钥(KR)的具体算法如下：

① 选2个素数p和q(如p=5,q=11)；

② 计算n=pq(如n=5×11=55)；

③ 计算Φ(n)=(p-1)(q-1)(如Φ(n)=4×10=40)；

④ 选e，e<Φ(n)，并与Φ(n)互素(如取e=3)；

⑤ 求d，de=1modΦ(n)且d<Φ(n)(得到d=27)。

这样便可得到KU=[e,n]，KR=[d,n]，本方案中KU=[3,55]，KR=[27,55]。

2.3数字信封实验方案的实现

发端首先将本方案规定的序号M=9(代表产生混沌序列的初始参数)，用公钥KU=[e,n]=[3,55]进行加密，序号密文为C=Memodn=(9)3mod55=14，将此序号密文送到收端。本方案采用1个与混沌密钥序列等长度的测试序列为原文序列(FFFF0000FFFF0000，F0F0F0F0F0F0F0F0，33333

33377777777，5555555555555555)。

发端要将此原文序列与本次采用的混沌序列密钥信号进行模2加，形成密文序列送到收端去。

图6是利用C语言根据上述加密方法为STM32F103VE16芯片编写的程序流程图。

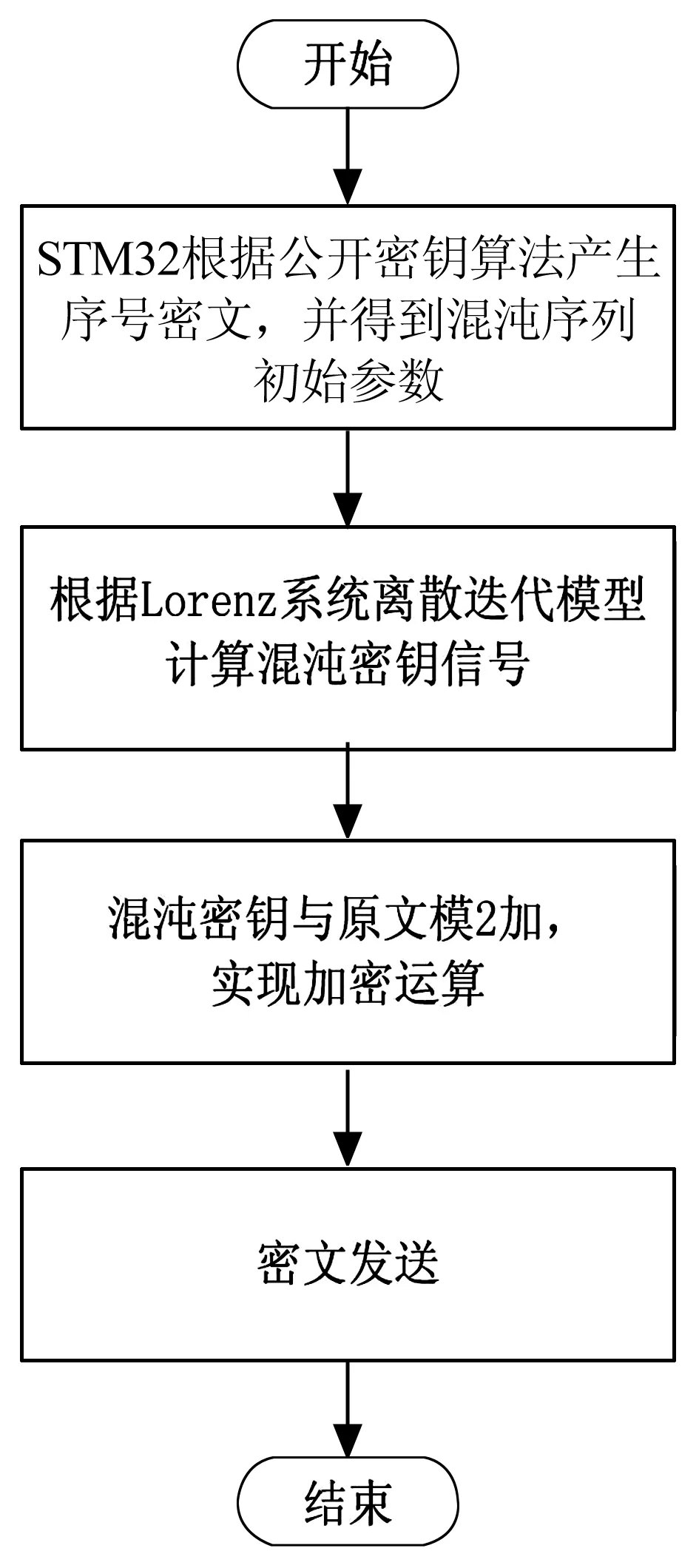
图6　数字信封发端程序流程图

收端要另用1个独立的STM32F103VE16芯片。在系统的统一时钟控制下，首先用私钥，按如下方式解密出序号：

M=Cdmodn=(14)27mod55=9

收端控制系统将对应M=9的混沌序列产生初始条件(x0,y0,z0)=(1,1,1)和迭代步长h=0.001送给本地混沌序列产生器，得到与发端相同的混沌密钥序列。在控制系统同步控制下，将寄存器中的密文序列与本地产生的混沌密钥序列进行模2加，便可得到原文序列。

用C语言将上述运算及各种处理对芯片STM32F103VE16进行编程，图7为数学信封收端程序流程图。

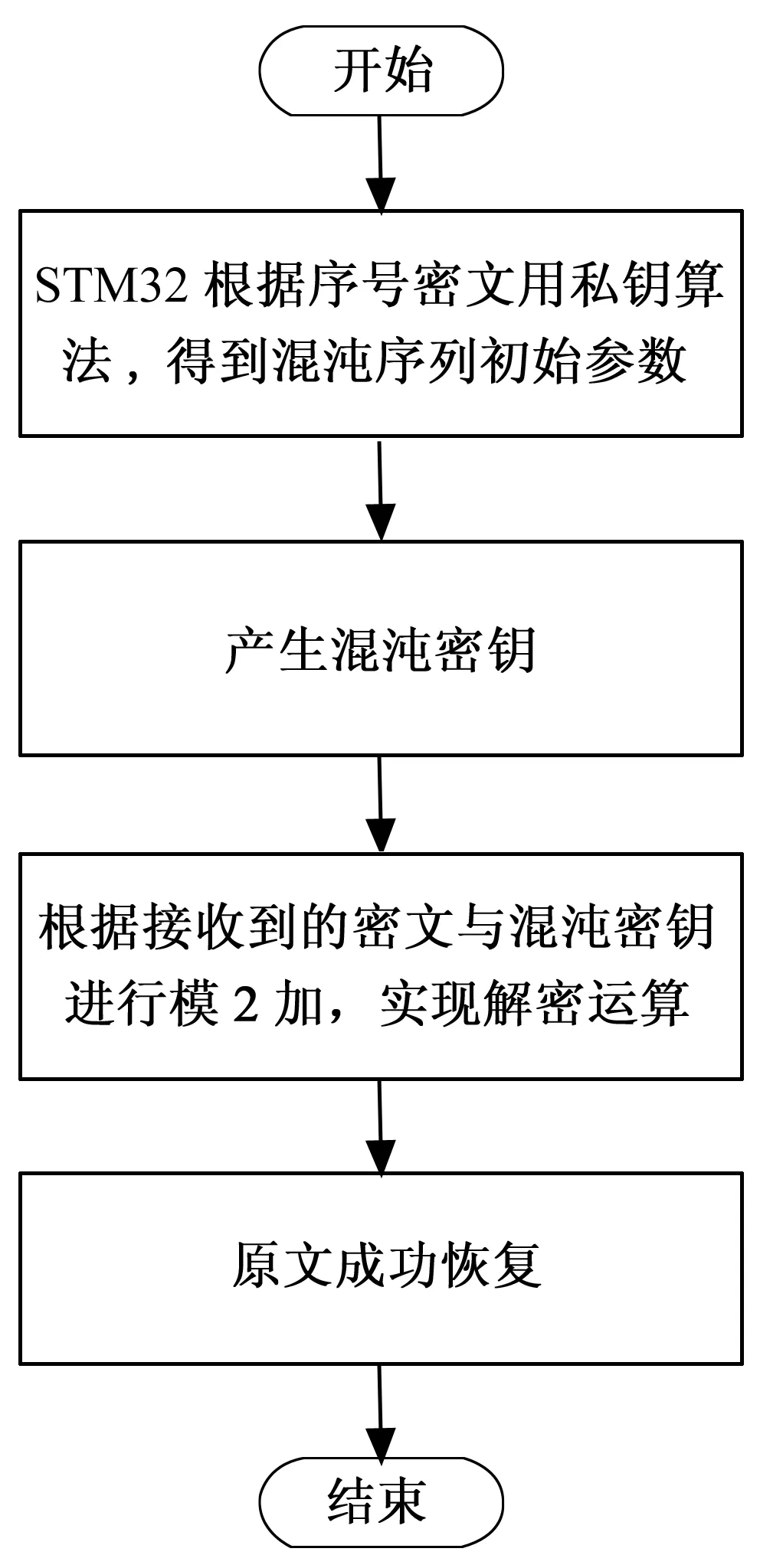
图7　数字信封收端程序流程图

3结语

经实验测试,基于ARM的数字信封实验方案是可行的，但离验证和实际应用还有不少技术难点，硬件实现比较复杂，尤其是混沌同步。随着数字信号器件与处理技术的发展，这些问题将逐步得到解决。

随着“互联网+”和电子商务的飞速发展，网络信息安全越来越重要。为了保证信息在网络传输过程中不被非法窃取、篡改，必须对发送的信息进行加密。基于混沌信号序列的数字信封技术是一种很好的加密方法。该方法外层用公开密钥技术，方便灵活地将混沌序列密钥相应的序号送给收端；收端根据序号用相应的初始值和步长产生真正的密钥，才能正确解密。同时，由于混沌信号具有非周期性、宽频带功率谱、类随机噪声的特性，具有长期不可预测的特点，攻击者很难对其进行跟踪、分析、破解，故这种方法的信息传输保密性是非常好的。因此，基于混沌信号序列的数字信封技术是非常具有应用价值的。

[参考文献]

[1]WILLIAM S.密码编码学与网络安全：原理与实践[M].5版.王张宜，译.北京：电子工业出版社，2011.

[2]仝新顺.电子商务概论[M].北京：人民邮电出版社，2015.

[3]陈智雄.伪随机序列的设计及其密码学应用[M].厦门：厦门大学出版社，2011.

[4]李辉.混沌数字通信[M].北京：清华大学出版社，2006.

[5]关新平，范正平，陈彩莲，等.混沌控制机器在保密通信中的应用[M].北京：国防工业出版社，2002.

[6]方锦清.混沌通信及其相关网路信息安全研究的若干进展[J].系统工程学报，2010，25(6)：725-741.

[7]杨晓云，徐强，庄燕滨.混沌在序列密码系统中的应用[J].常州工学院学报，2013，26(8)：43-45.

[8]徐强，包博成，胡文，等.数字实现混沌系统的建模、仿真与实验[J].计算机工程与设计，2010，31(15)：3404-3407.

[9]徐强，包博成，杨晓云.蔡氏电路方程的离散化与数字电路实现[J].计算机应用研究，2011，28(6)：2158-2160.

责任编辑：陈亮

Digital Envelope Based on Chaos Signal Series

YANG Xiaoyun，XU Qiang，ZHUANG Yanbin

(School of Computer Information & Engineering,Changzhou Institute of Technology,Changzhou 213002)

Abstract：The characteristics of chaotic signal sequences as a sequence key are discussed.This paper proposes a digital envelope technology based on the key of a train of chaos signals which fully takes the advantages of the flexibility of the public key technology and the high-speed and real-time features of the symmetric key for encryption and decryption.A hardware experimental scheme of the digital envelope is presented by using ARM.

Key words：chaos signal;stream cipher;digital envelope;ARM

doi:10.3969/j.issn.1671- 0436.2016.02.011

收稿日期：2016- 01- 05

作者简介：杨晓云(1970—)，女，实验师。

中图分类号：TN918

文献标志码：A

文章编号：1671- 0436(2016)02- 0047- 04