基于改进布谷鸟搜索算法的图像分割
李瑞芳
(西安电子科技大学 数学与统计学院,陕西 西安 710126)
基于改进布谷鸟搜索算法的图像分割
李瑞芳
(西安电子科技大学 数学与统计学院,陕西 西安710126)
摘要针对布谷鸟搜索算法在应用其进行图像分割时计算量大、易陷入局部极小值解、收敛速度慢的问题。文中采用一种基于改进布谷鸟搜索算法的多阈值图像分割算法。该算法以Ostu算法设计自适应度函数,将布谷鸟搜索算法和K均值算法融合,增加种群的多样性,且能自适应地确定阈值个数及其范围,并找到待分割图像的最优阈值。实验结果表明,与K均值算法和布谷鸟搜索算法相比,该算法找到的阈值质量更佳,图像分割结果更好。
关键词图像分割;阈值分割;K均值
图像分割的核心思想是通过采取一定的技术手段提取目标区域,是图像分析之前的必要准备。分割图像的方法有多种,其中最经典的当属大津算法,即Ostu法[1]及其各种改进方法[3-4]。基于聚类分析的图像分割方法也是较为常见的图像分割方法,K均值算法便是其中一种。利用K均值算法做图像分割实质上就是以反复迭代的方法对图像像素点进行划分分类,求得一个较好的像素分组。K均值算法因其算法简单、收敛速度较快等优势,在图像处理领域得到了广泛应用[5-6]。
近年来,随着生物启发式算法的迅速发展,研究者们也顺势将这些启发式算法成功应用于图像处理领域,如布谷鸟搜索算法(CS)[2]便可应用于图像分割。文献[2]表明在多峰值优化问题中,CS算法要比PS0算法、GA算法的稳定性和遗传性要好,且CS算法结构简单、参数少。但CS算法也存在收敛速度慢、搜索精度低、易陷入局部极小值点等不足。Walton等人建议使用随代数递减的步长因子来加速算法的收敛速度[7],Valian等人提出自适应步长和自适应发现概率的自适应CS算法[8]。此外,还有诸多学者对CS算法进行研究[9-11],但CS算法所固有的缺点仍未得到较好地克服。为充分利用K均值算法和CS算优势的同时克服其不足之处,本文提出一种修正的CS算法(MCS)。
1算法的原理
由于本文所提出的算法是基于阈值的图像分割,故选Ostu法,即类间方差(1)作为适应度函数
(1)
1.1确定阈值个数和范围
首先利用自适应K均值算法[12]确定某个鸟巢
xI=(x1,x2,…,xM)
(2)
其中,m表示每个鸟巢中鸟蛋的数量,即优化问题中解空间的维数。在灰度图像中,灰度值[0,L-1]便是鸟巢位置,故m=1。
然后根据Xi的取值确定阈值范围
Ub=Xi+[diff(Xi),0],Ub(n)=L-1
(3)
Lb=Xi-[diff(Xi),0],Lb(1)=0
(4)
其中,diff(Xi)=[x2-x1,…,xn-xn-1]。
最后初始化鸟巢
X=(X1,X2,…,Xn)=Lb+rand×(Ub-Lb)
(5)
其中,rand∈[0,1]。
1.2修正的CS算法(MCS)
由于CS算法属于启发式算法,故其固有的后期收敛速度慢、易陷入局部极小的缺点仍然存在。鉴于此,本文提出一种修正的CS算法(MCS),即在CS算法中引入k均值聚类算。MCS算法的基本思想:经过改进后的鸟巢位置X(t+1)不会直接进入下一次迭代,而是对其做k均值聚类,产生一个较好的鸟巢位置,并与当前最佳的鸟巢位置作比较并保留质量较好的鸟巢位置,然后再进入下一次迭代,继续利用CS算法计算。如此便使得种群多样性增加,走出了易陷入局部最优解的困境取得全局最优解,且收敛速度和搜索精度在一定程度上也有所提高。修正布谷鸟搜索算法,即MCS:
步骤1初始化MCS算法的鸟巢。运用上述方法初始化鸟巢x=(x1,x2,…,xn),xI=(x1,x2,…,xM)其中,n表示鸟巢数量,M表示每个鸟巢中鸟蛋数量,即优化问题中解空间的维数;
步骤2根据适应度函数计算初始化的鸟巢质量;
步骤3各鸟巢主人使用Levy飞行机制更新自己的鸟巢位置。根据适应度函数计算更新后的鸟巢质量,并与更新前的鸟巢质量作比较,利用贪婪算法保留质量较好的鸟巢位置。鸟巢位置的更新公式为
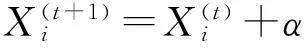
(6)
其中,t表示迭代次数;α~N(0,1)表示步长控制;⊕表示点乘运算符;S表示Levy搜索路径,即步长
(7)
步骤4按发现概率Pa丢弃质量较差的鸟巢,并用随机游动机制产生新的鸟巢来代替丢弃的鸟巢
(8)
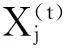
步骤5对改进后的鸟巢做k均值聚类,产生一个较好的鸟巢位置;
步骤6将步骤5中所得求鸟巢质量与当前质量最佳的鸟巢位置作比较,保留质量较好的鸟巢位置,并根据式(3)和式(4)更新鸟巢位置范围,最后根据式(5)更新鸟巢;
步骤7当达到最大迭代次数就终止迭代计算,输出质量最好的鸟巢,否则返回步骤2~步骤5。
2算法的流程
MCS算法如下:输入:图像u,发现概率Pa,迭代次数t,鸟巢数目n。输出:分割图像u1。
步骤1利用自适应快速k均值算法[12]求得初始阈值,确定分割阈值个数num及其范围Ub,Lb;
步骤2计算各个灰度水平的像素点数目、概率及期望;
步骤3随机初始化各个鸟巢的位置,并计算适应度;
步骤4将发现概率Pa与Pa∈[0,1]比较,根据比较结果更新鸟巢位置;
步骤5计算更新后各个鸟巢的适应度,并与未更新前相对应的鸟巢的适应度做比较若结果较好,则用更新后的适应度替换更新前的适应度,并替换对应的鸟巢位置;
步骤6对比步骤5中所得的最新鸟巢位置的适应度,确定当前最优的鸟巢位置,即适应度最大;
步骤7利用k均值算法,对更新后的鸟巢进行聚类划分,求得一个质量较好的鸟巢,并与当前最优的鸟巢比较,保留较好的鸟巢及其适应度,并计算新的阈值范围Ub,Lb;
步骤8判断是否达到最大迭代次数,若达到最大迭代次数是则停止,否则返回步骤2;
步骤9利用所求得的最佳鸟巢,计算分割图像u1,并输出。
3算法的实验结果与分析
为验证本文所提图像分割算法的有效性,本文做了大量的实验仿真,并选择Peppers(256×256)、Livers(256×256)、Zebra(250×167)进行说明。新算法与k-means算法、CS算法的有效性用最大类间方差进行比较。对k-means模型和MC算法,严格按照其应用于图像分割的方法进行实验。设置发现概率Pa=0.25,鸟巢数目n=25,迭代次数t=500。
观察图1,发现图1(D)的对比度高于图1(b)和图1(c),所以分割效果较佳。
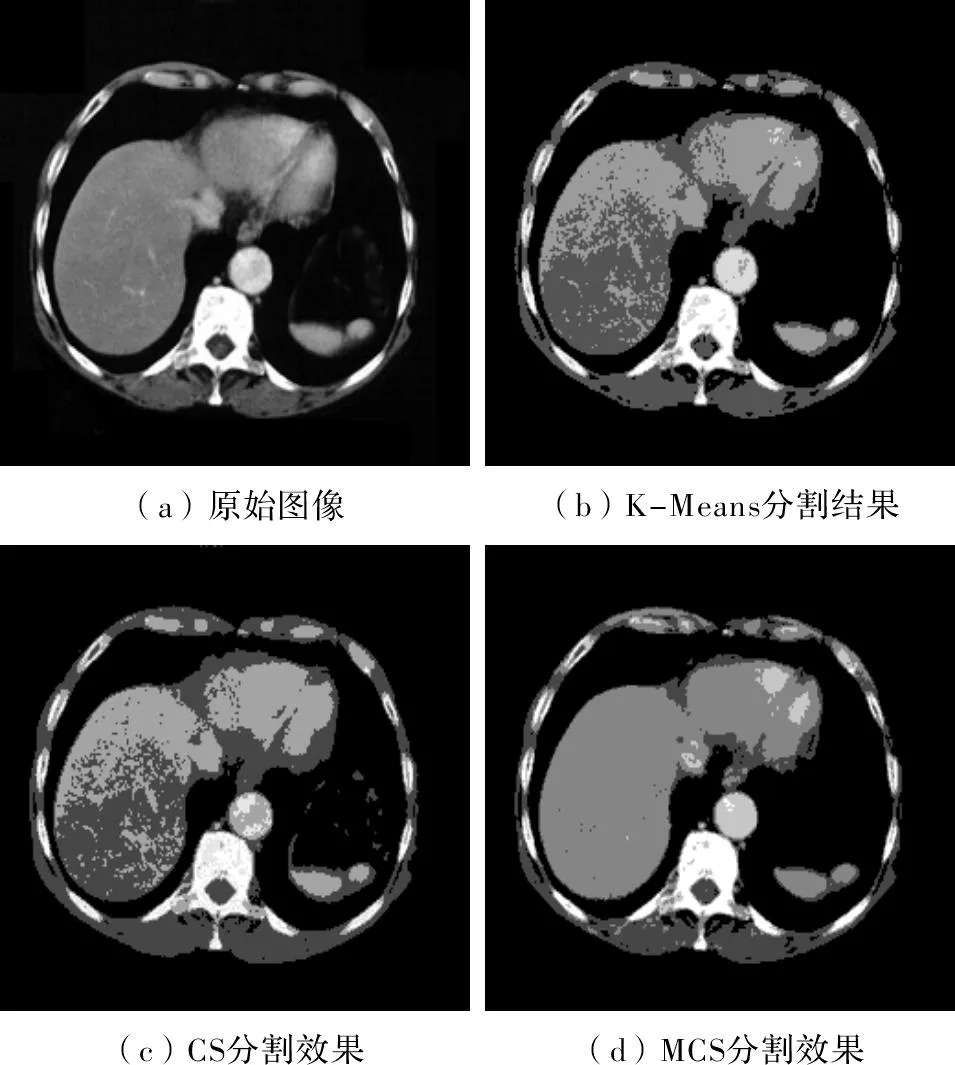
图1 Livers的分割结果
不同图像分割方法的最大类间方差和最佳阈值如表1~表3所示。从表中可知,相对于K-Means算法、CS算法,本文提出的图像分割算法(MCS)的最大类间方差值有明显增大。且CS算法和本文算法在相同的迭代你次数下,MCS算法的最大类间方差大于CS算法的类间方差,这说明MCS算法的收敛速度要比CS的收敛速度快。同时,MCS算法阈值个数及其初始值的确定是自适应的,而CS算法、K-Means算法阈值个数及其初始值的确定是需不断调整。所以,从时间成本来看,MCS算法也优于CS算法和K-Means算法。为对比这3种算法的分割效果,文中将CS算法和K-Means算法的阈值个数取为MCS算法所求得的阈值个数。

表1 对Peppers不同分割方法的阈值和最大类间方差
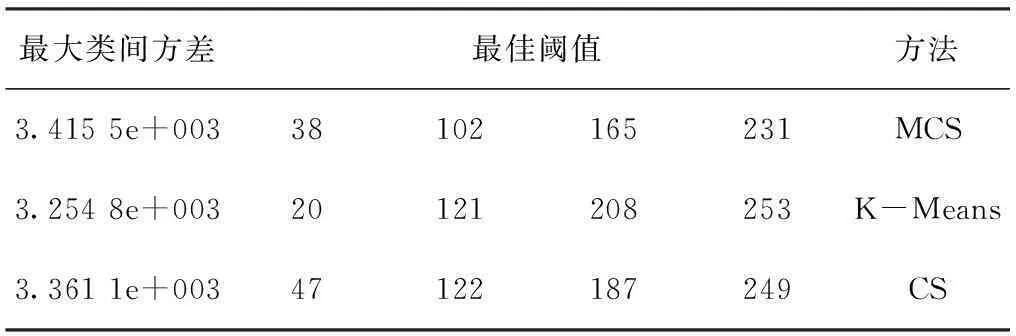
表2 对Livers不同分割方法的阈值和最大类间方差

表3 对Zebra不同分割方法的阈值和最大类间方差
4结束语
布谷鸟算法(CS)是受自然界中布谷鸟繁衍后代的特性激发,融入Levy飞行机制,从而形成了一种求解最优问题的方法。本文将布谷鸟算法和K均值算法融合,用于增强种群的多样性,以提高CS算法的搜索能力,走出了易陷入局部最优解的困境,且收敛速度在一定程度上也有所提高。此外,本文算法对阈值个数及其初始值的确定是自适应的,无需经过额外的调整。
参考文献
[1]Ostu N A.Threshold selection method from gray level histograms[J].IEEE Transactions on System,Man,and Cybernetics,1979,9(1):62-66.
[2]Yang Xingshe,Deb S.Cuckoo search via levy flights[C].Coimbatore,India:Proceeding of World Congress on Nature & Biologically Inspired Computing,2009.
[3]胡斌,宫宁生.一种改进的Otsu阈值分割算法[J].微电子学与计算机,2009,26(12):153-155.
[4]Liu Jianzhuang,Li Wenqing.Automatic thresholding using the otsu algorithm based on the two-dimensional gray image[J].Acta Automatica Sinica,1993,19(1):101-105.
[5]Pei Zhenkui,Hua Xia.The clustering algorithm based on particle swarm optimization algorithm[C].Hunan:International Conference on Intelligent Computation Technology and Automation,2008.
[6]Liu Jingming,Han Lichuan.Cluster analysis based on particle swarm optimization algorithm[J].Systems Engineering-Theory & Practice,2005(6):54-58.
[7]Walton S,Hassan O,Morgan K,et al.Modified cuckoo search:A new gradient free optimisation algorithm[J].Chaos Solitons & Fractals,2011,44(9):710-718.
[8]Valian E,Mohanna S,Tavakoli S.Improved cuckoo search algorithm for feedforward neural network training[J].International Journal of Artificial Intelligence & Applications,2011,2(3):36-43.
[9]Tawfik A S,Badr A A,Abdel-Rahman I F.One rank cuckoo search[J].International Journal of Computer Applications,2013,64(6):30-37.
[10]Long Wen,Chen Le.Hybrid cuckoo search algorithm for solving constrained chemical engineering optimization problems[J].Journal of Computer Applications,2014,34(2):523-527.
[11]Yang Xinshe,Suash Deb.Multiobjective cuckoo search for design optimization[J].Computers & Operations Research,2013,40(6):1616-1624.
[12]李玉鑑.自适应K-均值聚类算法[J].计算机研究与发展,2007(z2):100-104.
An Image Segmentation Algorithm Based on Modified Cuckoo Search
LI Ruifang
(School of Mathematics and Statistics,Xidian University,Xi’an 710126,China)
AbstractThe cuckoo search algorithm (CS) is a bionic algorithm,but its application to image segmentation suffers from such drawbacks as large amount of calculation,appearing local minimum and slow convergence.In order to solve these problems,we propose a multi-threshold image segmentation algorithm based on modified cuckoo search algorithm.This algorithm employs the Otsu method as the fitness function,combines the cuckoo search algorithm with the K-means algorithm for better diversity of population,and adaptively determines the number and range of the thresholds to find the optimal thresholds of the image to be segmented.Experimental results show that the MCS algorithm outperforms the K-means and the cuckoo search (CS) in terms of segmentation thresholds and segmentation effect.
Keywordsimage segmentation;threshold segmentation;K-means
doi:10.16180/j.cnki.issn1007-7820.2016.05.028
收稿日期:2015-10-17
作者简介:李瑞芳(1990—),女,硕士研究生。研究方向:多尺度分析理论及其在图像处理中的应用。
中图分类号TP391.41
文献标识码A
文章编号1007-7820(2016)05-105-03

