2015年“股灾”前后上证指数非对称性研究
孙世楠+周博文

[摘要]2015年6月末,中国股市在持续了一年多的高涨之后遭到重挫,出现了“股灾”,虽然政府积极应对,但市场情绪并未好转,恐慌继续蔓延,导致股市持续低迷。文章以“清配”和“停止托市”两个时间节点界定第一轮股灾,并运用TARCH模型和弹簧振子理论分析了上证指数在本轮股灾前后特征的变化。结果显示:上证指数在“股灾”后表现出显著的非对称性特征,并且“股灾”后上海股市反而有更高的配置效率和更低的市场摩擦。
[关键词]股灾;非对称性; TARCH模型;弹簧振子理论
1引言
在金融波动性研究领域中,很多专家学者通过GARCH族模型的应用比较深入地讨论了国内外股票市场的非对称性问题,然而在这些分析中却鲜有涉及市场效率的分析,这主要是受限于当前主流的随机游走模型的影响。
本文在运用常用的TARCH模型分析上证指数非对称性的同时引入弹簧振子理论。希望在描述上证指数的非对称性的同时可以通过弹簧振子理论计算市场有效性的相关指标,以更好地描述市场的运行状态。
2文献综述
GARCH族模型在研究市场波动性和非对称性方面有很好的效果,很多专家学者通过各自的研究得出了非常有用的结论。何晓光和朱永军(2007)运用ARMA-EGARCH及ARMA-TARCH模型,研究1993年1月以来沪深两市的A股指数的日收益数据,认为中国股票市场在发展的早期,市场表现为反向的非对称性或非对称不明显,而随着时间的发展,股市收益的波动则显现出带杠杆效应非对称性,即收益率波动的非对称性都表现出阶段性特征。方璐(2010)应用非对称的ARCH模型,研究金融危机前后我国上证A股指数,得出金融危机发生前“利好”对股指的冲击大于“利空”,危机发生后“利空”对股指的冲击大于“利好”的结论,即金融危机前后我国上证A股表现出了明显的非对称性。马鑫杰(2013)利用非对称的ARCH模型从牛、熊市两个时期分别比较利好与利空信息对股市冲击的程度,得出我国股票市场的有效性受不同周期信息不对称的影响的结论。
然而,另一些学者却得出了不同的结论。张虎和鲁鸽(2013)利用非对称的ARCH模型对上证指数和香港恒生指数进行实证研究和对比,发现上证指数不存在明显的波动不对称性,而恒生指数存在明显的波动不对称性,利空消息的作用大于利好消息的作用。林德钦(2014)运用GARCH族各模型对创业板指波动率的实证分析,发现AR(1)-GARCH(1,1)模型对创业板指波动率的预测更为有效。这表明,在创业板指数中,信息冲击的非对称效应并不明显。
此外,本文用到的弹簧振子理论,由赵贞玉等于2007年提出,该理论克服了有效市场假说中的“资本市场在新信息公布的瞬间完成了对该信息的反应并达到新的均衡”假设,统一了市场处于平稳期和对新信息进行反应的调整期的价格波动方程,并提供了衡量市场效率和摩擦的指标。
3模型介绍
3.1弹簧振子理论
弹簧振子理论的基本思想是:证券在受到一定的信息冲击后,会产生后续的价格波动并有其相应的公允市价,就好比弹簧在一个力的作用下,能够围绕其均衡位置做有规律的运动,最终达到新的均衡。
4数据及实证检验
4.1数据描述
本文的数据以2015年6月13日证监会宣布清理配资作为股灾的起点,以8月14日证监会宣布股市企稳,国家停止托市作为股灾官方意义的结束。然后将2015年股市全年的数据用这一“历史”事件切开,分为股灾前(记为E1)和股灾后的数据(记为E2),最后用这两段数据研究股灾前后上证股指收益率的波动特征以及它们之间特征的变化。实证分析运用Eviews 6.0软件获得结果。
4.2实证分析
4.2.1统计描述
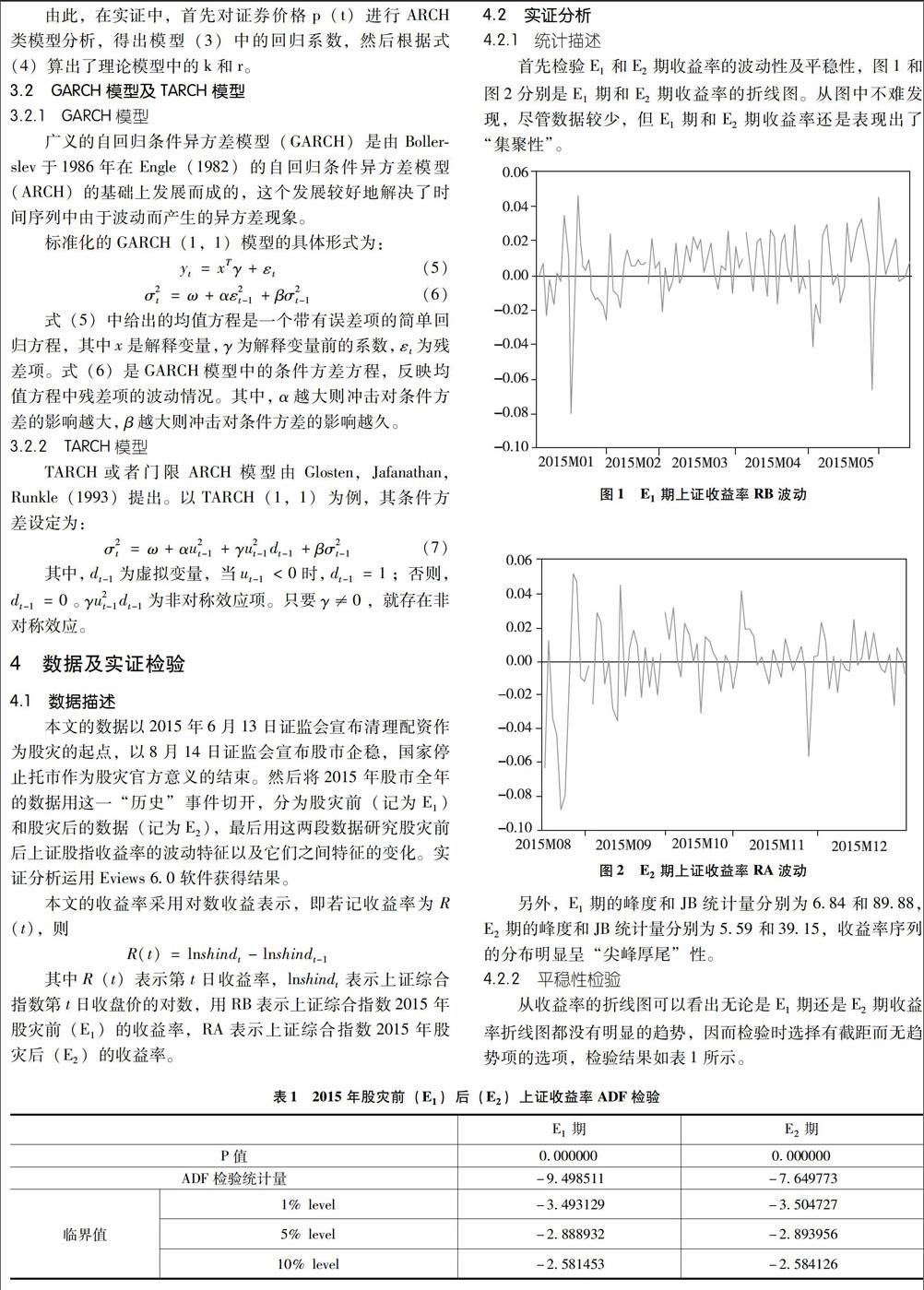
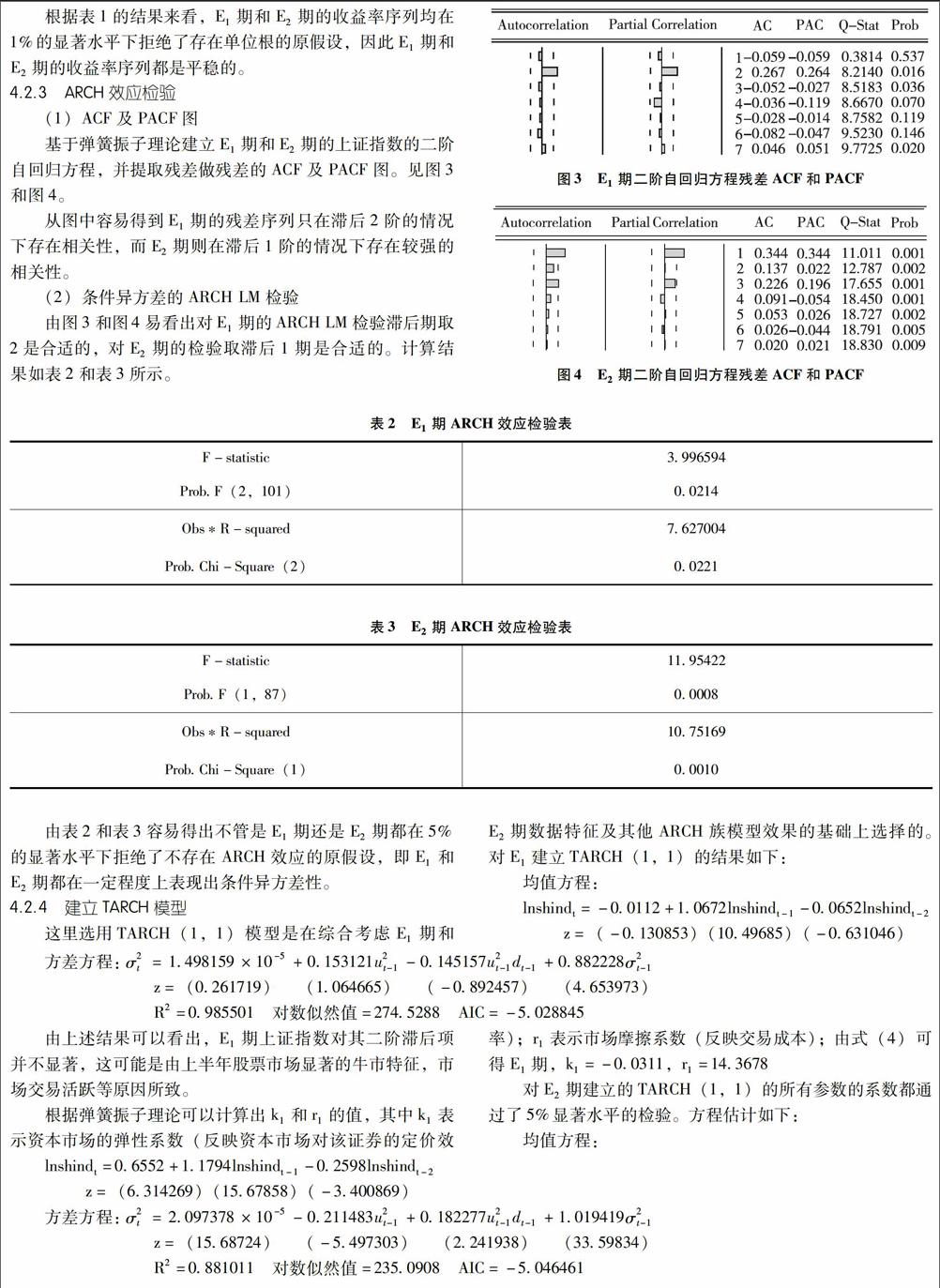
首先检验E1和E2期收益率的波动性及平稳性,图1和图2分别是E1期和E2期收益率的折线图。从图中不难发现,尽管数据较少,但E1期和E2期收益率还是表现出了“集聚性”。
另外,E1期的峰度和JB统计量分别为6.84和89.88,E2期的峰度和JB统计量分别为5.59和39.15,收益率序列的分布明显呈“尖峰厚尾”性。
4.2.2平稳性检验
从收益率的折线图可以看出无论是E1期还是E2期收益率折线图都没有明显的趋势,因而检验时选择有截距而无趋势项的选项,检验结果如表1所示。
根据表1的结果来看,E1期和E2期的收益率序列均在1%的显著水平下拒绝了存在单位根的原假设,因此E1期和E2期的收益率序列都是平稳的。
4.2.3ARCH效应检验
(1)ACF及PACF图
基于弹簧振子理论建立E1期和E2期的上证指数的二阶自回归方程,并提取残差做残差的ACF及PACF图。见图3和图4。
从图中容易得到E1期的残差序列只在滞后2阶的情况下存在相关性,而E2期则在滞后1阶的情况下存在较强的相关性。
(2)条件异方差的ARCH LM检验
由图3和图4易看出对E1期的ARCH LM检验滞后期取2是合适的,对E2期的检验取滞后1期是合适的。计算结果如表2和表3所示。
由表2和表3容易得出不管是E1期还是E2期都在5%的显著水平下拒绝了不存在ARCH效应的原假设,即E1和E2期都在一定程度上表现出条件异方差性。
4.2.4建立TARCH模型
这里选用TARCH(1,1)模型是在综合考虑E1期和E2期数据特征及其他ARCH族模型效果的基础上选择的。对E1建立TARCH(1,1)的结果如下:
由上述结果可以看出,E1期上证指数对其二阶滞后项并不显著,这可能是由上半年股票市场显著的牛市特征,市场交易活跃等原因所致。
根据弹簧振子理论可以计算出k1和r1的值,其中k1表示资本市场的弹性系数(反映资本市场对该证券的定价效率);r1表示市场摩擦系数(反映交易成本);由式(4)可得E1期,k1=-0.0311,r1=14.3678
对E2期建立的TARCH(1,1)的所有参数的系数都通过了5%显著水平的检验。方程估计如下:
5模型分析与结论
5.1TARCH模型分析
E1期即上半年的TARCH模型中,杠杆效应项的系数γ不显著地等于-0.145157,小于0,说明“好消息”能比“坏消息”产生更大的波动。当出现“好消息”时,该冲击会给lnshind带来一个0.153121倍的冲击,而出现“坏消息”时,仅会带来一个0.007964(0.153121-0.145157)倍的冲击。可以看出,尽管模型的参数并不显著但其经济意义并未违背上半年整体的一个牛市的特征。
E2期即下半年的TARCH模型中,杠杆效应项的系数γ=0.182277且显著,说明股票价格的波动具有明显“杠杆”效应:当出现“利好消息”时,会对股票价格指数带来一个-0.211483倍的冲击,而出现“利空消息”时,则会带来一个-0.029206(-0.211483+0.182277)倍的冲击。从两者的符号来看,很好地反映了下半年的恐慌心理,即无论利好还是利空市场都在下挫。但这里好像存在一个逻辑错误,即利空消息能比等量的利好消息产生更小的向下刺激动能。这可能和下半年投资者的“紧张兮兮”有关,因为“股灾”给投资者带来的伤害,导致投资者对任何一个“利好消息”都报以怀疑的态度,稍有不对就疯狂“逃命”,而“利空消息”的影响,从投资心理学及投资者结构角度考虑,可能的原因在于:投资者在亏损时,投资者会自然的存在行情逆转的幻想,尤其在亏损很大之后,由于害怕“踏空”(后悔厌恶),投资者会自然的进行心理暗示,导致对“利空消息”的“麻木”。而且,国内市场散户是市场的主导,这只会导致“麻木”的蔓延。
5.2弹簧振子模型分析
比较E1期和E2期的k值与r值,易发现反而是股灾后市场表现的更有效率及交易成本的降低,这和我们的预期可能并不一致。但细细思索又表现出一定的合理性,因为经过这一轮股灾之后,投资者“谨慎”地在市场中摸索,“小心翼翼”地“理性”地支配着其市场行为。对于任何的信息投资者都必然会思忖再三以期避免大的市场波动造成亏损,这有利于减少信息不对称所造成的市场摩擦及对市场的扭曲。
与之对应,上半年或许是国家牛市的盲目信赖,市场对各信息的反应往往缺乏理性,市场价格不能有效反映市场的真实状态,人们完全被情绪所掌控,造成上半年定价效率较低而且市场摩擦较大。下半年虽说市场处于一种极度的惶恐中,但投资者总算回归了一些理性——也许是过度理性,市场也逐渐回归于现有信息约束下的均衡,定价效率有所提高,摩擦有所减少。
参考文献:
[1]方璐.金融危机下上海股市非对称效应的实证分析[J].金融市场,2010(1).
[2]马鑫杰.基于信息不对称性反应的股票市场有效性实证研究[J].商业时代,2013(8).
[3]林德钦.创业板指数波动率预测效果比较研究——基于GARCH族模型[J].金融教学与研究,2014(1).
[4]万蔚,方孝感.我国沪、深股市的波动性研究——基于GARCH 族模型[J].价值工程,2007(10).
[5]何晓光,朱永军.中国 A股市场收益波动的非对称性研究[J].数理统计与管理,2007(1).
[6]张虎,鲁鸽.上证指数和香港恒生指数波动不对称性的实证比较[J].统计与决策,2013(23).
[7]赵贞玉,欧阳令南,祝波.弹簧振子理论及对上海股市的实证研究[J].管理科学学报,2007(6).
[8]高铁梅.计量经济分析方法与建模——EViews应用及实例(第二版)[M].北京:清华大学出版社,2009:193-218.

