基于BOPPPS模型下的高等数学微课教学设计
——以“一阶非齐次线性微分方程的解法”为例
储亚伟,叶薇薇,王海坤
(阜阳师范学院数学与统计学院,安徽 阜阳236037)
基于BOPPPS模型下的高等数学微课教学设计
——以“一阶非齐次线性微分方程的解法”为例
储亚伟,叶薇薇,王海坤
(阜阳师范学院数学与统计学院,安徽 阜阳236037)
BOPPPS模型是优秀的微课教学模型,是加拿大、台湾及国内高校教师技能培训中广泛采用的教学模式。同时,全国高校数学微课程教学设计竞赛的成功开展加快了传统课堂教学改革的步伐。为了有效地将数学微课程竞赛的先进理念及成果应用于课堂教学,不断深化教学改革、提高教学质量,文章以《高等数学》中“一阶非齐次线性微分方程的解法”为例,探讨基于BOPPPS模型的高等数学微课程教学设计的方法。设计理念是:将数学思想方法融入课堂教学;以学生为中心、以问题为导向的探究式教学;注重知识的认知过程,强调从已知到未知的自然过渡的互动式教学。
BOPPPS模型;高等数学;微课程;教学设计;特色
高等数学在高校课程中的重要性不言而喻,其教学效果的优劣将直接影响到高校的人才培养质量。随着“互联网+”及“慕课时代”的到来,高校传统课堂教学改革的力度也逐渐加大。在超星视频、爱课程、中国大学MOOC等不同形式在线课程平台推出的同时,由教育部高校大学数学课程教学指导委员会、全国高校教学研究中心、高校大学数学教学研究与发展中心共同主办的全国高校数学微课程教学设计竞赛的成功举办,为高校开展“微课程”教学搭建了学习与展示的平台,并将有力推动大学数学“微课程模式”的教学改革。为了将数学微课程竞赛的先进理念及优秀成果有效地应用到课堂教学,切实推动教育教学改革、提高教学质量,文章以《高等数学》[1]中“一阶非齐次线性微分方程的解法”的微课程设计(首届全国微课程教学设计大赛一等奖作品[2])为例,结合作者对BOPPPS教学工作的实践,探讨基于BOPPPS模式的高等数学微课程教学设计的方法。
一、BOPPPS模型概述
BOPPPS模型是加拿大教师技能培训中广泛采用的教学模式[3],是一个能够协助教师拆解并分析教学过程、发现教学盲点、提升教学成效的有效工具。根据学生专注力的持续时间(大约15分钟),该模型将教学内容拆分为独立的小单元 (不超过15分钟),每个教学小单元内都以达成教学目标为核心,构建了引言(Bridge-in)、教学目标(Objective/ Outcome)、前侧(Pre-assessment)、参与式互动教学(Participatory Learning)、后测 (Post-assessment)和总结 (Summary)等确保课堂成功的六大要素。按照BOPPPS模型的要求,一节45分钟的内容可以拆分为完整的三个单元,每个独立的单元从引言到总结一个完整的“起承转合”恰好构成一节微课。该模式为有效课堂教学提供了一个可操作的具体实践流程,使得课堂教学的安排更加条理化、合理化,也是进行微课程教学设计的有效工具[4]。
二、BOPPPS模型下高等数学微课设计理念——以“一阶非齐次线性微分方程的解法”为例
按照BOPPPS模型的要求,要进行高等数学课程的微课设计,需要先把该课程切割成独立的小单元。目前,高等数学课程已经形成了以知识点为单元的独立小单元模块[5-6],这为该课程的微课设计搭建了良好平台。为了实现有效教学,切实提高教学效果,我们的微课设计理念是:要在课堂教学中融入数学思想和方法的教学;强调以学生为中心、以问题为导向的探究式教学;注重知识的认知过程,强调从已知到未知的自然过渡和巧妙衔接的互动式教学。
以“一阶线性非齐次微分方程的解法”为例,在学习本小单元之前,学生已了解了一阶线性微分方程的概念,掌握了一阶线性齐次微分方程的解法。学完本节内容,不但完整地掌握了一阶线性微分方程的解法,也为下一节(Bernoulli方程)的学习奠定了基础。同时,一阶线性非齐次微分方程的解法与通解的结构可以推广至高阶的情形,因此这节课不但有承前启后的作用,也是学习Bernoulli方程及高阶线性方程的基础,是本章和本节的重点内容之一。然而,本节要介绍的“常数变易法”的引入太突兀,且没有介绍一阶线性微分方程通解的结构,既不利于学生对“常数变易法”的理解与接受,也不利于高阶线性微分方程的学习。
另一方面,在教学中突出数学思想、问题式学习、探究式学习等是教学改革中着力倡导的新型学习方式。结合大纲的要求,在设计本课时,希望通过问题激发学习兴趣,透过探究对比自然引出重要方法——常数变易法,通过细心观察总结一般规律——非齐次线性微分方程通解的结构,在问题解决及实例中多次强调转化、化归的数学思想,同时利用多媒体辅助教学,破重点、化难点。
三、基于BOPPPS模型下“一阶非齐次线性微分方程的解法”的教学设计:
(一)(Bridge-in)——问题导入
以学生已掌握的两个知识点为抓手,先从第一个知识点引出问题:一阶非齐次线性微分方程的一般形式

若Q(x)≡0,称(1)为齐次的;若Q(x)≠0,称(1)为非齐次的。由已知齐次方程的解法引出核心问题:非齐次方程(1)的解法。
(二)教学目标(Objective/Outcome)——PPT展示
1.知识能力目标
理解“常数变易法”的由来,掌握解非齐次方程(1)的常数变易法的步骤;理解方程(1)通解的结构;较为熟练地运用常数变易法及通解公式求解非齐次线性微分方程。
2.思想方法目标
通过分类求解一阶线性微分方程,培养学生的分类讨论与化归与转化思想;通过探究非齐次方程通解可能具有的形式,引导学生进行探究性学习。
(三)前侧(Pre-assessment)——提问并板书
提问:方程(1)对应齐次微分方程的通解?
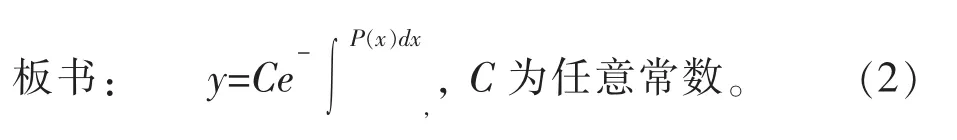
通过类比,引出本节课内容。
(四)参与式互动教学(Participatory Learning)——特色设计
1.常数变易法
为重现知识的认知过程,做好从已知到未知的自然过渡和有效衔接,本段从学生熟知的分离变量法及方程(1)对应齐次方程的通解入手,采取问题导向的互动式、参与式的探究教学模式。

这样,我们便共同探索出方程(1)通解的形式,这是讲解常数变易法的关键[7-8]。类比对应齐次微分方程的通解形式(2),自然地得到常数变易法,其本质是未知函数的变量代换。
2.通解公式
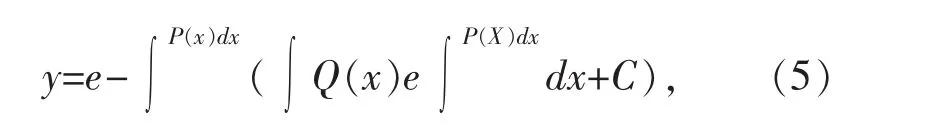
其中,C为任意常数。
3.通解结构
通过发问,请同学根据通解公式(5)总结出方程(1)的通解结构:
非齐次线性微分方程的通解等于对应齐次方程的通解加上非齐次方程的一个特解。
(五)后测(Post-assessment)——课堂练习
例1 使用常数变易法求方程

例2 使用通解公式求方程(y2-4x)dy=2ydx的通解。
(六)总结(Summary)——强调思想、拓展方法
利用ppt动态展示,并强调化归思想,拓展方程(1)的解法:
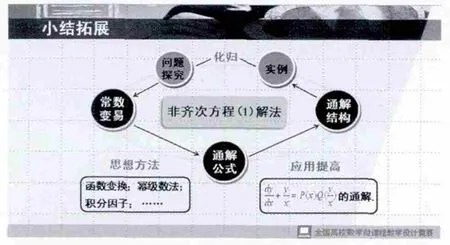
四、应用反思
上例从问题的引入、方程通解形式探究,到通解结构的总结与解法拓展,结合了问题式、探究式的学习方法进行讲授,使得常数变易法得以自然引出,顺利地克服了难点。拓展部分结合论文的成果,补充了两种解法,利于开拓学生的视野。
在高等数学的教学过程中,教师完全可以以知识点为独立模块,按照BOPPPS教学模型精心设计每一个知识点的单元微课,再把各知识点连接起来,真正做到以学生为中心、以问题为导向、以有效实现教学目标为核心,在课堂教学中融入数学思想方法、在新知讲授前搭建过渡桥梁,有效克服难点、突出重点,充分利用微课程资源(PPT、微视频等),实现有效课堂教学。
[1]同济大学数学系.高等数学(上册)[M]7版.北京:高等教育出版社,2014:314-315.
[2]首届(2015)全国高校数学微课程教学设计竞赛[EB/ OL].[2015-10-30].http://www.icourses.cn/zlgc/wkc/weike. html.
[3]曹丹平,印兴耀.加拿大BOPPPS教学模式及其对高等教育改革的启示[J].实验室研究与探索,2016,35(2):196-201.
[4]丁轩,徐莉.基于BOPPPS教学模型的肿瘤科临床带教微课程体系建设及应用[J].中国护理管理,2016(5):659-662.
[5]高等数学 (上)知识点细分目录 [EB/OL].[2015-12-30].http:// wenku.baidu.com/link url=BOFcJt9rLu_M8GiQFy7VQPsx1Y8UQQ-fUDy33lYN1gSezuXapxmYAaw4swgyGggsyTaj81XfCTf5OVy9 -AE5h6jqfZEhJAIsDvjwkoqb2HfG.
[6]高等数学(下)知识点细分目录[EB/OL].[2015-07-24].http://wenku.baidu. com/linkurl=Jf2Er7rMnbl3uMpCZu7cYnI8S2L2Ip8GMzSVGXNHgPRtq _JDP-cYw1ONpuAFU4Mup9dx9Oi5DDBZFVmghSsHFsDXbjmSjvWdF6Uu_v_clBQa.
[7]杨芳.关于常数变易法的教学探讨[J].高师理科学刊, 2010,30(2):92-95.
[8]鲜大权.一阶线性常微分方程解法及教学[J].高等数学研究,2007,10(3):12-14.
编辑:崔月华
Microlecture teaching design of higher mathematics based on the BOPPPS teaching model——with the example of“the first order non-homogeneous linear differential equation”
CHU Yawei,YE Weiwei,WANG Haikun
(School of Mathematics and Statistics,Fuyang Normal University,Fuyang Anhui 236037)
The teaching model of BOPPPS,which is widely used for improving the teaching abilities in Canadian,Taiwanese and domestic universities is excellent.Meanwhile,the success of the first microlecture teaching design competition for university mathematics in universities and colleges in China is quickening the steps on traditional classroom teaching models.In order to apply the advanced ideas and excellent achievements of this competition to classroom,to constantly deepen reformation of teaching and improve teaching quality,in this paper we explore a method for microlecture teaching design of higher mathematics based on the BOPPPS teaching model,with the example of “the first order non-homogeneous linear differential equation”.Our design idea includes merging mathematics thought and method into class teaching,the teaching method of inquiry of student-centered and problem-oriented,employing the interactive teaching methods,which focuses on the cognitive process of knowledge and the natural transitionfrom known to unknown.
BOPPPS teaching model;higher mathematics;microlecture;teaching design;feature
G623
:A
:2095-7327(2016)-09-0153-04
储亚伟(1977-),男,安徽阜阳人,阜阳师范学院副教授,博士,研究方向:几何分析。
安徽省教学团队项目“大学数学课程教学团队”(编号:2015jxtd121);安徽省专业综合改革试点项目“数学与应用数学”(师范类)(编号:2014zy138);安徽省重点教研项目 “创新人才培养模式下微分几何学的教改与实践”(编号:2013jyxm553)。

