Development of a bifurcation analysis approach based on gPROMS platform☆

Xueqing Kang,Hongye Cheng,Liwei Tong,Lifang Chen,Zhiwen Qi*

Max Planck Partner Group at the State Key Laboratory of Chemical Engineering,School of Chemical Engineering,East China University of Science and Technology,Shanghai 200237,China

1.Introduction

Design and control of chemical processing systems that achieve optimized performance such as profit and safety calls for the development of advanced methods and tools for identifying the fundamental features of the processes,especially the bifurcation behaviors[1–3].The characteristics of chemical processes are usually modeled by mathematic equations which are commonly nonlinear regardless of whether they are algebraic,transcendental and/or differential.Very often,nonlinear algebraic and transcendental equations may have multiple steady state(MSS)solutions.The three types of MSS defined by Gani and Jørgensen[4]could result in several problems in practice.For example,for control of process operation,MSS usually results in the phenomenon of hysteresis,in which the important performance of the process,e.g.product purity and selectivity,will jump to another branch when the operation parameter passes through a turning point.And it is even not able to return back to the initial branch by reversing the operation parameter.Such a complicated procedure could bring on the delay of operation or trigger wrong control action that may generate catastrophic results in chemical engineering systems.Even if it does not occur,the existence of MSS could cause the erratic behavior in systems by transition between two different steady state branches,as reported by Kovach and Seider[5].In addition to MSS,Hopf bifurcation points are usually found and considered in chemical processes[6,7].Thus,it is essential to discover the possibility of multiplicity of the process and figure out all multiple solutions within the user-defined domain of operating variables.

The most commonly applied process simulators like ASPEN PLUS,HYSYS,PRO/II,and CHEMCAD have the common advantages of fruitful property databases,thermodynamic and process unit models,and advanced numerical solvers,etc.However,they have no bifurcation algorithms for tracing all steady-state solution branches,getting all solutions and performing a stability analysis(by evaluating the eigenvalues of the Jacobian matrix).In some cases,multiple solutions might be found by performing a sensitivity analysis on one or more parameters,or varying the initial guess of the unknowns.When a process indeed has MSS behavior,these methods are very trivial and might fail to converge during the simulation of processes since the Jacobian matrix becomes singular at bifurcation points.Moreover,acquisition of only one solution could result in misleading conclusions and decisions because of the elimination of certain eligible,and possibly,more feasible design alternatives.In order to compensate for the above drawbacks,a lot of works are reported to develop procedures for the construction of the bifurcation diagrams.Leiet al.[8,9]found two steady states for the alkylation of benzene with propylene by suspension catalytic distillation and also analyzed MSS for other special distillation processes[10,11].Nevertheless,the main contributions of Leiet al.[8–11]are limited in the research of distillation.Yang et al.[12]and Li et al.[13]used the method of sensitivity analysis tool built in ASPEN PLUS to discover the input and output multiplicity in reactive distillation.Nevertheless,it still required appropriate initial guess to reach the specified branch.Vadapalli and Seader[14]implemented the arc-length continuation algorithm as a FORTRAN subroutine in ASPEN PLUS for computing bifurcations diagrams.However,it is impossible to detect the exact bifurcation points and verify whether the steady state is stable or unstable since it is based on Jacobian matrix-free algorithm.Restrepoet al.[15]developed a bifurcation framework which used Visual Basic to create a COM server and thus link MATLAB and Aspen Dynamics(AD)/Aspen Custom Modeler(ACM).The bifurcation algorithm was coded in MATLAB and the chemical process models were implemented in AD/ACM,which could perform quick bifurcation analysis.In addition,mathematics simulators(e.g.,AUTO,CONT,HOMPACK,PITCON and MATLAB)that include continuation algorithms are feasible approaches for finding all the solutions[14].However,these tools were developed specially for investigating mathematic problems,which requires expenditure of much effort on writing and debugging codes such as thermodynamic and process models into the software when dealing with chemical engineering problems.Therefore,it is crucial for developing an approach that could contain and take the advantages of both process and mathematics simulators.

The advanced process simulator gPROMS is a promising candidate to achieve the goal.As a chemical process simulator,gPROMS has a model library of standard operation units and is very easy to build new models coded in a symbolic form for s specific chemical problems which were fully demonstrated in our previous work[16,17].Especially,the mathematical information of models such as Jacobian matrix is accessible to user by Foreign Process Interface(FPI)[18],which makes it possible to implement various algorithms to perform bifurcations analysis.Meanwhile,the stability of solutions could be verified by analyzing the eigenvalues of the Jacobian matrix.Therefore,in this work,an approach of bifurcation analysis is constructed based on gPROMS platform.The arc-length continuation algorithm incorporated as a process entity in gPROMS is used to get all of the steady state solutions of processes while the corresponding Jacobian matrix is evaluated by a bifurcation test function τ to detect if it is a bifurcation point.The feasibility and capacity of the proposed methods is proved by two chemical engineering processes from literature,i.e.,a classic adiabatic CSTR and a homogenous azeotropic distillation.

2.Methods

2.1.Design of algorithms in gPROMS platform

The commonly used method to achieve all possible solutions of the nonlinear equations in engineering is continuation algorithms combined with the bifurcation theory[19].However,in commercial process simulators,such algorithms are not provided,and users have to develop user-defined algorithms such as arc-length continuation method to achieve it.For designing a reliable algorithm,it is inevitable to acquire and evaluate the mathematic information of equations(i.e.,Jacobian matrix).gPROMS provides users with access to mathematic information of models by FPI which gives a general mechanism for the exchange of information between gPROMS and external software.The FPI contains a set of elementary communication tasks and a communication protocol between gPROMS and the external software.The linearization task[18]gives a means of using non-linear models that are coded in gPROMS and are of arbitrary complexity for control-system design using linear analysis techniques coded.In the models of gPROMS,it comprises mixed sets of non-linear differential and algebraic equations that can be written in the form of Eq.(1)

where X(t)and Y(t)are the sets of differential and algebraic variables,respectively;˙X（t）are the derivatives of X(t)with respect to timet;U is the set of input variables that are given functions to time.By linearizing the above equations,a linear model of the form is as Eq.(2)and(3):

where the values of A,B,C and D can be directly exported through FPI.Thus,the Jacobian matrix of systems can be acquired by users,which gives a chance of developing continuation algorithms based on gPROMS platform.

As in Fig.1(left),gPROMS connects model equations and algorithms through running process entity.Meanwhile,it provides capabilities and open interfaces for compiling user-defined algorithms which are written by procedural language,such as FORTRAN,C and C++,and wrapped in the form of dynamic link library(.dll).However,such a method is very complicated and time consuming because the procedural language is not friendly to users.Thus,the concept of establishing algorithms based on gPROMS platform is proposed,as shown in Fig.1(right).The algorithms are directly written in the schedule section of process entity of gPROMS by various tasks,e.g.,linearization,reassign,and replace.During the calculation,the function information such as values of variables could be invoked by commands in schedule section.Nevertheless,as the Jacobian matrix could not be directly called by the process entity,a foreign object is introduced as a transfer station to save the Jacobian matrix and convey it to algorithms in the process entity.

2.2.Development of continuation method for bifurcation analysis in gPROMS

As described above,it is feasible to develop algorithms in gPROMS.Here,an arc-length continuation method is established while calculating bifurcation points which are checked by values of a bifurcation test function τ.The overall calculation procedure is illustrated in Fig.2,which is divided into five steps.

(1)Define the state variables X and intermediate(help)variablesH(X)in the model equations.Only the state variables X are set as iteration variables in the foreign object algorithm.Meanwhile,the bifurcation parameter λ and its user-defined domain[λ0,λend]are specified.

(2)Trace a branch from one set of steady state solutions calculated by the built-in solvers in gPROMS.The corresponding Jacobian matrix is exported into a foreign object algorithm compiled by C++where a bifurcation test function τ(X,λ)is evaluated to judge whether the bifurcation parameter λ reaches bifurcation point λ0.

(3)Several bifurcation test functions(see Section 2.4)are successively evaluated to define the type of bifurcation points.If there doesn't exist any bifurcation point,continue calculating the next step at λi+1by increasing a small step Δλ with gPROMS built-in solvers until λ is beyond the user-defined domain[λ0,λend].In the case that a turning point is detected,it will switch to the arc-length continuation method to overcome the failure of convergence caused by turning points.

(4)Check if the turning point λ0is passed after each converged point in arc-length continuation.Theoretically,the whole calculation procedure could be achieved by arc-length continuation alone.However,the built-in algorithms in gPROMS are more efficient.Thus,the speed and efficiency of calculation can be significantly enhanced by coupling them.Once the bifurcation parameter λipasses the turning point and switches to another branch,the latest solution(Xi,λi)will be considered as the initial values and the described procedure in step 2 will be repeated.

(5)For each converged point,the stability analysis is achieved by the evaluation of eigenvalue in Eq.(4)

where e is the unit matrix,μ is the eigenvalue,and w the corresponding eigenvector(the detail in calculation is described in Section 2.4).

Fig.1.Design of algorithms based on gPROMS platform.

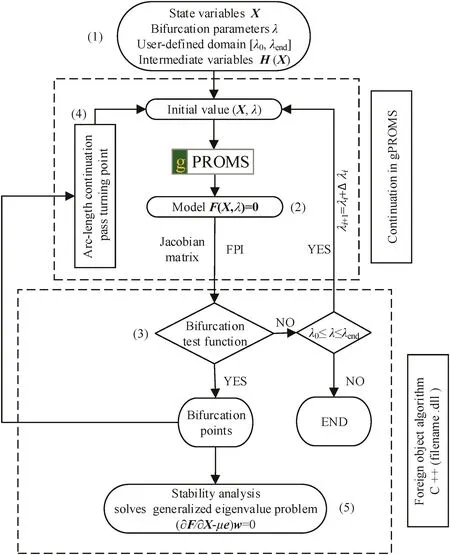
Fig.2.The overall calculation procedure of continuation method for bifurcation analysis.

2.3.Implementation of arc-length continuation in gPROMS

When it is desired to perform continuation of a problem at parameter values in the region of a stability limit(i.e.,near a turning point),difficulties arise as the Jacobian matrix approaches singularity.The arc-length continuation algorithm developed by Keller[20]could alleviate the singularity by augmenting the system with an alternate arc length parametersand an arc length equation n,in which the augmented system

where J=∂F/∂X are computed during each iteration step.The typically sparse nature of J is exploited by performing one resolve per iteration which refers to previous literature[21,22]:

where a and b are temporary vectors.The new updates are then found by:

In order to implement this scheme into gPROMS,it is necessary to access the derivative information,i.e.,J is the Jacobian matrix of the model functions with respect to state variables X.In gPROMS,both of them can be acquired by the linearized task(i.e.,Eq.(2)where U is defined as parameter λ).Thus,the values of A(or C)in Eq.(2)(or Eq.(3))are equal to J,respectively.As described in Fig.1,a foreign object is used to convey Jacobian matrix to the arc-length continuation procedure coded in the process of entity where a Newton–Raphson method is used as corrector.If a solution cannot be found for the current parameter value,the step size is reduced by half until an expected very small value(i.e.,close to zero)of τ is reached.

2.4.Calculation of bifurcation points and stability analysis

Normally,there are two methods for calculating bifurcation points,i.e.,direct and indirect methods,where the latter is applied in this work.A bifurcation test function τ(X,λ)is evaluated during the branch tracing and a bifurcation point is usually located by zero of τ.That is,a bifurcation test function satisfies the property τ(X0,λ0)=0 and is continuous in a sufficiently large interval that includes λ0.The test function τ has several different forms where some cases are very clear but others are defined in an artificial way[23].A clear choice of τ is related to the eigenvalues αk+iβkof the Jacobian matrix where akand βkare the real and imaginary parts of the eigenvalues,respectively.τ1is defined as the maximum value ofak,as shown in Eq.(12).

This approach has the advantage of being physically meaningful because τ1＜0 guarantees local stability.It is able to locate the turning point since the branches change stability at every turning point.Meanwhile,it also indicates Hopf bifurcation point because bifurcations to periodic solutions are related to conjugate complex eigenvalues passing the imaginary axis.Another bifurcation test function is especially designed for turning points which are commonly observed in the chemical engineering process.It is defined by Seydel[24]that is summarized as the following equations:

where the vector h satisfies Alkh=elin which eldenotes the l th unitvector in ℝn.Alkis the Jacobian A with thelth row replaced by ek.As reported by Seydel[24],in practice,the choice of the indexeslandkis not problematic.The choice is even arbitrary in many cases.

All bifurcation test function and eigenvalues are implemented in a foreign object algorithm where the package LAPACK[25]is applied to calculate Jacobian matrix at each steady state.

2.5.Advantages of the proposed approach

Compared with the bifurcation analysis approaches in mathematic tools and developed in process simulators,the proposed methods in this work have several advantages.

(1)The methods make complete use of gPROMS program(i.e.,process unit models,thermodynamic equations and numerical solvers),thus saving the work of supplying additional codes.

(2)The algorithm is implemented in a continuous manner,moving from one solution branch to another automatically.The existence of a new branch could be confirmed by checking the value of test function τ.If the approach retraces an old solution branch,the user can adjust the parameters in the algorithm to restart calculations for the new branch.

(3)The stability of the solutions could be acquired by analysis of the Jacobian matrix of the system that is accessible to user in gPROMS.

(4)The methods can detect the exact locations of bifurcation points.When test function τ is close to zero,small step size is used until the value of τ reaches zero.

3.Application Examples

Two examples are used to test the feasibility of method developed above.In example 1,a classic adiabatic CSTR is investigated where the CSTR model is directly invoked by the model library in gPROMS.In example 2,a homogenous azeotropic distillation for mixture of methanol,toluene and methyl butyrate is analyzed,which is also studied theoretically and experimentally by Leeet al.[26]and Thomaset al.[27],respectively.

3.1.Adiabatic continuous stirred-tank reactor

One of the simplest chemical processes that occurs multiplicity is the unit operation of CSTR.gPROMS model library has a standard CSTR model which can be used directly for this example.

A liquid phase hydrolysis of propylene glycol in an adiabatic CSTR as described by Vadapalli and Seader[14]is employed as a case study.The reaction is

Propylene oxide （ A）+water（ B）→propylene glycol（ C）

where the reaction rate is second order with respect to propylene oxide.

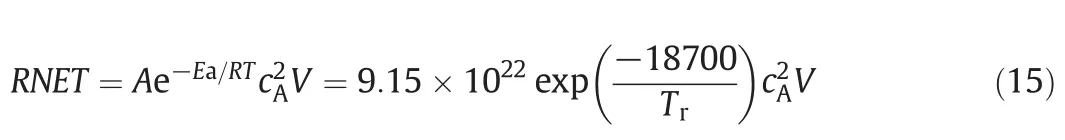
where cAis molar concentration in the unit of kmol·m-3;V is the reactor volume in the unit of m3.

The reactor configuration and feed specification for simulation are summarized in Table 1,the volumetric flow rate of water is selected as the bifurcation parameter λ.Since methanol does not participate in the reaction,its mass balance is neglected in the model equation.Thus,four nonlinear equations(3 mass balances and 1 energy balance)will be solved in whichcA,cB,cCandTr(4 variables)are used as state variables X.The branch tracing for bifurcation analysis is started from λ =5.4 m3·h-1with initial values ofcA=0.081 kmol·m-3,cB=34.76 kmol·m-3,cC=2.26 kmol·m-3andTr=350 K.

Table 1Simulation configuration of the adiabatic CSTR problem

The computed bifurcation diagrams of the reactor temperature and the exit concentration for propylene glycol and propylene oxide against the bifurcation parameter(namely,volumetric flow rate of feed water)are showed in Fig.3.As seen in Fig.3B,the reactor temperature falls rapidly from 348.40 to 323.43 K as flow rate of water increases along branch I from the starting point of 5.4 m3·h-1until the first turning point is encountered at 7.74 m3·h-1.After the first turning point,branch II is traced and the temperature continues to fall,as the flow rate decreases,until reaching the second turning point 5.92 m3·h-1.Thereafter,branch III is calculated and the temperature drops slowly(303.25 to 298.48 K)while the flow rate begins to increase.Fig.3A is similar to 3B since the production of propylene glycol depends on the rate of the reaction which is dominated by the temperature of the reactor.In contrast,Fig.3C is opposite to Fig.3B as a result of the restriction of mass balance and reaction equations.

The corresponding bifurcation test function τ2for(l,k=4)detecting turning points is illustrated in Fig.3D.As seen,the test function is able to efficiently locate the turning points as it gradually approaches to zero when the branch is about to reach the turning points.

The stability analysis of the three branches is shown in Fig.4 where the corresponding four eigenvalues of the Jacobian matrix are plotted against the flow rate of water.The eigenvalues are all real in which eigenvalues 2 and 3 are equal and plotted in Fig.4B.In Fig.4A and B,eigenvalues 1,2 and 3 are always negative for the three branches.Fig.4C indicates that eigenvalues 4 are all negative at branches I and III except for branch II.Therefore,steady state solutions of branch I and III are stable while they are unstable for branch II,which is consistent with the results of Vadapalli and Seader[14].However,the two turning points are slightly different from literature,i.e.,6.04 and 7.79 m3·h-1by AUTO,and 5.71 and 7.84 m3·h-1by ASPEN PLUS.This may be attributed to the reduced form of energy balance equation in AUTO and the difference of property database between ASPEN PLUS and gPROMS.Consequently,the approach based on gPROMS in this work integrates the advantages of both built-in process simulators and imported mathematic subroutine solvers that can efficiently achieve exact bifurcation analysis.

3.2.Homogenous azeotropic distillation

Fig.3.Bifurcation diagram of different variables against the volumetric flow rate of water.(A)Exit concentration of propylene glycol;(B)exit concentration of propylene oxide;(C)temperature;(D)bifurcation test function τ2;stable steady state(straight line);unstable steady state(dashed line).

Fig.4.Eigenvalues against volumetric flow rate of water.(A)Eigenvalue 1;(B)Eigenvalue 2,3;(C)Eigenvalue 4;stable steady state(solid line);unstable steady state(dashed line).

Distillation is one of the most important separation processes in chemical industries.Compared to CSTR,models for distillation orspecial distillation(e.g.azeotropic,extractive and reactive distillation)are much more complicated with a large amount of variables.For the ternary mixture of methanol,methyl butyrate and toluene,multiple steady states are observed experimentally[27]and limit cycles are predicted by an open-loop homogeneous azeotropic distillation model[26].Here,this azeotropic distillation process is studied to check the feasibility of the proposed approach.

An azeotropic distillation model is adapted with the same CMO(constant molar over flow)assumptions and configurations as reported by Leeet al.[26].The vapor phase is assumed to be ideal,and liquid activity coefficients are predicted by the Wilson model.The physical property methods and parameters are taken from gPROMS database.As the CMO model neglects energy balances,the state variables X in this model arexi,j(mass fraction of componentiat trayjin liquid phase;i=1,2…NC-1 with NC the total number of the components;j=1,2…NG with 1 the condenser and NG the reboiler)andTj(temperature at trayj).The column configuration and feed specification for simulation are shown in Fig.5.The distillation flow rate(D)is selected as the bifurcation parameter λ which is started from λ =86 kmol·h-1to 100 kmol·h-1for bifurcation analysis.

The computed bifurcation diagrams of the temperature in column bottom and the mole fraction of toluene in distillate and bottom against the bifurcation parameter λ(namely,the distillate flow rate)are given in Fig.6.Two turning points are detected at 87.55 and 99.00 kmol·h-1,respectively.As illustrated in Fig.6B,along with branch I,the bottom temperature rises slowly from 336 K to 340 K as the flow rate increases to 97 kmol·h-1.Then,the temperature rises steeply from 340 K to 380 K until the first turning point is reached at 99.0 kmol·h-1.Beyond that point,branch II is calculated and the temperature continues to rise,as the distillate flow rate decreases,until reaching the second turning point 87.55 kmol·h-1.Beyond the second turning point,the distillate flow rate begins to increase again while the temperature almost keeps constant at 383.8 K.Fig.6C and B show the similar tendency because the toluene as heaviest component dominates the temperature in the bottom.Fig.6A is opposite to Fig.6C due to the restriction of mass balance.The MSS bifurcation behaviors are very close to the theoretical analysis[26]and experimental study[27].

Fig.5.Simulation configuration of the azeotropic distillation column.

Fig.6.Bifurcation diagram of different variables against the distillate flow rate.(A)Liquid mole fraction of toluene in the distillate;(B)liquid mole fraction of toluene in the bottom;(C)bottom temperature;(D)bifurcation test function τ1;stable steady state(straight line);unstable steady state(dashed line);Hopf bifurcation points(■).

Moreover,the Hopf bifurcation is also discovered.As seen in Fig.6D,the bifurcation test function τ1at branch III indicates that the maximum of all real parts of eigenvalues of the Jacobian matrix is over zero at the range from 89.67 and 97.82 kmol·h-1.This means that the solution loses its stability at the above range.However,the points of 89.67 and 97.82 kmol·h-1are not turning points as no other branch is found after passing them.Further analysis finds that there exists a pair of conjugate complex eigenvalues passing the imaginary axis at the two points.Thus,two Hopf bifurcation points are located at 89.67 and 97.82 kmol·h-1.

To illustrate the phenomenon of the Hopf bifurcation,a dynamic simulation is executed atλ =97 kmol·h-1.Fig.7 reveals the responses of temperature and liquid mole fractions on tray 12 at unstable steady state of branch III where a perturbation of re flux flow rate(10 kmol·h-1)is introduced.As a result,the periodic oscillation,at interval of37 h,occurs and the compositions and temperature vary significantly,e.g.,the mole fraction of methanol from 0.0050 to 0.9957.The periodicity with a double peak of the methyl butyrate fraction is also illuminated in literature[26].

The detailed discussion of the bifurcation analysis is illustrated in Fig.8 where the average temperature of all the trays,the reboiler,and the condenser is selected as the horizontal axis variable.The bifurcation parameter distillate flow rate is divided into four regions(R)according to their different steady state and dynamic behaviors.The vertical distance between the dots represents the amplitude of the limit cycles at the certain bifurcation parameter in the region(R III).The coalescence of limit cycles with branch II essentially causes the limit cycles to disappear,and similar phenomenon is illustrated in the distillation process for the ternary mixture of acetone-benzene-heptane[28].The detailed descriptions are as follows:

R I(one steady state):λ＜A(87.55)orλ＞F(99.00).In this region,

only a single stable steady state exists on branch I and III,respectively.Neither MSS nor oscillation caused by variation of bifurcation parameter or perturbation occurs in this region.R II(three steady states,no Hopf bifurcation):A(87.55)＜λ＜B(89.67)andE(97.82)＜λ＜F(99.00).Three steady states exist but no periodic oscillations occur on branch III.The steady states on branch I and III are stable while they are unstable on branch II.R III(three steady states,limit cycle):B(89.67)＜λ＜C(92.02)andD(96.91)＜λ＜E(97.82).The steady states at the branch I are stable while they are unstable at other branches.Oscillations occur at branch III which are surrounded by stable limit cycle.The amplitude of limit cycles around the branch III grows until the limit cycles touch the branch II and disappear.R IV(three steady states,homoclinic bifurcation):C(92.02)＜λ＜D(96.91).This region is bounded by two homoclinic bifurcation points where the limit cycles disappear.This results in one stable and two unstable steady states,of which the former is the only attractor.

Fig.7.Responses of temperature and liquid mole fractions on tray 12 at unstable steady state of branch III where a perturbation of re flux flow rate is introduced(D=97).

Fig.8.Bifurcation diagram of the average temperature against the distillate flow rate.

To demonstrate the homoclinic bifurcation occurring in R IV,the responses of the average temperature at branch III with different values ofDis illustrated.As seen in Fig.9A,with increasingD,the average temperature keeps stable in R II,generates oscillation in R III and falls to branch I in R IV as the amplitude of oscillation is beyond the branch II.Similar situation happens with decrease ofD,as shown in Fig.9B.

Two case studies are executed successfully on PC(operating system of Windows 7,IntelE7500 CPU).The CPU time is 16.37 s and 36.24 s,respectively.The predicted results of both MSS and limit cycle are the same as literature[14,26],which suggests that the developed bifurcation algorithm based on gPROMS platform is feasible and reliable.Moreover,the discovered homoclinic bifurcation in case 2 by accurate bifurcation analysis indicates that the proposed method is powerful.

4.Conclusions

Fig.9.Responses of the average temperature to consecutive changes of D at branch III.(A)Increase D;(B)Decrease D.

A method for bifurcation analysis based on gPROMS platform has been proposed.The method consists of an arc-length continuation algorithm coded in the process entity of gPROMs and several bifurcation test functions are wrapped in the foreign object.All the multiple steady state solutions can be calculated by coupling the arc-length continuation and built-in solvers in gPROMS while the corresponding bifurcation points are located by the bifurcation test function.The stability of solutions can be determined by the analysis of Jacobian matrix which is directly exported by FPI.Two examples are successfully tested where the bifurcation points such as turning points and Hopf bifurcation points are determined by the method.The results are in good agreement with literature and even more complicated bifurcation behavior can be discovered.Therefore,the developed method of continuation algorithms for tracking multiple solutions and bifurcation analysis in gPROMS is feasible and efficient for general chemical processes.

[1]B.P.Patil,E.Maia,L.A.Ricardez-Sandoval,Integration of scheduling,design,and control of multiproduct chemical processes under uncertainty,AIChE J.61(2015)2456–2470.

[2]Nan Zhang,Tong Qiu,Bingzhen Chen,Bifurcation control and eigenstructure assignment in continuous solution polymerization of vinyl acetate,Chin.J.Chem.Eng.23(2015)1523–1529.

[3]H.Z.Wang,Z.H.Yuan,B.Z.Chen,X.R.He,J.S.Zhao,T.Qiu,Analysis of the stability and controllability of chemical processes,Comput.Chem.Eng.35(2011)1101–1109.

[4]R.Gani,J.B.Jørgensen,Multiplicity in numerical solution of non-linear models:Separation processes,Comput.Chem.Eng.18(1994)S55–S61.

[5]J.W.Kovach,W.D.Seider,Heterogeneous azeotropic:Experimental and simulation results,AIChE J.33(1987)1300–1314.

[6]H.Z.Wang,N.Zhang,T.Qiu,J.S.Zhao,X.R.He,B.Z.Chen,Analysis of Hopf points for aZymomonas mobiliscontinuous fermentation process producing ethanol,Ind.Eng.Chem.Res.52(2012)1645–1655.

[7]H.Z.Wang,N.Zhang,T.Qiu,J.S.Zhao,X.R.He,B.Z.Chen,A process design framework for considering the stability of steady state operating points and Hopf singularity points in chemical processes,Chem.Eng.Sci.99(2013)252–264.

[8]Z.G.Lei,B.H.Chen,Z.W.Ding,Special Distillation Processes,Elsevier,Amsterdam,2005.

[9]Z.G.Lei,J.F.Yang,J.J.Gao,B.H.Chen,C.Y.Li,Gas–liquid and gas–liquid–solid reactors for the alkylation of benzene with propylene,Chem.Eng.Sci.62(2007)7320–7326.

[10]Z.G.Lei,C.N.Dai,J.Q.Zhu,B.H.Chen,Extractive distillation with ionic liquids:a review,AIChE J.60(2014)3312–3329.

[11]Z.G.Lei,C.Y.Li,B.H.Chen,Extractive distillation:A review,Sep.Purif.Rev.32(2003)121–213.

[12]B.Yang,J.Wu,G.Zhao,H.Wang,S.Lu,Multiplicity analysis in reactive distillation column using ASPEN PLUS,Chin.J.Chem.Eng.14(2006)301–308.

[13]S.Li,D.Huang,Simulation and analysis on multiple steady states of an industrial acetic acid dehydration system,Chin.J.Chem.Eng.19(2011)983–989.

[14]A.Vadapalli,J.D.Seader,A generalized framework for computing bifurcation diagrams using process simulation programs,Comput.Chem.Eng.25(2001)445–464.

[15]J.B.Restrepo,G.Olivar,C.A.Cardona,Bifurcation analysis of dynamic process models using aspen dynamics and aspen custom modeler,Comput.Chem.Eng.62(2014)10–20.

[16]L.W.Tong,W.G.Wu,Y.M.Ye,G.Wozny,Z.W.Qi,Simulation study on a reactive distillation process of methyl acetate hydrolysis intensified by reaction of methanol dehydration,Chem.Eng.Process.67(2012)111–119.

[17]L.W.Tong,L.F.Chen,Y.M.Ye,Z.W.Qi,Analysis of intensification mechanism of auxiliary reaction on reactive distillation:methyl acetate hydrolysis process as example,Chem.Eng.Sci.106(2014)190–197.

[18]gPROMS Foreign Objects and Foreign Processes 3.5.0,Process Systems Enterprise Ltd.,London,U.K.,2011 23–32.

[19]R.Seydel,V.Hlavacek,Review article number 24:role of continuation in engineering analysis,Chem.Eng.Sci.42(1987)1281–1295.

[20]H.B.Keller,Numerical solution of bifurcation and nonlinear eigenvalue problems,in:P.Rabinowitz(Ed.),Applications of Bifurcation Theory,Academic Press,New York 1977,pp.359–384.

[21]A.G.Salinger,N.M.Bou-Rabee,E.A.Burroughs,R.B.Lehoucq,R.P.Pawlowski,L.A.Romero,E.D.Wilkes,LOCA 1.0: “theory and implementation manual.”,Sandia National Laboratories Technical Report,SAND 2002-0396,Sandia National Laboratories,Albuquerque,NM,2002,http://www.cs.sandia.gov/LOCA.

[22]J.N.Shadid,Experimental and Computational Study of the Stability of Natural Convection Flow in an Inclined Enclosure Ph.D.Thesis University of Minnesota,Minneapolis,Minnesota,1987.

[23]R.Seydel,Practical Bifurcation and Stability Analysis,Vol.5,Springer,2010 288–290.

[24]R.Seydel,Numerical computation of branch points in nonlinear equations,Numer.Math.33(1979)339–352.

[25]E.Anderson,Z.Bai,C.Bischof,J.Demmel,J.Dongarra,Lapack Users'Guide:Release 3.0,International Society for Industrial and Applied Mathematics,1999 http://www.netlib.org/lapack/lug/.

[26]M.Lee,C.Dorn,G.A.Meski,M.Morari,Limit cycles in homogeneous azeotropic distillation,Ind.Eng.Chem.Res.38(1999)2021–2027.

[27]T.E.Güttinger,C.Dorn,M.Morari,Experimental study of multiple steady states in homogeneous azeotropic distillation,Ind.Eng.Chem.Res.36(1997)794–802.

[28]C.Dorn,M.Lee,M.Morari,Stability and transient behavior of homogeneous azeotropic distillation,Comput.Chem.Eng.23(1999)S191–S194.