具有时滞的害虫防治模型的分支分析

朱发林，赵维锐

(武汉理工大学 数学系，湖北 武汉 430070)



具有时滞的害虫防治模型的分支分析

朱发林，赵维锐*

(武汉理工大学 数学系，湖北 武汉 430070)

摘要：证明了随着时滞的增大系统在正平衡点处存在Hopf分支，并用庞加莱规范型方法和中心流行定理详细的讨论了Hopf分支的方向及其产生的周期解得稳定性.不仅从理论上分析了系统的动力学性质，而且还作了相应的数值模拟来检验结果.

关键词：生物防治；稳定；Hopf分支；时滞微分方程

在病虫害防治的早期，化学药剂的确有效的控制了病虫害的发生，但是农业长期的使用，给农作物带来的虫害损失却逐年增加.据美国农业部的调查报告，1940年到1978年30多年来，用药量、用药浓度增加了10倍，作物损失从7%反而上升到了17%，虫害没有下降反而上升.这是因为长期使用杀虫剂，已知的1 000多种昆虫产生了原体抗药性，当农药针对性的杀死害虫时，一些害虫的天敌也受到的伤害，使害虫的种群自然控制失控，那些对农药具有抗药性的害虫因主要害虫种群的减少而大量繁殖，这使次要害虫由于缺少竞争而一跃成为主要害虫.长期以来大量使用化学药物的副作用也日渐突出，环境污染、农药残留、害虫抗药性以及害虫的再度猖獗等问题都对化学药剂发出了挑战.害虫治理的目的不是根除害虫，而是维持害虫水平不超过经济临界水平进而获得最佳的经济效益.

随着科学的发展，人们发现具有时滞的微分方程能较确切的反映各种自然现象，因此在工程及种群生物学等领域中越来越多的呈现出使用时滞微分方程来刻画系统的演变.人们用其解释相应系统中平衡点的稳定性，周期解的存在性和稳定性以及分支等动力学行为.许多的生物数学模型被人们分析和研究[1-19].本文研究了三个种群(茶树、害虫和捕食者)之间相互关系的数学模型.A.Maiti et al[1].为了描述生物防治在茶叶生产中的作用提出了如下数学模型：

(1)

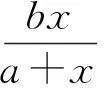
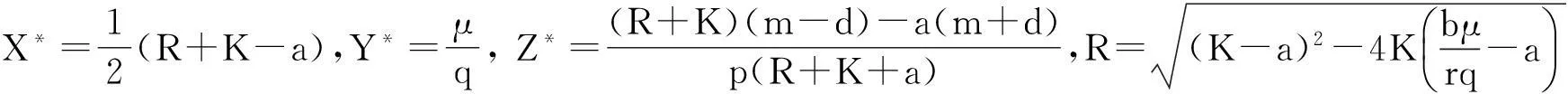
本文结构如下：第1部分，运用庞加莱规范型方法和中心流行定理[2]，分析了当τ=τ*时Hopf分支的方向及其产生的周期解的稳定性.第2部分，取相应的参数值对系统(1)做数值模拟.第3部分分析模拟结果并作进一步展望.

1Hopf分支方向及其产生周期解的稳定性

A.Maitietal[1]证明了当τ=τ*时系统在点E*=(X*,Y*,Z*)处存在Hopf分支.在这一部分，运用庞加莱规范型方法和中心流行定理[2].讨论Hopf分支的方向及其产生的周期解的稳定性.

首先，令 u1=X-X*,u2=Y-Y*,u3=Z-Z*,τ=τ*+μ，在平衡点处线性化，系统(1)可化为如下的泛函微分方程：

(2)

其中：u(t)=(u1(t),u2(t),u3(t))T∈C=C([-1,0],R3) 并且Lμ:C→R3,F:C×R→R3.

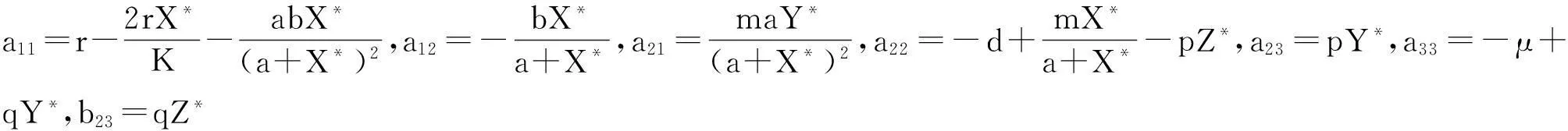
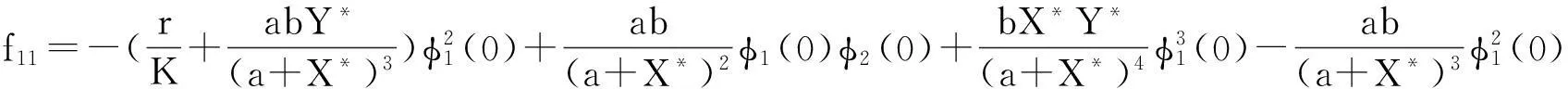
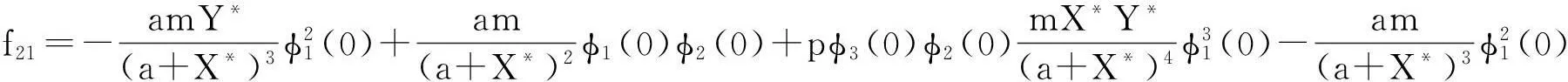
f31=qφ3(0)φ2(-1).

根据Reisz表示定理，对θ∈[-1,0]，存在一个有界变差函数η(θ,μ)，使得：

(3)

对φ∈C([-1,0],R3)，定义：

(4)

下面利用形式伴随理论以及中心流形和规范型理论进行讨论，

对ψ∈C([-1,0],(R3)*)，定义：

(5)

这里，对于ψ∈C([0,1],(R3)*)和φ∈C([-1,0],R3)，适合复向量的双线性形式为:

(6)

它满足<ψ,Aφ>=，其中η(θ)=η(θ,0)，则算子A=A(0)与A*是共轭算子，而±iω0τ*是算子A(0)的特征值，且其它特征值具有严格的负实部，从而±iω0τ*也是算子A*的特征值.下面将分别计算A,A*对应于特征值iω0τ*和-iω0τ*的特征向量，可得到：q(θ)=(1,β,γ)Teiω0τ*θ，q*(s)=D(1,β*,γ*)Teiω0τ*s.

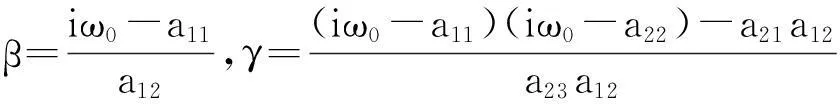
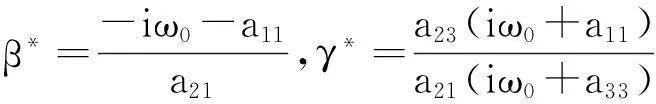
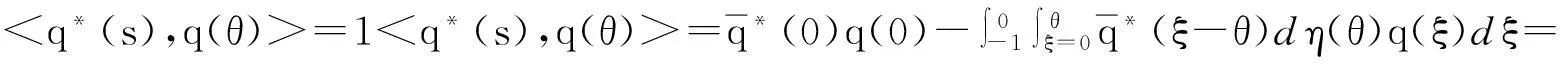
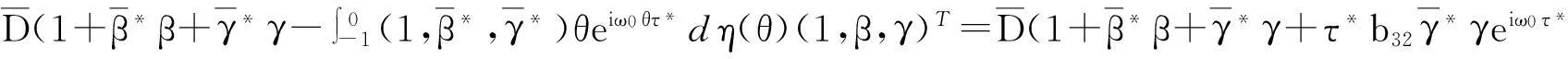
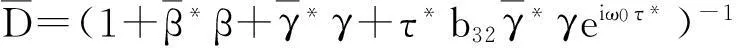
定义1z(t)=,W(t,θ)=ut(θ)-2Re{z(t)q(θ)}，

(7)

(8)

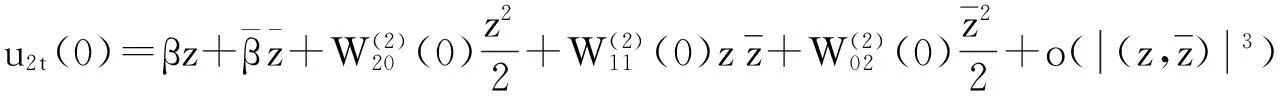
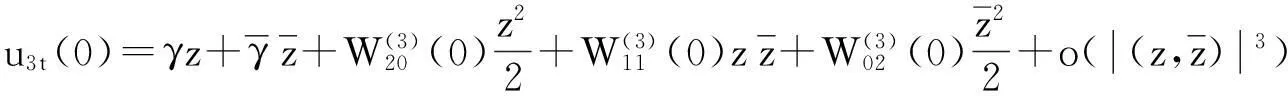
由f(μ,ut)的定义和式(3)有：

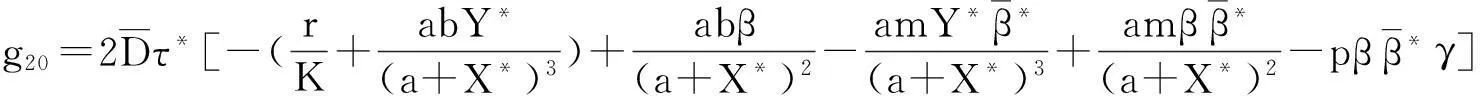
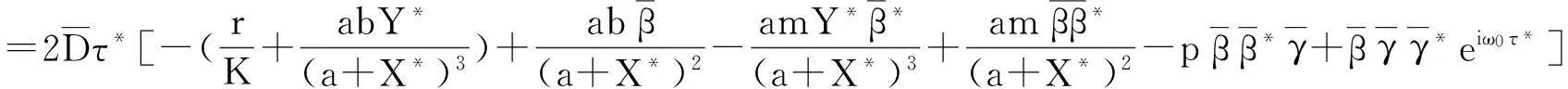
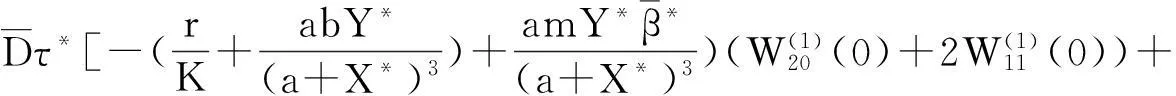
为了确定g21，要计算W20(θ),W11(θ),

单层干燥（6 h）、双层干燥（6 h）、三层干燥（8 h） 的最终样品水分含量分别9.33%，7.77%和8.68%，双层物料最终湿基含水量最低且各层物料最终湿基含水量无显著差异（p＞0.05），物料均匀性最好。

(9)

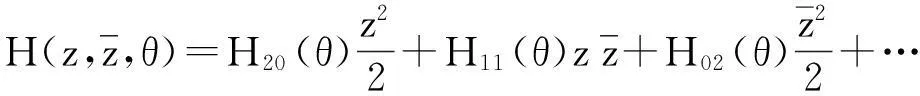
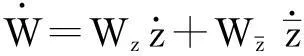
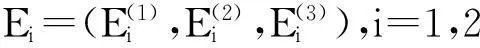
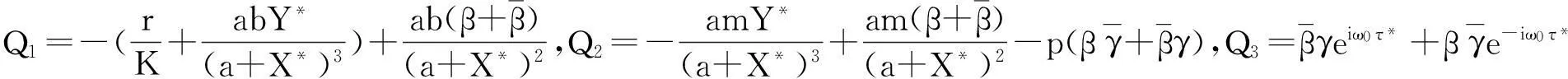
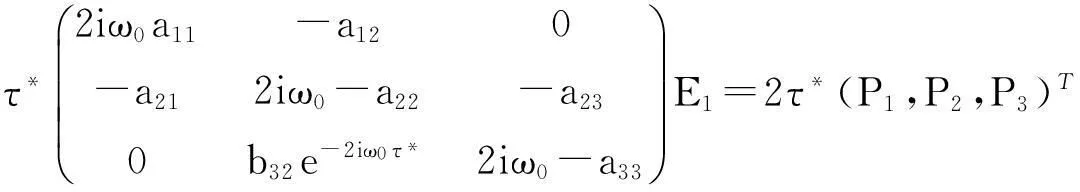
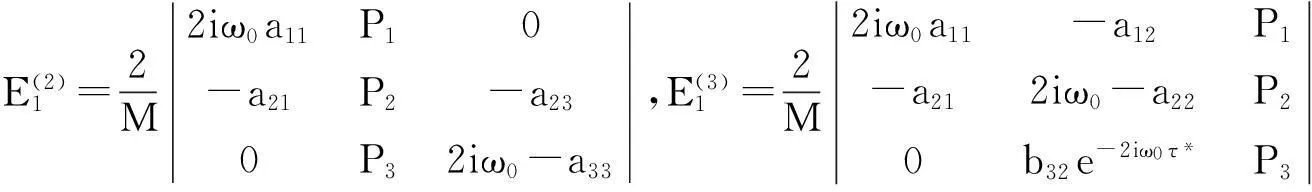
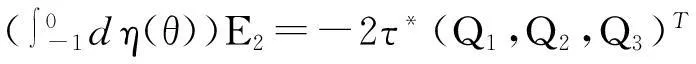
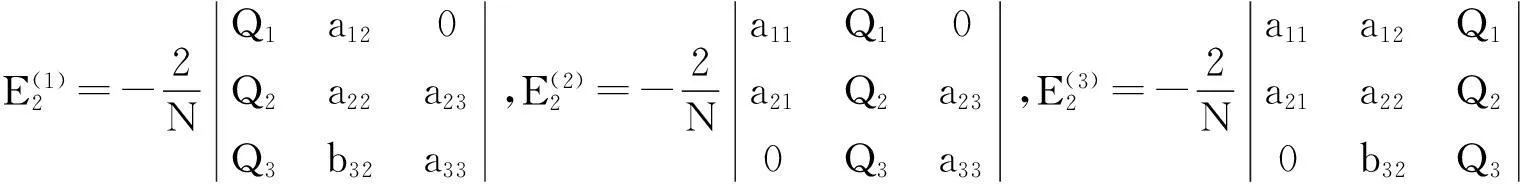
至此，g20,g11,g02,g21全部求得，可以公式化地求得判定Hopf分支性质的关键参数μ2,β2和τ2.

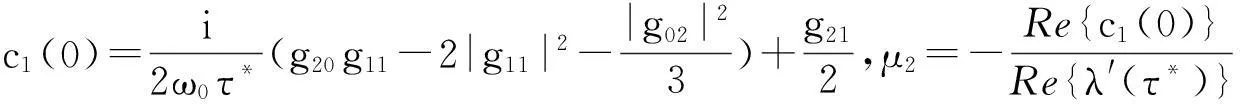
这里μ2决定分支的方向：如果μ2>0(μ2<0)，则系统存在上临界分支(下临界分支).β2决定分支周期解的稳定性：如果β2<0(β2>0)，则分支周期解稳定(不稳定).τ2决定分支的周期：如果τ2>0(τ2<0)，则周期增大(减小).那么有以下结论.

定理1在前面条件下，c1(0)如上，那么有：

1)τ=τ*时系统产生Hopf分支;

2)当Rec1(0)<0时，分支方向向前， 当Rec1(0)>0时，分支方向向后;

3)当Rec1(0)<0时，分支周期解稳定，当Rec1(0)>0时，分支周期解不稳定.

2数值模拟

在这部分用数值模拟来验证前面的分析.取r=1,K=2,a=1,b=1,d=1,m=3,p=1,μ=1,q=1.5且(X(0),Y(0),Z(0))=(3,2,1). 代入算出E*(X*,Y*,Z*)=(1.457,0.667,0.779),τ*=0.115. 所以取τ=0.10<τ*，系统是局部渐近稳定的(见图1～2).当τ(保持其他参数值不变)不断增大到τ=τ*=0.115时稳定性失去.取τ=0.12>τ*，系统不稳定，在E*附近产生分支周期解(见图3～4).

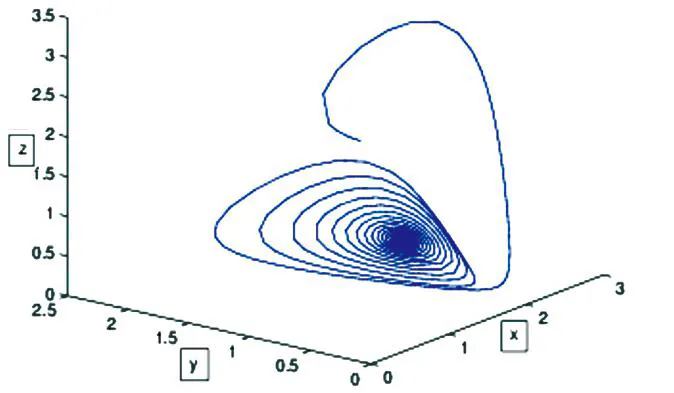
图1　当τ=0<τ*时，系统在E*处局部渐近稳定的相位图Fig．1 Phase portrait of the system showing that E*is locally asymptotically stable

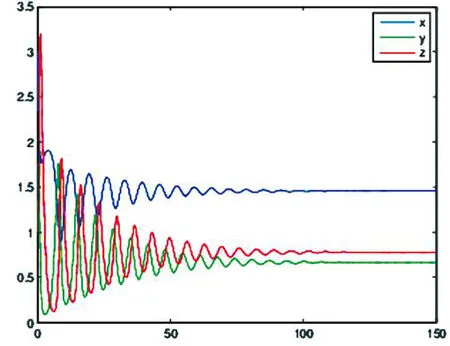
图2　当τ=0.10<τ*时，三种群随着时间的变化趋势Fig．2 Behaviour of the three populations with respect to time

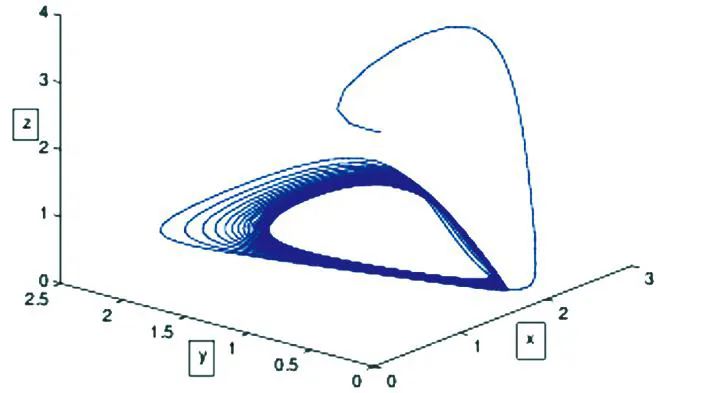
图3　当τ=0.12>τ*时，系统产生周期解的相位图Fig．3 Phase portrait of the system showing a limit cycle which grows out of E*

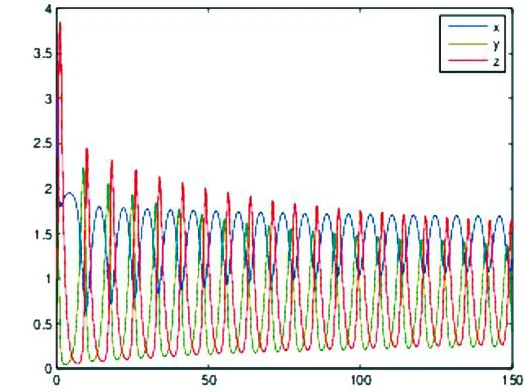
图4　当τ=0.12>τ*时，三种群随时间的变化趋势Fig．4 Oscillation of the three populations respectively in time

3结语

在第2部分用Matlab进行了数值模拟，验证了随着τ的不断增大，系统从稳定变成不稳定，产生了分支，分支周期解是稳定的.这些理论也许在茶叶的害虫防治中有一定的作用，对生态茶叶的种植有一定的指导意义.本文分析了具有一个时滞的害虫防治模型的Hopf分支方向及分支周期解的稳定性.事实上，应该同时还考虑害虫与茶树之间的时滞，即讨论双时滞的害虫防治模型更加符合实际意义.在不久的将来，将进一步研究这一模型的动力学性质，力求得到更多对生态茶叶生产有用的结果.

参考文献:

[1]MAITIi A，PAL A K,SAMANTA G P.Usefulness of Biocontrol of Pests in Tea:A Mathematical Model[J].Mathematical Modelling of Natural Phenomena,2008,3(4):96-113.

[2]HASSARD B D,KAZARINOFF N D,WAN Y H. Theory and Applications of Hopf Bifurcation[M].Cambridge：Cambridge University Press,1981.

[3]SONG Y,HAN Y,ZHANG T.Stability and Hopf bifurcation in a model of gene expression with distributed time delays[J].Applied Mathematics and Computation,2014,243:398-412.

[4]LIAO M,XU C,TANG X.Stability and Hopf bifurcation for a competition and cooperation model of two enterprises with delay[J].Communications in Nonlinear Science and Numerical Simulation,2014,19(10):3845-3856.

[5]ADIMY M,CRAUSTE F,RUAN S.Periodic oscillations in leukopoiesis models with two delays[J].Journal of Theoretical Biology,2007,242(2):288-299.

[6]HUANG J,RUAN S,SONG J.Bifurcations in a predator-prey system of Leslie type with generalized Holling type III functional response[J].Journal of Differential Equations,2014,257(6):1721-1752.

[7]CHENG Z,CAO J.Hopf bifurcation control for delayed complex networks[J].J Franklin Inst,2007,344:846-857.

[8]YU Wenwu,CAO Jinde.Hopf bifurcation and stability of periodic solutions for van der Pol equation with time delay[J].Nonlinear Analysis,2005,62:141-165.

[9]CHENG Zunshui,LI Dehao,CAO Jinde.Stability and Hopf bifurcation of a three-layer neural network model with delays[J].Neurocomputing,2016,175:3 55-370.

[10]ZHANG Yuming,CAO Jinde,XU Wenying.Stability and Hopf bifurcation of a Goodwin model with four different delays[J].Neurocomputing,2015,165:144-151.

[11]XIAO Min,CAO Jinde. Hopf bifurcation and non-hyperbolic equilibrium in a ratio-dependent predator-prey model with linear harvesting rate:Analysis and computation[J].Mathematical and Computer Modelling,2009,50:360-379.

[12]LI X,RUAN S,EI J.Stability and Bifurcation in Delay-Differential Equations with Two-Delays[J].Journal of Mathematical Analysis and Applications,1999,236(2):254-280.

[13]ARIK S.On the global dissipativity of dynamical neural networks with time delays[J].Phys Letters A,2004,326:126-132.

[14]CHEN T P.Convergence of delayed dynamcal systems[J].Neural Processing Letters,1999,10:267-271.

[15]CHEN T P.Global convergence of delayed dynamcal systems[J].IEEE Transactions on Neural Networks,2001,12:1532-1536.

[16]CHEN T P.Global exponential stability of delayed dynamcal systems[J].Neural Networks 2001,14:977-980.

[17]LU W,RONG L,CHEN T P.Global convergence of delayed dynamcal systems[J].International Journal of Neural Systems,2003,13:1-12.

[18]WU C W,HUANGG Y S.A unifying proof of global asymptotical stability of neural networks with delay[J].Proceedings of IEEE International Symposium on Circuits and Systems,Vancouver,Canada,2004,3:65-68.

[19]HALE J K,VERDUYN LUNEL S M.Introduction to Functional Differential Equations[M].New York: Springer,1993.

责任编辑：时凌

Hopf Bifurcation Analysis in a Delayed Mathematical Model of Biocontrol of Pests

ZHU Falin,ZHAO Weirui*

(Department of Mathematics,Wuhan University of Technology，Wuhan 430070,China)

Abstract：In this paper,we prove that the sequence of Hopf bifurcations occurs at the positive equilibrium as the delay increases.Explicit algorithm for determining the direction of the Hopf bifurcations and the stability of the bifurcating periodic solutions are derived,using the theory of normal form and center manifold.The dynamical behaviours are studied both analytically and numerically by computer simnlation.

Key words：biocontrol;stability;Hopf bifurcation;delay differential equations

收稿日期：2015-12-28.

基金项目：湖北省自然科学基金项目(2013CFB347).

作者简介：朱发林(1987- )，男(土家族)，硕士生，主要从事微分方程及其应用研究；*通信作者：赵维锐(1974- )，男(土家族)，博士,教授，主要从事微分方程及其应用研究.

文章编号：1008-8423(2016)01-0005-06

DOI:10.13501/j.cnki.42-1569/n.2016.03.002

中图分类号：O175

文献标志码：A