基于离散小波变换的桥梁结构损伤识别方法
林贝贝,毛 毳,孙 良(. 天津城建大学,天津 300384;. 天津大学,天津 3009)
道路与桥梁
基于离散小波变换的桥梁结构损伤识别方法
林贝贝1,毛 毳1,孙 良2
(1. 天津城建大学,天津 300384;2. 天津大学,天津 300192)
基于小波子带信号的能量曲率变化损伤识别方法,运用ANSYS软件对一简支梁桥在冲击激力下振动响应信号进行数值分析,采用离散小波变换,根据响应信号相对能量的曲率差损伤指标,对具有两处损伤的结构进行损伤位置识别定位.结果表明,在一定条件下,该识别方法识别损伤简单有效,但损伤位置间距对识别效果有一定影响.
损伤;离散小波变换;能量曲率;ANSYS;简支梁;损伤识别
桥梁结构在服役期间会受到各种各样外力作用,不可避免会造成损伤,这些损伤正是导致构件失效甚至造成灾难性事故发生的重要原因.因此,及时、准确地发现桥梁结构的早期损伤,并对其进行针对性加固,具有非常重要的理论意义和社会经济价值.
因桥梁结构复杂,桥梁损伤识别研究具有一定的难度,但众多学者仍探索出了很多不同的研究方法[1],其中由于小波分析[2]对动态信号的奇异性检测具有独特的优势,因此基于小波分析的桥梁损伤识别方法得到了广泛研究[2].如管德清、施立成提出了基于曲率模态小波分析对斜拉桥进行损伤识别的方法[3].孙磊研究了以曲率模态小波系数差作为结构损伤识别指标的适用性和可行性[4].本文基于曲率模态[5]的思想,运用ANSYS软件对一简支梁桥在冲击激力下的振动响应信号进行数值模拟分析,采用离散小波变换,根据信号相对能量的曲率差损伤指标,来验证结构两处损伤位置的识别问题,并研究了损伤位置之间的距离对识别效果的影响.
1 理论分析基础
1.1 MALLAT算法理论介绍
MALLAT算法[6]是离散小波变换的一个重要性突破.它设计简单,运算快捷,它由小波滤波器H、G和h、g对获得的信号进行分解和重构[7],在实际应用中地位非常重要.按离散小波理论,如对响应信号f(t)进行Mallat变换,则每次的分解都会对信号的低频部分在频域上进行二分,每一个频段上下限制都是固定的.假设响应信号f(t)采样频率为FS,根据采样定理得知它的分析频率为FS/2.在经过n次分解之后,信号会被分解到n+1个频段,分别为(0,FS/2,n+1)、(FS/2,n,FS/2,n+1)、…、(FS/4,FS/2).原始响应信号f(t)的Mallat算法分解式子如下
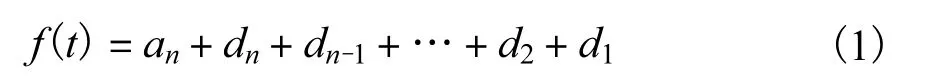
其中:n是分解层次;an是n层分解之后的低频部分;dn,dn-1,…,d2,d1是分解之后各层次的低频成分,即原始信号经过n尺度分解之后的子代信号,an,dn,dn-1,…,d2,d1中包含了信号从低频到高频的不同频带的信息,同时还包含了原始信号的时间信息,因此是对原始信号的时频表示.
本文采用Db4小波基[8]对信号进行小波变换,如图1所示.

图1 三层小波分解示意图
1.2 相对能量曲率差
采用相对能量曲率差作为损伤指标[9],通过对小波变换后的结果进行分析,识别出损伤位置.这种方法指导思想如下:瞬态冲击激励下的结构振动响应是多个模态响应的叠加.根据离散小波变换理论,可选取合适的分解层次,把信号分解至不同频带.假设布设在结构上的传感器个数为n,则各测点的响应信号在经小波分解之后的信号向量X为


式中:T为信号采样时间.
则第k阶振动信号能量向量E为
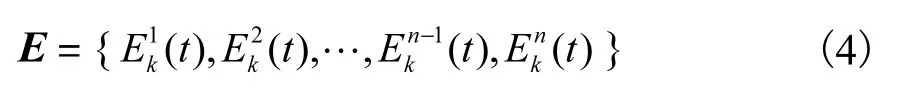
将各个测点同阶振动信号的能量关于全部测点该阶的振动信号能量的总和做归一化处理,结果如下

则信号的相对能量e为
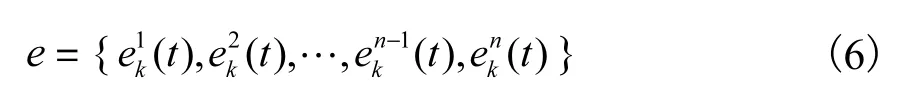
通过计算分析发现,结构损伤前后的相对能量在损伤位置处具有局部奇异性.基于“曲率模态”思想,利用差分法求得信号能量曲率来突显结构局部损伤

由此得出相对能量曲率e′如下
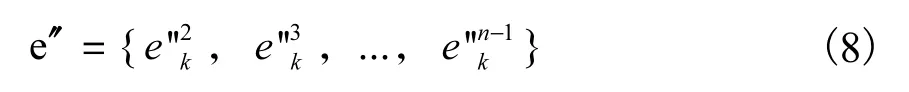
则结构在损伤状态和完好状态下相对能量曲率差为

2 有限元算例
本文采取简支桥梁结构,梁长0.7,m,宽为0.17,m,厚0.006,m,材料弹性模量E=5,GPa,密度ρ=1,210,kg/m3.在桥面对称线上平均设定19个测点(见图2).在梁中轴线上的8号点位置施加100,N的瞬态冲击激励,冲击激励的模拟采用图3所示荷载形式,采样频率为500,Hz,采样时长为2.048,s .损伤模拟采用主梁对称切口,宽为0.002,m,深0.02,m,假设3种损伤状态,损伤工况1:测点4、测点16发生损伤;损伤工况2:测点4、测点13发生损伤;损伤工况3:测点4、测点10发生损伤.采用ANSYS进行瞬态分析,提取桥梁桥面板中轴线上19个节点的加速度响应信号.

图2 简支梁示意图及梁俯视图
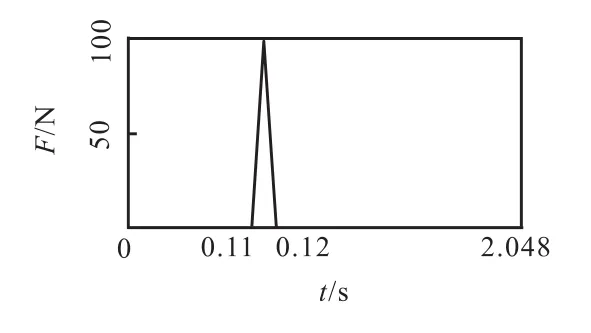
图3 荷载形式
3 信号分析
采用小波变换的方法对结构在完好状态及损伤状态下激励响应信号进行分析.
3.1 结构在完好状态下各测点振动信号小波分析
结构在完好状态下,运用ANSYS软件对图2中简支梁桥在冲击激力下振动响应信号进行数值模拟,得到各个测点的振动加速度响应.通过MATLAB软件分析处理后,得到19个测点的振动响应加速度图像和频谱图.因数据较多,且变化规律相似,故在此以8号测点为例,绘出8号测点加速度时程曲线和加速度信号频谱图,分别如图4-5所示.

图4 结构完好状态下8号测点加速度时程曲线
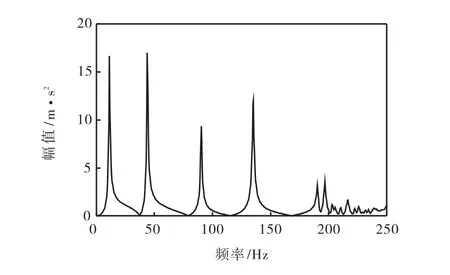
图5 结构完好状态下8号测点加速度信号频谱图
采用Db4小波对8号测点加速度信号进行3层小波分解,得到a3,d3,d2,d1共四个频带信号成分.各个子代的重构信号及其频谱图如图6-7所示.

图6 各子代重构信号
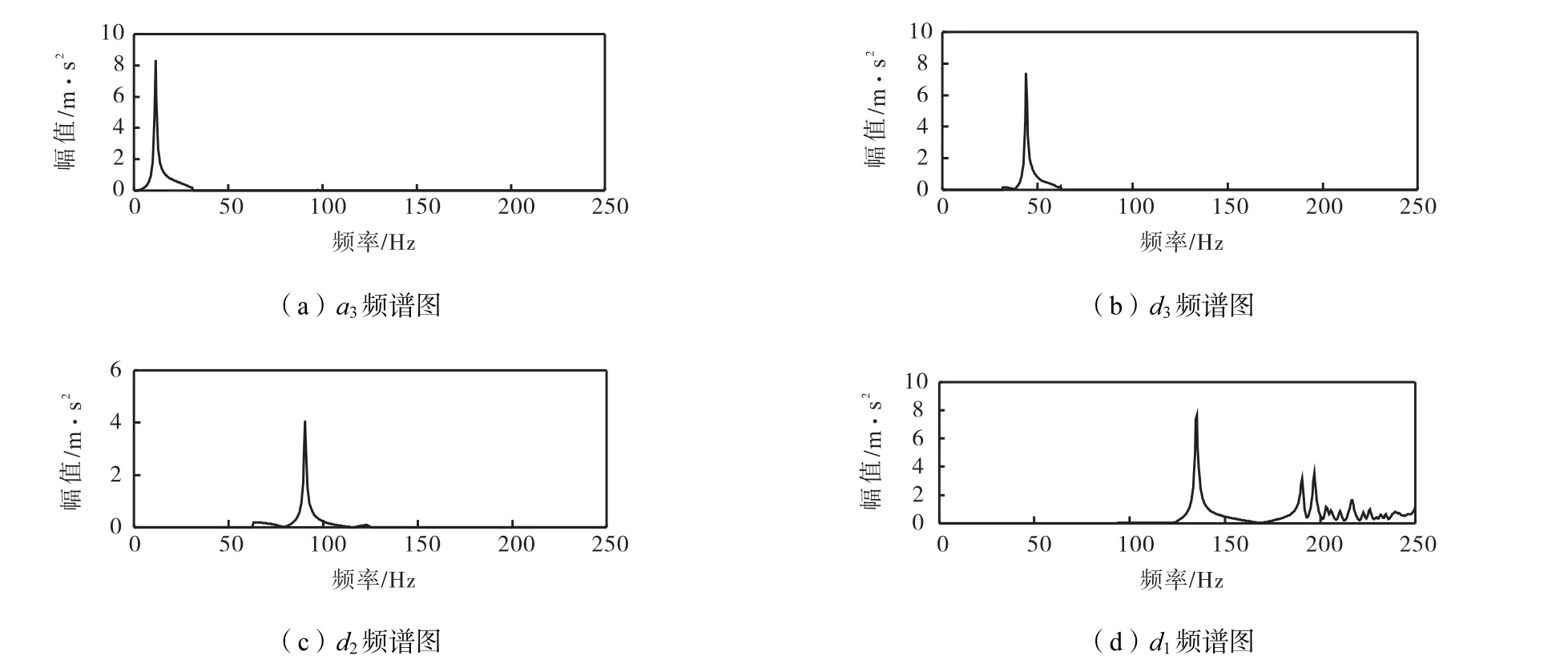
图7 各子代重构信号的频谱图
由此可见,采用这种小波分析,可以使叠加在结构振动响应中前几阶模态响应有效分离.
3.2 结构各阶振动信号相对能量曲率分析
以完好状态和工况1的振动响应做以上小波分析,通过式(2)-(8)计算得到相对能量曲率如图8所示.
由图8可知,结构在损伤前后相对能量曲率分布基本保持吻合状态,只是在结构损伤处附近出现比较敏感的局部奇异性.可见振动响应的相对能量曲率分布对结构局部变化比较敏感,可以反应结构固有的特性.且由图8结果分析可知结构中损伤是存在的,基本上可以对损伤位置进行定位.

图8 各阶振动信号相对能量曲率
3.3 利用相对能量曲率差进行损伤识别
为使上述识别效果更加明显,对结构损伤状态和完好状态下振动信号的相对能量曲率做差得到损伤指标后再进行更准确的分析.对各测点响应进行相对能量曲率分析之后,根据式(9)计算得出完好状态和工况1的前三阶相对能量曲率差,并将三阶曲率差进行叠加得到综合曲率差,如图9所示.根据该指标进行损伤定位.

图9 各阶振动信号相对能量曲率差
由图9可知,损伤的发生使得各测点的相对能量曲率都发生了变化,但是各阶振动信号均是在4号测点和16号测点损伤位置的变化最大.将三阶振动信号相对能量曲率差累加得到综合曲率差如图10a所示,可使损伤位置更加突出.这样,就可以更准确地识别出损伤位置.同理分别得到工况2和工况3的相对能量曲率差,如图10b-10c所示.
由图10b可知,工况2中4号、13号测点综合曲率差最大,可准确识别损伤位置.由图10c可知,工况3中4号、10号综合曲率差最大,也可准确识别出损伤位置.并且由两图对比分析可知,测点距离越远,识别效果越好.

图10 工况1-3综合曲率差
3.4 两处损伤位置距离远近对识别效果的影响
根据测点之间距离由远及近分别定义损伤工况4:测点3、10号发生损伤;损伤工况5:测点3、9号发生损伤;损伤工况6:测点3、7号发生损伤;损伤工况7:测点3、6号损伤.根据以上理论分别作出工况4至工况7的综合曲率差曲线图,如图11所示.

图11 工况4-7综合曲率差
由图11a分析可知,由于3号测点和10号测点距离比较远,可以很清楚地看到,3号测点和10号测点处的综合曲率差比较大,因此可以很准确地识别出损伤位置.同理,由图10b-10d可知,3号测点和9号测点发生损伤时,由于距离比较远,可以准确识别出损伤位置.随着损伤位置之间距离的逼近,3号测点和7号测点发生损伤时,只能观察到3号测点位置处曲率差比较大,而7号测点不能够被识别出来.当损伤位置继续逼近的时候,即3号测点和6号测点位置发生损伤时,两处损伤位置均不能被识别出来.并且结合图10即工况1、2、3,两处损伤位置都距离比较远,尤其是工况1中4号测点和16号测点,距离比较远,识别效果就明显比较好.也就是说结构两处损伤位置的远近,对识别效果的准确性具有一定的影响,损伤位置距离比较远时,识别效果比较准确,随着距离的逼近,识别效果发生变化,当距离达到一定值时,该方法不能准确地识别出损伤位置.
4 结 论
本文通过对瞬态冲击激励下简支梁的数值模拟,得到动态响应,利用二进制离散小波变换对结构的振动响应信号进行分析,根据相对能量曲率差指标对两处损伤位置进行识别定位,结论如下.
(1)该方法可用于结构两处损伤识别,但是损伤识别的有效性受到损伤位置相对距离的影响.
(2)当两处损伤位置距离比较远时,相对能量曲率差可以对简支梁不同位置的多处损伤进行有效识别.
(3)随着两处损伤位置距离的逼近,识别有效性逐渐降低,甚至逼近到一定程度时无法准确识别出损伤位置.
[1] CHEN B,ZANG C. Artificial immune pattern recognition for structure damage classification [J]. Computers & Structures,2009,87(21):1394-1407.
[2] 韩乃杰,张 浩,吴向飞,等. 基于应变模态的桥梁损伤识别方法研究进展[J]. 中外公路,2015,35(1):90-94.
[3] 管德清,施立成. 基于曲率模态小波分析的单塔斜拉桥损伤识别[J]. 建筑科学与工程学报,2010,27(1):21-24.
[4] 孙 磊. 小波分析在桥梁健康监测中的应用研究[D].西安:长安大学,2012:43-73.
[5] 余 竹,夏 禾,Goicolea J M,等. 基于小波包能量曲率差法的桥梁损伤识别试验研究[J]. 振动与冲击,2013,32(5):20-25.
[6] 王帅灵,樊启斌,郑 宏. a尺度正交小波的Mallat算法[J]. 数学杂志,2007,27(6):665-667.
[7] 杨建国. 小波分析及其应用[M]. 北京:机械工业出版社,2005:25-62.
[8] 边 威. 小波基的选取与构造方法讨论[D]. 长春:东北师范大学,2007:19-24.
[9] 相林杰. 基于小波分析的桥梁结构损伤识别方法研究[D]. 天津:天津大学,2013:30-49.
Bridge Structure Damage Identification Methods Based on Discrete Wavelet Transform
LIN Beibei1,MAO Cui1,SUN Liang2
(1.Tianjin Chengjian University,Tianjin 300384,China;2. Tianjin University,Tianjin 300192,China)
Through the approach of damage identification of the change of energy curvature in wavelet subband signal, this paper conducts a data analysis on the vibration response signal of a simply supported beam bridge under impact excitation force by using the ANSYS software. According to the curvature difference damage index of the relative energy of response signal, this research identifies the locations of two damaged structures by using discrete wavelet transform. The research result shows that the damage identification method is simple and effective; however, it is slightly affected by the distance between the damaged locations.
damage;discrete wavelet transform;energy curvature;ANSYS;simply supported beam;damage identification
U446
A
2095-719X(2016)02-0113-06
2015-04-03;
2015-04-17
林贝贝(1988—),女,山东滨洲人,天津城建大学硕士生.

