高强约束混凝土偏压构件受力性态研究
杨德健,张纪刚,常 沙(天津城建大学 土木工程学院,天津 300384)
土木工程
高强约束混凝土偏压构件受力性态研究
杨德健,张纪刚,常 沙
(天津城建大学 土木工程学院,天津 300384)
建立了高强混凝土偏压柱有限元数值模型,分析了箍筋的间距及配箍形式对构件核心区混凝土应变及承载力的影响.结果表明,混凝土的延性和变形受箍筋强度的影响,成较为显著的正相关.高强箍筋在构件破坏阶段具有较高的安全贮备,可对核心区混凝土提供有效约束,但在正常使用状态下箍筋间距和配箍形式对构件延性的影响更大.
高强箍筋;偏心受压;箍筋间距;箍筋形式
我国的《混凝土结构设计规范》(GB 50010—2010)[1]将400,MPa,500,MPa级的钢筋作为主导钢筋,同时将强度等级为C60-C80的高强混凝土列入规范,推荐在结构设计中尽量采用高强材料,提高建筑材料的性价比和使用效率.近年来一些高层建筑和桥梁结构中高强材料得到了使用,但高强纲筋和高强混凝土的用量占建筑材料总体用量的比例仍然很低.叶列平、陆新征[2]指出造成高强材料在实际中应用不足的主要原因是关于高强材料的理论研究过于滞后,随着我国经济的快速发展,实际的需求使得此类研究迅速在各个地区展开,许多学者近些年对此类问题也做了诸多的研究,取得了诸多的成果[3-7].
在实际建筑工程中,很少见到绝对的轴心受压构件,由于材料的不均匀、荷载作用偏离轴心、施工等因素,偏心受压为轴向构件的主要受力方式,结构中多数的柱都是偏心受压构件,此类问题目前研究较少.本文采用有限元数值模拟分析,从混凝土应力应变、混凝土承载力和箍筋应力应变入手,研究高强约束构件在偏心受压荷载的作用下高强箍筋对承载力的影响.
1 偏压构件模型设计
本文采用有限元软件ANSYS进行数值模拟,采用构件1作为验证构件,构件尺寸为150,mm× 150,mm×450,mm,混凝土强度C80,高强箍筋强度为1,120,MPa,直径为6.5,mm,箍筋间距为50,mm,纵筋直径为8,mm,配筋形式如图1所示.
采用分离式模型,混凝土采用SOLID65单元,钢筋采用LINK8三维杆单元,刚性垫块为三维8节点实体SOLID45单元.混凝土采用Willam-Warnke五参数破坏准则和Von Mises屈服准则,选用多线性等向强化模型MISO,其应力-应变关系采用孙军华,干刚征[8]提出的高强箍筋约束高强混凝土的应力-应变曲线表达式,见式(1)至式(4).


式中:k1与k2分别为控制曲线下降段坡度和凸凹的系数.

式中:fc0与fcc分别为非约束与约束混凝土的峰值强度;fle为约束混凝土达到峰值强度时对应的箍筋有效侧向约束力.

式中:εc0为非约束混凝土的峰值应变.
混凝土的MISO模型如图2所示.钢筋采用双线性随动强化模型BIKN.

图1 构件尺寸和截面配筋形式

图2 混凝土的MISO模型
混凝土和钢筋采用分离式模型进行数值建模,首先创建纵筋的模型,按由下而上建模顺序建模,并进行映射网格划分,纵筋单元长度为50,mm.箍筋建模方法同纵筋,单元长度为30,mm,钢筋模型如图3所示.混凝土模型采用自上而下进行建模,并进行单元网格划分,钢筋与混凝土共用节点,模型一端设为固定端,用位移加载方式在另一端施加面荷载,混凝土模型如图4所示.数值分析得出构件1的混凝土应力-应变曲线,并与试验结果进行对比(见图5),两曲线拟合较好,试验和模拟所得混凝土最大应力值分别为69.50,MPa,69.35,MPa,最大应力对应的应变分别为0.003,43,0.003,12,误差均在10%,以内,采用此数值模型对构件分析的结果相对有效.

图3 钢筋有限元模型

图4 混凝土有限元模型

图5 有限元分析结果与试验结果
2 高强约束混凝土柱偏心受压性态分析
2.1 箍筋间距对构件承载力和延性的影响分析
为研究构件承载力和变形受到箍筋间距的影响程度,采用箍筋的间距分为25,mm,50,mm,75,mm三种形式,保持纵向钢筋强度、混凝土强度等级、配筋率和箍筋强度不变,箍筋形式采用普通形式A和复合形式B两种作为对比(见图6),作用荷载分为大偏心和小偏心荷载,构件截面尺寸为300,mm×300,mm,柱高为750,mm,保护层厚度为25,mm.构件的具体参数见表1.

表1 构件设计参数

图6 截面配筋形式
2.1.1 混凝土应力-应变及荷载分析

图7 构件1-3核心区混凝土应力-应变曲线

图8 构件1-3荷载-位移曲线
采用复合箍筋,取构件高中部核心区混凝土单元为研究对象,将构件1-3混凝土单元的应力-应变曲线绘制在同一坐标系中(见图7).由图7可知,混凝土应力-应变曲线峰值随箍筋间距的减小而增大,最大应力分别增加了7.39,MPa和12.83,MPa.故采用复合箍筋时,改变箍筋间距可以有效提高构件的最大应力和应变,提高了构件的变形能力.将荷载-位移曲线绘制在同一坐标系中(见图8),由图8可知,随着箍筋间距的减小,构件混凝土达到最大应力时施加的荷载值不断增加,荷载值依次增加了838.61,kN和614.42,kN,改变箍筋间距可以有效提高构件的承载力.
采用普通形式的箍筋,同样可以得出结论:减小箍筋间距,可以提高构件的变形能力,有效提高构件的承载能力.
2.1.2 箍筋应力分析
取构件高中部受压侧箍筋单元为研究对象,分析构件1-3由于箍筋间距改变对箍筋荷载-应变曲线的影响,将各曲线绘制在同一坐标系中(见图9).各曲线变化相差不大,主要区别在于构件混凝土达到最大应力时,曲线所对应的荷载和应变数值不同,当箍筋间距为25,mm,50,mm,75,mm时,箍筋应变数值最大分别为0.002,8,0.001,9,0.001,4.箍筋间距减小,箍筋的应变数值增大,说明箍筋发挥的约束作用越强.采用小间距的箍筋,箍筋对构件的约束作用好,箍筋的应力值高.通过对箍筋间距分别为25,mm,50,mm,75,mm的构件进行数值分析可得出,减小箍筋间距,实际增大了箍筋对混凝土的约束面积,使箍筋对混凝土的约束加强,三组构件后者与前者相比荷载值分别提高了11.73%,和11.14%,.
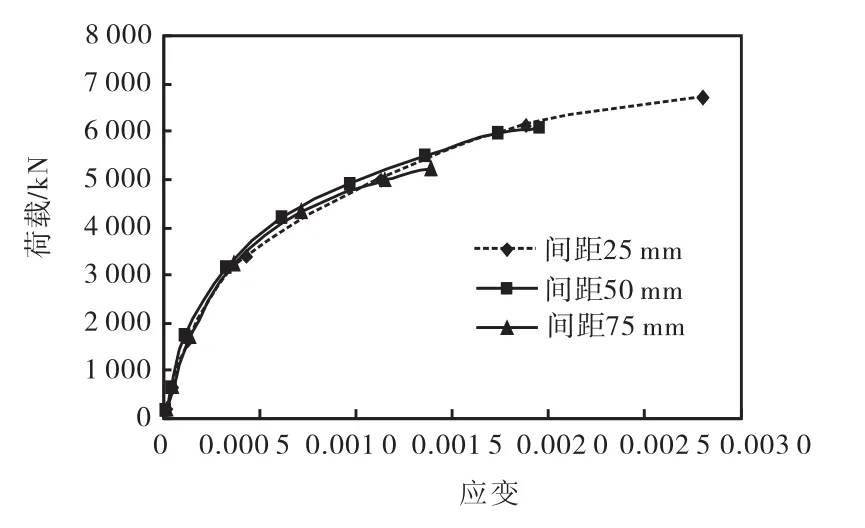
图9 构件1-3荷载-箍筋应变曲线
3根构件在混凝土峰值时高中部截面的应力分布见图10,由图10分析结果表明,在构件到达极限承载力状态时,箍筋应力远未达到其极限强度,表明箍筋尚具有较高的安全储备,能够为进入破坏阶段的混凝土提供有效约束,进而提高构件的延性.此时高强箍筋将发挥普通箍筋不可替代的作用.
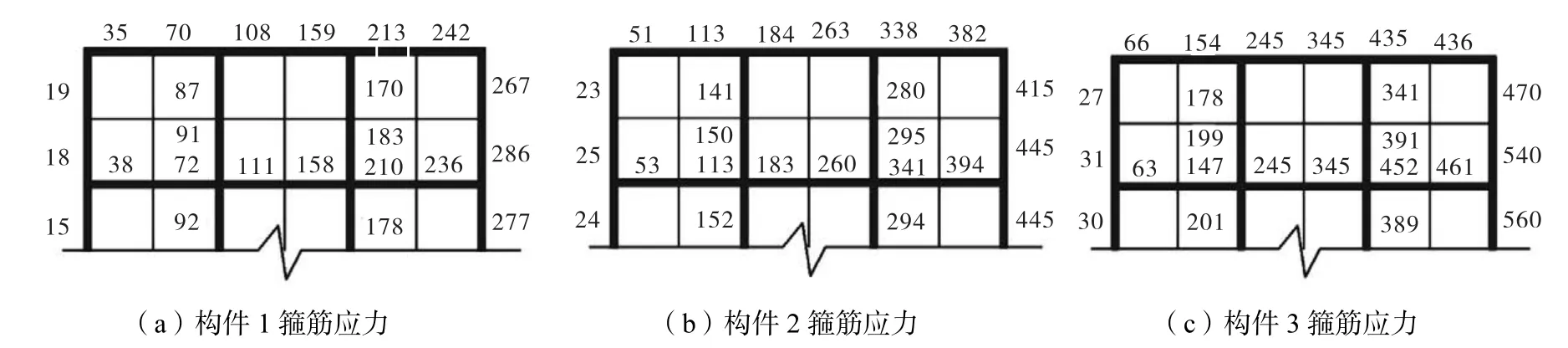
图10 箍筋应力分布
2.2 箍筋形式对构件承载力和延性的影响
研究箍筋形式的变化对构件承载力和变形的影响,采用普通A和复合B两种形式,固定纵向钢筋强度、混凝土强度等级、配筋率和箍筋强度,作用荷载偏心距为30,mm和150,mm两种,分别采用箍筋间距为75,mm和50,mm两种,进行对比分析,构件的具体参数见表2.

表2 构件设计参数
2.2.1 混凝土应力-应变及承载力分析
取构件高中部核心区混凝土单元为研究对象,当为小偏心时,采用复合形式箍筋的构件混凝土单元应力-应变曲线的最大应力和对应的峰值是采用普通形式箍筋构件混凝土最大应力、应变的1.12倍和1.66倍.当为大偏心时,采用复合形式箍筋的构件混凝土单元应力-应变曲线的最大应力和对应的峰值是采用普通形式箍筋构件混凝土最大应力、应变的1.10倍和1.44倍,如图11-12所示.
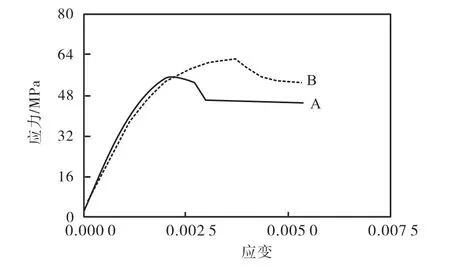
图11 构件1-2核心区混凝土应力-应变

图12 构件3-4混凝土应力-应变
改变箍筋间距,同样使用A、B两种箍筋形式进行验证,所得结果同箍筋间距为75,mm时的结果,即无论是在小偏心荷载还是大偏心荷载作用下,使用复合形式箍筋可以提高构件混凝土的最大应力和峰值应变,增加混凝土的变形能力.

图13 构件1-4荷载-位移曲线
绘制构件1-4荷载-位移曲线(见图13),由图13可知在小偏心荷载作用下,普通形式的箍筋在混凝土达到最大压应力时,施加的荷载值为4,389.51,kN.复合形式的箍筋施加的荷载值为5,239.75,kN,是普通形式箍筋构件荷载值的1.19 倍.将偏心距增加到150,mm,混凝土达到最大压应力时,配置普通形式箍筋和配置复合形式箍筋的构件施加的荷载值分别为1,761.47,kN和2,212.65,kN,后者荷载值是前者的1.26倍.改变箍筋间距,将模拟结果进行对比分析,所得结论和箍筋间距为75,mm时结论一致,即无论是在小偏心荷载还是大偏心荷载作用下,采用复合形式的箍筋能够很好地提高构件的承载能力.
2.2.2 箍筋应力分析
取构件1-4高中部箍筋单元,研究箍筋单元的荷载-应变曲线(见图14).由图14可知,改变箍筋形式对于大、小偏心受压的构件,箍筋的应力变化速率不随箍筋的形式发生改变.但是采用复合形式的箍筋构件中箍筋的应变比采用普通形式箍筋构件的应变大.小偏心受压时,普通形式箍筋和复合形式箍筋构件中箍筋的应变分别为0.000,702和0.001,387,复合形式箍筋是普通形式箍筋应力的1.976倍;大偏心受压时,复合形式箍筋是普通形式箍筋应力的1.679倍;采用复合形式的箍筋,使其接触面积增大,提高了箍筋对混凝土的约束能力.

图14 构件1-4箍筋荷载-应变曲线
3 结 论
本文分析了配置高强箍筋的高强混凝土偏压柱受力性态及影响因素,得出如下主要结论.
(1) 适当的缩短箍筋间的间距是提高承载力的有效手段.对于间距为25,mm,50,mm,75,mm的三种形式,以上构件间距每缩短25,mm,承载力将会有11%,左右的提高,其效果变换明显.
(2) 相比于箍筋间距,改变箍筋形式使箍筋与核心区混凝土有了更充分的接触,大大增加了箍筋与混凝土的咬合面积,在不改变箍筋位置的前提下大幅度提高了构件性能.如本文A、B两种形式,B种复合形式构件其荷载提高20%,左右,箍筋应力提升60%,以上,能够充分发挥箍筋的约束能力.
(3) 高强箍筋对构件约束的影响主要通过箍筋间距和箍筋形式,而高强箍筋的强度对构件的约束,只能在构件倒塌破坏时有明显体现.
[1] 混凝土结构设计规范:GB50010—2010[S].
[2] 叶列平,陆新征. 高强高性能工程结构材料与现代工程结构及其设计理论的发展[C]// 第一届结构工程新进展国际论坛文集.北京:中国建筑工业出版社,2006:208-250.
[3] 郭献忠. 区域约束高强混凝土轴心受压短柱的非线性分析研究[D]. 贵州:贵州大学,2006:64-65.
[4] 史庆轩,杨 坤,白力更,等. 高强箍筋约束高强混凝土柱抗震性能试验研究[J]. 土木工程学报,2011,44(12):9-17.
[5] 赵 东. 高强箍筋约束混凝土偏心受压构件试验及非线性分析[D]. 西安:西安建筑大学,2008:53-54. [6] 李 坤. 不同强度等级混凝土梁柱节点承载力实验研究[D]. 合肥:合肥工业大学,2004:47-48.
[7] 史庆轩,杨 坤,刘维亚,等. 高强箍筋约束高强混凝土轴心受压力学性能试验研究[J]. 工程力学,2012,29(1):141-149.
[8] 孙军华,干 钢. 高强约束混凝土梁截面的延性计算[J]. 工业建筑,2001,31(12):43-46.
Research on Stress Performance of Confined High-strength Concrete Eccentric Compression Member
YANG Dejian,ZHANG Jigang,CHANG Sha
(School of Civil Engineering,TCU,Tianjin 300384,China)
A high strength concrete column bias finite element numerical model is established, and the influence of the reinforcement spacing of stirrups and form on the strain and bearing capacity of core concrete of components is analyzed. The results show that the ductility and deformation of the concrete are influenced by the strength of the stirrup, and are positively correlated. With high security reserves, high-strength stirrup in component failure stage can improve the core concrete effective constraint, but under the normal operation condition the reinforcement and stirrup spacing form have a greater influence on component ductility.
high-strength stirrup;eccentric compression;stirrup spacing;stirrup form
材料科学与工程
TU375
A
2095-719X(2016)02-0104-05
2015-04-23;
2015-05-06
杨德健(1962—),男,天津人,天津城建大学教授,博士.

