基于紧凑度和调度处理的粒子群优化算法*
周 丹,葛洪伟+,苏树智,袁运浩
基于紧凑度和调度处理的粒子群优化算法*
周丹1,2,葛洪伟1,2+,苏树智1,袁运浩1
1.江南大学物联网工程学院,江苏无锡214122
2.江南大学轻工过程先进控制教育部重点实验室,江苏无锡214122
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(05)-0742-09
http://www.ceaj.org Tel: +86-10-89056056
* The National Natural Science Foundation of China under Grant No. 61402203 (国家自然科学基金); the Research Innovation Program for College Graduates of Jiangsu Province under Grant No. KYLX15_1169 (江苏省普通高校研究生科研创新计划项目).
Received 2015-06,Accepted 2015-08.
CNKI网络优先出版: 2015-08-28, http://www.cnki.net/kcms/detail/11.5602.TP.20150828.1622.012.htm l
ZHOU Dan, GE Hongwei, SU Shuzhi, et al. Particle compaction and scheduling based particle swarm optim ization. Journal of Frontiersof Computer Scienceand Technology, 2016, 10(5):742-750.
摘要:针对标准粒子群优化算法存在收敛速度慢和难以跳出局部最优等问题,提出了一种基于紧凑度和调
度处理的粒子群优化算法。给出了粒子紧凑度和调度处理的概念和方法,通过动态评价粒子群中各粒子间的紧凑程度,从而确定调度的粒子,进而对其进行调度处理,避免粒子陷入局部最优。对11个常见的标准函数进行测试,并与标准粒子群算法和其他改进算法进行对比,实验结果表明,基于紧凑度和调度处理的粒子群优化算法具有较高的寻优精度和较快的收敛速度。
关键词:粒子群优化算法;局部最优;紧凑度;调度处理;寻优精度;收敛速度
1 引言
粒子群优化算法(particle swarm optim ization,PSO)是Kennedy等人受到飞鸟集群活动的规律性启发而提出的一种智能优化算法。与其他进化算法相比,它容易实现,参数较少,具有较低的时间和空间复杂度,已在科学和工程领域得到了广泛的研究和应用。但是,PSO算法在寻优过程中依然存在着收敛速度慢,易陷入局部最优的缺陷。近年来,相关学者对此提出了很多改进方法,如在基本PSO中引入惯性权值[1-3]、压缩因子[4]以及健康度[5-6]的概念等,这类改进算法虽然能在一定程度上改善PSO的搜索性能,提高算法的收敛速度,但是在处理一些多峰函数时,仍存在易陷入局部最优的问题。为了增强粒子的全局探索能力,在有限规模内保持粒子群的多样性,避免种群陷入局部最优,学者们在基本PSO中引入了交叉机制[7]、自适应变异机制[8-12]等方法,但却降低了种群的收敛速度。鉴于单一的智能算法在实际应用中面临各自的问题,相互之间的促进与补充便成为可行的改进途径,因此学者们提出混合各种启发式算法的改进思路,如在PSO中引入蚁群算法的信息素机制[13]、极值优化[14]、爬山策略[15]、人工鱼群思想[16]等,但就总体而言,这些算法仍然存在收敛速度慢和易陷入局部最优等缺陷。
通过分析可以看出,粒子群算法存在的主要问题是:(1)对当前全局最优值的追逐力度不够,导致收敛速度不够快;(2)算法迭代中后期,粒子的多样性不够,导致搜索范围不够大,算法全局探索能力较弱,且没有有效的机制使粒子跳出局部最优,最终导致算法收敛精度不够高。为了解决此问题,本文引入了紧凑度和调度处理的概念,提出了基于紧凑度和调度处理的粒子群优化算法(particle compaction and scheduling based particle swarm optimization,PCSPSO)。本文算法通过动态计算粒子间的紧凑度来确定调度粒子,进而对调度粒子进行调度处理,扩大粒子的搜索范围,增强算法的全局探索能力;同时在调度过程中,全局最优值Pg的引导增强了算法的收敛速度。
2 标准粒子群优化算法
标准粒子群优化算法的数学描述为:在D维的搜索空间中,每一个粒子都被看成空间中的一个点,不妨设空间中共有m个粒子,则第i个粒子的空间位置为Xi=[xi1,xi2,…,xiD],其速度为Vi=[vi1,vi2,…,viD],其所经历的最优位置即个体历史最优位置Pi=[pi1,pi2,…,piD],其中i=1,2,…,m。所有粒子经历过的最优位置即全局最优位置Pg=[pg1,pg2,…,pgD]。粒子的位置和速度更新公式分别为:
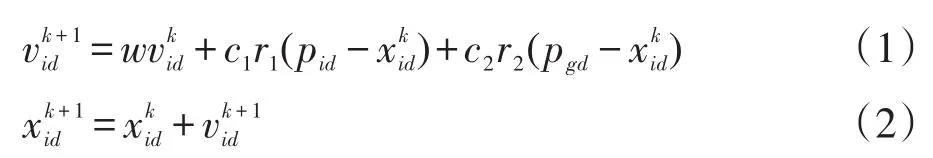
其中,w为惯性权值;c1和c2是加速系数;r1和r2均为[0,1]之间的随机数。
3 相关问题描述
定义1(σ2)[11]设粒子群的粒子数目为m,f(Xi)为第i个粒子的适应值,favg(X)为粒子群目前的平均适应度,σ2为粒子群当前的适应度方差:

定义2(I(X(t)))[17]设粒子群中粒子数目为m,粒子维数为D,粒子群的位置多样性I(X(t))定义如下:

4 基于紧凑度和调度处理的粒子群算法
4.1紧凑度
定理1如果粒子群算法陷入早熟收敛或者达到全局收敛,则群体适应度方差σ2等于0。
证明令φ1=c1r1,φ2=c2r2,综合式(1)、(2)得:


其中,Pi为个体最优值位置;Pg为全局最优值的位置。
如果粒子群算法出现早熟收敛或者达到全局收敛,则个体最优值、全局最优值不再发生变化;此时需考虑当算法出现早熟收敛或者全局收敛时,随机量φ1、φ2对粒子的影响,由于φ1=c1r1,φ2=c2r2,r1、r2服从均匀分布,为了简化处理,利用其期望值进行观察,即:


由定理1可知,当粒子群出现早熟或全局收敛时,群体的适应度方差等于0,此时种群的全局探索能力较弱,为了避免种群陷入局部最优,本文提出了紧凑度的概念,即当两粒子间的适应度差值在一个门限值范围内时,就认定此时两粒子处于紧凑状态。虽然处于紧凑状态的粒子能够加强局部搜索能力,但却降低了粒子群的全局探索能力,使种群更容易出现早熟收敛。因此,本文根据经验值设定具体的紧凑度阈值,当相邻两粒子间的适应度差值小于此阈值时,就可认定两粒子已达到了紧凑状态,否则,两粒子未达到紧凑状态。
4.2粒子调度处理的方法
对粒子进行调度处理的主要目标是为了在提高算法寻优精度的同时,加快算法的收敛速度。为了提高算法的寻优精度,本文利用式(9)、(10)对粒子的历史最优位置Pi、当前位置Xi进行处理,从而改变粒子的运动轨迹,扩大粒子群的搜索范围;由于有全局最优位置Pg的参与和调度系数c3的控制,调度粒子能够在Pg周围进行搜索,提高算法的寻优精度,同时使得粒子搜索到优于已有Pg的概率大大提高,加快算法的收敛速度。

其中,r3,r4∈[0,1],k,h∈{1,2,…,m},d∈{1,2,…,D},且k、h均为随机值,这些参数的随机性保证了算法具有很强的探索能力;c3为调度系数,用于控制调度粒子对Pg的跟随程度,在提高算法寻优精度的同时尽量避免陷入局部最优。
控制种群位置多样性是提高算法全局探索能力的重要手段之一,因此PCS-PSO算法在处理调度粒子时,通过以一定的小概率p1随机改变粒子的当前位置而不受Pg的限制,提高算法的全局探索能力。此时虽然会在一定程度上减慢整个种群的收敛速度,但通过小概率p1的控制,可以有效地协调收敛速度与全局探索力度,使种群在快速搜索全局最优值的同时,能够扩大搜索范围,增强算法的全局探索能力。具体做法如式(11)所示:
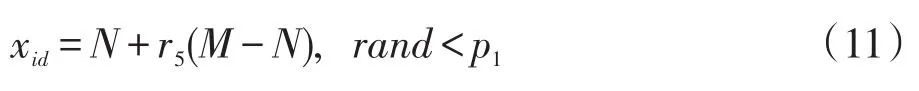
4.3算法描述
针对标准粒子群算法在迭代初期收敛速度慢,而在迭代后期又存在不易跳出局部最优的缺陷,本文提出了基于紧凑度和调度处理的粒子群算法(PCS-PSO)。在PCS-PSO算法中,首先需根据具体问题确定一个合适的紧凑度阈值Hth,然后在种群每一次迭代结束后,根据紧凑度正确选择调度粒子,并对其进行调度。具体做法为:在粒子群每一次更新结束后,按粒子的适应度值对粒子进行排序,若相邻两粒子处于紧凑状态,则对前一粒子进行调度,直到算法结束。
4.4算法步骤
步骤1随机初始化粒子群中各粒子的速度和位置:

步骤2更新粒子群中所有粒子的速度和位置:

步骤3将粒子按当前适应度值的大小排序。
步骤4若相邻两粒子处于紧凑状态,则对前一粒子进行如下调度处理:
若产生的随机数rand 步骤5若粒子的当前适应度值优于目前的全局最优值,则更新粒子群Pg。 步骤6判断是否满足结束条件,若不满足,跳转至步骤2;否则,算法结束。 5.1测试函数 本文在实验中选取了Sphere、Rosenbrock、Penalized、Levy、Griewank、Rastrigin、NC- Rastrigin、Ackley、Cigar、Ellipse、Quadric这11个变量维数可变的常用测试函数(见表1)。在进行参数选择实验时,仅用了F1~F4;在与其他算法(PSO、HPSO[5]、APSO[12])进行对比时,所有函数均会被测试。此外,为了保证实验数据的公平有效,本文具体做法如下:(1)在每次运行各种算法之前,生成一组初始值并初始化粒子,从而消除因初始值不同而导致的差异;(2)每次实验均将各算法反复运行20次,最后对其进行统计,从而消除因算法随机性导致的差异。 Table 1 Test functions表1 测试函数 5.2参数的选择实验 在实验中适应度阈值根据经验值取Hth=100,下面对PCS-PSO算法中的参数c3、p1进行实验和分析。为了确定调度处理时调度系数c3的最佳值,设定粒子维度D=30,小概率p1=0.05,粒子数目m=30,最大迭代次数itmax=3 000,对c3取值分别为0.1、0.3、0.4、0.5、0.6、0.7、0.9、1.1时进行了测试,实验结果如表2所示。其中Mean表示20次实验中最优解的平均值,反应了解的质量;Std表示解的方差,反应了算法的稳定性和鲁棒性。 从表2中可以看出,当调度系数c3的取值为0.5时,算法的寻优精度最高,性能最优。调度系数c3体现了调度粒子对全局最优值Pg的依赖程度。从表中数据分析可知,当c3较大时,会导致调度粒子过度依赖Pg而出现寻优精度不高的现象;当c3较小时,会出现粒子对最优位置Pg的利用力度不够,在3 000次迭代内寻优精度不够高,这在F2、F3、F4中体现得较为明显,即当c3≤0.5时,算法在给定迭代次数内的寻优精度随着c3的增加而提高。 下面继续研究小概率p1对算法的影响。对p1分别取0、0.01、0.03、0.05、0.07、0.10、0.20进行测试,此时调度系数取最佳值,即c3=0.5,其他参数的设置同上,实验结果见表3。 Table 2 Influence of different c3on PCS-PSO表2 不同c3对PCS-PSO算法的影响 Table 3 Influence of different p1on PCS-PSO表3 不同小概率对PCS-PSO算法的影响 从表3中可以看出,当小概率p1=0.05时,算法的寻优精度最高,性能最优。这一点充分体现了粒子群在寻优过程中,小概率扰动对提高算法收敛精度有一定的贡献,而以较大概率进行扰动又会导致对当前全局最优值的追逐力度不够,降低算法的收敛速度。这一点在函数F2、F3、F4中表现得较为明显,即当p1≤0.05,寻优精度随着p1的增加而提高;而当p1>0.50时,寻优精度却随着p1的增加而降低。 5.3性能测试实验与分析 为了验证本文算法(PCS-PSO)的性能,将PCSPSO算法与标准PSO、收敛速度快且寻优能力相对较好的HPSO[5]、寻优能力强且不易陷入局部的APSO[12]进行了对比。各算法的详细参数(HPSO、APSO的参数设置方案分别源自文献[5,12])如表4所示,其中粒子维数D=30,粒子个数m=30。实验结果统计表如表5所示,其中Best、Worst、Mean、Std、S.R.分别表示各算法在20次独立实验过程中的最好值、最坏值、平均值、适应度方差和达到指定精度(1.00E-04)的百分比。 Table 4 Setting parameters for algorithms表4 各算法参数设置 从表5可以看出,PCS-PSO算法较其他对比算法表现出了良好的收敛速度和收敛精度,在F2、F3和F4中表现得尤为突出。F2(Rosenbrock)是非凸的病态函数,常用于考察算法的执行效率;F3(Penalized)、F4(Levy)均为多峰函数,用于考察算法跳出局部最优的能力。APSO算法在多峰函数F4、F5、F6、F7、F8中寻优精度不够高;HPSO算法在多峰函数F3、F4中寻优能力较弱;PCS-PSO算法在上述所有多峰函数上的寻优精度较高,从而表明了本文算法PCS-PSO减轻了局部极值现象。为了进一步展现PCS-PSO算法在寻优速度上的优势,表6给出了各算法达到指定精度(1.00E-04)所花费的时间。运行环境为:CPU Intel i5-3470,主频3.2 GHz,内存4.0 GB,64位Win7系统;实验在Matlab 2010 b软件上运行。统计结果为20次重复实验的平均值,若200 000次迭代后还未达到该精度,则用“—”表示。此外,图1、图2分别给出了粒子的收敛曲线和位置多样性变化图,由于篇幅有限,本文列举了具有代表性的6个测试函数的收敛曲线图和3个测试函数的位置多样性变化图,在其他测试函数上也有相似的性能。 Table 6 Running time of algorithms表6 各算法达到指定精度的运行时间 Fig.1 Convergence curve图1 收敛曲线 Fig.2 Position variety图2 位置多样性 从图1中可以看出,PCS-PSO算法具有较快的收敛速度,特别是在Sphere和Cigar函数中表现得尤为明显,只需较少的迭代次数就能找到全局最优解。从图2中可以看出,在迭代初期,PCS-PSO算法中粒子多样性相对较低,使得种群的搜索范围相对较小,从而使算法具有相对较强的局部搜索能力,加快种群的收敛速度;在迭代后期,PCS-PSO算法中粒子多样性相对较高,有利于粒子在较大范围内进行搜索,增强粒子群的全局探索能力,提高算法收敛精度。纵观整个迭代过程,PCS-PSO算法中粒子群的位置多样性I(X(t))较为稳定,有利于平衡种群的局部搜索和全局探索能力。通过对表5和图1的数据进行分析易知,PCS-PSO算法在收敛速度和寻优精度上明显优于其他对比算法。 由于标准粒子群优化算法在寻优时存在收敛速度慢和易陷入局部最优等问题,本文给出了紧凑度的概念和相应的调度处理方法,提出了基于紧凑度和调度处理的粒子群算法,在种群每一次迭代更新结束后,通过统计粒子间的紧凑程度,选择合适的粒子对其进行调度,保证了种群的搜索范围,避免种群多样性的缺失,具体的调度策略使算法在整个寻优过程中能够有效地平衡种群的局部搜索能力和全局探索能力。仿真实验结果表明,本文提出的基于紧凑度和调度处理的粒子群算法在收敛速度和寻优精度上具有良好的性能。 References: [1] Shi Yuhui, Eberhart R. A modified particle swarm optimizer [C]//Proceedings of the 1998 IEEE International Conference on Evolutionary Computation, Anchorage, USA, May 4-9, 1998. Piscataway, USA: IEEE, 1998: 69-73. [2] Shi Yuhui, Eberhart R C. Parameter selection in particle swarm optimization[C]//LNCS 1447: Proceedings of the 7th International Conference on Evolutionary Programm ing, San Diego, USA, Mar 25- 27, 1998. Berlin, Heidelberg: Springer, 1998: 591-600. [3] Chatterjee A, Siarry P Nonlinear inertia weight variation for dynamic adaptation in particle swarm optim ization[J]. Computers & Operations Research, 2006, 33(3): 859-871. [4] Clerc M, Kennedy J. The particle swarm-explosion, stability and convergence in a multi-dimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6 (1): 58-73. [5] Jin Qibing, Wang Kewen, Zhao Zhenxing, et al. HPSO algorithm w ith high speed convergent based on particle health degree[J]. Applied Mathematics & Information Sciences, 2014, 8(4): 1809-1821. [6] Jin Qibing, Zhao Zhenxing, Su Xiaojing, et al. PSO algorithm with high speed convergence based on particle health[J]. CIESC Journal, 2011, 62(8): 2328-2333. [7] Angeline P J. Evolutionary optimization versus particle swarm optim ization: philosophy and performance differences[C]//LNCS 1447: Proceedings of the 7th International Conference on Evolutionary Programming, San Diego, USA, Mar25-27,1998.Berlin,Heidelberg:Springer,1998:601-610. [8] Zhang Dingxue, Liao Ruiquan. Adaptive particle swarm optimization algorithm based on population velocity[J]. Control and Decision, 2009, 24(8):1257-1260. [9] Zhu Haimei, Wu Yongping. A PSO algorithm w ith high speed convergence[J]. Control and Decision, 2010, 25(1): 20-24. [10] Ren Zihui, Wang Jian. Accelerate convergence particle swarm optimization algorithm[J]. Control and Decision, 2011, 26(2): 201-206. [11] Lv Zhensu, Hou Zhirong. Particle swarm optimization w ith adaptive mutation[J]. ACTA Electronica Sinica, 2004, 32(3): 416-420. [12] Zhan Zhihui, Zhang Jun, Li Yun, et al. Adaptive particle swarm optim ization[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2009, 39(6): 1362-1381. [13] Shelokar P S, Siarry P, Jayaraman V K, et al. Particle swarm and ant colony algorithms hybridized for improved continuous optim ization[J]. Applied Mathematics and Computation, 2007, 188(1): 129-142. [14] Chen M inrong, Li Xia, Zhang Xi, et al. A novel particle swarm optimizer hybridized w ith extremal optimization[J]. Applied Soft Computing, 2010, 10(2): 367-373. [15] Wu Yonghua, Peng Yong, Wang Gang. Hybrid particle swarm optimization algorithm based on colony mountainclimbing strategy[J]. Computer Engineering and Applications, 2014, 50(1): 45-48. [16] Yao Xiangguang, Zhou Yongquan, Li Yongmei. Hybrid algorithm w ith artificial fish swarm algorithm and PSO[J]. Application Research of Computer, 2010, 27(6): 2084-2086. [17] Shen Yuanxia, Wang Guoyin, Zeng Chuanhua. Study on the relationship between population diversity and learning parameters in particle swarm optim ization[J]. ACTA Electronica Sinica, 2011, 39(6):1238-1244. [18] Li Ning, Sun Debao, Zou Tong, et al.An analysis for a particleƳs trajectory of PSO based on difference equation[J]. Chinese Journal of Computers, 2006, 29(11): 2052-2061. 附中文参考文献: [6]靳其兵,赵振兴,苏晓静,等.基于粒子健康度的快速收敛粒子群优化算法[J].化工学报, 2011, 62(8): 2328-2333. [8]张顶学,廖锐全.一种基于种群速度的自适应粒子群算法[J].控制与决策, 2009, 24(8): 1257-1260. [9]朱海梅,吴永萍.一种高速收敛粒子群优化算法[J].控制与决策, 2010, 25(1): 20-24. [10]任子晖,王坚.加速收敛的粒子群优化算法[J].控制与决策, 2011, 26(2): 201-206. [11]吕振肃,侯志荣.自适应变异的粒子群优化算法[J].电子学报, 2004, 32(3): 416-420. [15]吴永华,彭勇,汪刚.基于群体爬山策略的混合粒子群优化算法[J].计算机工程与应用, 2014, 50(1): 45-48. [16]姚祥光,周永权,李咏梅.人工鱼群与微粒群混合优化算法[J].计算机应用研究, 2010, 27(6): 2084-2086. [17]申元霞,王国胤,曾传华. PSO模型种群多样性与学习参数的关系研究[J].电子学报, 2011, 39(6): 1238-1244. [18]李宁,孙德宝,邹彤,等.基于差分方程的PSO算法粒子运动轨迹分析[J].计算机学报, 2006, 29(11): 2052-2061. ZHOU Dan was born in 1989. She is an M.S. candidate at Jiangnan University, and the member of CCF. Her research interests include artificial intelligence and pattern recognition. 周丹(1989—),女,湖北荆州人,江南大学硕士研究生,CCF会员,主要研究领域为人工智能,模式识别。 GE Hongwei was born in 1967. He received the M.S. degree in computer science from Nanjing University of Aeronautics and Astronautics in 1992 and the Ph.D. degree in control engineering from Jiangnan University in 2008. Now he is a professor and Ph.D. supervisor at School of Internet of Things Engineering, Jiangnan University. His research interests include artificial intelligence and pattern recognition, machine learning, image processing and analysis, etc. 葛洪伟(1967—),男,江苏无锡人,1992年于南京航空航天大学计算机系获得硕士学位,2008年于江南大学信息学院获得博士学位,现为江南大学物联网工程学院教授、博士生导师,主要研究领域为人工智能与模式识别,机器学习,图像处理与分析等。在国际权威期刊、会议和国内核心期刊上发表论文70多篇,主持和承担了国家自然科学基金等国家级项目和省部级项目近20项,获省部级科技进步奖多项。 SU Shuzhi was born in 1987. He is a Ph.D. candidate at Jiangnan University. His research interests include pattern recognition and machine learning. 苏树智(1987—),男,山东泰安人,江南大学博士研究生,主要研究领域为模式识别,机器学习。 YUAN Yunhao was born in 1983. He received the Ph.D. degree from Nanjing University of Science and Technology in 2013. Now he is an associate professor at Jiangnan University. His research interests include pattern recognition and machine learning. 袁运浩(1983—),男,江苏徐州人,2013年于南京理工大学获得博士学位,现为江南大学物联网工程学院副教授,主要研究领域为模式识别,机器学习。 Particle Com paction and Scheduling Based Particle Swarm Optim izationƽ ZHOU Dan1,2, GE Hongwei1,2+, SU Shuzhi1, YUAN Yunhao1 Key words:particle swarm optim ization; local optim ization; compaction; scheduling; accuracy of convergence; speed of convergence Abstract:To the problems of slow convergence and easy to fall into local optim ization appeared in standard particle swarm optimization, this paper proposes a particle compaction and scheduling based particle swarm optimization (PCS-PSO). Firstly, this paper presents the regulations of particles’compaction and scheduling. In order to avoid particles to stay in local optim ization, PCS-PSO evaluates dynam ically particle’s compaction and schedules the particle when the value of the particle’s compaction is beyond the threshold. Compared w ith standard particle swarm optim ization and other optimization algorithms using 11 benchmark functions, the experimental results show that PCS-PSO has better behaviors in convergence accuracy and speed. doi:10.3778/j.issn.1673-9418.1507025 E-mail: fcst@vip.163.com 文献标志码:A 中图分类号:TP185 仿真实验







6 结束语




1. School of Internet of Things Engineering, Jiangnan University, Wuxi, Jiangsu 214122, China
2. Key Laboratory of Advanced Process Control for Light Industry, M inistry of Education, Jiangnan University, Wuxi, Jiangsu 214122, China
+ Corresponding author: E-mail: ghw8601@163.com

