基于改进置信规则库推理的分类方法*
叶青青,杨隆浩,傅仰耿+,陈晓聪
基于改进置信规则库推理的分类方法*
叶青青1,杨隆浩2,傅仰耿1+,陈晓聪1
1.福州大学数学与计算机科学学院,福州350116 2.福州大学经济与管理学院,福州350116
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(05)-0709-13
http://www.ceaj.org Tel: +86-10-89056056
* The National Natural Science Foundation of China under Grant Nos. 61300026, 71371053, 71501047 (国家自然科学基金); the Natural Sci-ence Foundation of Fujian Province under Grant No. 2015J01248 (福建省自然科学基金); the National Collegiate Innovation and Entrepreneurship Training Program of China under Grant No. 201410386009 (国家级大学生创新创业训练计划项目); the Social Science Research Supported Foundation of Fuzhou University under Grant No. 14SKF16 (福州大学社科科研扶持基金).
Received 2015-06,Accepted 2015-08.
CNKI网络优先出版: 2015-08-12, http://www.cnki.net/kcms/detail/11.5602.TP.20150812.1630.004.htm l
摘要:通过引入置信规则库的线性组合方式,设定规则数等于分类数及改进个体匹配度的计算方法,提出了基于置信规则库推理的分类方法。比较传统的置信规则库推理方法,新方法中规则数的设置不依赖于问题的前件属性数量或候选值数量,仅与问题的分类数有关,保证了方法对于复杂问题的适用性。实验中,通过差分进化算法对置信规则库的规则权重、前件属性权重、属性候选值和评价等级的置信度进行参数学习,得到最优的参数组合。对3个常用的公共分类数据集进行测试,均获得理想的分类准确率,表明新分类方法合理有效。
关键词:置信规则库;基于证据推理的置信规则库推理方法(RIMER);参数学习;分类方法
1 引言
随着信息时代的到来,互联网、医学、金融等领域源源不断地产生大量的数据,数据的丰富带来了对强有力的数据分析工具的需求,其中数据分类技术就是典型的一种,因为很多工程实际问题都可以转化为分类问题。目前,数据分类技术主要建立在传统的数据挖掘算法上,包括决策树算法、贝叶斯(Bayes)算法、神经网络算法、粗糙集算法、支持向量机以及模糊系统等。上述方法由于涉及的参数较多,且较难以通过解释性的定义描述各类参数的含义,因此被称为“黑箱”式的方法。
基于证据推理的置信规则库推理方法(belief rulebase inference methodology using evidence reasoning,RIMER)由Yang等人[1]首次提出,其涵盖了Dempster-Shafer证据理论[2-3]、决策理论[4]、模糊理论[5]和传统IFTHEN规则库[6]等基础知识。目前,RIMER方法得到广泛应用,主要包括输油管道检漏[7]、石墨成分检测[8]和军事能力评估[9]等工程领域。相比上述“黑箱”式的方法,RIMER方法则是一个“白箱”模型,其整个推理过程和涉及的参数学习过程是可见、可控的。同时,RIMER方法中的置信规则库(belief rule base, BRB)具有置信结构,增加了RIMER方法的可理解性。
对于RIMER方法的具体应用,其一般不适用于前件属性数量过多的决策问题,否则将由于前件属性及候选值的数量过多而导致规则数的“组合爆炸”问题。该问题产生的根源在于BRB的构建需要覆盖所有的前件属性和各个候选值,因此当实际问题过于复杂时,BRB中的置信规则数势必呈指数级增长趋势。鉴此,本文基于RIMER方法提出了改进置信规则库推理的分类方法。新方法改进了传统构建BRB的方式,对前件属性候选值进行线性组合生成规则,由于设定规则数等于分类数,使得新分类方法能够很好地适应不同规模的决策问题,不再受限于前件属性或候选值的数量。在推理过程中,充分考虑距离与个体匹配度之间负相关关系,以输入值到候选值之间的距离倒数的归一化值作为个体匹配度,并用于计算规则的激活权重。在这种改进方式下,对于一组给定的测试数据,将激活所有的规则,这意味着本文方法考虑了BRB中每一条规则对于分类结果的贡献度,同时以距离作为衡量该贡献度大小的标准。新分类方法不仅延续了RIMER方法能够有效利用不完整或不精确信息对复杂问题进行建模的能力,而且有效地解决了RIMER方法不适用于多属性数据的分类问题。为验证本文方法的有效性,在实验部分对University of California at Irvine(UCI)分校的网站上3个常用的公共测试数据集进行了实验,通过对比前人方法可知,本文方法具有更理想的分类准确性。
2 RIMER方法
RIMER方法是一种能够利用不完整或不精确信息对复杂问题进行建模的方法,包括已知信息的规则化表示和决策过程的规则推导两个部分。目前,该方法在解决回归问题和分类问题时已卓有成效。
2.1已知信息的规则化表示
人工智能领域,以规则的形式表示已知信息是一种常见的方式,而在RIMER方法中,信息的规则化表示则体现在BRB中,其中BRB的四元组形式表示如下:

其中,U={Ui;i=1,2,…,T}是规则的前件属性集合,T表示BRB中前件属性的总数;A={Ai={Ai,j};i=1, 2,…,T;j=1,2,…,Ji}表示前件属性的候选值集合,Ai表示第i个前件属性的候选值集合,Ai,j表示第i个前件属性的第j个候选值,Ji表示第i个前件属性的候选值总数;D={Dn;n=1,2,…,N}表示后件属性的评价等级集合,Dn表示第n个评价等级,N表示评价等级的总数;F表示前件属性与后件属性之间的函数关系。依据BRB的四元组,当前件属性间以逻辑关系“与”相连时,则BRB中第k条规则表示如下:
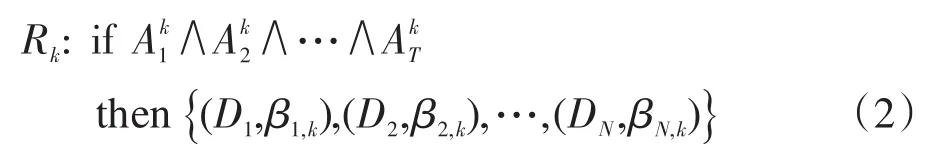
其中,Rk(k=1,2,…,L)表示第k条规则,L表示BRB中规则的总数;Aki表示第k条规则中第i个前件属性的候选值,因此有Aki∈Ai;βn,k表示第k条规则中后件属性的第n个评价等级上的置信度,若βn,k<1,称第k条规则包含完整的信息,否则称第k条规则包含不完整的信息。此外,称θk为第k条规则的规则权重,表示规则间的重要程度;称δi(i=1,2,…,T)为第i个前件属性的属性权重,表示属性间的重要程度。
2.2回归问题中的规则推导
回归问题是RIMER方法最早解决的问题,诸如输油管道检漏[10]、装备故障检测[11]和消费者偏好预测[12]等问题。在问题求解过程中,RIMER方法共包含两个步骤,分别为激活权重的计算和激活规则的合成。为提升RIMER方法的决策准确性,BRB的参数学习已成为RIMER方法中不可或缺的一部分。
2.2.1激活权重的计算
激活权重的计算是指利用给定的输入值及BRB中的权重参数计算各条规则的权重,并以此为度量标准决定BRB中用于合成输出值的规则。在激活权重计算中,首先需要计算前件属性各个候选值上的个体匹配度,给定输入值向量为:
x={x1,x2,…,xT}(3)
以第i个前件属性为例,由其输入值xi及候选值集合Ai={Aki;k=1,2,…,L},并根据基于效用的信息转化技术[13]可算得个体匹配度为:

当以分布式框架表示第i个前件属性的个体匹配度时,可表示如下:
S(xi)={(Ai,j,αi,j); i=1,2,…,T; j=1,2,…,Ji}(5)
其中,αi,j是第i个前件属性中第j个候选值Aji的个体匹配度。依据式(5)可同样算得其他前件属性各个候选值上的个体匹配度。然后根据BRB中每条规则所包含候选值的个体匹配度及权重参数计算规则的激活权重,其中第k条规则的激活权重计算公式为:

2.2.2激活规则的合成
由2.2.1节中计算的激活权重可知,当激活权重大于0时,当前规则处于激活状态需用于合成最终的决策结果,而激活规则的合成步骤如下所示。
首先,由激活规则后件属性的置信度和激活权重计算基本可信值[14-15]:

式中n=1,2,…,N,i=1,2,…,L。
然后,利用证据推理(evidential reasoning,ER)算法的解析公式[16]将所有的激活规则一次合成,合成公式为:

接着,计算合成结果中各个评价等级上的置信度:

最后,依据后件属性中各个评价等级的等级效用值μ={μ(D1),μ(D2),…,μ(DN)}计算给定输入值的期望型输出:

2.2.3 BRB的参数学习
RIMER方法的决策准确性与BRB中参数取值相关,在简单决策问题中,可由专家根据历史信息和先验知识给定。但该方式具有主观局限性,无法保证在复杂决策问题中RIMER方法的决策准确性,因此BRB的参数学习为研究者所关注。
BRB的参数学习是指利用历史数据分析RIMER方法与实际系统的输出误差,通过误差反复地调整BRB内部的参数取值,进而提高RIMER方法的决策准确性,如图1所示。由此可见BRB的参数学习实质上是一个带约束条件的优化问题,详见文献[17]。
目前,可用于BRB参数学习的方法主要包括FM INCON函数[17]和群智能算法[18]等。FM INCON函数是Matlab优化工具箱中用于求解非线性优化问题的函数,依此对BRB参数学习进行研究的成果有:Yang等人[17]提出的局部参数学习方法和Chen等人[19]提出的全局参数学习方法等,但上述方法均存在收敛速度慢,收敛精度不高的问题。相比于FM INCON函数,利用群智能算法对BRB进行参数学习具备对参数初值不敏感,收敛速度快和收敛精度高的优点,已有的研究成果有:Chang等人[20]提出的基于差分进化算法的参数学习方法和Zhou等人[21]提出的基于克隆选择算法的参数学习方法和苏群等人[22]提出的基于粒子群算法的参数学习方法。
2.3分类问题中的规则推导
分类问题是回归问题的特殊情形,前者属于离散型输出,而后者属于连续性输出,因此相比于回归问题中的规则推导,在分类问题的最终输出中还需进行分类映射。目前,RIMER方法在分类问题[21]中的应用主要包括:淋巴结疾病诊断和UCI分类数据集测试[23]。
2.3.1 BRB分类方法与分类映射
目前,RIMER方法在求解分类问题时共分成了两种BRB分类方法:
第一种BRB分类方法改进于回归问题中的RIMER方法。首先,在构建BRB时并非使用传统的遍历每个前件属性所有候选值的方式,而是通过线性组合的方式构建BRB中各条规则,如图2所示。

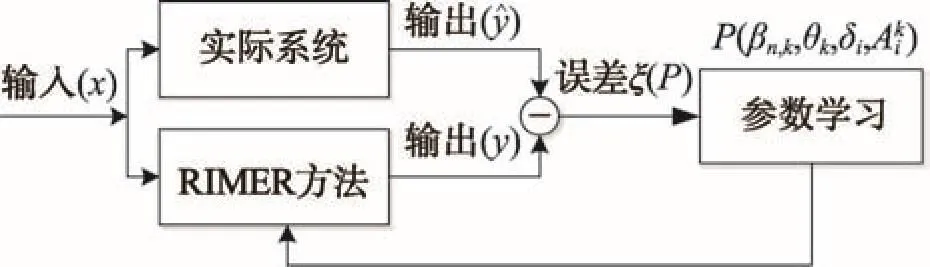
Fig.1 Parameter training model of BRB图1 BRB的参数训练模型

Fig.2 Different ways of combining rules图2 规则的不同组合方式
最后,利用激活规则合成中式(7)~(16)可推得各个评价等级上的置信度,并由分类映射确定最终分类结果。假设后件属性中评价等级与分类等级一一对应,则相应的最终分类结果为:

第二种BRB分类方法扩展于回归问题中的RIMER方法。BRB的构建采用遍历组合的方式,而算法流程包括BRB的参数学习,激活权重计算,激活规则合成和分类映射4个部分,鉴于与2.2节中介绍内容相同,此处不再赘述。
2.3.2现有BRB分类方法的不足
现有BRB分类方法在一定程度上已能有效地解决分类问题,但其在具体应用时仍存在一些不足之处。
对于第二种BRB分类方法,在构建BRB时采用遍历组合的方法,因此其继承了传统RIMER方法中固有的“组合爆炸”问题。以分类问题中常用的数据集Cancer为例,数据集Cancer中共有前件属性30个,假设每个前件属性的候选值个数为2,则由此构建的BRB中共有规则数230=1 073 741 824条,若再增加BRB中前件属性数量或候选值数量,则BRB中的规则数呈指数递增的趋势;同时,通过对UCI上231组分类数据集分析可知,前件属性数量少于10的分类数据集个数为54组,前件属性数量为10至100的分类数据集个数为114组,前件属性数量大于100的分类数据集个数为42组,由此可见现有的分类问题中多为多属性的情形,因此第二种BRB分类方法并不适用于处理现有分类问题。
对于第一种BRB分类方法[24],其中BRB的构建是以线性组合的方式,有效地避免了规则数的“组合爆炸”问题,但在构建BRB时未有合理的确定规则数的方式,进而易出现因BRB中规则数过少降低RIMER方法的分类准确性或因BRB中规则数过多增加参数学习的时空复杂度的问题。为避免BRB中规则的“零激活”问题,第一种BRB分类方法将各条规则上候选值对应的个体匹配度以累加求和的方式计算激活权重,其物理意义用规则表示是各个候选值间以“或”的逻辑关系相互关联,有悖于式(2)中规则的候选值间以“和”的逻辑关系进行关联的表示形式。
此外,在两种BRB分类方法中均只度量与输入值相邻候选值上的个体匹配度,而在基于效用的信息转化技术中距离是度量个体匹配度的依据,因此未考虑非相邻候选值的个体匹配度度量方式的合理性有待进一步分析。
3 改进置信规则库推理的分类方法
针对现有BRB分类方法存在的不足,及避免RIMER方法可能出现的规则数“组合爆炸”问题和规则“零激活”问题,本文提出了一种基于改进置信规则库推理的分类方法。以下将在3.1节中具体介绍新方法的算法步骤,并在3.2节中分析其在推理方面的合理性。
3.1算法步骤
改进置信规则库推理的分类方法的流程如图3所示。

Fig.3 Process of classification for BRB图3 置信规则库分类方法的流程
由图3可知,新分类方法的具体步骤为:
步骤1依据分类问题中分类数据集构建初始BRB。
假设分类问题中属性数量为T,训练数据的组数为H,已知分类数为C,分类数据集的矩阵形式为:

其中,Pi表示矩阵的第i行,即第i组输入数据构成的行向量;Uj表示矩阵的第j列,即所有输入数据的第j个属性构成的列向量;xi,j为矩阵的一个元素,表示第i组分类数据的第j个属性取值。
由此可确定BRB中有T个前件属性,每个前件属性设置C个候选值,效用等级个数设置为C,依据线性组合方式可知,BRB中规则数为C。
步骤2依据分类数据集设置初始BRB的参数取值。
针对BRB中各类的参数,由分类数据集可确定其参数取值。
(1)对于BRB中第k条规则,其规则权重初值可设置为:
θk=1
(2)对于第i个前件属性,其属性权重初值可设置为:
δi=1
(3)对于第k条规则中的第i个前件属性,其各个候选值的初值可设置为:

(4)每一个评价等级都对应一个分类,评价等级Dn设置为:

(5)第k条规则中第n个评价等级对应的置信度设置为:

其中,randi( )表示0到1之间的长度为C的随机数序列中的第i个取值。
步骤3对初始BRB的参数进行训练,得到最优参数取值。
初始BRB中待优化的参数包括前件属性权重δi、属性候选值Aki、规则权重θk和评价等级的置信度βn,k。本文使用全局参数优化模型,可以表示如下:
P=P(θk,δi,βn,k, Aki)(23)
对于优化模型中的等式和不等式约束条件,给出如下定义。
(1)标准化规则权重θi,其不小于0且不大于1,即:
0≤θk≤1, k=1,2,…,L(24)
其中,L表示BRB中的规则数。
(2)标准化前件属性权重δi,其同样不小于0且不大于1,即:
0≤δi≤1, i=1,2,…,T(25)
其中,T表示BRB中前件属性的数量。
(3)任意一条置信规则的结果置信度均不小于0且不大于1,其中第k条规则的第j个评价等级上的置信度需满足:
0≤βn,k≤1, n=1,2,…,N, k=1,2,…,L(26)
其中,N表示BRB中效用等级的个数。
(4)假设第k条规则是完整的,即输入不包含不确定、模糊信息,则该条规则的结果置信度之和等于1:

(5)标准化属性候选值,使其不大于训练数据属性取值的上限,不小于其下限,且同一属性需满足相邻规则的候选值相差一个无穷小量Vi,即:
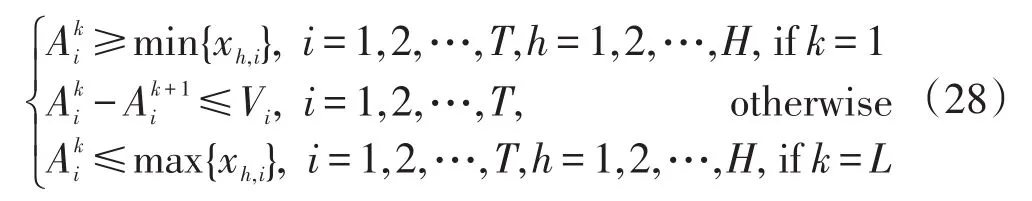
其中, H表示训练数据的组数。
步骤4给定分类问题的前件属性,通过RIMER方法及分类映射得到分类结果。
当制定规则的形式为前件属性的线性组合时,由于规则的删减,使得规则的组合并不能覆盖所有的属性候选值,无法保证对于一组给定的数据能够激活某些规则,传统的推理方式将无法进行。
鉴此,本文对传统BRB中计算个体匹配度的函数进行改进,将输入值到指定规则中对应属性的候选值的距离倒数的归一化值作为个体匹配度,则其个体匹配度的计算如下所示:

其中,xi表示式(3)中测试数据x的第i个属性输入值;Aki表示第i个属性在第k条规则中的候选值;L为规则数;αi,k表示输入数据对于第k条规则中的第i个属性的个体匹配度。
在得到个体匹配度后,接着可以按照式(6)计算规则的激活权重,按照式(7)~(16)合成激活规则,最后由式(19)得到最终的分类结果。
3.2合理性分析
3.2.1个体匹配度计算的合理性
传统的RIMER方法中,计算规则的激活权重时,其个体匹配度的计算公式如式(4)所示。以下对其过程进行简要描述:首先对于一组输入数据中的第i个前件属性xi,找到其在BRB中对应属性的候选值区间,如图4所示,xi处在规则b和规则c对应的区间中,即候选值区间为[Abi, Aic],其个体匹配度为:

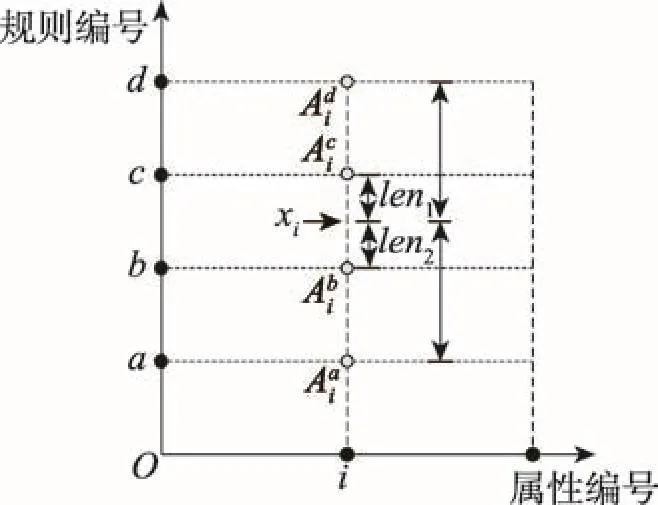
Fig.4 Different ways of calculating indivial matching图4 计算个体匹配度的不同方式
由于xi处于规则b和规则c的第i个属性候选值之间,xi对于其他规则的个体匹配度均为0。得到个体匹配度后,便可用于计算规则的激活权重。
将上述计算过程运用于解决多属性的分类问题时,因受限于规则的数量,以上方法并不适用,导致无法保证一定有规则被激活,由此可见现有方法存在一定局限性。此外,由图4可知,当以线性组合的方式构建规则时,输入值xi到每条规则的第i个属性的候选值的距离并不相同,例如xi到候选值Adi和Aai的距离并不相等,因此规则a和规则d在使用xi计算规则匹配度时其影响程度并不相同,但传统的RIMER方法认为输入值xi对规则a和规则d无影响。
鉴此,本文依据个体匹配度与输入值到规则中对应候选值的距离负相关关系,提出如式(29)所示的个体匹配度计算的改进方法。以下通过一个简单的曲线拟合实例验证该个体匹配度计算方法的合理性。
假设二元复合幂函数为:

其中分别令τ=-3, -1, 1, 3,自变量x的取值范围为[6,21],自变量y的取值范围为[4,10],由定义域内均匀选取的3 000组数据作为BRB参数学习的训练数据。基于个体匹配度计算改进方法的曲线拟合结果如图5。

Fig.5 Fitting of function图5 函数的拟合情况
由图5可知,上述4个二元函数的拟合效果理想,进而说明了本文提出的个体匹配度计算改进方法的合理性。
3.2.2规则数设置的合理性
对于BRB中规则数量的设定,假若规则数量太少,则分类准确性可能难以让人满意;假若规则数量太多,则可能导致运行效率低下且分类准确性不理想。因而这就要求针对特定的研究问题设置合理的规则数量。为此,本文提出通过分类问题中分类数量来确定BRB中的规则数量,即规则数等于分类数。其合理性分析如下:
当规则数少于分类数时,如图6所示,个体匹配度计算公式改进后,同类别分类数据的输入值易激活同一规则,且该条规则在激活规则合成时占主导作用。因此针对规则数少于分类数的情形,势必造成最终分类出现无规则相对应的问题,最终降低方法的分类准确性。

Fig.6 Mapping of rule and class图6 规则与分类的对应
当规则数多于分类数时,假设分类问题共有C个分类、T个前件属性、N个后件属性评价等级时,则BRB中需要参数学习的参数数量共为C+T+C× T+C×N。假定参数学习时划分到每个参数的平均时间复杂度为O(K),则参数学习的时间复杂度为:
O(K×(C+T+C×T+C×N))≈O(C×K×(T+N))(31)
由上述公式可见,每增加一条规则所需提高的时间复杂度为O(K×(T+N))。因此,从算法时间复杂度的角度分析,BRB中不宜设定过多的规则。
当规则数等于分类数时,如图6所示,由于每一条规则根据其参数特征与特定分类建立一一对应关系,例如图6中共有n条规则和n个分类,对于第k个分类,n条规则对其都存在一定的决定因素,但就决定能力而言,第i条规则对其有最大的决定能力,如80%,其余规则对其决定能力相对较小,如8%、5%等。因此使用规则数等于分类数的规则制定策略,可提高方法的分类准确性,并且使分类方法具有最低的时间复杂度。
4 实例分析
4.1实验环境及实例背景
在使用本文方法进行数据分类时,以差分进化算法[25]作为BRB参数学习的优化算法,其中种群规模NP=200,进化代数genSize=1 000,缩放因子F=0.5,交叉概率CR=0.9。此外,实验环境为:Intel®Core i5-4570@3.20 GHz;4 GB内存;W indows 7操作系统;算法由Visual C++ 6.0编写。
对于实验中所用的测试数据集,本文选自UCI公共测试数据集中乳腺癌数据Breast Cancer[26]、鸢尾花特征数据Iris[27]和玻璃类型数据Glass[28]。表1列举了上述3个测试数据集中前件属性数量、分类类别数量和测试集大小等信息。

Tabel 1 Basic information of test data sets表1 测试数据集的基本信息
4.2实验过程
实验中,对于以上3个数据集,分别测试当规则数为分类数上下范围时的分类准确性。Breast Cancer 和Iris数据集分别测试当规则数为2到5条时的分类准确率,Glass数据集分别测试当规则数为5到9条时的分类准确率,同时统计其分类准确率的标准差。为说明本文方法的具体应用,以Iris数据集为例,具体介绍本文的算法步骤。

Table 2 Initial belief rule base表2 初始置信规则库

Table 3 Trained belief rule base表3 参数训练后的置信规则库
首先,取规则数L=3构建初始的置信规则库。根据3.1节步骤1和步骤2可构出如表2所示的Iris数据集的初始BRB。
然后通过差分进化算法,按照3.1节步骤3所述,训练BRB中各个参数,得到如表3所示的参数训练后的BRB。
在得到表3的BRB表示后,对于给定的输入数据,可按照3.1节中步骤4推理相应的分类结果。
对于实验结果有效性验证,本文采用十折交叉验证法,即每次取90%的数据作为训练数据,剩下10%的数据作为测试数据。而在算法的效率分析中,同样以Iris数据集为例,针对不同的规则数,算法所需时间如表4所示。

Table 4 Time for training parameters表4 BRB参数训练时间
由表4中数据可绘制如图7所示的折线图。
根据图7可知,对于以上的Iris数据集,随着规则数的增加,其训练时间也随之增加,并且大致呈线性关系,与3.2.2小节中所述合理性相符。综上所述,构建BRB时的规则数不应设置过多。
4.3结果分析

Fig.7 Time of training parameters图7 参数训练时间
为进一步验证本文方法的有效性,用表1所示的3个数据集进行测试,其中图8、图9和图10分别为3个数据集在设定不同规则数时,10次十折交叉验证的分类准确率。对应给定的规则数,都有10个点表示相应的准确率,由于某些点的重叠,图上对应规则数的可见点可能小于10个。
同时,表5统计了3个数据集在给定规则数时10次验证结果的标准差信息以及算法中训练优化模型所用的时间。在训练和验证每个数据集时,规则数N均取在以其分类数为中心的指定区间内,由于当N小于2时,RIMER方法无法进行规则推导,规定N的下限为2。在表5中,加粗的数据表示当前数据集的分类数等于规则数的情况。
为了使以上的数据更加直观,绘制如图11、图12和图13所示的折线图。图11为Breast Cancer数据集的分类准确率及其标准差变化的折线图;图12为Iris数据集的分类准确率及其标准差变化的折线图;图13为Glass数据集的分类准确率及其标准差变化的折线图。

Fig.8 Classification accuracy of Breast Cacncer图8 Breast Cancer数据集分类准确性统计

Fig.9 Classification accuracy of Iris图9 Iris数据集分类准确性统计
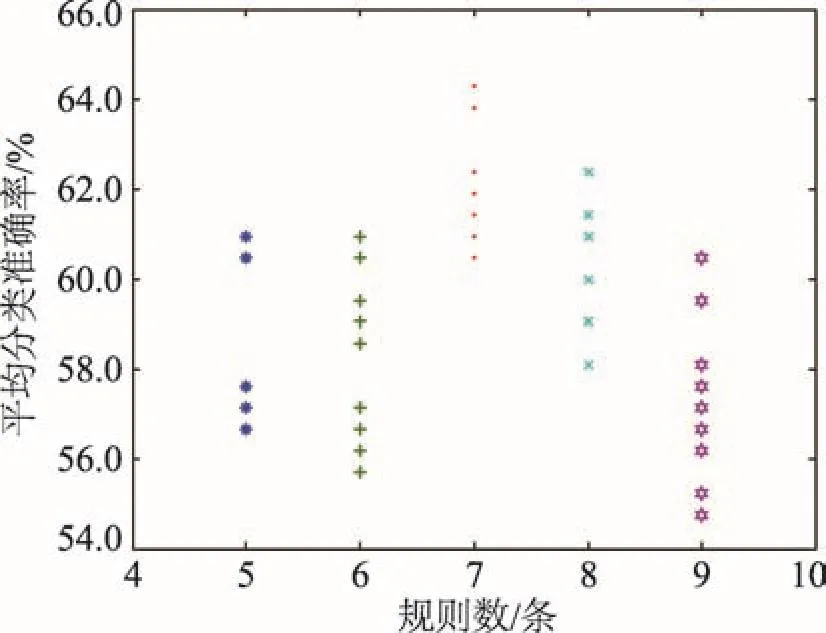
Fig.10 Classification accuracy of Glass图10 Glass数据集分类准确性统计

Table 5 Classification accuracy of 3 datasets表5 3个数据集的分类准确率

Fig.11 Classification accuracy and standard deviation of Breast Cancer图11 Breast Cancer分类准确率及其标准差

Fig.12 Classification accuracy and standarddeviation of Iris图12 Iris分类准确率及其标准差

Fig.13 Classification accuracy and standard deviation of Glass图13 Glass分类准确率及其标准差
根据图11、图12和图13可知,分类准确率的变化趋势与其标准差的变化趋势基本上呈现负相关的关系。例如Breast Cancer数据集在规则数为2条时,分类准确率最高,标准差最小;Iris数据集在规则数为3条时,分类准确率最高,标准差最小;Glass数据集在规则数为7条时,分类准确率最高,标准差最小。因此由以上3个数据集的测试结果表明,当BRB中的规则数刚好等于分类数时,其分类准确率最高,标准差最小。
为了验证本文方法的有效性,表6列出了与Fallahnezhad等人[29]总结的部分前人成果的对比。

Table 6 Comparison of classification accuracy w ithdifferent methods表6 不同方法的平均分类准确率对比
根据表6可知,对于3个测试数据集,用本文分类方法的分类准确性均较理想,其中在Breast Cancer 和Iris数据集中都取得了仅次于最优准确性的结果。
5 结束语
目前,面对海量数据处理时,分类问题是研究的热点。本文提出了基于改进置信规则库推理的分类方法,首先将分类问题的分类数与置信规则库的规则数相关联,设置规则数等于分类数,同时改进了传统置信规则库中个体匹配度的计算方法,然后将置信等级映射为分类结果。相比现有基于置信规则库的分类方法,本文方法有效地克服了规则数的“组合爆炸”问题和规则的“零激活”问题。在实例分析部分,通过对3个公共测试数据集的多次实验,验证了当规则数等于分类数时,其分类准确性较高的结论,同时其分类准确性较当前文献的研究方法具有较大的优势。
References:
[1] Yang Jianbo, Liu Jun, Wang Jin, et al. Belief rule-base inference methodology using the evidential reasoning approach-RIMER[J]. IEEE Transactions on Systems, Man and Cybernetics: Part A Systems and Humans, 2006, 36(2): 266-285.
[2] Dempster A P. A generalization of Bayesian inference[J]. Journal of the Royal Statistical Society: Series B Methodological, 1968, 30(2): 205-247.
[3] Shafer G. A mathematical theory of evidence[M]. Princeton, USA: Princeton University Press, 1976.
[4] Hwang C L, Yoon K. Methods for multiple attribute decision making[M]//Multiple Attribute Decision Making. Berlin, Heidelberg: Springer, 1981: 58-191.
[5] Zadeh L A. Fuzzy sets[J]. Information and Control, 1965, 8 (3): 338-353.
[6] Sun R. Robust reasoning: integrating rule-based and similaritybased reasoning[J]. Artificial Intelligence, 1995, 75(2): 241-295.
[7] Zhou Zhijie, Yang Jianbo, Hu Changhua. Confidence expert system rule base and complex system modeling[M]. Beijing: Science Press, 2011.
[8] Yang Jianbo, Liu Jun, Xu Dongling, et al. Optimization models for training belief-rule-based systems[J]. IEEE Transactions on Systems, Man and Cybernetics: Part A Systemsand Humans, 2007, 37(4): 569-585.
[9] Jiang Jiang, Li Xuan, Zhou Zhijie, et al. Weapon system capability assessment under uncertainty based on the evidential reasoning approach[J]. Expert Systems w ith Applications, 2011, 38(11): 13773-13784.
[10] Zhou Zhijie, Hu Changhua, Yang Jianbo, et al. Online updating belief rule based system for pipeline leak detection under expert intervention[J]. Expert System w ith Application, 2009, 36(4): 7700-7709.
[11] Zhou Zhijie, Hu Changhua, Xu Dongling, et al. A model for real-time failure prognosis based on hidden Markov model and belief rule base[J]. European Journal of Operational Research, 2010, 207(1): 269-283.
[12] Wang Yingm ing, Yang Jianbo, Xu Dongling, et al. Consumer preference prediction by using a hybrid evidential reasoning and belief rule-based methodology[J]. Expert System w ith Application, 2009, 36(4): 8421-8430.
[13] Yang Jianbo. Rule and utility based evidential reasoning approach for multi-attribute decision analysis under uncertainties[J]. European Journal of Operational Research, 2001, 131(1): 31-61.
[14] Wang Yingm ing, Yang Jianbo, Xu Dongling. Environmental impact assessment using the evidential reasoning approach[J]. European Journal of Operational Research, 2006, 174(3): 1885-1913.
[15] Duan Xinsheng. Evidence theory, decision & artificial intelligence[M]. Beijing: Renmin University of China Press, 1993. [16] Wang Yingm ing, Yang Jianbo, Xu Dongling, et al. The evidential reasoning approach for multiple attribute decision analysis using interval belief degrees[J]. European Journal of Operational Research, 2006, 175(1): 35-66.
[17] Yang Jianbo, Liu Jun, Xu Dongling, et al. Optim ization models for training belief-rule-based systems[J]. IEEE Transactions on Systems, Man and Cybernetics: Part A Systems and Humans, 2007, 37(4): 569-585.
[18] Wang Zhengzhi, Bo Tao. Evolutionary computation[M]. Changsha: National University of Defence Technology Press, 2000.
[19] Chen Yuwang, Yang Jianbo, Xu Dongling, et al. Inference analysis and adaptive training for belief rule based systems[J]. Expert System Application, 2011, 38(10): 12845-12860.
[20] Chang Leilei, Sun Jianbin, Jiang Jiang, et al. Parameter learning for the belief rule base system in the residual life probability prediction of metalized film capacitor[J]. Know ledge-Based System, 2015, 73: 69-80.
[21] Zhou Zhiguo, Liu Fang, Jiao Licheng, et al. A bi-level belief rule based decision support system for diagnosis of lymph node metastasis in gastric cancer[J]. Know ledge-Based System, 2013, 54: 128-136.
[22] Su Qun, Yang Longhao, Fu Yanggeng, et al. Parameter training approach based on variable particle swarm optimization for belief rule base[J]. Journal of Computer Applications, 2014, 34(8): 2161-2165.
[23] Jiao Lianmeng, Pan Quan, Denoeux T, et al. Belief rulebased classification system: extension of FRBCS in belief functions framework[J]. Information Sciences, 2015, 309: 26-49.
[24] Chang Leilei, Zhou Zhijie, You Yuan, et al. Belief rule based expert system for classification problems w ith new rule activation and weight calculation procedures[J]. Information Sciences, 2016, 336: 75-91.
[25] Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optim ization over continuous spaces [J]. Journal of Global Optim ization, 1997, 11(4): 341-359.
[26] Aci M, Avc M. K nearest neighbor reinforced expectation maxim ization method[J]. Expert Systems w ith Applications, 2011, 38(10): 12585-12591.
[27] Fisher R A. The use of multiple measurements in taxonom ic problems[J].Annual Eugenics, 1936, 7(2): 179-188.
[28] Athitsos V, Sclaroff S. Boosting nearest neighbor classifiers for multiclass recognition, 2004-006[R]. Boston University, 2004.
[29] Fallahnezhad M, Moradi M H, Zaferanlouei S. A hybrid higher order neural classifier for handling classification problems[J]. Expert Systems w ith Applications, 2011, 38 (1): 386-393.
附中文参考文献:
[7]周志杰,杨剑波,胡昌华.置信规则库专家系统与复杂系统建模[M].北京:科学出版社, 2011.
[15]段新生.证据理论与决策、人工智能[M].北京:中国人民大学出版社, 1993.
[18]王正志,薄涛.进化计算[M].长沙:囯防科技大学出版社, 2000.
[22]苏群,杨隆浩,傅仰耿,等.基于变速粒子群优化的置信规则库参数训练方法[J].计算机应用, 2014, 34(8): 2161-2165.

YE Qingqing was born in 1992. She is a student at College of Mathematics and Computer Science, Fuzhou University. Her research interests include intelligent decision making technology and data mining, etc.
叶青青(1992—),女,福建宁德人,福州大学数学与计算机科学学院学生,主要研究领域为智能决策技术,数据挖掘等。

YANG Longhao was born in 1990. He is a Ph.D. candidate at School of Econom ics and Management, Fuzhou University. His research interests include intelligent decision making technology and belief rule base inference, etc.
杨隆浩(1990—),男,福建南平人,福州大学经济与管理学院博士研究生,主要研究领域为智能决策技术,置信规则库推理等。

FU Yanggeng was born in 1981. He received the Ph.D. degree from Fuzhou University in 2013. Now he is a lecturer at College of Mathematics and Computer Science, Fuzhou University, and the member of CCF. His research interests include multi-criteria decision making under uncertainty, belief rule base inference and mobile Internet applications, etc.
傅仰耿(1981—),男,福建泉州人,2013年于福州大学获得博士学位,现为福州大学数学与计算机科学学院讲师,CCF会员,主要研究领域为不确定多准则决策,置信规则库推理,移动互联网应用等。

CHEN Xiaocong was born in 1994. He is a student at College of Mathematics and Computer Science, Fuzhou University. His research interests include intelligent decision making technology and data mining, etc.
陈晓聪(1994—),男,福建龙岩人,福州大学数学与计算机科学学院学生,主要研究领域为智能决策技术,数据挖掘等。
Classification Approach Based on Im proved Belief Rule-Base Reasoningƽ
YE Qingqing1, YANG Longhao2, FU Yanggeng1+, CHEN Xiaocong1
1. College of Mathematics and Computer Science, Fuzhou University, Fuzhou 350116, China 2. School of Econom ics and Management, Fuzhou University, Fuzhou 350116, China
+ Corresponding author: E-mail: ygfu@qq.com
YE Qingqing, YANG Longhao, FU Yanggeng, et al. Classification approach based on im proved belief rulebase reasoning. Journal of Frontiersof Computer Science and Technology, 2016, 10(5):709-721.
Abstract:This paper proposes a new classification approach based on improved belief rule-base reasoning by introducing linear combinational mode, setting the number of rules based on the classifications and improving the method of calculating individual matching degree. Compared w ith the traditional belief rule-base inference methodology, the number of rules in the proposed method does not depend on the number of antecedent attributes or its referential values, and it is only related to classification number. In this way, the new method can ensure the applicability for complex problems. In the experiments, the differential evolution algorithm is applied to train parameters, including rule weights, attribute weights, referential values of antecedent attributes and belief degrees. Three commonly public datasets have been employed to validate the proposed method. And the classification results are proved to be ideal, which shows that the proposed method is reasonable and effective.Key words: belief rule-base; belief rule-base inference methodology using evidence reasoning (RIMER); parameter learning; classification method
doi:10.3778/j.issn.1673-9418.1507068 E-mail: fcst@vip.163.com
文献标志码:A
中图分类号:TP18

