带混沌侦查机制的蚁狮优化算法优化SVM参数*

赵世杰，高雷阜，于冬梅，徒　君



带混沌侦查机制的蚁狮优化算法优化SVM参数*

赵世杰+，高雷阜，于冬梅，徒君

辽宁工程技术大学优化与决策研究所，辽宁阜新123000

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology 1673-9418/2016/10(05)-0722-10

http://www.ceaj.org Tel: +86-10-89056056

* The Specialized Research Fund for the Doctoral Program of Higher Education of China under Grant No. 20132121110009 (高等学校博士学科点专项科研基金); the Project of Liaoning Provincial Department of Education under Grant No. No.L2015208 (辽宁省教育厅基金项目).

Received 2015-06,Accepted 2015-09.

CNKI网络优先出版: 2015-09-06, http://www.cnki.net/kcms/detail/11.5602.TP.20150906.1638.010.htm l

ZHAO Shijie, GAO Leifu,YU Dongmei, et al.Ant lion optim izer w ith chaotic investigation mechanism for optim izing SVM parameters. Journal of Frontiersof Computer Scienceand Technology, 2016, 10(5): 722-731.

摘要：蚁狮优化算法作为一种新的仿生智能算法，有许多有待完善和发展的方面。由于在算法迭代过程中蚁狮种群存在适应度相对较差的个体，若蚂蚁选定该蚁狮进行随机游走将会增加算法陷入局部极值的可能性，同时会影响算法的寻优性能。针对该问题，借鉴人工蜂群算法的侦查思想，在蚁狮原有信息的基础上引进混沌搜索机制，提出了一种带混沌侦查机制的蚁狮优化算法。该算法首先将排序蚁狮种群中适应度较差的个体定义为侦查蚁狮，并将其原始位置信息作为Fuch混沌映射的初始值，然后通过一定次数的混沌搜索迭代获得一个适应度值更优的位置再重新赋值给侦查蚁狮，以提高蚁狮种群的优良性和算法的寻优性能。最后将改进蚁狮优化算法用于支持向量机参数的优化中，以UCI标准数据库中的数据进行数值实验，结果表明改进算法具有较强的寻优性能和较好的算法稳定性。

关键词：蚁狮优化算法；混沌；侦查机制；支持向量机；参数优化

1 引言

蚁狮优化算法[1]（ant lion optim izer，ALO）是由澳大利亚学者Seyedali于2015年提出的一种新的仿生智能优化算法。该算法通过蚂蚁围绕蚁狮进行随机游走实现对搜索空间的探索，并向选定蚁狮和精英进行学习，以保证种群的多样性和算法的寻优性能；同时ALO算法具有调节参数少，易于实现等优点，已被成功应用于三杆桁架设计、船舶螺旋桨形状优化等工程应用领域。

支持向量机[2]（support vector machine，SVM）是由Vapnik等人以统计学习理论为基础提出的一种机器学习方法，在解决小样本、非线性和高维数据时有效克服了过学习、欠学习和“维数灾难”等问题而得到广泛应用[3-5]。在利用支持向量机解决实际应用中的分类、回归问题时，需要对影响SVM性能的核参数和罚参数等进行优化选择，以提高SVM的推广泛化性能。目前常用的支持向量机参数优化方法主要有经验选择法、网格搜索法[6]和群体智能优化算法。但经验选择法对人的先验知识要求较为严格；网络搜索法需要对有限离散参数进行一一比对，较为费时，同时随着参数的增加，时间复杂度增加严重。相对而言，群体智能优化算法通过种群中多个个体的并行寻优以提高参数的寻优效率，且具有对初值不敏感等特性，是一类较为理想的SVM参数优化方法。基于群体智能算法优化SVM参数的方法主要有遗传算法[7]、粒子群算法[8-9]、蚁群算法[10-12]和多智能算法的融合方法[13]等。

ALO算法作为一种新的仿生智能优化算法，有许多有待改进的方面和新的应用领域。考虑到在ALO算法迭代寻优过程中，蚁狮种群存在适应度相对较差的个体，如果蚂蚁选定该蚁狮进行学习势必会增加陷入局部极值的可能性。同时由于该蚁狮在局部极值的邻域进行搜索而导致这些蚁狮个体的资源浪费，从而在一定程度上影响了ALO算法的寻优性能和收敛效率。为此，本文受人工蜂群算法中侦查蜂的思想启发，将蚁狮种群中适应度值相对较差的个体定义为侦查蚁狮，同时在原有位置信息的基础上通过一定次数的混沌搜索以获得适应度值更优的位置，并将其重新赋值给侦查蚁狮，从而提出了带混沌侦查机制的蚁狮优化算法（ant lion optimizer w ith chaos investigation mechanism，CIALO），最后将其用于SVM参数优化中，通过对UCI标准数据库中数据集的实例化分析来验证CIALO算法优化SVM参数的有效性和可行性。

2 蚁狮优化算法及改进算法

2.1蚁狮优化算法

蚁狮优化算法[1]是受自然界中蚁狮猎捕蚂蚁的狩猎机制启发而提出的一种新的群体智能优化算法。自然界中蚁狮在沙中沿圆形轨迹移动，利用下颚挖出一个诱捕蚂蚁的圆锥形坑，当随机移动的蚂蚁陷入坑中时，蚁狮便捕食之并重新修缮坑穴等待下一只猎物（蚂蚁）。

ALO算法就是模仿蚁狮和蚂蚁的这种相互作用来实现对问题的优化：蚂蚁通过围绕蚁狮的随机游走实现对搜索空间的探索，并向蚁狮和精英进行学习以保证种群的多样性和算法的寻优性能；蚁狮相当于问题的解，通过猎捕适应度高的蚂蚁实现对近似最优解的更新和保存。

ALO算法迭代寻优的执行伪码[1]为：

A lgorithm: Basic ALO algorithm

Initialize the first population of ants and antlions random ly Calculate the fitness of ants and antlions

Find the best antlions and assume it as the elite (determined optimum)

W hile the end criterion is not satisfied

For every ant

Select an antlion using Rouletee wheel Update c and d

Create a random walk and normalize it Update the position of ant EndFor

Calculate the fitness of all ants

Replace an antlion w ith its corresponding ant if becomes fitter

Update elite if an antlion becomes fitter than the elite

EndW hile Return elite

ALO算法具有相对较好的寻优效率和收敛精度：通过蚁狮的随机选择、蚂蚁的随机游走以及陷阱的自适应缩减边界等机制保证了算法对搜索空间的较好探索性能，实现了ALO算法的较快寻优效率。同时作为一种基于群体的智能算法，ALO算法通过随机游走和轮盘赌选择等策略降低了算法陷入局部极值的可能性，在一定程度上提高了算法的收敛精度。文献[1]将ALO算法与遗传算法、蝙蝠算法、萤火虫算法和花朵授粉算法等7种智能算法进行对比，通过对单峰函数、多峰函数和单多峰混合优化函数的大量实验，充分验证了ALO算法较好的寻优效率和收敛精度。

2.2带混沌侦查机制的蚁狮算法

ALO算法中通过蚂蚁围绕精英和轮盘赌选定蚁狮的随机游走实现对空间的搜索，但由于算法前期蚁狮种群中存在适应度值较差的个体（即离最优解较远的解），若蚂蚁轮盘赌选定该蚁狮进行随机游走则会陷入该局部最优解邻域，从而在一定程度上可能弱化种群的寻优性能且不利于算法整体收敛效率，同时也将造成这些蚁狮资源的浪费。鉴于此，需要将这些蚁狮进行重新赋值，以提高蚁狮种群的个体优良性和算法的整体寻优性能。

受人工蜂群算法（artificial bee colony,ABC）中侦查蜂的启发：侦查蜂实现对新蜜源的开采，有利于跳出局部极值并增强算法的寻优性能。将ABC算法中的这种侦查机制引入到ALO算法中，即在蚁狮种群中引入“侦查蚁狮”的概念，将适应度值较差的蚁狮定义为侦查蚁狮，通过对其位置的重新赋值实现对搜索空间的重新较优搜索；但侦查蚁狮位置的重新赋值并不是采用ABC算法中舍弃原有信息而只采用随机初始化的方式进行定义，而是在充分利用蚁狮原有位置信息的基础上，通过引进具有较好遍历性和互不相关性的混沌映射，利用一定次数的混沌迭代来获得适应度值相对较好的侦查蚁狮。

目前常用的混沌映射主要有Logistic映射、Tent映射等。但Logistic映射对初值设置敏感，只有在控制参数为4时才完全进入混沌状态，且遍历性和均匀性都相对较差（映射点边缘处密度很高而区间中央密度较低），这将直接影响混沌搜索的遍历性能；Tent映射虽遍历性较好，分布也较为均匀，但存在着小周期和有理数不动点，数据一旦落入不动点周期内势必会造成序列趋于稳定而使算法失效。鉴于上述分析，本文选用Fuch映射[14]作为定义侦查蚁狮的混沌映射，该映射具有对初值不依赖性、均衡遍历性和较高收敛效率等优点，具体定义式为：

其中，zi≠0，i∈Z+。图1展示了Fuch映射与Logistic 和Tent映射的初值依赖性对比情况。

由图1分析可知，Fuch映射具有较好的初值不依赖性：在初值z0=0.483 5微小变化10-6时，Fuch映射产生的混沌序列是完全不同且毫无规律的[14]，而Logistic和Tent映射则产生了较多的重叠点，且不重叠点处的绝大多数差距也几乎是相对较小的，甚至出现了Tent映射陷入不动点周期而使算法失效的情况（见图1（b）中60代后）。在Z+域内，Fuch映射均可直接代入混沌映射来产生有效的混沌序列，而Logistic 和Tent映射则需将初值限制在[0，1]区间内，一旦越界将会造成算法无效。为能生成有效的混沌序列必须先通过变换将其映入混沌定义域才可代入混沌映射，而生成的混沌值也必须通过逆变换将其映入优化变量定义域才能再代回到优化函数中继续进行迭代寻优。

Fig.1 Contrast on initial-value independency for three chaotic mappings图1 3种混沌映射的初值依赖性对比

CIALO算法可用于求解式（2）优化问题的最优解：

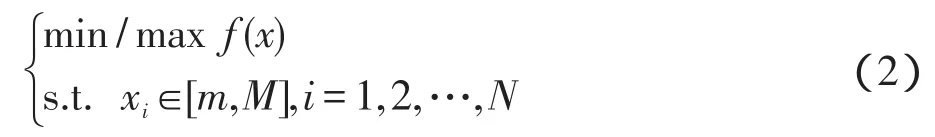
其中，N表示函数f(∙)中的变量数目。

假设混沌映射中混沌变量zi的定义区间为[l,u]，且一般与优化变量xi的约束区间[m,M]是不一致的，因此需要将混沌变量和优化变量进行转化变换。在将优化变量xi代入到混沌映射进行混沌搜索时，需要先将其转变为混沌变量zi，变换公式为：

利用混沌遍历搜索得到的侦查蚁狮新位置zi在进行适应度值计算时，需要将其转变为优化变量xi，变换公式为：

通过混沌变量与优化变量间的这种相互转换以实现侦查蚁狮的混沌搜索和适应度值计算间的相互跳转。由于Fuch映射具有对初值不依赖性，可以跳过式（3）直接执行式（4）来进行有效的混沌遍历。而Logistic映射、Tent映射等其他混沌映射则需要首先经过式（3）的变换才可以代入到混沌映射来进行混沌搜索，因此从算法执行操作的角度来说，采用Fuch映射在一定程度上有利于提高算法的计算效率。

利用CIALO算法优化最大值问题的执行伪码为：

A lgorithm: CIALO algorithm

Parameters: Numagent—The number of search agents

Itermax—The maximum iterations of algorithm dim—The variable dimension of continuous functions

m—The m inimum value ofvariable range

M—The maximum value ofvariable range

p0—The percentage of investigation antlions Numchaos—The number of chaotic search

Output: X*—The optimal solution (for maximum-value problem)

Set Numagent,Itermax,dim,m,M,p0,Numchaos

// Initialize the ants and antlions random ly MAnt=rand(Numagent,dim)*(ub-lb)+lb MAntlion=rand(Numagent,dim)*(ub-lb)+lb

// Calculate antlionsƳfitness, sort antlions descendingly and save elite

X*=E lite Iter=2 Repeat

for i=1,2,…,Numagent

// Create a random walk around selected antlion and elite // Update Ant

end for

// Calculate the fitness of all ants, sort ants and antlions descendingly according to the fitness and assign Top Numagentindividuals to antlions

// Calculate the number of substituted antlions(SAL)

NumSAL=Numagent*p0

For j=1,2,…,NumSAL

//Assign the j-th SALƳs position to chaotic variable x_chaos=Antlion(Agents*(1-p0)+j,:);

For k=1,2,…,Numchaos

// Chaotic search process

using Eq.(4)

// Calculate and compare the fitness, and update the j-th SAL

End If

EndFor

EndFor

// Sortnew antlionsdescendingly according to the fitness // Updata elite

if fitness(AntlionIter(1))>fitness(Elite)

Elite=AntlionIter(1) endif

Iter=Iter+1

Until Iter=Itermax+1

Return X*=Elite

3 CIALO优化SVM参数

CIALO算法可用于SVM参数的优化选择。SVM分类模型中需要优化的参数主要是罚参数C和核参数。罚参数C主要是对错分样本的惩罚，是在机器结构风险和泛化性能之间寻求一种折中；核参数主要影响核函数的分析性能，进而影响SVM的泛化性能。目前常见的核函数主要有多项式核、RBF核、Sigmoid核等，考虑到RBF核只有一个待优化参数，且对低维和高维空间数据均具有较好的适用性，本文选用RBF核作为SVM核函数，其表达式为：

令g=1/2r2，则SVM中待优化参数为罚参数C和核参数g。对分类问题，一般以SVM的分类准确率最大化作为优化原则，SVM优化参数模型对应的组合优化形式为：

其中，F(∙)为罚参数C和核参数g的二元函数。

CIALO算法优化SVM参数(C,g)的程序流程见图2，具体操作步骤为：

步骤1数据预处理。为消除数据集不同属性间存在的量纲差异，一般需要对数据集进行标准化（或归一化）等预处理。

步骤2数据集的确定。将预处理后的数据集整理为分析数据集，并确定出SVM的训练集Dtr和预测集Dpr。

步骤3模型参数设置。CIALO算法中需要设置的参数有：最大迭代次数Itermax、搜索体数目（种群规模）Numagent、混沌搜索次数Numchaos和侦查蚁狮比例p0；设置SVM中参数C和g的取值范围。

步骤4种群初始化。CIALO算法中每只蚂蚁和蚁狮均代表SVM二元函数F(C,g)的待优化参数组合(C,g)；根据步骤3中罚参数C和核参数g的取值范围随机初始化蚂蚁和蚁狮种群，以实现Numagent个蚁狮个体的并行搜索。

步骤5计算蚂蚁和蚁狮的适应度值，并确定蚁狮种群。计算每只蚂蚁和蚁狮的适应度值（即对Dpr集的分类准确率），同时将蚂蚁和蚁狮组合并按适应度值降序排序，再将前Numagent个个体赋予给蚁狮种群。

步骤6混沌搜索过程。

（1）计算蚁狮种群中侦查蚁狮的数目Numinv= p0×Numagent；

（2）设置Fuch混沌映射的搜索次数Numchaos；

（3）根据式（1）进行混沌搜索，将得到的混沌变量再利用式（4）映射为优化变量（参数组合(C,g)），即得到侦查蚁狮的新位置；

（4）计算Fuch映射搜索所得侦查蚁狮的适应度值，并与被替换蚁狮的适应度值比较，若优于原适应度值则替换，反之则保持不变；

（5）判断是否达到最大搜索次数Numchaos，若是，则跳转执行步骤7，反之，则混沌搜索次数加1，并跳转执行（3）。

步骤7对蚁狮种群按适应度值重新降序排列，并更新精英Elite：如果蚁狮种群最优个体的适应度值优于精英的，则以该蚁狮替换精英，反之则精英保持不变。

步骤8判断CIALO算法是否达到终止条件，即当前迭代次数是否达到Itermax：若是，则输出精英Elite对应的最优适应度值和参数组合(CElite,gElite)，否则迭代次数加1，并跳转执行步骤5。

Fig.2 Flow chart of CIALO algorithm for optim izingSVM parameters图2 CIALO算法优化SVM参数的流程图

4 实例化分析

为验证CIALO算法优化SVM参数的有效性和可行性，以UCI标准数据库中的8组数据集为实验数据分别进行两组实验：第一组实验是改进算法与其他智能算法的对比实验，以验证CIALO算法优化SVM参数的优越性能；第二组实验是改进算法与基于其他混沌映射的对比实验，以说明基于Fuch映射的CIALO算法优化SVM参数的较好性能。8组实验数据集的属性信息见表1。

Table 1 Attributes information of UCI datasets表1 UCI数据集的属性信息

表1中，IP/YE/WD/BS/3TE/IS/PB/SF2分别表示Ionosphere/yeast/WaveformDatabase/BalanceScale/TicTac-ToeEndgame/ImageSegmentation/PageBlocks/SolarFlare-Data2数据集，训练样本均采用均匀随机选取方式[15]确定，数据集剩余样本作为测试集。

由于数据集的不同属性指标间一般因量纲等差异而影响分类器性能，需要对数据集进行归一化处理，计算公式为：

其中，xmjax和xmjin分别表示第j列的最大值和最小值；xij和Xij分别表示归一化前后样本值。

4.1与其他智能算法的对比实验

本节以遗传算法（GA）、蚁群算法（ACO）和传统ALO算法作为优化SVM参数的对比算法，以验证CIALO算法优化SVM参数的优越性能。

模型中参数的设置情况为：4种算法的最大迭代次数Itermax=150，搜索体数目Numagent=5；CIALO算法中侦查蚁狮占比p0=0.2，混沌搜索次数Numchaos=100；GA算法[7]其他参数设置为：交叉概率pc=0.8，变异概率pm=0.05；ACO算法其他参数设置为：信息素增加强度Q=1，信息素挥发系数Rho=0.8，蚂蚁爬行速度V=0.3；SVM中参数C与g的取值范围分别为(0,10]与(0,1]。

根据GA、ACO、ALO和CIALO算法参数设置情况和表1训练样本设置情况，利用4种算法优化SVM参数模型（分别记作GASVM、ACOSVM、ALOSVM和 CIALOSVM）分别对8组实验数据进行30次实验，评价指标为30次实验的分类准确率均值（mean）、标准差（std）、最大值（max）、最小值（m in）和t-test的p-value。以30次实验平均值作为GASVM、ACOSVM、ALOSVM和CIALOSVM等4种算法的最终结果见表2，绘制的平均分类准确率柱状对比图见图3。

Table 2 Contrast on experiment result of four algorithms表2 4种算法的实验结果对比

Fig.3 Contrast on average accuracy of four algorithms图3 4种算法的平均准确率对比图

由表2可知：GASVM、ACOSVM、ALOSVM和CIALOSVM这4种算法对8组实验数据30次实验的p-value均远远小于0.05，说明4种算法的实验结果均具有较高的显著性，且CIALOSVM算法的p-value最小，表明其具有更高的显著性水平。8组实验数据的统计结果中，CIALOSVM算法均具有最大的平均分类准确率、最小的预测标准差和最大的分类准确率，表明改进算法具有较高的平均预测精度、较好的算法稳定性以及较大的最优分类准确率。同时CIALOSVM算法也具有最大的最小分类准确率（m in指标），说明改进算法即使在最坏极端情况下也具有较优的预测性能，保证了算法在工程应用中的较小错判率，从而有利于降低实际应用中的成本和损失等，具有较好的应用前景。

由图3可知：CIALOSVM算法对8组实验数据的预测分析中具有不同幅度的精度提高，说明改进算法对不同数据集的优化性能是有所差异的。改进算法与其他3种对比算法相比具有最大的平均分类准确率，直观地展示了改进算法的较好收敛精度。

4.2与其他混沌映射的对比实验

本节以Logistic映射和Tent映射作为对比混沌映射，以验证基于Fuch映射的CIALO算法优化SVM参数的较好性能。

相关实验参数设置情况同4.1节，利用基于Logistic、Tent和Fuch映射的3种CIALO算法优化SVM参数模型（分别记作LIALOSVM、TIALOSVM和FIALOSVM）分别对8组实验数据进行30次实验，选用分类准确率、执行时间、达到最大分类准确率的收敛代数和ttest的p-value作为评价指标，以30次实验的平均值作为最终实验结果，见表3。

Table 3 Contrast on experiment result of modified ALO algorithms based on different chaotic mappings表3 基于不同混沌映射的改进ALO算法实验结果对比

由表3可知：LIALOSVM、TIALOSVM和FIALOSVM这3种算法均具有远小于0.05的p-value，表明3种算法对8组实验数据的30次实验结果均具有较高的显著性，且FIALOSVM算法对8组数据集几乎均具有最小的p-value，表明基于Fuch映射的改进算法具有更高的显著性水平。基于3种混沌映射的CIALOSVM算法对8组实验数据的实验结果中，FIALOSVM算法均具有最大的平均分类准确率和最小的执行时间（除IP的mean外），表明FIALOSVM算法与LIALOSVM和TIALOSVM算法相比具有较好的推广泛化性能和较高的迭代寻优效率。

在平均收敛代数指标中，3种算法对8组实验数据各具优势：FIALOSVM和LIALOSVM算法在3个数据集上均具有最小收敛代数，而TIALOSVM算法在2个数据集上有最小收敛代数，且3种算法的平均收敛代数都在10代以内。因此在实际应用中可以通过设置相对较小的最大迭代次数以减少算法的执行时间，在一定程度上提高算法的应用价值。

5 结束语

针对传统ALO算法中存在适应度较差的蚁狮个体，从而影响蚁狮种群的整体优良性和算法的寻优性能问题，通过引入侦查机制和混沌搜索策略等措施提出了带混沌侦查机制的蚁狮优化算法，并将其用于SVM参数的优化选择中。数值实验结果表明，改进算法优化SVM参数模型具有较高的平均分类准确率和统计显著性水平、较好的算法稳定性以及最大的最优分类准确率，在一定程度上验证了改进算法在SVM参数寻优中的有效性和可行性。此外，ALO算法作为一种新近提出的智能优化算法还有许多改进的方向，例如选择蚁狮的方式，蚂蚁随机游走的策略和蚂蚁学习率随迭代次数的动态改变等。

References:

[1] M irjalili S. The ant lion optim izer[J]. Advances in Engineering Software, 2015, 83: 80-98.

[2] Vapnik V. The nature of statistical learning theory[M]. New York: Wiley, 1998.

[3] Danenas P, Garsva G. Selection of support vector machines based classifiers for credit risk domain[J]. Expert Systems w ith Applications, 2015, 42(6): 3194-3204.

[4] Jedliński Ł, Jonak J. Early fault detection in gearboxes based on support vector machines and multilayer perceptron w ith a continuous wavelet transform[J]. Applied Soft Computing, 2015, 30: 636-641.

[5] Yang Dalian, Liu Yilun, Li Songbai, et al. Gear fault diagnosis based on support vector machine optim ized by artificial bee colony algorithm[J]. Mechanism and Machine Theory, 2015, 90: 219-229.

[6] Wauters M, Vanhoucke M. Support vector machine regression for project control forecasting[J]. Automation in Construction, 2014, 47: 92-106.

[7] Sajan K S, Kumar V, Tyagi B. Genetic algorithm based support vector machine for on-line voltage stability monitoring[J]. International Journal of Electrical Power & Energy Systems, 2015, 73: 200-208.

[8] Yuan Rongdi, Peng Dan, Feng Huizong, et al. Fault diagnosis for engine by support vector machine and improved particle swarm optim ization algorithm[J]. Journal of Information and Computational Science, 2014, 11(13): 4827-4835.

[9] Sun Wei, Liu Xuan. The safety assessment of power information system w ith particle swarm optim ization based support vector machine[J]. Journal of Information and Computational Science, 2014, 11(14): 4921-4929.

[10] Zhang Xiaoli, Chen Wei, Wang Baojian, et al. Intelligent fault diagnosis of rotating machinery using support vector machine w ith ant colony algorithm for synchronous feature selection and parameter optimization[J]. Neurocomputing, 2015, 167: 260-279.

[11] Acevedo J, Maldonado S, Lafuente S, et al. Model selection for support vector machines using ant colony optim ization in an electronic nose application[M]//Ant Colony Optimization and Swarm Intelligence. Berlin, Heidelberg: Springer, 2006: 468-475.

[12] Samadzadegan F, Hasani H, Schenk T. Simultaneous feature selection and SVM parameter determination in classification of hyperspectral imagery using ant colony optimization[J]. Canadian Journal of Remote Sensing, 2012, 38(2): 139-156. [13] Gham isi P, Benediktsson J A. Feature selection based on hybridization of genetic algorithm and particle swarm optimization[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(2): 309-313.

[14] Fu Wenyuan, Ling Chaodong. An adaptive iterative chaos optimization method[J]. Journal of Xi’an Jiaotong University, 2013, 47(2): 33-38.

[15] Gao Leifu, Zhao Shijie, Gao Jing. Application of artificial fish-swarm algorithm in SVM parameter optim ization selection[J]. Computer Engineering and Applications, 2013, 49 (23): 86-90.[16] Horton P, Nakai K. A probabilistic classification system for predicting the cellular localization sites of proteins[C]// Proceeding of the 4th International Conference on Intelligent Systems for Molecular Biology, St Louis, USA, 1996. Menlo Park, USA:AAAI, 1996: 109-115.

附中文参考文献：

[14]傅文渊,凌朝东.自适应折叠混沌优化方法[J].西安交通大学学报, 2013, 47(2): 33-38.

[15]高雷阜,赵世杰,高晶.人工鱼群算法在SVM参数优化选择中的应用[J].计算机工程与应用, 2013, 49(23): 86-90.

ZHAO Shijie was born in 1987. He is a student w ith M.S.-Ph.D. continuous study at Liaoning Technical University, and the student member of CCF. His research interests include artificial intelligence, data mining, optimization and management decision, etc.

赵世杰（1987—），男，山东五莲人，辽宁工程技术大学硕博连读研究生，CCF学生会员，主要研究领域为人工智能，数据挖掘，优化与管理决策等。

GAO Leifu was born in 1963. He received the Ph.D. degree in engineering mechanics from Liaoning Technical University in 2006. Now he is a professor and Ph.D. supervisor at Liaoning Technical University. His research interests include optim ization theory and application, nonlinear dynamic system, etc.

高雷阜（1963—），男，辽宁阜新人，2006年于辽宁工程技术大学工程力学专业获得博士学位，现为辽宁工程技术大学理学院优化与决策研究所教授、博士生导师，主要研究领域为最优化理论与应用，非线性动力系统等。发表学术论文80余篇，主持和参与国家自然科学基金、教育部博士点基金、辽宁省自然科学基金、辽宁省教育厅基金等项目。

YU Dongmei was born in 1986. She is a Ph.D. candidate at Liaoning Technical University. Her research interest is optimization theory and application.

于冬梅（1986—），女，辽宁鞍山人，辽宁工程技术大学博士研究生，主要研究领域为最优化理论与应用。

TU Jun was born in 1982. He received the Ph.D. degree from College of Information Science and Engineering, Northeastern University in 2014. Now he is a lecturer at College of Science, Liaoning Technical University. His research interest is intelligent algorithm.

徒君（1982—），男，安徽全椒人，2014年于东北大学信息科学与工程学院获得博士学位，现为辽宁工程技术大学理学院讲师，主要研究领域为智能算法。

Ant Lion Optim izer w ith Chaotic Investigation M echanism for Optim izing SVM Parametersƽ

ZHAO Shijie+, GAO Leifu, YU Dongmei, TU Jun
Institute of Optim ization and Decision, Liaoning Technical University, Fuxin, Liaoning 123000, China + Corresponding author: E-mail: zhao2008shijie@126.com

Key words:ant lion optim izer; chaos; investigation mechanism; support vector machine; parameter optimization

Abstract:As ant lion optim izer (ALO) is a new bionic intelligence algorithm, there are a number of respects on the improvement and development. Since antlion’s population (species) has some poor-fitness individuals in basic ALO algorithm, the behavior of ants selecting those antlions for random walk w ill result in increasing the possibility of its trapping into local optima and impacting on the algorithm’s optimal performance. Considering this question, this paper proposes ant lion optim izer w ith chaotic investigation mechanism (CIALO), which draws experience from the investigation idea of artificial bee colony algorithm (ABC) and brings in chaos search mechanism based on the original information of antlions. The CIALO algorithm firstly defines poor-fitness individuals of the sorted antlions’population as investigative ant lions (IAL). Meanwhile, the original position information of these antlions is regarded as the initial value of Fuch chaotic mapping. Then it can gain a better-much position by a certain number of chaos search iteration and reassigns the position to IAL, which is beneficial to improve the superiority of antlion’s population and the optimal performance of the algorithm. Eventually, the CIALO algorithm is used to optim ize the parameters of support vector machine (SVM). The public datasets from University of California Irvine (UCI) is employed for evaluating the
proffered algorithm. The experimental results imply that the CIALO algorithm for optimizing SVM parameters has stronger optimal performance and better stability of the algorithm.

doi:10.3778/j.issn.1673-9418.1506093 E-mail: fcst@vip.163.com

文献标志码：A

中图分类号：TP18