On a Quasilinear Elliptic Equation with Superlinear Nonlinearities∗

Gao JIALina HUANGXiaojuan ZHANG

1 Introduction

Let Ω∈RN(N≥1)be open(possibly unbounded)and consider a weak solution in(see Section 2)to the following quasilinear elliptic problem:

whereλj0is thej0th eigenvalue ofL((2.3)below)of multiplicityJ0,andQis a singular quasilinear elliptic operator defined by

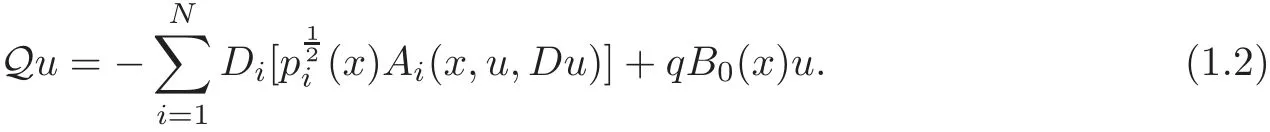
The nonlinear partf(x,u)in(1.1)satisfies certain superlinear conditions.

In fact,there have been many results about quasilinear elliptic equations,under the conditions of which the nonlinearities satisfy sublinear or linear growth in weighted Sobolev spaces.One can refer to[1–8].For example,Shapiro[7]investigated the problem(1.1)aiming at the first eigenvalueλ1whose corresponding eigenfunction space has better characters with superlinear nonlinearities.In[8],Jia and Huang proved the existence of solutions to elliptic equations similar to(1.1)for the semilinear operator with superlinear nonlinearities.Compared with the previous work,this paper is supposed to gain an existence result of(1.1)for any eigenvalueλj0(j0≥1),where the nonlinearties of quasilinear elliptic equations satisfy certain superlinear growth conditions.Therefore we have to overcome the difficulties that the eigenvalueλj0may be of multiplicityJ0and that the corresponding eigenfunctions may be sign-changing.

(1.1)is one of the most useful sets ofp-Laplacian equations(see[9]).In fact,there are some serious ones.It appears that certain nonlinear mathematical models lead to differential equations with thep-Laplacian.One of them describing the behavior of compressible fl uid in a homogeneous isotropic rigid porous medium is presented below.But some purely mathematical properties of thep-Laplacian also seem to be a challenge for nonlinear analysis and their study leads to the development of new methods and approaches.

Our main ideas prove the existence of{un}in the finite dimensional spaceSnspannedvia Brouwer’s fixed point theorem at first.Then we obtain the uniform boundedness of{un}under the norm ofby virtue of a new compactly embedding theorem established by Shapiro in[7].Finally,by the projective technique,the conclusion for existence of solutions to(1.1)inSncould be extended toTo overcome the difficulties brought byλj0,■-relationship is put forward in Definition 2.3 between the operatorsQandL,which is different from[7]and[8].

This paper is organized as follows.In Section 2,we introduce some necessary assumptions and the main results.In Section 3,four fundamental lemmas are established.In Section 4,the proofs of main results are given.Section 5 illustrates an example to cover Definition 2.3.

2 Assumptions and Main Results

In this section,we introduce some assumptions and give the main results in this paper.

Let Γ⊂∂Ω be a fixed closed set(it may be an empty set)andbe weight functions.q(x)is nonnegative(maybe identically zero).Denote byp(x)the vector function

Consider the following pre-Hilbert spaces

Definition 2.2(Ω,Γ)is a new-VLregion if the following conditions

(VL-1)There exists a complete orthonormal systemRemark 2.3 Observing that foris a positive function,meets both(f-2)and(f-3).

Now we state our main results in this paper.

To derive out Theorem 2.1,we first discuss the problem inSnwhich is the subspace ofspanned byϕ1,···,ϕn.Then by virtue of Galerkin method,the results will be extended to

3 Fundamental Lemmas

In this section,we introduce and establish four fundamental lemmas.Lemmas 3.1–3.2 give two useful embedding theorems.Lemma 3.3 constructs some approximation solutions inSn.Lemma 3.4 studies the properties of the approximation solutions.

whereTmis a positive constant depending onm.

The remaining proof is separated into two parts.The first part is to prove the claim(3.6)forfm(x,s).The second part is to get the conclusion by leavingm→∞based on(3.6).

Similarly we can also obtain the same conclusion,where−m≤s≤mors≤−m.As a result,

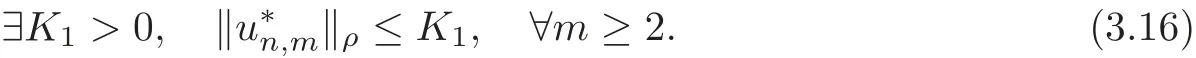
(3.3)and(3.16)imply that there is a subsequence of(for easy notation,take the full sequence)and a(see[12])such that

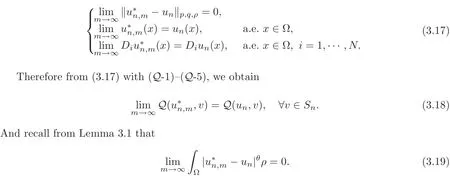
Now replacingmbymjin(3.6)and taking the limit asj→∞on both sides of the equation,we consequently obtain that(3.1)holds and Lemma 3.3 is established.

Lemma 3.4Let all the assumptions in Theorem2.1hold.Then the sequence{un}obtained in Lemma3.3is uniformly bounded in

Based on Lemma 3.3 andrelationship,for the proofs of Lemma 3.4,one can refer to[7]or[8].

4 Proof of Theorem 2.1

Sinceis a separable Hilbert space,from Lemmas 3.1–3.2,we conclude that there exists a subsequence of(for easy notation,we take the full sequence)and a functionwith the following properties(see[12]):

Observing(Q-4)and(Q-5),we have that the integrand in(4.15)is nonnegative almost everywhere in Ω.Hence the integrand in(4.15)converges to zero inL1(Ω).However,from[13],we have a subsequence of the integrand converging to zero almost everywhere in Ω.And from(4.3),converges to zero almost everywhere in Ω.We conclude that(4.8)is indeed true.So it remains to establish(4.14).

Recall Lemma 3.1,Lemma 3.4 and(4.17),clear from(4.17)thatTherefore(4.20)holds and hence(4.8)is established.

Secondly,to establish(4.9),set Ω1to be the set meeting the following three conditions simultaneously:

Now we have that(4.8)–(4.9)hold which will imply(4.7).Let Ω2be the subset of Ω,where(Q-1),(Q-4),(4.8)and(4.9)hold simultaneously.Consequently,

Suppose that there existssuch that(4.7)does not hold.Hence by(4.9)there exists a further sequence

Observingand(4.8),the limit on the left side of(4.31)is zero.But from(Q-4),the right side of(4.31)is strictly greater than zero,which has led to a contradiction.Hence(4.7)holds at every point in Ω2,and consequently by(4.26),it holds almost everywhere in Ω.So the statement(4.7)is fully established.

Step 2 We proceed with the proof and letvJ∈SJ,whereJ≥j0+J0is a fixed but arbitrary positive integer.From(4.3),(4.7)and(Q-1)we can get

5 An Example forrelated

Now we give an example ofQwhich isrelated toL.

TakeN=1,Ω =(−1,1),Γ =the empty set,From the definition ofL,we get

whereK4is a constant.

ThatQisrelated toLthen follows immediately from this last inequality.

[1]Berestycki,H.and Figueredo,D.G.,Double resonance in semilinear elliptic problems,Communications in Partial Differential Equations,6,1981,91–120.

[2]Rumbos,A.and Shapiro,V.L.,Jumping nonlinearities and weighted Sobolev spaces,Journal of Differential Equations,214,2005,326–357.

[3]Rumbos,A.,A semilinear elliptic boundary value problem at resonance where the nonlinearity may grow linearly,Nonlinear Analysis TMA,16,1991,1159–1168.

[4]Lefton,L.and Shapiro,V.L.,Resonance and quasilinear parabolic differential equations,Journal of Differential Equations,101,1993,148–177.

[5]Shapiro,V.L.,Resonance,distributions and semilinear elliptic partial differential equations,Nonlinear Analysis TMA,8,1984,857–871.

[6]Jia,G.and Zhao,Q.,Existence results in weighted Sobolev spaces for some singular quasilinear elliptic equations,Acta Applicandae Mathematicae,109,2010,599–607.

[7]Shapiro,V.L.,Singular Quasilinearity and Higher Eigenvalues,Memoirs of the American Mathematical Society,Providence,Rhode Island,726,2001.

[8]Jia,G.,Huang,L.N.and Zhang,X.J.,Existence of solutions for quasilinear elliptic equations with superlinear nonlinearities,Boundary Value Problem,90,2012,1–13.

[9]Kufner,A.and Sandig,A.,Some Applications of Weighted Sobolev Spaces,Teubner-Texte zur Mathematik,Prague,Czechoslovakia,1987.

[10]Shapiro,V.L.,Special functions and singular quasilinear partial differential equations,SIAM J.Math.Anal.,22,1991,1411–1429.

[11]Kesavan,S.,Topics in Functional Analysis and Applications,John Wiley and Sons,New York,1989.

[12]Xuan,B.J.,Variational Methods,University of Science and Technology of China Press,Hefei,2006.

[13]Rudin,W.,Real and Complex Analysis,McGraw-Hill,New York,1974.

[14]Courant,R.and Lazer,A.C.,Methods of Mathematical Physics,Vol.1,John Wiley,New York,1966.