On the Existence for Some Special Primitive Elements in Finite Fields∗
Qunying LIAO Jiyou LI Keli PU
1 Introduction and Background
Let Fqbe a finite field of characteristicpand orderq.fixedn-extension of Fq.An elementα∈Fqnis called normal overis a basis of Fqnover Fq,called a normal basis.Normal bases are important in efficient arithmetic computation for finite fields and have many applications in coding theory and cryptography(see[16–17]).The basic facts on normal bases of finite fields are collected in the book[16].
An elementα∈Fqnis called primitive if it is a generator of the multiplicative groupIt is a central problem in computational number theory to construct a primitive element in a ifnite field.However,even determining a primitive element in a finite field is hard.Primitive elements over finite fields are discussed by Carlitz[1],Davenport[10],et al.,and are widely used in cryptography system,coding theory and design theory.
An element is called primitive normal if it is both primitive and normal.The normal basis generated by a primitive normal element is called a primitive normal basis.For anyα∈Fqn,f(x)∈Fq[x]represents the monic minimal polynomial ofαover Fq.f(x)is said to be a primitive or normal polynomial over Fqifαis primitive or normal respectively.f(x)is called a primitive normal polynomial over Fqwhenαis a primitive normal element over Fq.
The combination of primitivity and normality was first studied by Carlitz[1].By using properties for the additive character of Fqn,he proved that there are at most finitely many pairs(q,n)of finite fields,for which there does not exist an element in Fqnthat is both primitive and normal over Fq.He also proved in[1–2]that for all sufficiently largeqn,there exists a primitive normal elements ofoverFq.In the case where the cardinalityqis prime,the existence of a primitive normal element was proved by Davenport[10].For the general case,by improving the method of Carlitz and Davenport,which handles all but finitely many pairs(q,n),Lenstra and Schoof[15]affirmatively settled the existence of primitive normal elements for all finite fields extensionsand proved the following well-known primitive normal basis theorem.
Theorem 1.1(see[15])For any n≥1and any prime power q,there is a primitive normal element inoverFq.
For a different proof of this theorem,see Cohen and Huczynska[8].Cohen and Hachenberger[7]strengthened the primitive normal basis theorem of Lenstra and Schoof[15]and the theorem of Cohen on primitive elements with prescribed trace(see[6]).It established the conjecture of Morgan and Mullen[18],who,by means of a computer search,verified the existence of such elements for the cases in whichq≤97 andn≤6,nbeing the degree of.Apart from two pairs(q,n),Cohen and Hachenberger[7]settled the conjecture purely theoretically and proved the following theorem.
Theorem 1.2(see[7])For any n≥1,any prime power q and any nonzero element c inFq,there exists a primitive normal element α∈such thatTr(α)=c,whereTris the trace map from
In recent years,some further improvements of the primitive normal basis theorem are given(see[11–13]).
It is also interesting to note that Chou and Cohen[3]resolved completely the question whether there exists a primitive elementsuch that bothαand its reciprocalα−1have zero trace overFq.Trivially,there was no such element whenn<5,and they established the existence for all pairs(q,n)(n≥5)except(4,5),(2,6)and(3,6).In recent years,Fan and Cohen,et al.[9,19]further proved that for any prime powerqand any integern≥2,there is an elementsuch that bothαandα−1are primitive normal overFqexcept when(q,n)is one of the pairs(2,3)–(2,4),(3,4),(4,3)and(5,4).Equivalently,with the same exceptions,there is always a primitive polynomialp(x)of degreenoverFqwhose coefficients ofxand ofxn−1are both zero.Their method employed Kloosterman sums and a sieving technique.
For convenience,throughout this paper we denoteω(n)to be the number of distinct prime factors of the integern>1.
In 2006,Tian and Qi[19]proved that there exists a primitive elementsuch that bothαandα−1are normal elements ofwhenn≥32.Recently,Wang,et al.[21]gave a sufficient condition on the existence ofαsuch thatαandα+α−1are both primitive or primitive normal for the case 2|q.In the present paper,by using the index sum method we generalize their results to the case thatqis any prime power and prove the following main results.
Theorem 1.3Let q,n be positive integers such thatgcd(n,q)=1andand then there existssuch that αand α+α−1are both primitive,where ω(qn−1)is the number of distinct prime divisors of qn−1.
Corollary 1.1Let q and n be positive integers such thatgcd(n,q)=1.If n≥13and t≥4,then(q,n)∈U1.
Theorem 1.4Let q and n be positive integers such thatgcd(n,q)=1.Suppose that,andso then there exists such that α is primitive normal and α+α−1is primitive,whereis the Euler function of the polynomial xn−1.
2 Preliminaries
In this section,some necessary definitions and lemmas are given.


3 Proofs of the Main Results
Proof of Theorem 1.3 DenotePto be the set of primitive elements ofto be the set of normal elements ofover Fq.De fi neBy Definition 2.1 and(2.2)one has
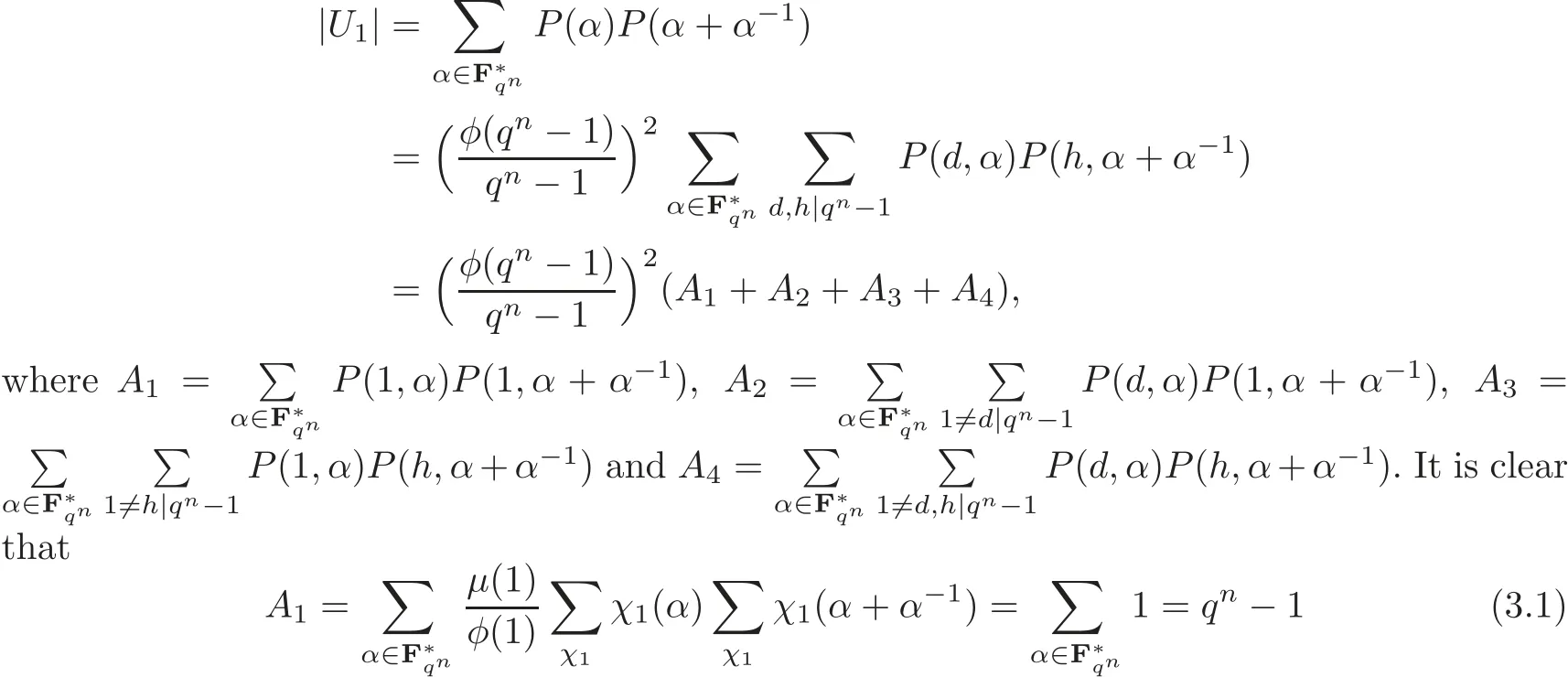

Now we computeA4:

The last inequality follows from Lemma 2.5 and thus

Proof of Corollary 1.1 By(2.4)we have

Example 3.1 Letp=3,whenq<32,that is,t≤3.We can find the(q,n)such that(q,n)∈U1.


4 Concluding Remark
For the setUi(i=1,2),Wang,et al.considered the case thatqis a power of 2.In this paper,we consider the general case and obtain the similar estimate.By the same proof of our main results,one can get a sufficient condition for the setto be not empty,which is left to readers.
In fact,the main difference between the proofs in[21]and the present paper is to computeIn detail,the key is to estimate the value ofThis can be reduced to the Jacobi sumin the case 2|q,which can be bounded by using the techniques of Jacobi sums.In the case thatqis odd,this approach does not work.In[21]the authors pointed out that similar results could be obtained through certain slight modifi cation.To make it more exact,the difficulty of estimating the related exponential sums could be overcome to obtain similar results in finite fields with general characteristics.In this paper,we completely solve the problem and our proof looks briefer than that in[21]by using the Weil’s character sum estimate(see[20]).With our method,all results in[21]for the case 2|qcan be paralleled to the general case.For the time being,we omit it here and leave it to readers.
AcknowledgementThe authors would like to thank the reviewers for some helpful suggestions.
[1]Carlitz,L.,Primitive roots in finite fields,Trans.Am.Math.Soc.,73,1952,373–382.
[2]Carlitz,L.,Some problems involving primitive roots in a finite field,Proc.Nat.Acad.Sci.U.S.A.,38,1952,314–318.
[3]Chou,W.S.and Cohen,S.D.,Primitive elements with zero traces,Finite Fields Appl.,7,2001,125–141.
[4]Cohen,S.D.,Primitive elements and polynomials:Existence results,Lecture Notes in Pure and Appl.,http://www.researchgate.net/publication/265461791
[5]Cohen,S.D.,Primitive roots in the quadratic extension of a finite field,J.London Math Soc.,27(2),1983,221–228.
[6]Cohen,S.D.,Primitive elements and polynomials with arbitrary trace,Discrete Math.,83,1990,1–7.
[7]Cohen,S.D.and Hachenberger,D.,Primitive normal bases with prescribed trace,Applicable Algebra in Engineering Communication and Computing,9,1999,383–403.
[8]Cohen,S.D.and Huczynska,S.,Primitive free quartics with specifi ed norm and trace,Acta Arith.,109(4),2003,359–385.
[9]Dahab,R.,Hankerson,D.,Hu,F.,et al.,Software multiplication using Gaussian normal bases,IEEE Trans.Comput.,55,2006,974–984.
[10]Davenport,H.,Bases for finite fields,J.London Math.Soc.,43,1968,21–39.
[11]Fan,S.Q.,Han,W.B.,Feng,K.Q.and Zhang,X.Y.,Primitive normal polynomials with the first two coefficients prescribed:A revisedp-adic method,Finite Fields Appl.,13(3),2007,577–604.
[12]Fan,S.Q.,Han,W.B.and Feng,K.Q.,Primitive normal polynomials with multiple coefficients prescribed:An asymptotic result,Finite Fields Appl.,13(4),2007,1029–1044.
[13]Fan,S.Q.,Primitive normal polynomials with the last half coefficients prescribed,Finite Fields Appl.,15(5),2009,604–614.
[14]He,L.B.and Han,W.B.,Research on primitive elements in the formα+α−1over Fq,Journal of Information Engineering University,4(2),2003,97–98(in Chinese).
[15]Lenstra,H.W.Jr.and Schoof,R.J.,Primitive normal bases for finite fields,Math.Comp.,48,1987,271–231.
[16]Lidl,R.and Niederreiter,H.,Finite Fields,Cambridge University Press,Cambridge,1987.
[17]Lidl,R.and Niederreiter,H.,Finite Fields and Their Applications,2nd edition,Cambrige University Press,Cambrige,1994.
[18]Morgan,I.H.and Mullen,L.G.,Primitive normal polynomials over finite fields,Math.Comp.,63,1994,759–765.
[19]Qi,W.F.and Tian,T.,Primitive normal element and its inverse in finite fields,Acta Mathematics Sinica(Chinese Series),49(3),2006,657–668.
[20]Wan,D.Q.,Generators and irreducible polynomials over finite fields,Mathematics of Computation,66,1997,1195–1212.
[21]Wang,P.P.,Cao,X.W.and Feng,R.Q.,On the existence of some specifi c elements in finite fields of characteristic 2,Finite Fields Appl.,18(4),2012,800–813.
 Chinese Annals of Mathematics,Series B2016年2期
Chinese Annals of Mathematics,Series B2016年2期
- Chinese Annals of Mathematics,Series B的其它文章
- On a Quasilinear Elliptic Equation with Superlinear Nonlinearities∗
- Approximate Controllability of Neutral Functional Differential Systems with State-Dependent Delay∗
- Analytic Feynman Integrals of Functionals in a Banach Algebra Involving the First Variation∗
- On the Number of Limit Cycles in Small Perturbations of a Piecewise Linear Hamiltonian System with a Heteroclinic Loop∗
- A Parameterization of the Canonical Bases of Affine Modified Quantized Enveloping Algebras∗
- Approximate Representation of Bergman Submodules∗
