Approximate Controllability of Neutral Functional Differential Systems with State-Dependent Delay∗

Xianlong FU Jialin ZHANG

1 Introduction

In this paper,we consider the approximate controllability of systems represented in the following semilinear neutral functional differential systems with state-dependent delay:

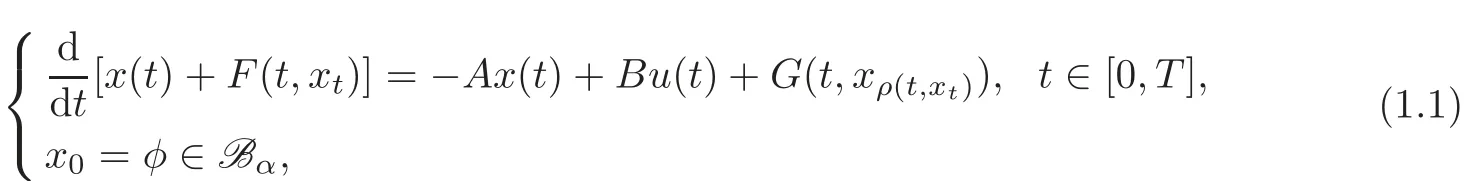
where the state variablex(·)takes values in a Hilbert spaceXand the control functionu(·)is given in the Banach spaceL2([0,T];U),whereUis also a Hilbert space.Bis a bounded linear operator fromUintoX.The(unbounded)linear operator−A:D(−A)→Xgenerates an analytic semigroupare appropriate functions to be specified later.is a phase space given in the next section.The notationxtrepresents the history function defined by,and belongs to some abstract phase spacedescribed axiomatically andis a continuous function.

The controllability theory for abstract linear control systems in an in finite-dimensional space is well-developed,and the details can be found in various papers and monographs(see[4,16]and references therein).Several authors have extended the controllability concepts to in finitedimensional systems represented by nonlinear evolution equations(see[20–21,35]).Most of the controllability results for nonlinear in finite-dimensional control systems concern the socalled semilinear control system that consists of a linear part and a nonlinear part.Zhou[35]studied approximate controllability of an abstract semilinear control system by assuming certain inequality conditions that are dependent on the properties of the system components.Naito[20–21]studied the approximate controllability of the same system.He showed that under a range condition on the control action operator,the semilinear control system is approximately controllable.Jeong et al.[14]and Wang[30]have extended the result to retarded systems with finite delays.Yamamoto and Park[32]discussed the same problem for parabolic equations with a uniformly bounded nonlinear part.Do[6],Joshi and Sukavanam[15]discussed approximate controllability for a class of semilinear abstract equations,while Muthukumar and Rajivganthi[19]investigated the controllability problem for a stochastic nonlinear third-order dispersion equation.

Bashirov and Mahmudov[2]showed that under an appropriate condition on resolvent operators,the approximate controllability of semilinear systems is implied by the approximate controllability of its linear part.This resolvent condition is convenient for application and it has been used in many papers to study the approximate controllability for nonlinear(functional)differential equations(see,for instance,[5,8,24–25]).In[5],by using the Schauder fixed point theorem and the resolvent condition,Dauer and Mahmudov studied the approximate controllability and complete controllability for the following semilinear abstract control system with finite delay:

In[9,18,24–27,33–34],the authors investigated the approximate controllability for semilinear impulsive systems and fractional order(stochastic)differential systems with(state-department)delay also by using the resolvent condition.

On the other hand,neutral partial functional differential systems appear in a great many practical mathematical models,such as some structured population models and systems of lossless transmission line networks(see[11,31]).In recent years,existence results,asymptotic properties and controllability on this type of systems have been investigated by many authors(see[3,7,12]).We are going to discuss the approximate controllability for neutral partial functional differential systems with state-dependent delay.State-dependent delay differential equations can be met in various practical models.Some recent applications can be found in[1,17].In particular,the approximate controllability of fractional functionals and integrodifferential equations with state-dependent delay has been studied in[24,26,33–34].

A motivation of the present paper is the approximate controllability problem of the following neutral partial differential control systems:

System(1.3)arises as a model for nonlinear heat fl ow in materials with fading memory.Herez(t,x)represents the temperature of a conduct of the pointxand timet.Evidently,this system can be treated as the abstract equation(1.1),however,the results established in[5,24–25]become invalid for this situation,since the functionsf,gin(1.3)involve spatial derivatives.In fact,as one will see in Section 4,if we takethen the third variables offandgare defined onand so the solutions can not be discussed onXlike in[24–25].

In this paper,inspired by the work in[7,28–29],we shall discuss this problem by using the fractional power operators theory andα-norm techniques,that is,we shall restrict this equation in a Banach spaceXα(⊂X)induced by fractional power operators.We first present the induced phase spacefor in finite delay,through which we investigate the existence of mild solutions and then we obtain the approximate controllability for(1.1)in spaceX.In this manner we overcome the above mentioned difficulty successfully and the achieved controllability results can be applied to the systems involving spatial derivatives(see the system(4.1)in Section 4).Hence our obtained results are more general in applications than those of[5,24–25].In addition,it can be seen that our techniques can also be adopted to study the approximate controllability of other kinds of control systems(such as fractional order and stochastic systems with in finite delay)to improve the existing results in,for instance,[9,26,33–34].We would also like to point out here that the resolvent condition(H0)employed in this paper is verifi ed readily as shown in the example in Section 4,which is more advantageous than the range condition used in[14,30],since it seems difficult to be verifi ed for in finitely delayed control systems.

The whole article is organized as follows:We initially present some preliminaries about analytic semigroups and phase spaces for in finite delay in Section 2.Particularly,to make them still valid in our situation,we introduce the axioms of phase spaces on the spaceXα.In Section 3,we first discuss the existence of mild solutions for System(1.1)by applying the fixed point theorem,and then we study the approximate controllability of(1.1)using limit arguments.Finally,in Section 4,an example is provided to show the applications of the obtained results.

2 Preliminaries

Throughout this paper,Xis a Hilbert space with normin finitesimal generator of a compact analytic semigroupof uniformly bounded linear operators.Let 0∈ ρ(A).Then it is possible to define the fractional power,for 0＜α ≤1,as a closed linear operator on its domain.Furthermore,the subspaceD(Aα)is dense inXand the expression

defines a norm onHereafter we denote bythe Banach spacenormed withThen for eachα＞0,Xαis a Banach space,and the imbedding is compact whenever the resolvent operator ofAis compact.

For the analytic semigroup,the following properties will be used(see[22]):There exist constantssuch that,fort∈[0,T],

To study the system(1.1),we assume that the historiesbelong to some abstract phase spacewhich is defined axiomatically.In this article,we employ an axiomatic definition of the phase spaceintroduced by Hale and Kato[10]and follow the terminology used in[13].Thus,will be a linear space of functions mapping(−∞,0]intoXendowed with a seminormWe assume thatsatisfies the following axioms:

(A)Ifis continuous onthen for everyt∈[σ,σ+a)the followings hold:

(i)

(ii)

(iii)

HereH≥0 is a constant,is continuous andM(·)is locally bounded,andH,K(·),M(·)are independent ofx(t).

(A1)For the functionx(·)in(A),xtis acontinuous function on[σ,σ+a].

(B)The spaceis complete.

We denote bythe set of all the elements inthat takes values in spaceXα,that is,

Thenbecomes a subspace ofendowed with the seminormwhich is induced bythroughMore precisely,for anythe seminormis defined byinstead ofFor example,let the phase spacer≥0,1≤p＜∞(see[13]),which consists of all classes of functionssuch thatφis continuous on[−r,0],Lebesgue-measurable,andis Lebesgue integrable onis a positive Lebesgue integrable function.The seminorm inis defined by

See also the spacepresented in Section 4.Hence,sinceXαis still a Hilbert space,we will assume that the subspacealso satisfies the following conditions:

Ifis continuous on[σ,σ+a)(inα-norm)andthen for everyt∈[σ,σ+a)the followings hold:

(i)xtis in

(ii)

(iii)HereH,K(·)andM(·)are as in(A)(iii)above.

For the functionx(·)in(continuous function on[σ,σ+a].

The spaceis complete.

For anythe notationrepresents the functionThen,if the functionx(·)in axiomwe may extend the mappingt→xtto the whole interval(−∞,T]by settingxt=φtast≤0.On the other hand,for the functionρ:[0,T]×Bα→(−∞,T],we introduce the set

Then we have the following lemma,which plays an important role in our proofs in the next section.

The mild solution to(1.1)expressed by the semigroup is defined as the following definition.

We shall study the approximate controllability for(1.1)by applying the results established in[2].For this purpose,we need to introduce the following relevant operator:

From Theorem 2 of[2],the hypothesis(H0)is equivalent to the fact that the following linear control system

is approximately controllable on[0,T].

We now end this section by stating some well-known theorems which will be used in the next section.

Theorem 2.1(Lebesgue′s Dominated Convergence Theorem)Letbe a sequence in space L1(Ω,X).Suppose that the sequence converges almost everywhere to a function f and is dominated by some function g∈L1(Ω,X)in the sense thatfor all n∈Nand almost all points x∈Ω.Then f∈L1(Ω,X)and

(iii)for any t∈[a,b],the set{f(t):f∈F}is relatively compact in X.

Then F is relatively compact in space C([a,b];X).

Theorem 2.3(see[23])Let P be a condensing operator on a Banach space X,i.e.,P is continuous and takes bounded sets into bounded sets,and α(P(B))≤α(B)for every bounded set B of X with α(B)＞0.If P(H)⊂H for a convex,closed and bounded set H of X,then P has a fixed point in H(where α(·)denotes Kuratowski’s measure of non-compactness).

3 Approximate Controllability

In this section we discuss the approximate controllability for(1.1).We firstly show that,for anyxT∈X,by choosing proper controluλ(for any givenλ∈(0,1)),there is a mild solutionto(1.1),and then we prove thatxλ(T)→xTinX.

To guarantee the existence of mild solutions,we impose the following restrictions on(1.1).Assumeα∈(0,1).

(H1)B∈L(U,X),i.e.,Bis a bounded linear operator fromUtoX.Let‖B‖=N.

(H2)The functionF:[0,T]×Bα→D(Aα+β)is a continuous function for someβ∈(0,1)withα+β ≤1,and there existsL＞0 such that the functionAβFsatisfies

for any 0≤s1,s2≤T,φ1,φ2∈Bα.Moreover,there existL1＞0 andγ1∈(0,1)such that the inequality

At first we prove the following theorem.

Theorem 3.1Let φ∈Bα.Suppose that assumptions(H0)–(H3)are satisfied.Then for each0＜λ＜1,the equation(1.1)admits one mild solution on(−∞,T]provided that

Then,the assertion that(1.1)admits a mild solution is equivalent to the fact that the operatorQλhas a fixed point.Obviously,the fact that the operatorQλhas a fixed point is equivalent to thathas a fixed point.Next we prove thatPλhas a fixed point by using Theorem 2.1.For this purpose,we will show thatPλmapsB(r)into itself,andverifies a contraction condition whileis a completely continuous operator.

Step 1 For 0＜λ＜1,there exists anr(λ)＞0,such thatIf this is not true,then,for everyr＞0,there existz∈B(r)andt∈[0,T]such thatThen,noting that(by(2.1)–(2.2)andH2),

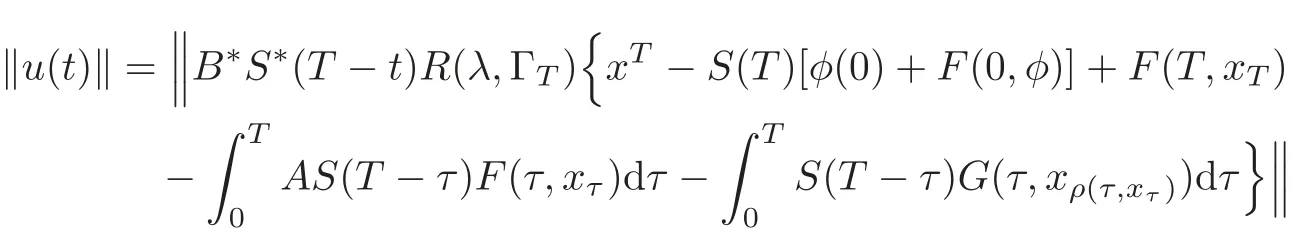
whereK1,K2,K3＞0 are constants independent ofr.Thus,

However,the left side of(3.7)may go to+∞as long asr→+∞sinceγ1,γ2＜1 by our assumption.This is an contradiction.Therefore,there is anr(λ)＞0 such thatPλmapsB(r)into itself.

Step 2 To prove thatsatisfies a contraction condition,we takez1,z2∈B(r),and then,for eacht∈[0,T],by axiom

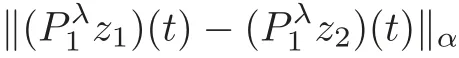
and so from(3.6)satisfies the contraction condition.

Step 3 In order to prove that the operatoris completely continuous,we firstly show that it is continuous onB(r).

Letbe a sequence inB(r)such thatand then,we have thatfor everyThen for all

Step 4 We show that the operatormapsB(r)into a relatively compact subset ofC([0,T];Xα).Firstly,we prove that the setis relatively compact inXαfor everyt∈[0,T].Indeed,the case whent=0 is trivial.Now lett∈(0,T]be fixed,and then

which implies thatis bounded inX.Hence we infer thatV(t)is relatively compact inXαby the compactness of operator(the imbeddingis compact).Hence for eacht∈[0,T],V(t)is relatively compact inXα.

Next we prove that the family of functionsis equi-continuous on interval(0,T].Land then

whereε＞0 is sufficiently small.Sinceis strongly continuous,and the compactness ofS(t),t＞0 implies the continuity in the uniform operator topology,it follows thattends to zero asand henceis equicontinuous.Accordingly,from Theorem 2.2,is a completely continuous operator on

These arguments enable us to infer thatis a condense mapping onB(r),and by Theorem 2.3,we conclude that there exists a fixed pointLetand thenis a fixed point of the operatorwhich implies that equation(1.1)admits a mild solutionson(−∞,T].The proof is completed.

Theorem 3.2Assume that the assumptions of Theorem3.1are satisfied with functions F(·,·)and G(·,·)uniformly bounded,and additionally suppose that the hypothesisholds.Then(1.1)is approximately controllable on[0,T].

Proof Letxλ(·)be a fixed point ofQλonB(r),and then,as one can see above,is a mild solution to(1.1)on(−∞,T]under the control

Thus by(3.8)we have that

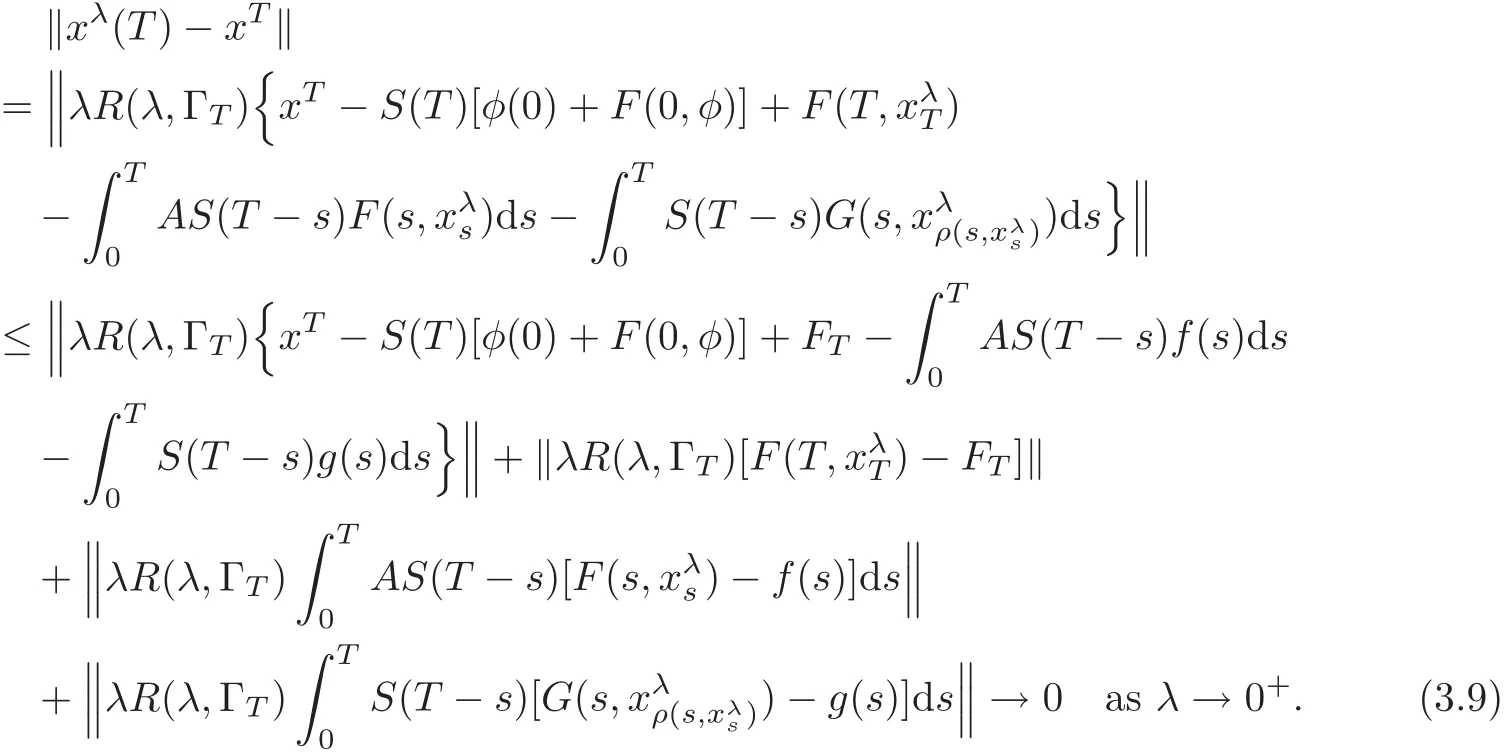
So there holdsinX,and consequently we obtain the approximate controllability of(1.1).The proof is completed.

4 An Example

In order to apply Theorem 3.1 and Theorem 3.2,we consider the following system:

and the norm is defined by,for

Then the system(4.1)is rewritten in the abstract form(1.1),and condition(i)implies thatR(F)⊂D(A),since

Thus,the condition(i)ensures thatAF(·)satisfies the Lipschitz continuous onIn fact,one has

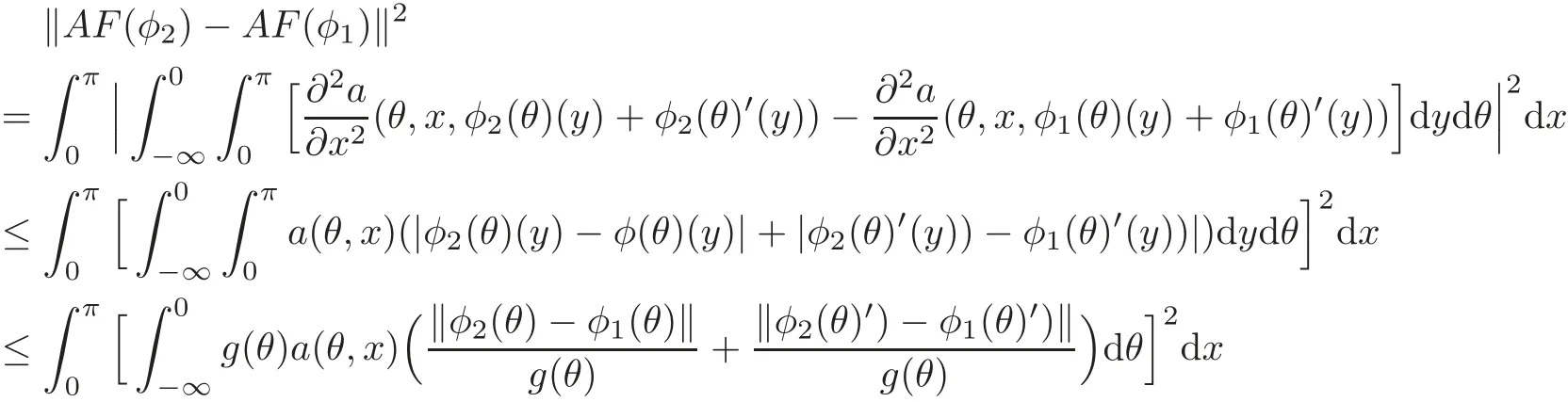
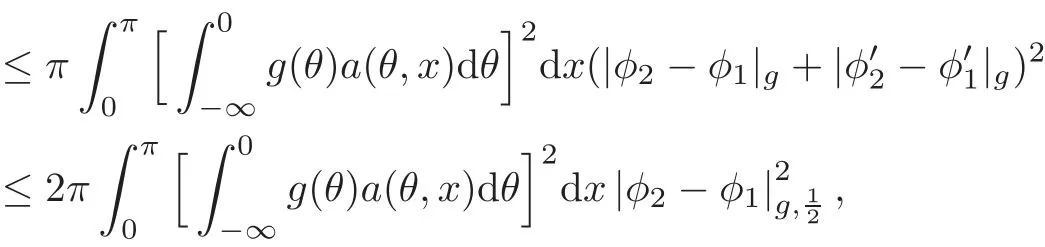
which shows the claim.Observing thatFandGalso verify(3.2)and(3.3)due to the assumptions(i)and(ii),we see that hypotheses(H2)and(H3)are satisfied respectively.Consequently,Theorem 3.2 is now well applied and the system(4.1)is approximate controllable on[0,T]provided that(3.6)is satisfied.

AcknowledgementThe authors are very grateful to the referees for their important comments and suggestions on this paper.

[1]Arino,O.,Habid,M.and de la Parra,R.,A mathematical model of growth of population of fish in the larval stage:Density-dependence effects,Math.Biosc.,150,1998,1–20.

[2]Bashirov,A.E.and Mahmudov,N.I.,On concepts of controllability for linear deterministic and stochastic systems,SIAM J.Control Optim.,37,1999,1808–1821.

[3]Balasubramaniam,P.and Ntouyas,S.K.,Controllability for neutral stochastic functional differential inclusions with in finite delay in abstract space,J.Math.Anal.Appl.,324,2006,161–176.

[4]Curtain,R.and Zwart,H.J.,An Introduction to In finite Dimensional Linear Systems Theory,Springer-Verlag,New York,1995.

[5]Dauer,J.P.and Mahmudov,N.I.,Approximate controllability of semilinear functional equations in Hilbert spaces,J.Math.Anal.Appl.,273,2002,310–327.

[6]Do,V.N.,A note on approximate controllability of semilinear systems,Syst.Contr.Lett.,12,1989,365–371.

[7]Ezzinbi,K.,Fu,X.and Hilal,K.,Existence and regularity in theα-norm for some neutral partial differential equations with nonlocal conditions,Nonl.Anal.,67,2007,1613–1622.

[8]Fu,X.and Mei,K.,Approximate controllability of semilinear partial functional differential systems,J.Dyn.Contr.Syst.,15,2009,425–443.

[9]Guendouzi,T.and Bousmaha,L.,Approximate controllability of fractional neutral stochastic functional integro-differential inclusions with in finite delay,Qual.Theory Dyn.Syst.,13,2014,89–119.

[10]Hale,J.and Kato,J.,Phase space for retarded equations with in finite delay,Funk.ekvac.,21,1978,11–41.

[11]Hale,J.and Verduyn-Lunel,S.,Introduction to Functional Differential Equations,Springer-Verlag,New York,1993.

[12]Hern´andez,E.and Henr´iquez,H.R.,Existence results for partial neutral functional differential equations with unbounded delay,J.Math.Anal.Appl.,221,1998,452–475.

[13]Hino,Y.,Murakami,S.and Naito,T.,Functional differential equations with in finite delay,Lecture Notes in Math.,Springer-Verlag,Berlin,1991.

[14]Jeong,J.,Kwun,Y.and Park,J.,Approximate controllability for semilinear retarded functional differential equations,J.Dyn.Contr.Syst.,5,1999,329–346.

[15]Joshi,M.C.and Sukavanam,N.,Approximate solvability of semilinear operator equations,Nonlinearity,3,1990,519–525.

[16]Li,X.and Yong,J.,Optimal Control Theory for In finite Dimensional Systems,Birkhanser,Berlin,1995.

[17]Mahaffy,J.,Belair,J.and Mackey,M.,Hematopoietic model with moving boundary condition and state dependent delay:Applications in Erythropoiesis,J.Theo.Biol.,190,1998,135–146.

[18]Mahmudov,N.I.and Zorlu,S.,On the approximate controllability of fractional evolution equations with compact analytic semigroup,J.Comput.Appl.Math.Ser.A,259,2014,194–204.

[19]Muthukumar,P.and Rajivganthi,C.,Approximate controllability of stochastic nonlinear third-order dispersion equation,Internat.J.Robust Nonl.Control,24,2014,585–594.

[20]Naito,K.,Controllability of semilinear control systems dominated by the linear part,SIAM J.Control Optim.,25,1987,715–722.

[21]Naito,K.,Approximate controllability for trajectories of semilinear control systems,J.Optim.Theory Appl.,60,1989,57–65.

[22]Pazy,A.,Semigroups of Linear Operators and Applications to Partial Differential Equations,Springer-Verlag,New York,1983.

[23]Sadovskii,B.N.,On a fixed point principle,Funct.Anal.Appl.,1,1967,74–76.

[24]Sakthivel,R.and Ananndhi,E.R.,Approximate controllability of impulsive differential equations with state-dependent delay,Inter.J.Control.,83,2010,387–393.

[25]Sakthivel,R.,Mahmudov,N.I.and Kim,J.H.,Approximate controllability of nonlinear impulsive differential systems,Reports Math.Phys.,60,2007,85–96.

[26]Sakthivel,R.and Ren,Y.,Approximate controllability of fractional differential equations with statedependent delay,Results Math.,63,2013,949–963.

[27]Sakthivel,R.,Ren,Y.and Mahmudov,N.I.,On the approximate controllability of semilinear fractional differential systems,Comp.Math.Appl.,62,2011,1451–1459.

[28]Travis,C.C.and Webb,G.F.,Partial differential equations with deviating arguments in the time variable,J.Math.Anal.Appl.,56,1976,397–409.

[29]Travis,C.C.and Webb,G.F.,Existence,stability and compactness in theα-norm for partial functional differential equations,Trans.Amer.Math.Soc.,240,1978,129–143.

[30]Naito,K.,Approximate controllability for integrodifferential equationswith multiple delays,J.Optim.Theory Appl.,143,2009,185–206.

[31]Wu,J.,Theory and Applications of Partial Functional Differential Equations,Springer-Verlag,Berlin,1996.

[32]Yamamoto,M.and Park,J.Y.,Controllability for parabolic equations with uniformly bounded nonlinear terms,J.Optim.Theory Appl.,66,1990,515–532.

[33]Yan,Z.,Approximate controllability of partial neutral functional differential systems of fractional order with state-dependent delay,Int.J.Contr.,85,2012,1051–1062.

[34]Yan,Z.,Approximate controllability of fractional neutral integro-differential inclusions with statedependent delay in Hilbert spaces,IMA J.Math.Control Inform.,30,2013,443–462.

[35]Zhou,H.X.,Approximate controllability for a class of semilinear abstract equations,SIAM J.Control Optim.,21,1983,551–565.