多工况下互连式油气悬架系统建模及特性研究
张军伟+杨波+李洪彪+陈思忠+李辰


摘 要:采用模块化的建模方法,建立系统中各个部件的模型,通过对各部件数学模型的原理分析,确定各部件模型的输入和输出。根据油气悬架系统的连接关系将各个部件模型连接起来,得到多工况下的互连式油气悬架系统数学模型。基于所建立的互连式油气悬架模型,对多种典型工况下的系统特性进行分析,得到互连式油气悬架主要参数的变化特性,为互连式油气悬架整车控制算法研究提供理论基础。
关键词:互连式;油气悬架;多工况;模块化建模;系统特性
中图分类号:U463.33 文献标文献标识码:A文献标DOI:10.3969/j.issn.2095-1469.2016.03.09
Abstract:The system model was built up and the characteristics of the interconnected hydropneumatic suspension were studied under multiple modes. The paper provides a theoretical foundation for the research on the whole vehicle control algorithm.
Keywords:interconnected; hydropneumatic suspension; multiple mode; modularity modeling; system characteristics
由于互连式油气悬架在平衡轴荷、刚度非线性、阻尼可调、抗侧倾等方面有着显著的优势,所以被越来越多地应用在多轴重型车辆上[1-5]。
多油缸互连式油气悬架的各油缸上、下腔之间对应或交叉连通,每个油缸与多条油路连通,每条油路中都装有阻尼阀和蓄能器。阻尼阀的非线性、蓄能器内气体状态变化的非线性、各油路之间交叉连通的非线性,致使互连式油气悬架成为一个非常复杂的系统[6-9]。由于互连式油气悬架结构的复杂性,很难利用台架试验对其系统动态特性进行研究,因此,很有必要对互连式油气悬架进行建模,对各种工况下的系统动态特性进行分析。
国内外相关领域的学者从多方面应用各种方法对油气悬架进行了深入的研究,但所研究对象多为结构简单的单回路油气悬架,且多为公式推导式的黑匣子建模方法,不便于中间结果的输出,也不易对整个油气悬架系统模型有一个透彻的认识。
采用传统的公式推导式建模方法已很难建立互连式油气悬架模型。针对结构复杂的互连式油气悬架,本文采用模块化建模方法,首先建立油气悬架系统中各个部件的模型,然后通过对各部件模型的原理分析,确定各部件模型之间的输入和输出关系,最后根据油气悬架系统的连接关系将各个部件模型连接起来,得到多工况下的互连式油气悬架系统数学模型。模块化的建模方法,便于中间结果的输出,例如某个阀的流量、蓄能器任意时刻的压力等,整体结构非常清晰,能够对系统模型各部分之间的关系有一个透彻的认识,能够将复杂的系统分割成一个个简单部件,适用于复杂系统的建模。
1 互连式油气悬架结构
某种用于四轴重型车辆的互连式油气悬架,前两桥连通结构与后两桥相同,一二桥的结构如图1所示。系统油缸为双腔油缸,上腔为环形腔,下腔为无杆腔;前后桥同侧油缸上、下腔对应连通,同桥左、右侧油缸上、下腔交叉连通。压缩行程时,油缸下腔的油液经多条支路流向蓄能器,压缩蓄能器内的气体产生弹性力,油液流过油路中的阻尼阀产生阻尼力。
为了实现多轴车辆的轴荷平衡及抗侧倾功能,油气悬架的各油缸之间是按照一定的规则连通的,这就不可避免地存在单个油缸连通多条支路的结构。在不影响系统特性的前提下,省略系统中的部分电磁阀,对系统进行简化处理,简化后的系统原理如图2所示。
由图2可知,互连式油气悬架的油缸为双腔油缸,同侧前后桥油缸上、下腔对应连通,实现平衡轴荷功能,同桥左、右侧油缸上、下腔交叉连通,实现抗侧倾功能。通过系统中的电磁阀控制,可以实现悬架刚度控制、侧倾刚度控制、阻尼连续控制、车高控制、单轮隔离、单轮提升、刚性闭锁等功能。
2 互连式油气悬架模型
互连式油气悬架系统中存在多条支路,每条支路中有多个阀,系统中有多个蓄能器,阻尼力的非线性和弹性力的非线性造成互连式油气悬架系统是一个非常复杂的非线性耦合系统,很难推导出显式格式的弹性力、阻尼力、输出力、系统压力等的表达式。因此,通过模块化的建模方法,得到整个油气悬架系统的数学模型。
2.1 油缸无杆腔连通油路模型
复杂的连通关系导致了单个油缸与多条支路连通,以油缸1R为例,若油缸1R作为作动缸,其它三个油缸为负载缸,定义无杆腔受压缩时位移为正,无杆腔伸张时位移为负,则油缸1R无杆腔的油路连通关系及油液流动线路如图3所示。分析可知,油缸1R无杆腔流出的油液有六个去处,分别为蓄能器A1R、蓄能器A2R、油缸2R无杆腔、蓄能器AfR、油缸1L有杆腔、油缸2L有杆腔。
建立油缸1R无杆腔压力微分方程,如式(1)所示。
式中:p1R-p为油缸1R无杆腔的压力,Pa;x1R、分别为油缸1R活塞位移和速度,m/s;Ap为油缸无杆腔横截面积,m2;dp为油缸无杆腔直径,m;dr是油缸有杆腔直径,m;Q2R-p为油缸2R无杆腔流量,m3/s;QA1R为蓄能器A1R支路的流量,m3/s;QA2R为蓄能器A2R支路的流量,m3/s;QAfR为蓄能器AfR支路的流量,m3/s;QL为左侧油缸1L、2L有杆腔油路中阀组的流量,m3/s;C1R-p为油缸1R无杆腔油路的容积模量,m3/Pa;Vb-p为静平衡位置的油缸无杆腔容积,m3;Koil为油液体积模量,Pa。
其中,各个部分的流量可根据阀和蓄能器的传统建模方法得到,这里不再详述,只将各支路流量表示为压差的函数形式[10-12],如式(2)所示。
式中:为油缸2R活塞速度,m/s;pA1R、pA2R、pAfR分别为蓄能器A1R、A2R、AfR内气体的压力,Pa;p12L-r为油缸1L、2L有杆腔压力,Pa。
2.2 油缸有杆腔连通油路模型
若油缸1R无杆腔受压缩,则有杆腔为伸张,油液从别处流入油缸1R有杆腔,油缸1R有杆腔的油路连通关系及油液流动线路如图4所示。
分析可知,流入油缸1R有杆腔的油液有六个来源,分别为油缸2R有杆腔、蓄能器AfL、蓄能器A1L、蓄能器A2L、油缸1L无杆腔、油缸2L无杆腔。建立油缸1R有杆腔压力微分方程[13],如式(3)所示。
式中:p1R-r为油缸1R有杆腔的压力,Pa;Q2R-r为油缸2R有杆腔流量,m3/s;QA1L为蓄能器A1L支路的流量,m3/s;QA2L为蓄能器A2L支路的流量,m3/s;QAfL为蓄能器AfL支路的流量,m3/s;QR为油缸1R、2R有杆腔连通油路中阀组的流量,m3/s;C1R-r为油缸1R有杆腔油路的容积模量,m3/Pa;Vb-r为静平衡位置的油缸有杆腔容积,m3。
其中,各个部分的流量同样可根据阀和蓄能器的传统建模得到,这里只将各支路流量表示为压差的函数形式,如式(4)所示。
式中:pA1L、pA2L、pAfL分别为蓄能器A1L、A2L、AfL内气体的压力,Pa;p12L-P为油缸1L、2L无杆腔压力,Pa。
2.3 互连式油气悬架模型
由式(1)~(4)可知,未知的参数包括油缸2R、1L、2L活塞的速度、、,利用牛顿定律,分别对三个油缸活塞列出受力平衡方程来求得三个活塞的速度。油缸活塞受力分析如图5所示。油缸活塞共受五个作用力,分别为油缸无杆腔压力 ppAp,油缸有杆腔压力prAr,簧载质量作用于活塞杆的重力msg,活塞杆自身的重力mpg,活塞与油缸之间的摩擦力Ff。油缸2R、1L、2L活塞动力学方程如式(5)所示。
由式(5)可知,需求出油缸2R无杆腔压力p2R-p和有杆腔压力p2R-r,油缸1L无杆腔压力p1L-p和有杆腔压力p1L-r,油缸2L无杆腔压力p2L-p和有杆腔压力p2L-r。
由于油缸2R与1R直接连通,油路中不含任何阀,若忽略管路的压力损失,则油缸2R的两个腔与油缸1R的两个腔具有相同的压力,如式(6)所示。
油缸1L和2L也是直接连通,那么油缸1L的两个腔与油缸2L的两个腔具有相同的压力。首先求油缸1L、2L有杆腔压力(图3),根据油缸1L、2L有杆腔连通油路中的阀组压差/流量关系,又因油缸1L、2L负载和结构参数相同,则油缸1L和2L的流量相同,即可得到油缸1L、2L有杆腔压力与活塞速度关系式(7)。
如图4所示,同理可求得油缸1L、2L无杆腔压力与活塞速度关系式(8)。
其中,活塞和油缸之间的摩擦力采用基于Stribeck曲线拟合的公式来计算,如式(9)所示。
式中:fv表示粘性摩擦系数;fc表示库仑摩擦力,N; fs表示静摩擦力,N;τs表示静摩擦力因数;表示活塞运动速度,m/s。
联立式(1)~(9),结合传统建模方法得到的各种阀和蓄能器的模型,将各式具体化,进而在Matlab/Simulink中实现单轮激励工况下的互连式油气悬架数学模型[14],模型流程图如图6所示。
2.4 油气悬架部件模型验证
为了验证所建立的油气悬架主要阀、蓄能器、弹性力和阻尼力数学模型的正确性,进行了台架试验。试验设备采用车辆悬架测试系统(FCS佛力系统),将油缸竖直安装在测试系统上,如图7所示。
试验条件见表1。
所载入的载荷谱见表2。
在0.01 Hz/0.03 m载荷谱激励情况下,由于油缸活塞运动速度非常小,油液流过阻尼阀产生的阻尼力几乎为0,因此,可以近似认为此时活塞杆的输出力即为弹性力。
图8a是原始数据及拟合曲线,黑色波动的上下两条曲线为原始试验曲线,可以近似认为压缩和伸张行程中的摩擦力大小相等,方向相反,两条曲线的差值即为活塞与油缸之间摩擦力的两倍,去除摩擦力之后再拟合的曲线如图8a中的红色曲线。图8b中,黑色是仿真的弹性力曲线,红色是弹性力试验拟合曲线,由图可知,仿真曲线与试验曲线吻合较好,分析引起细微差别的可能原因,是由于试验部件中某些参数的不确定性以及橡胶油管的弹性变形。
在0.5 Hz/0.03 m和1.0 Hz/0.03 m载荷谱激励情况下,活塞杆输出力包括摩擦力、弹性力、阻尼力,活塞杆输出力去除摩擦力和弹性力,得到阻尼力。仿真曲线与试验曲线对比如图9所示。
图9a和b分别是激励0.5 Hz/0.03 m下的阻尼力-位移曲线对比和阻尼力-速度曲线对比,可以看出,仿真曲线与试验曲线吻合较好,表明仿真的结果比较接近实际情况。
上述仿真与试验对比表明,所建立的油气悬架各部件模型是正确的,基于此模型所建立的互连式油气悬架模型以及后续的系统特性分析是可信的。
3 各工况下的系统动态特性
3.1 单轮激励工况系统动态特性
车辆在行驶过程中,各车轮受到的路面激励是随机的。针对互连式油气悬架,以单个油缸作为作动缸,其它油缸作为随动缸,以此来模拟车辆行驶过程中单轮激励工况,进行系统动态特性研究。
以油缸1R为作动缸,给油缸1R加入2.0 Hz/
30 mm的半正弦激励信号,如图10所示,模拟车辆以1 m/s的车速驶过一个高30 mm、跨度250 mm的减速带。
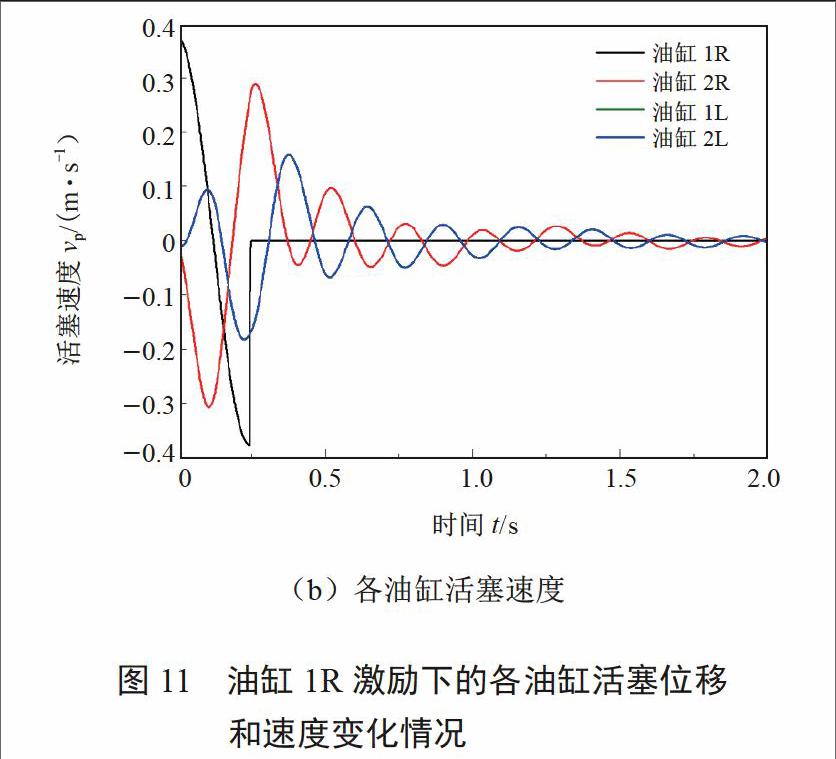
由图11a可知,油缸2R的位移与油缸1R相反,且油缸2R受到油路长度等因素的影响,在相位上有一定的延迟。油缸1L与油缸2L的运动情况相同,位移曲线重合,且由于右侧阀块与左侧阀块之间的油路较长且有很多阻尼阀,因此左侧油缸受影响较小,产生的位移也较小。2 s左右,各油缸趋于稳定,各油缸活塞位移变为0。
由图11b可以得到相同的结论,油缸2R活塞产生相反方向的速度,且受影响较大;油缸1L、2L产生相同方向的速度,且受影响较小。由于油路和阻尼阀的影响,油缸2R、1L、2L活塞速度在相位上都有一定的延迟。
由图12a可知,蓄能器A1R、A2R内气体压力变化基本相同,蓄能器AfR内的气体压力要比蓄能器A1R、A2R低一些;伸张行程则相反,油液从蓄能器A1R、A2R、AfR流入油缸1R无杆腔,蓄能器内气体压力降低。
由图12b可知,由于油缸1R、2R的有杆腔、无杆腔对应连通的结构,油缸1R、2R活塞杆输出力曲线基本重合。由于右侧油缸与左侧油缸有杆腔、无杆腔的交叉连通结构,油缸1L、2L活塞杆输出力与油缸1R、2R活塞杆输出力相位相反。油缸1R、2R都是随动缸,且连通结构完全相同,因此,油缸1R、2R的活塞杆输出力情况是相同的。
3.2 同侧前后轮激励工况系统动态特性
针对互连式油气悬架,采用同一侧前后桥油缸同时受到激励的方式来模拟车辆行驶过程中同侧前后桥车轮同时受路面激励工况,进行系统动态特性研究。
同理得到同侧前后轮激励工况下的数学模型,同侧前后轮激励工况下的互连式油气悬架模型流程图与图6类似,只需将系统输入替换为油缸1R、2R。
针对同侧前后轮反相位激励工况,以油缸1R、2R为作动缸,油缸1L、2L为随动缸,给油缸1R、2R加入反相位2.0 Hz/30 mm的半正弦激励信号,如图13所示。
由图14a可知,油缸2R活塞位移相位与1R相反,油缸1L、2L活塞位移非常小,几乎不受右侧油缸的影响。图14b为同侧前后油缸1R、2R反相位激励下的各油缸活塞速度变化情况,由速度图同样可以看出,油缸1L、2L活塞的速度非常小,受右侧油缸的影响非常小。
由图15a可知,由于油缸1R与2R有杆腔、无杆腔的对应连通关系,以及反相位的激励,右侧的三个蓄能器内气体压力变化很小,只有0.1 MPa的上下波动量。同样,左侧的三个蓄能器内气体压力变化也很小。由图15a还可知,右侧蓄能器内气体的稳定压力要稍高于左侧蓄能器的稳定压力。
由图15b可知,由于油缸1R与2R有杆腔、无杆腔的对应连通关系,以及反相位的激励,绝大部分的油液只在油缸1R、2R的有杆腔、无杆腔之间自由流动,因此,各油缸活塞杆的输出力波动很小。
3.3 同桥左右轮激励工况模型及系统动态特性
车辆在行驶过程中,会遇到左右车轮同时轧到凸台或凹坑的情况,针对互连式油气悬架,采用同一桥的左右两个油缸同时受到激励的方式来模拟车辆行驶过程中同一桥左右轮同时受到路面激励的工况,进行系统动态特性研究。
同理得到同桥左右轮激励工况下的数学模型,同桥左右轮激励工况下的互连式油气悬架模型流程图与图6类似,只需将系统输入替换为1R、1L。
针对同桥左右轮同相位激励工况,以油缸1R、1L为作动缸,油缸2R、2L为随动缸,给油缸1R、1L加入同相位2.0 Hz/30 mm的半正弦激励信号,如图16所示。
由图17a可知,油缸2R、2L活塞位移变化情况相同,都呈反相位。由于油路及阻尼阀的影响,油缸2R、2L的位移在相位上有一定的延迟,经过4 s,位移变为0,系统趋于稳定。由图17b可知,油缸2R、2L活塞速度变化情况相同,呈反相位,经过4 s之后系统趋于稳定。
图18a可知,油缸1R、1L对各自一侧的蓄能器的影响是相同的,因此,蓄能器A1R、A2R、A1L、A2L内气体压力的变化规律是相同的,蓄能器AfR与AfL内气体压力的变化规律是相同的,但在幅值上小于另外四个边侧蓄能器。由图18b可知,四个油缸的活塞杆输出力变化情况是相同的,这是由于同侧油缸有杆腔、无杆腔对应连通,右侧与左侧油缸有杆腔、无杆腔交叉连通,且系统是在油缸1R、1L同相位激励下,造成了各油缸活塞杆的输出力变化规律是相同的。
4 结论
(1)针对互连式油气悬架系统结构复杂的特点,在建立各阀、蓄能器和油缸等部件模型的基础上,采用模块化建模的方法,根据系统中各部件的连通关系,分析互连式油气悬架系统中各部件模型之间的输入输出关系,建立了互连式油气悬架模型。
(2)基于建立的互连式油气悬架模型,对互连式油气悬架油缸活塞位移、油缸活塞速度、油缸输出力、蓄能器内的气体压力变化进行分析,得到各工况下的互连式油气悬架系统动态特性。
(3)分析结果表明:在单轮激励工况下,与作动油缸同侧的随动油缸及蓄能器产生同向的动态变化,与作动油缸异侧的随动油缸及蓄能器产生反向的动态变化,且同侧的随动油缸受影响较大,异侧的随动油缸受影响较小。
(4)在同侧前后轮反相位激励工况下,与作动油缸异侧的随动油缸受影响很小,系统中各蓄能器内气体压力及各油缸输出力变化也很小,系统动态特性比较平和。
(5)在同桥左右轮同相位激励工况下,系统中各蓄能器内气体压力及各油缸输出力变化规律都相同,即系统对称部件的动态特性完全相同。
由于互连式油气悬架在平衡轴荷、刚度非线性、阻尼可调、抗侧倾等方面有着显著的优势,所以被越来越多地应用在多轴重型车辆上[1-5]。
多油缸互连式油气悬架的各油缸上、下腔之间对应或交叉连通,每个油缸与多条油路连通,每条油路中都装有阻尼阀和蓄能器。阻尼阀的非线性、蓄能器内气体状态变化的非线性、各油路之间交叉连通的非线性,致使互连式油气悬架成为一个非常复杂的系统[6-9]。由于互连式油气悬架结构的复杂性,很难利用台架试验对其系统动态特性进行研究,因此,很有必要对互连式油气悬架进行建模,对各种工况下的系统动态特性进行分析。
国内外相关领域的学者从多方面应用各种方法对油气悬架进行了深入的研究,但所研究对象多为结构简单的单回路油气悬架,且多为公式推导式的黑匣子建模方法,不便于中间结果的输出,也不易对整个油气悬架系统模型有一个透彻的认识。
采用传统的公式推导式建模方法已很难建立互连式油气悬架模型。针对结构复杂的互连式油气悬架,本文采用模块化建模方法,首先建立油气悬架系统中各个部件的模型,然后通过对各部件模型的原理分析,确定各部件模型之间的输入和输出关系,最后根据油气悬架系统的连接关系将各个部件模型连接起来,得到多工况下的互连式油气悬架系统数学模型。模块化的建模方法,便于中间结果的输出,例如某个阀的流量、蓄能器任意时刻的压力等,整体结构非常清晰,能够对系统模型各部分之间的关系有一个透彻的认识,能够将复杂的系统分割成一个个简单部件,适用于复杂系统的建模。
1 互连式油气悬架结构
某种用于四轴重型车辆的互连式油气悬架,前两桥连通结构与后两桥相同,一二桥的结构如图1所示。系统油缸为双腔油缸,上腔为环形腔,下腔为无杆腔;前后桥同侧油缸上、下腔对应连通,同桥左、右侧油缸上、下腔交叉连通。压缩行程时,油缸下腔的油液经多条支路流向蓄能器,压缩蓄能器内的气体产生弹性力,油液流过油路中的阻尼阀产生阻尼力。
为了实现多轴车辆的轴荷平衡及抗侧倾功能,油气悬架的各油缸之间是按照一定的规则连通的,这就不可避免地存在单个油缸连通多条支路的结构。在不影响系统特性的前提下,省略系统中的部分电磁阀,对系统进行简化处理,简化后的系统原理如图2所示。
由图2可知,互连式油气悬架的油缸为双腔油缸,同侧前后桥油缸上、下腔对应连通,实现平衡轴荷功能,同桥左、右侧油缸上、下腔交叉连通,实现抗侧倾功能。通过系统中的电磁阀控制,可以实现悬架刚度控制、侧倾刚度控制、阻尼连续控制、车高控制、单轮隔离、单轮提升、刚性闭锁等功能。
2 互连式油气悬架模型
互连式油气悬架系统中存在多条支路,每条支路中有多个阀,系统中有多个蓄能器,阻尼力的非线性和弹性力的非线性造成互连式油气悬架系统是一个非常复杂的非线性耦合系统,很难推导出显式格式的弹性力、阻尼力、输出力、系统压力等的表达式。因此,通过模块化的建模方法,得到整个油气悬架系统的数学模型。
2.1 油缸无杆腔连通油路模型
复杂的连通关系导致了单个油缸与多条支路连通,以油缸1R为例,若油缸1R作为作动缸,其它三个油缸为负载缸,定义无杆腔受压缩时位移为正,无杆腔伸张时位移为负,则油缸1R无杆腔的油路连通关系及油液流动线路如图3所示。分析可知,油缸1R无杆腔流出的油液有六个去处,分别为蓄能器A1R、蓄能器A2R、油缸2R无杆腔、蓄能器AfR、油缸1L有杆腔、油缸2L有杆腔。
建立油缸1R无杆腔压力微分方程,如式(1)所示。
式中:p1R-p为油缸1R无杆腔的压力,Pa;x1R、分别为油缸1R活塞位移和速度,m/s;Ap为油缸无杆腔横截面积,m2;dp为油缸无杆腔直径,m;dr是油缸有杆腔直径,m;Q2R-p为油缸2R无杆腔流量,m3/s;QA1R为蓄能器A1R支路的流量,m3/s;QA2R为蓄能器A2R支路的流量,m3/s;QAfR为蓄能器AfR支路的流量,m3/s;QL为左侧油缸1L、2L有杆腔油路中阀组的流量,m3/s;C1R-p为油缸1R无杆腔油路的容积模量,m3/Pa;Vb-p为静平衡位置的油缸无杆腔容积,m3;Koil为油液体积模量,Pa。
其中,各个部分的流量可根据阀和蓄能器的传统建模方法得到,这里不再详述,只将各支路流量表示为压差的函数形式[10-12],如式(2)所示。
式中:为油缸2R活塞速度,m/s;pA1R、pA2R、pAfR分别为蓄能器A1R、A2R、AfR内气体的压力,Pa;p12L-r为油缸1L、2L有杆腔压力,Pa。
2.2 油缸有杆腔连通油路模型
若油缸1R无杆腔受压缩,则有杆腔为伸张,油液从别处流入油缸1R有杆腔,油缸1R有杆腔的油路连通关系及油液流动线路如图4所示。
分析可知,流入油缸1R有杆腔的油液有六个来源,分别为油缸2R有杆腔、蓄能器AfL、蓄能器A1L、蓄能器A2L、油缸1L无杆腔、油缸2L无杆腔。建立油缸1R有杆腔压力微分方程[13],如式(3)所示。
式中:p1R-r为油缸1R有杆腔的压力,Pa;Q2R-r为油缸2R有杆腔流量,m3/s;QA1L为蓄能器A1L支路的流量,m3/s;QA2L为蓄能器A2L支路的流量,m3/s;QAfL为蓄能器AfL支路的流量,m3/s;QR为油缸1R、2R有杆腔连通油路中阀组的流量,m3/s;C1R-r为油缸1R有杆腔油路的容积模量,m3/Pa;Vb-r为静平衡位置的油缸有杆腔容积,m3。
其中,各个部分的流量同样可根据阀和蓄能器的传统建模得到,这里只将各支路流量表示为压差的函数形式,如式(4)所示。
式中:pA1L、pA2L、pAfL分别为蓄能器A1L、A2L、AfL内气体的压力,Pa;p12L-P为油缸1L、2L无杆腔压力,Pa。
2.3 互连式油气悬架模型
由式(1)~(4)可知,未知的参数包括油缸2R、1L、2L活塞的速度、、,利用牛顿定律,分别对三个油缸活塞列出受力平衡方程来求得三个活塞的速度。油缸活塞受力分析如图5所示。油缸活塞共受五个作用力,分别为油缸无杆腔压力 ppAp,油缸有杆腔压力prAr,簧载质量作用于活塞杆的重力msg,活塞杆自身的重力mpg,活塞与油缸之间的摩擦力Ff。油缸2R、1L、2L活塞动力学方程如式(5)所示。
由式(5)可知,需求出油缸2R无杆腔压力p2R-p和有杆腔压力p2R-r,油缸1L无杆腔压力p1L-p和有杆腔压力p1L-r,油缸2L无杆腔压力p2L-p和有杆腔压力p2L-r。
由于油缸2R与1R直接连通,油路中不含任何阀,若忽略管路的压力损失,则油缸2R的两个腔与油缸1R的两个腔具有相同的压力,如式(6)所示。
油缸1L和2L也是直接连通,那么油缸1L的两个腔与油缸2L的两个腔具有相同的压力。首先求油缸1L、2L有杆腔压力(图3),根据油缸1L、2L有杆腔连通油路中的阀组压差/流量关系,又因油缸1L、2L负载和结构参数相同,则油缸1L和2L的流量相同,即可得到油缸1L、2L有杆腔压力与活塞速度关系式(7)。
如图4所示,同理可求得油缸1L、2L无杆腔压力与活塞速度关系式(8)。
其中,活塞和油缸之间的摩擦力采用基于Stribeck曲线拟合的公式来计算,如式(9)所示。
式中:fv表示粘性摩擦系数;fc表示库仑摩擦力,N; fs表示静摩擦力,N;τs表示静摩擦力因数;表示活塞运动速度,m/s。
联立式(1)~(9),结合传统建模方法得到的各种阀和蓄能器的模型,将各式具体化,进而在Matlab/Simulink中实现单轮激励工况下的互连式油气悬架数学模型[14],模型流程图如图6所示。
2.4 油气悬架部件模型验证
为了验证所建立的油气悬架主要阀、蓄能器、弹性力和阻尼力数学模型的正确性,进行了台架试验。试验设备采用车辆悬架测试系统(FCS佛力系统),将油缸竖直安装在测试系统上,如图7所示。
试验条件见表1。
所载入的载荷谱见表2。
在0.01 Hz/0.03 m载荷谱激励情况下,由于油缸活塞运动速度非常小,油液流过阻尼阀产生的阻尼力几乎为0,因此,可以近似认为此时活塞杆的输出力即为弹性力。
图8a是原始数据及拟合曲线,黑色波动的上下两条曲线为原始试验曲线,可以近似认为压缩和伸张行程中的摩擦力大小相等,方向相反,两条曲线的差值即为活塞与油缸之间摩擦力的两倍,去除摩擦力之后再拟合的曲线如图8a中的红色曲线。图8b中,黑色是仿真的弹性力曲线,红色是弹性力试验拟合曲线,由图可知,仿真曲线与试验曲线吻合较好,分析引起细微差别的可能原因,是由于试验部件中某些参数的不确定性以及橡胶油管的弹性变形。
在0.5 Hz/0.03 m和1.0 Hz/0.03 m载荷谱激励情况下,活塞杆输出力包括摩擦力、弹性力、阻尼力,活塞杆输出力去除摩擦力和弹性力,得到阻尼力。仿真曲线与试验曲线对比如图9所示。
图9a和b分别是激励0.5 Hz/0.03 m下的阻尼力-位移曲线对比和阻尼力-速度曲线对比,可以看出,仿真曲线与试验曲线吻合较好,表明仿真的结果比较接近实际情况。
上述仿真与试验对比表明,所建立的油气悬架各部件模型是正确的,基于此模型所建立的互连式油气悬架模型以及后续的系统特性分析是可信的。
3 各工况下的系统动态特性
3.1 单轮激励工况系统动态特性
车辆在行驶过程中,各车轮受到的路面激励是随机的。针对互连式油气悬架,以单个油缸作为作动缸,其它油缸作为随动缸,以此来模拟车辆行驶过程中单轮激励工况,进行系统动态特性研究。
以油缸1R为作动缸,给油缸1R加入2.0 Hz/
30 mm的半正弦激励信号,如图10所示,模拟车辆以1 m/s的车速驶过一个高30 mm、跨度250 mm的减速带。
由图11a可知,油缸2R的位移与油缸1R相反,且油缸2R受到油路长度等因素的影响,在相位上有一定的延迟。油缸1L与油缸2L的运动情况相同,位移曲线重合,且由于右侧阀块与左侧阀块之间的油路较长且有很多阻尼阀,因此左侧油缸受影响较小,产生的位移也较小。2 s左右,各油缸趋于稳定,各油缸活塞位移变为0。
由图11b可以得到相同的结论,油缸2R活塞产生相反方向的速度,且受影响较大;油缸1L、2L产生相同方向的速度,且受影响较小。由于油路和阻尼阀的影响,油缸2R、1L、2L活塞速度在相位上都有一定的延迟。
由图12a可知,蓄能器A1R、A2R内气体压力变化基本相同,蓄能器AfR内的气体压力要比蓄能器A1R、A2R低一些;伸张行程则相反,油液从蓄能器A1R、A2R、AfR流入油缸1R无杆腔,蓄能器内气体压力降低。
由图12b可知,由于油缸1R、2R的有杆腔、无杆腔对应连通的结构,油缸1R、2R活塞杆输出力曲线基本重合。由于右侧油缸与左侧油缸有杆腔、无杆腔的交叉连通结构,油缸1L、2L活塞杆输出力与油缸1R、2R活塞杆输出力相位相反。油缸1R、2R都是随动缸,且连通结构完全相同,因此,油缸1R、2R的活塞杆输出力情况是相同的。
3.2 同侧前后轮激励工况系统动态特性
针对互连式油气悬架,采用同一侧前后桥油缸同时受到激励的方式来模拟车辆行驶过程中同侧前后桥车轮同时受路面激励工况,进行系统动态特性研究。
同理得到同侧前后轮激励工况下的数学模型,同侧前后轮激励工况下的互连式油气悬架模型流程图与图6类似,只需将系统输入替换为油缸1R、2R。
针对同侧前后轮反相位激励工况,以油缸1R、2R为作动缸,油缸1L、2L为随动缸,给油缸1R、2R加入反相位2.0 Hz/30 mm的半正弦激励信号,如图13所示。
由图14a可知,油缸2R活塞位移相位与1R相反,油缸1L、2L活塞位移非常小,几乎不受右侧油缸的影响。图14b为同侧前后油缸1R、2R反相位激励下的各油缸活塞速度变化情况,由速度图同样可以看出,油缸1L、2L活塞的速度非常小,受右侧油缸的影响非常小。
由图15a可知,由于油缸1R与2R有杆腔、无杆腔的对应连通关系,以及反相位的激励,右侧的三个蓄能器内气体压力变化很小,只有0.1 MPa的上下波动量。同样,左侧的三个蓄能器内气体压力变化也很小。由图15a还可知,右侧蓄能器内气体的稳定压力要稍高于左侧蓄能器的稳定压力。
由图15b可知,由于油缸1R与2R有杆腔、无杆腔的对应连通关系,以及反相位的激励,绝大部分的油液只在油缸1R、2R的有杆腔、无杆腔之间自由流动,因此,各油缸活塞杆的输出力波动很小。
3.3 同桥左右轮激励工况模型及系统动态特性
车辆在行驶过程中,会遇到左右车轮同时轧到凸台或凹坑的情况,针对互连式油气悬架,采用同一桥的左右两个油缸同时受到激励的方式来模拟车辆行驶过程中同一桥左右轮同时受到路面激励的工况,进行系统动态特性研究。
同理得到同桥左右轮激励工况下的数学模型,同桥左右轮激励工况下的互连式油气悬架模型流程图与图6类似,只需将系统输入替换为1R、1L。
针对同桥左右轮同相位激励工况,以油缸1R、1L为作动缸,油缸2R、2L为随动缸,给油缸1R、1L加入同相位2.0 Hz/30 mm的半正弦激励信号,如图16所示。
由图17a可知,油缸2R、2L活塞位移变化情况相同,都呈反相位。由于油路及阻尼阀的影响,油缸2R、2L的位移在相位上有一定的延迟,经过4 s,位移变为0,系统趋于稳定。由图17b可知,油缸2R、2L活塞速度变化情况相同,呈反相位,经过4 s之后系统趋于稳定。
图18a可知,油缸1R、1L对各自一侧的蓄能器的影响是相同的,因此,蓄能器A1R、A2R、A1L、A2L内气体压力的变化规律是相同的,蓄能器AfR与AfL内气体压力的变化规律是相同的,但在幅值上小于另外四个边侧蓄能器。由图18b可知,四个油缸的活塞杆输出力变化情况是相同的,这是由于同侧油缸有杆腔、无杆腔对应连通,右侧与左侧油缸有杆腔、无杆腔交叉连通,且系统是在油缸1R、1L同相位激励下,造成了各油缸活塞杆的输出力变化规律是相同的。
4 结论
(1)针对互连式油气悬架系统结构复杂的特点,在建立各阀、蓄能器和油缸等部件模型的基础上,采用模块化建模的方法,根据系统中各部件的连通关系,分析互连式油气悬架系统中各部件模型之间的输入输出关系,建立了互连式油气悬架模型。
(2)基于建立的互连式油气悬架模型,对互连式油气悬架油缸活塞位移、油缸活塞速度、油缸输出力、蓄能器内的气体压力变化进行分析,得到各工况下的互连式油气悬架系统动态特性。
(3)分析结果表明:在单轮激励工况下,与作动油缸同侧的随动油缸及蓄能器产生同向的动态变化,与作动油缸异侧的随动油缸及蓄能器产生反向的动态变化,且同侧的随动油缸受影响较大,异侧的随动油缸受影响较小。
(4)在同侧前后轮反相位激励工况下,与作动油缸异侧的随动油缸受影响很小,系统中各蓄能器内气体压力及各油缸输出力变化也很小,系统动态特性比较平和。
(5)在同桥左右轮同相位激励工况下,系统中各蓄能器内气体压力及各油缸输出力变化规律都相同,即系统对称部件的动态特性完全相同。
参考文献(References):
CAO D,RAKHEJA S,SU C Y. Roll Plane Analysis of Interconnected Hydro-Pneumatic Suspension Struts [C]// ASME 2005 International Mechanical Engineering Congress and Exposition,2005:133-142.
CAO D,RAKHEJA S,SU C. Property Analysis of an X-coupled Suspension for Sport Utility Vehicles [J]. SAE International Journal of Passenger Cars Mechanical System,2009,1(1):853-862.
CAO D,RAKHEJA S,SU C Y. A Generalized Model of a Class of interconnected Hydro-Pneumatic Suspensions and Analysis of Pitch Properties [C]//ASME 2006 Inter-
national Mechanical Engineering Congress and Expo-sition,2006(1):137-146.
杨杰. 基于油气悬架的阻尼可调技术研究 [D]. 北京:北京理工大学,2009.
YANG Jie. Research on Adjustable Damping Technology Based on Hydropneumatic Suspension [D]. Beijing: Beijing Institute of Technology,2009. (in Chinese)
CAO D. Theoretical Analyses of Roll and Pitch-Coupled Hydro-Pneumatic Strut Suspensions [D]. Montreal: Concordia University,2008.
JOO F R. Dynamic Analysis of a Hydropneumatic Suspen-sion System [D]. Montreal:Concordia University,1991.
FELEZ J,VERA C. Bond Graph Assisted Models for Hydro-Pneumatic Suspensions in Crane Vehicles [J]. Vehicle System Dynamics,1987,16(5-6):313-332.
YOUSEFI A,LOHMANN B. Order Reduction of Nonlinear Hydropneumatic Vehicle Suspension [C]//Proceedings of the 2006 IEEE International Conference on Control Applications,Munich,2006:1404-1408.
ZHANG Junwei,CHEN Sizhong,YANG Lin. Research on Nonlinear Stiffness Characteristics of Hydro-Pneumatic Spring [J]. Applied Mechanics and Material,2012, 128-129:421-425.
REYBROUCK K. A Non Linear Parametric Model of an Automotive Shock Absorber [C]// SAE Techincal Paper 940869,1994.
杨杰,陈思忠,吴志成. 油气悬架可控刚度阻尼设计与试验 [J]. 农业机械学报,2008,39(10):11-24.
YANG Jie,CHEN Sizhong,WU Zhicheng. Design and Testing on the Hydropneumatic Suspensions with Controllable Stiffness and Damping [J]. Transactions of the Chinese Society for Agricultural Machinery,2008, 39(10):11-24. (in Chinese)
张军伟,陈思忠,吴志成. 刚度和阻尼均可调的油气悬架设计与试验 [J]. 汽车工程学报,2013,3(2):106-112.
ZHANG Junwei,CHEN Sizhong,WU Zhicheng. Design and Test of a Hydropneumatic Suspension with Adjustable Stiffness and Damping [J]. Chinese Journal of Automotive Engineering,2013,3(2):106-112. (in Chinese)
ZHANG Junwei,CHEN Sizhong. Modeling and Study on Active Vibration Control of an Off-Road Vehicle [J]. Vehicle System Dynamics,2014,52(5):581-607.
张军伟. 多轴重型车辆互连式油气悬架系统特性研究 [D]. 北京:北京理工大学,2015.
ZHANG Junwei. Research on System Characteristics of Interconnected Hydropneumatic Suspension for Multi-axle Heavy Vehicle [D]. Beijing:Beijing Institute of Technology,2009.(in Chinese)

