初中阶段数学学困生成因及转化策略研究
金秋保


每一名“学困生”都渴望得到表扬,渴望获得肯定。因此教师在平时的生活和教学中一定要注意培养“学困生”的良好行为习惯,从“学困生”的角度去思考,挖掘他们的闪光点,及时给予鼓励,让“学困生”真正感受到教师的关注和关爱,使“学困生”对数学的学习产生的兴趣。在《勾股定理》的习题课中笔者设计了下列例题:
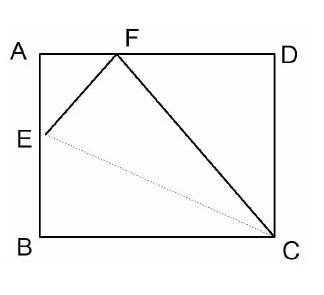
例:如图,已知矩形ABCD中,E是AB上一点,沿EC折叠,使点B落在AD边的F处,若AB=6,BC=10,求AE的长。
[解析]本题考察了矩形、对称、勾股定理等几何知识,综合性较强,有一定难度的试题。例题呈现后,好多学生从正面都无法下手,我并没用立刻抛出答案,而是给了学生充足的思考时间,让所有学生都参与进来,引导学生开始讨论,尤其关注“学困生”的参与情况。不久,就有一个学生到黑板上写出了自己的解答过程如:[解法1],利用方程思想,根据勾股定理中的等量关系得到方程;过了一段时间后又有两名学生用了两种不同的方法:[解法2] 根据面积不变性的等量关系得到方程;[解法3] 根据相似三角形的性质这个等量关系得到方程。
[方法指导]从分析问题的数量关系入手,适当设定未知数,把所研究的数学问题中已知量和未知量之间的数量关系,转化为方程或方程组的数学模型,从而使问题得到解决的思维方法——方程思想。巧用方程解几何题,在很多几何求解题中,当我们正面求解这条路不好走时,我们经常巧用方程思想解几何题。
[变式训练]
[解析]此题和例题有很多相似之处,都可以利用勾股定理中的等量关系得到方程,但是此题不能用面积不变性和相似三角形的性质得到方程,通过此类试题告诉学生学习要能够举一反三,触类旁通,但不可生搬硬套。最后引导学生归纳小结出————巧用方程解几何题的方法和步骤:
1.要善于用方程思想解决几何问题
2.几何图形中常用的等量关系是:①面积不变性;②勾股定理;③相似三角形的性质;④直角三角形的边与角的关系。
3.设好未知数后,要尽量把已知条件在图上标出来。
4.要尝试一题多解,选择最优方案。
通过教师的引导、分析和学生的讨论、探究,随后师生共同总结、归纳得出了巧用方程解几何题的一般方法。所以,在教学中,教师只要巧妙设计好例题,给学生营造快乐的课堂氛围,多关注学困生,让他们积极参与课堂讨论,就能有效激发他们的学习兴趣,提高他们的学习效率。(作者单位:江西省永丰县实验学校)

