“动作分层法”巧解中考概率题

◎刘伏文

“动作分层法”巧解中考概率题

◎刘伏文

概率为中考必考，一般都有大题，有时试题的游戏情景被设计得比较复杂，干扰因素多，考生难于理清思路，经常“因失误而丢分”。掌握“动作分层法”可迅速理清思路，并准确画出树状图来解决概率题。

中考；概率；解决方法

解决概率题时画树状图法的通用性更强，但很多学生难于掌握树状图的使用技巧，究其原因，主要在于如何“分层”。“分层”是画树状图的关键，传统的教学方法中没有一种直观的分层方法，一些比较理论化的教法让学生更加迷惑；在所有的概率题中，每个游戏都有“动作”。因此，“动作分层法”就是以游戏的“动作”作为分层的依据，一个动作为一层，有几个动作就分几层。下面以几个例题展开讨论。

例1.小明有四把不同的钥匙和两把不同的锁，其中有两把钥匙可以打开对应的这两把锁，另两把钥匙是不能打开这两把锁的。现随意取出一把钥匙去开其中一把锁。

(1)请用画树状图的方法表示所有可能的结果；

(2)求小明一次打开锁的概率。

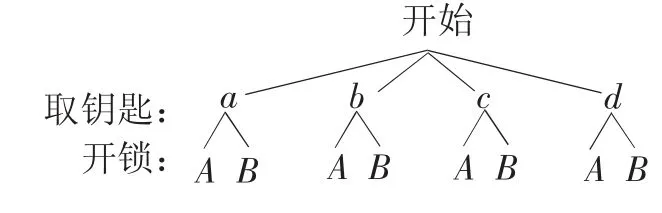
解析：本题较之一般的取物品游戏更有迷惑性，学生难于理清题目的层次。如果能抓住题中的“动作”，思路就很清晰。游戏关键是“随意取出一把钥匙去开其中一把锁”，其中包括“取钥匙”和“开锁”两个“动作”，因此，按先后顺序把“取钥匙”(有取a、b、c、d四把钥匙4种可能)作为树状图的第一层、“开锁”(有开A、B两把锁2种可能)作为树状图的第二层。

解：设四把不同的钥匙分别用a、b、c、d表示、两把不同的锁分别用A、B表示，且a、b钥匙能分别打开A、B锁，画树状图得：

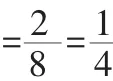
例2.如图，管中放置着三根同样的绳子AA1、BB1、CC1；

(1)小明从这三根绳子中随机选一根，恰好选中绳子AA1的概率是多少？

(2)小明先从左端A、B、C三个绳头中随机选两个打一个结，再从右端A1、B1、C1三个绳头中随机选两个打一个结，求这三根绳子能连结成一根长绳的概率。

解析：第(1)小题考查概率的基本概念，比较简单。第(2)小题中包含“从左端打结”和“从右端打结”两个“动作，因此，按先后顺序“从左端打结”(有A与B、B与C、A与C打结3种可能)为树的第一层、“从右端打结”(有A1与B1、B1与C1、A1与C1打结3种可能)为树的第二层。

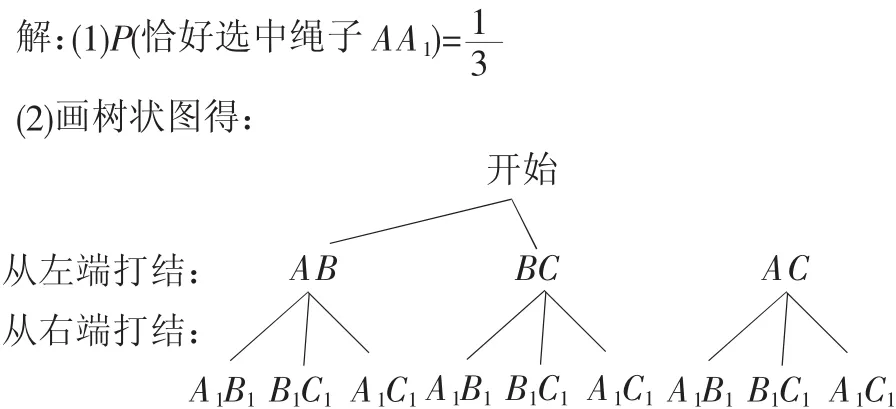
因此，所有可能的结果共有9种，其中能连结成一根长绳的情况有6种：

运用“动作分层法”解概率题，学生只要把题中游戏设计的“动作”挖掘出来，理清每个“动作”的可能结果，并按“动作”的先后顺序进行分层，即可快速、准确地画出树状图，从而解决问题。

(作者单位：江西省赣州市南康区大坪中学341418)

G633.6

A

1992-7711(2016)12-0105

刘伏文，男，任教于江西省赣州市南康区大坪中学，中学一级教师。