算子乘积的{1，2，3}－逆逆序律

张海燕， 司红颖

算子乘积的{1，2，3}－逆逆序律

张海燕， 司红颖

(商丘师范学院数学与信息科学学院，河南商丘476000)

借助特殊的空间分解，研究算子乘积的广义逆序律问题，给出当算子A、B、AB为闭值域算子时，B{1，2，3}A{1，2，3}=AB{1，2，3}和B{1，2，4}A{1，2，4}=AB{1，2，4}分别成立的充要条件．

分块算子矩阵;{1，2，3}－逆;逆序律

0 引言

为方便描述，首先介绍一些符号．用H和K表示无限维Hilbert空间，B(K，H)表示从K到H中的有界线性算子全体，当K=H时，将B(K，H)简记为B(H)．给定算子A∈B(H，K)，用N(A)和R(A)分别表示算子A零空间和值域空间．对算子G∈B(K，H)，若满足下列方程中的一个或者几个均称G为A的广义逆:

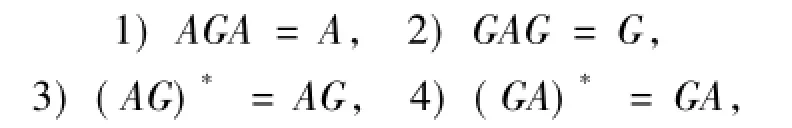
记A{i，j，…，l}为满足方程(i)，(j)，…，(l)的算子的集合．算子G∈A{i，j，…，l}称为算子A的{i，j，…，l} － 逆，有 时 也 记 为 A(ij…l)．算 子 A 的{1，2，3，4}－逆 A+是唯一的，被称为算子 A的Moore－Penrose逆或伪逆．方程(i)又称为Moore－Penrose方程或Moore－Penrose条件．

近几十年来，广义逆理论已成为很有用的工具，在数理统计、最优化控制、数值分析、微分方程等领域中有着广泛应用［1］，对多个矩阵或者算子乘积的广义逆的逆序律及其相关问题受到了很多学者的关注［2－18］．T．N．E．Greville［2］给出了一个较为经典的结果，指出(AB)+=B+A+当且仅当R(A*AB) R(B)且R(BB*A*) R(A*)，其中A和B为复矩阵，该结果被文献［3－4］推广到A、B为无限维Hilbert空间上的有界线性算子仍然成立．

随后，很多学者着手对各类广义逆的逆序律进行研究．文献［5］利用一种特殊的空间分解研究算子乘积的{1，3，4}－逆序律问题．文献［6］利用类似的方法刻画{1，2，3}－和{1，2，4}－逆的逆序律问题，给出B{1，2，i}A{1，2，i} AB{1，2，i}(i=3，4)成立的充要条件，而在矩阵代数中，B{1，2，i}A {1，2，i}=AB{1，2，i}(i=3，4)成立的充要条件在文献［7］中得到刻画．

本文主要利用分块算子矩阵技巧，将文献［7］中相关结果推广到无限维Hilbert空间中去，研究2个算子乘积的{1，2，3}－和{1，2，4}－逆的逆序律问题，给出当A、B、AB都为闭值域算子时，B{1，2，3}A{1，2，3}=AB{1，2，3}和B{1，2，4}A{1，2，4} =AB{1，2，4}分别成立的充要条件．

1 单个算子的{1，2，3}－逆

设算子A∈B(H，K)是闭值域算子，则算子A在空间分解H=R(A*) N(A)与K=R(A) N(A*)下有矩阵分解形式

其中A1∈B(R(A*)，R(A))可逆．众所周知，A的Moore－Penrose逆存在当且仅当A的值域是闭的，且此时A+有矩阵分解形式

算子A的{1，2，3}－逆也有类似的表现形式．在这一部分当中，探讨在特定的空间分解下算子的{1，2，3}－逆的一般矩阵形式．

引理1 设A∈B(H，K)是闭值域算子．若A关于空间分解H=H1H2H3与K=K1K2K3有矩阵形式

其中A11是可逆的且A22是满射算子，则A的{1，2，3}－逆A(123)有如下分解形式

其中G31∈B(K1，H3)及G32∈B(K2，H3)是任意的，Gji∈B(Ki，Hj)(i，j=1，2)满足

特别地，若N(A22)≠{0}，则满足条件2)的G21不唯一．

证明 令G∈A{1，2，3}，可设G在空间分解K =K1K2K3与H=H1H2H3下有如下矩阵形式

因此

结合(3)式和Moore－Penrose条件3)(AG)*=AG有

由此将(3)式代入Moore－Penrose条件1)AGA=A有

其中，x1代表A11，y1代表G11，x2代表A12，y2代表G21，x3代表A22，y3代表G22，y4代表G12，所以有

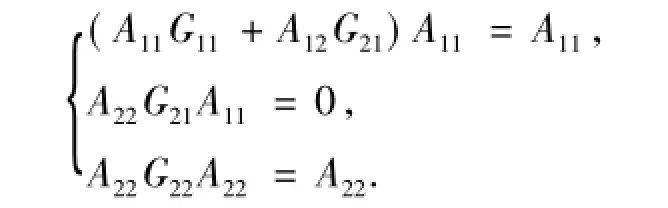
因为A11是可逆算子，所以

又结合A22G21=0，(3)式和Moore－Penrose条件3)知，A11G12+A12G22=0，因此 G12= －A－111A12G22．此时，AG的矩阵形式应为

将此式代入Moore－Penrose条件2)GAG=G得

因此，G13=0，G23=0，G33=0，G31∈B(K1，H3)是任意的，且有G22A22G22=G22．结合G22∈A22{1}与(4)式中(A22G22)*=A22G22知，G22∈A22{1，2，3}．又因为A22为满射算子，则A22G22=IK2．从而由(5)式可以看出G32可以为K2到H3中的任意有界线性算子．证毕．

特别地，若在引理1中K2={0}，容易得出下面结论．

引理2 设A∈B(H，K)是闭值域算子．若A关于空间分解H=H1H2H3与K=K1K2有矩阵形式

其中A11是可逆的，则A的{1，2，3}－逆A(123)有如下分解形式其中G21∈B(K1，H2)及G31∈B(K1，H3)是任意的，

其中G21∈B(R(A)，N(A))是任意的．

2 算子乘积的{1，2，3}－逆的逆序律

推论1 设A∈B(H，K)是闭值域算子并具有矩阵形式(1)，则A(123)具有如下矩阵分解形式

文献［7］主要利用矩阵行列变换研究矩阵乘积的{1，2，3}－逆的逆序律．在这一部分中主要利用算子分块技巧研究无限维Hilbert空间上闭值域算子乘积的广义逆序律．给出当A、B、AB都是闭值域算子时，AB{1，2，3}=B{1，2，3}A{1，2，3}成立的充要条件，并以此推断AB{1，2，4}=B{1，2，4}A {1，2，4}成立的等价条件．

定理1 设A∈B(H，K)，B∈B(K，H)，若A、B、AB都是闭值域算子，则AB{1，2，3}=B{1，2，3} A{1，2，3}的充要条件为R(A*AB) R(B)，且R(A)=R(AB)或R(B)∩N(A)={0}．

证明 为方便其见，首先给出一些记号，设

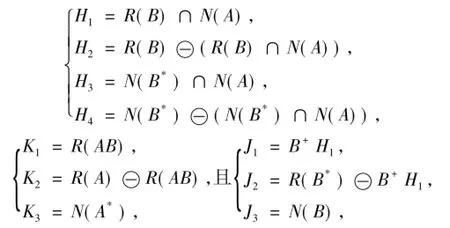
其中B+是B的Moore－Penrose逆，则H=H1H2H3H4且K=K1K2K3．接下来的证明分3种情况．

(i)H2={0}，则此时有R(B) N(A)，从而AB=0且有AB{1，2，3}={0}．

断言1 B{1，2，3}A{1，2，3}=AB{1，2，3}当且仅当A=0或B=0．

如果A=0或B=0，那么B{1，2，3}A{1，2，3} =AB{1，2，3}自然成立．假设A和B均不为零算子，则空间H可以正交分解为H=R(A*) R(B) ((N(A) R(B))，那么算子A和B有矩阵分解形式

其中A11、B21是可逆算子．根据推论1可知，算子A和B的{1，2，3}－逆的矩阵分解形式分别为

其中G21∈B(R(A)，R(B))，G31∈B(R(A)，N(A) R(B))，F21∈B(R(B)，R(B*))为任意算子．

所以

而此种情况下AB{1，2，3}={0}，结合已知B{1，2，3}A{1，2，3}=AB{1，2，3}，有B(123)A(123)=0．从而且FG=0．而假设B≠0，知B≠0．从122121而G21=0．另一方面由推论1知对任意的G21都能使(6)式为A的{1，2，3}－逆，所以只能A=0，这与假设矛盾．故若B{1，2，3}A{1，2，3}=AB{1，2，3}，则A=0或B=0，因此断言1成立．

断言2 R(A*AB) R(B)，且R(A)=R(AB)或R(B)∩N(A)={0}，当且仅当A=0或B=0．

充分性显然成立．只需说明必要性．若R(A)= R(AB)，而此时AB=0，则R(A)=0，即有A=0．若R(B)∩N(A)={0}，而此时R(B) N(A)，则R(B)=0，即有B=0，故断言2成立．结合断言1，知此情况下结论成立．

(ii)H2≠{0}，且H1≠{0}即R(B)∩N(A)≠{0}．此时A与B有矩阵表示形式如下

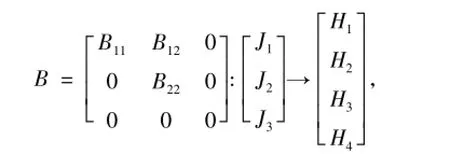
其中，A12、B11、B22是可逆算子，A24是满射算子，从而

由推论1及引理1知，B和A的{1，2，3}－逆分别具有以下矩阵形式

且

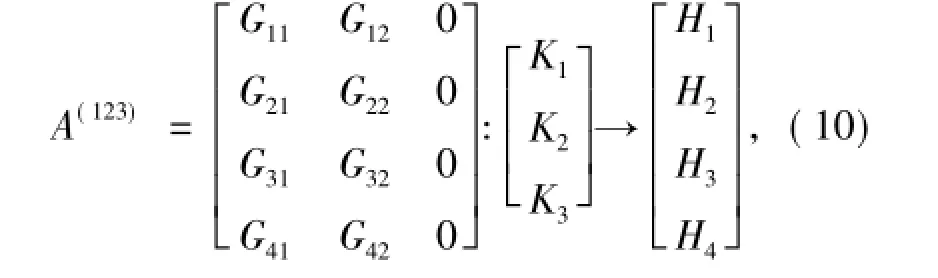
其中，F31、F32及Gij，i∈{1，3}，j∈{1，2}是任意的，且Gij，i∈{2，4}，j∈{1，2}满足

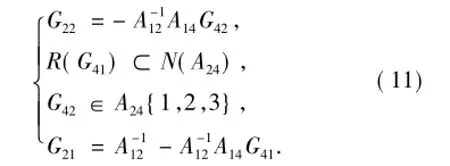
记

于是有

另一方面，结合AB的分解式(8)，由推论1知

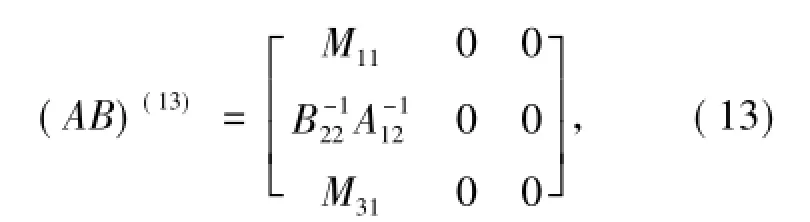
其中M11、M31是任意的．

假设B{1，2，3}A{1，2，3}=AB{1，2，3}，那么在相同的空间分解下，对任意的B(123)A(123)应具有(AB)(13)的矩阵分解形式，对比(12)和(13)式得

据引理1，(10)式中的G12是可以任意的，因此此时只能有K2={0}，即有R(A)=R(AB)，则此时A的矩阵分解式(7)中A24=0，又从而A14G41=0，所以R(G41) N(A14)．根据引理2知，G41是任意的，结合H4的定义知，A14=0，结合(9)式知，R(A*AB) R(B)．

反之，若R(A*AB) R(B)且R(A)=R(AB)，则有K2={0}且A的分解式(7)中A24=0，A14=0．因此结合引理2知，(11)式中G22=0，G42=0，G21=是任意的，并且 G =0，因此(12)式中的12P12=0，B－1

22G22=0，P32=0，且P11、P31可取任意的有界线性算子．对比(12)与(13)式可知，B{1，2，3}A {1，2，3}=AB{1，2，3}成立．

(iii)H2≠{0}但H1={0}，显然有J1={0}，则此时有R(B)∩N(A)={0}且H=H2H3H4且K=J2J3，那么A、B的矩阵形式为

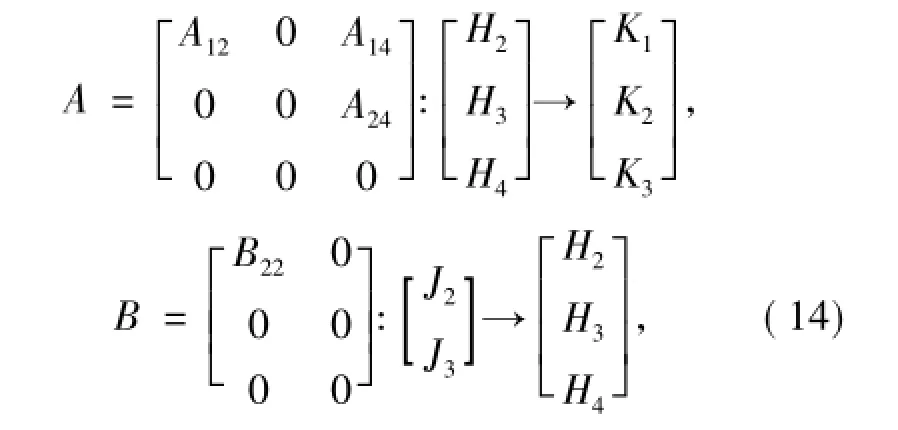
其中，A12、B22是可逆的，A24是满射算子．

从而

由推论1及引理1知，AB、B、A的{1，2，3}－逆分别具有以下矩阵形式:

且

其中，M31、F31、F32及Gij，i∈{1，3}，j∈{1，2}是任意的，且Gij，i∈{2，4}，j∈{1，2}满足

于是有

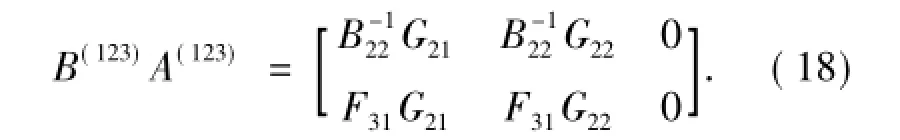
假设B{1，2，3}A{1，2，3}=AB{1，2，3}，对比(16)和(18)式得

反之，若R(A*AB) R(B)，则由(15)式知在(14)式中A14=0．据H4的定义可知，A24可逆，则在(17)式中，．代入(16)与(18)式做对比可知，B{1，2，3}A{1，2，3} =AB{1，2，3}．证毕．

由定理1的证明过程可知下述结果成立．

注1 设A∈B(H，K)，B∈B(K，H)为闭值域算子且AB也是闭值域的，则AB{1，2，3} B{1，2，3}A{1，2，3}恒成立．

由广义逆的4个Moore－Penrose的条件可以看出，若算子G是算子A的{1，2，3}－逆，那么G*一定是算子A*的{1，2，4}－逆，根据{1，2，3}－逆与{1，2，4}－逆的这种对偶关系容易得出下面的结论成立．

定理2 设A∈B(H，K)，B∈B(K，H)为闭值域算子且AB也是闭值域算子，则下列命题等价:

由算子的{1，2，3}－逆，{1，2，4}－逆与其Moore－Penrose逆的关系，结合定理1和2，下面给出算子乘积Moore－Penrose逆序律成立的一个充分条件．

推论2 设A∈B(H，K)，B∈B(K，H)为闭值域算子且 AB也是闭值域算子，若 R(A*AB)= R(BB*A*)，且R(A)=R(AB)或R(B)∩N(A)= {0}成立，则(AB)+=B+A+．

证明 因为 R(A*AB)=R(BB*A*)，即有R(A*AB) R(B)，根据定理1可知，AB{1，2，3}= B{1，2，3}A{1，2，3}，所以有B+A+∈AB{1，2，3}．

接下来对应定理1的证明过程中的3种情况分别说明:

(i)H2={0}，此时有A=0或者B=0，则结论自然成立;

(ii)H2≠{0}，且H1≠{0}，此时A与B有矩阵表示形式如下:

其中，A12、B11、B22是可逆算子，从而有

对比A*与B*的矩阵形式可知，R(A*)∩N(B*)= {0}，而又知R(BB*A*)=R(A*AB) R(A*)，所以根据定理2，可知AB{1，2，4}=B{1，2，4}A{1，2，4}成立，则B+A+∈AB{1，2，4}，前面已证B+A+∈AB{1，2，3}，从而(AB)+=B+A+．

(iii)H2≠{0}但H1={0}，此时有

根据A12、B22的可逆性，可以得出此时 R(B*)= R(B*A*)．而已知R(BB*A*)=R(A*AB)，所以根据定理2，可知AB{1，2，4}=B{1，2，4}A{1，2，4}成立，故B+A+∈AB{1，2，4}，所以(AB)+=B+A+成立．证毕．

这里推论2的条件只是充分条件而非必要条件．

例1 设H为实Hilbert空间，算子A、B为空间H H H的有界线性算子，其具体形式为

其中I为H上的单位算子，通过直接计算可得

而

所以AB{1，2，3}≠B{1，2，3}A{1，2，3}．

3 结语

本文主要是利用了特殊的空间分解对闭值域算子进行分块处理，由此研究集合AB{1，2，3}与B{1，2，3}A{1，2，3}相等的充要条件．利用类似的分解方法也可以刻画算子乘积的Moore－Penrose逆的逆序律成立等价条件［8］以及Moore－Penrose逆的乘积B+A+与集合AB{1，2，3}的关系．那么类似的方法是否可以适用于探讨更多个算子乘积的广义逆序律呢?这个问题将有待于进一步探讨．

［1］WANG G，WEI Y，QIAO S．Generalized Inverses:Theory and Computations［M］．北京:科学出版社，2004．

［2］GREVILLE T N E．Note on the generalized inverse of a matrix product［J］．SIAM Rev，1966，8(4):518－521．

［3］BOULDIN R H．The pseudo－inverse of a product［J］．SIAM J Matrix Anal Appl，1973，24(4):489－495．

［4］IZUMINO S．The product of operators with closed range and an extension of the reverse order law［J］．Tohoku Math J，1982，34(2):43－52．

［5］王洁，张海燕，吉国兴．两个算子乘积的一种广义逆序律［J］．陕西师范大学学报(自然科学版)，2010，38(4):13－17．

［6］LIU X J，WU S X，CVETKOVIC－LLIC D S．New results on reverse order law for{1，2，3}and{1，2，4}－inverses of bounded operators［J］．Math Comput，2013，82(283):1597－1607．

［7］张凤霞，李莹，赵建立．两个矩阵乘积的{1，2，3}－逆和 {1，2，4}－逆的反序律［J］．山东大学学报(理学版)，2011，46(4):78－81．

［8］张海燕．算子乘积的Moore－Penrose逆序律［J］．数学的实践与认识，2014，44(11):260－264．

［9］CVETKOVIC－LLIC D S，HARTE R．Reverse order law in C*－algebras［J］．Linear Algebra and Its Applications，2011，434(5):1388－1394．

［10］DJORDJEVIC D S，DINCIC N C．Reverse order law for the Moore－Penrose inverse［J］．J Math Anal Appl，2010，361(1): 252－261．

［11］杜鸿科．线性算子广义逆的逆序律与Ep算子［J］．陕西师范大学学报(自然科学版)，1984，8(1):11－19．

［12］DENG C Y．Reverse order law for the group inverses［J］．J Math Anal Appl，2011，382(2):663－671．

［13］武淑霞，刘晓骥．C*－代数上的广义逆序律［J］．山东大学学报(理学版)，2011，46(4):82－85．

［14］LIU X J，HUANG S W，CVETKOVIC－LLIC D S．Mixed－type reverse－order laws for{1，3，4}generalized inverses over Hilbert spaces［J］．Appl Math Comput，2012，218(17):8570－8577．

［15］XIONG Z P，ZHENG B．The reverse order laws for{1，2，3}－and{1，2，4}－inverses of a two－matrix product［J］．Appl Math Lett，2008，21(7):649－655．

［16］XIONG Z P，QIN Y Y．A note on the reverse order law for least square g－inverse of operator product［J］．Linear and Multilinear Algebra，2016，64(7):1404－1414．

［17］付石琴，刘晓冀．广义逆算子乘积的不变性［J］．四川师范大学学报(自然科学版)，2016，39(3):185－190．

［18］王宏兴，刘晓冀．整环上矩阵的加权广义逆［J］．四川师范大学学报(自然科学版)，2009，32(6):734－737．

Reverse Order Laws for{1，2，3}-inverse of Two-operator Product

ZHANG Haiyan， SI Hongying

(College of Mathematics and Information Science，Shangqiu Normal University，Shangqiu 476000，Henan)

In this paper，we investigate the reverse order laws for{1，2，3}-inverse of two-operator product by making full use of block-operator matrix technique．When A，B，AB are closed range operators，the equivalent conditions for B{1，2，3}A{1，2，3}= AB{1，2，3}and B{1，2，4}A{1，2，4}=AB{1，2，4}are presented．

block-operator matrix;{1，2，3}-inverse;reverse order law

O177．1

A

1001－8395(2016)05－0671－07

10．3969/j．issn．1001－8395．2016．05．010

(编辑 郑月蓉)

2016－01－05

国家自然科学基金(11501345)、河南省自然科学基金(1523000410221)和河南省教育厅资助项目(14B110010)

张海燕(1980—)，女，副教授，主要从事算子理论与算子代数的研究，E－mail:csqam@163．com

2010 MSC:47A05;47A62