强磁场作用下原子扩散行为的研究进展*
丁 亮,牛 涛,张艳苓,覃继宁,范同祥,侯红亮
(1.上海交通大学金属基复合材料国家重点实验室,上海 201112;2.中航工业北京航空制造工程研究所,北京 100024)
强磁场是一种重要的外部物理条件,与普通电磁场的力效应和热效应不同,强磁场能够将强大的磁化能量无接触地传递到材料的原子尺度,明显改变材料的热力学状态,影响材料中原子和分子的排列、匹配、迁移等行为[1]。近年来,随着低温超导技术的快速发展,超导强磁场的获得日趋轻便、经济,强磁场装置的生产已达到产业化。目前,强磁场在控制材料的物理化学过程、相变、热处理、结晶凝固、液体悬浮与分离等方面均取得了大量的科研成果,发现了很多新现象或者制备新型功能和结构材料,并诞生了强磁场材料学。
扩散焊可以焊接其他方法难以焊接的材料,尤其是异种材料之间的结合,并且其接头显微组织和性能与母材接近,不存在气孔、宏观裂纹等缺陷。研究表明扩散焊中的许多过程,如固态相变、晶粒生长、晶界迁移以及再结晶等,都与扩散密切相关[2]。而研究发现,磁场对上述物理过程都有着重要影响[3-8]。然而由于原子扩散速率缓慢导致的工艺效率低下成为其主要弊端,限制了该技术的应用。因此,在技术角度探索通过施加强磁场来提高工艺效率,在科学角度研究强磁场下固态原子的扩散行为,具有十分重要的意义。
本文综述了目前国内外该领域的研究现状,重点分析了强磁场对扩散的影响机制,并对该领域存在的问题进行了归纳总结。
1 物理原理
磁场对物质主要有3种基本作用效果:磁化力、磁自由能和洛伦兹力[9]。其中,磁化力可见磁化力只有在梯度磁场或者磁化率分布不均匀的情况下存在。磁自由能密度由ωm=1/2χH2给出,对于常见顺磁物质,1T下能量密度约为10-6J/g,该值相对于原子的热振动可以忽略不计。磁场对固态物质的洛伦兹力作用,微观上主要表现在自由电子(尤其是在金属中),在磁场下的回旋效应,宏观上则表现为霍尔效应和磁致电阻,然而由于杂质和晶格热振动的强烈干预,该效应只有在强磁场、高纯度、极低温的条件下非常明显。对于带电的流体或者具有强导电能力的液态金属,其对流与磁场互相作用也会产生与运动方向相反的洛伦兹力作用,从而抑制对流运动,这种“电磁制动”的效果已经成功应用于连续铸造工业中,用来减少残留的熔渣,消除晶体缺陷,改善晶体质量。此外,对于铁磁性金属,磁场对其还有明显的磁致伸缩效应。
扩散是物质中原子或分子迁移的现象,同时也是固体中物质传输的唯一方式。从微观机制上来看,由于原子的热振动存在能量起伏,所以总会有部分原子具有足够高的能量,跨越势垒从原来的平衡位置跃迁到相邻的平衡位置,这就是原子的布朗运动,在化学势梯度的驱动下,宏观上最终表现出具有方向性的扩散现象。间隙原子主要通过间隙机制进行扩散,置换式固溶体中原子主要通过空位机制进行扩散,二者的扩散系数均有相似的阿伦尼乌斯公式的形式D=D0exp(-Q/(RT)),其中D0为扩散常数,Q为各自的扩散激活能,由于空位扩散需要额外的能量形成空位,故后者的扩散激活能除了势垒外,还包括空位形成能,这使得间隙扩散比空位扩散更容易,同时也更容易受外加条件的影响。试验上确定扩散系数一般采用波尔兹曼-俣野作图法求解菲克第二定律,具体方法如下:(1)通过引入变量到菲克第二定律得到解析解;(2)利用EPMA得到相应元素的浓度-距离曲线;(3)对该曲线作图得到解析解需要的参数;(4)代入参数求解。为降低误差,相邻浓度点的距离应尽可能小。
2 强磁场对间隙扩散的影响
目前国内外对于强磁场对间隙扩散影响的研究主要集中在低碳钢的脱碳上。Nakamichi等[10]率先在6T的磁场条件下研究0.09%C低碳钢的脱碳行为,发现在平行于磁场方向上,C在γ-Fe中的扩散系数最多有近50%的降低。由于间隙扩散对于晶格常数的变化比空位扩散更敏感[11],同时对于铁磁性物质,弹性模量-温度曲线在居里点附近有一个跳跃,因此作者认为外加磁场下铁磁性物质的磁有序导致晶格紧缩,引起跳跃原子需要跨越的势垒增加,扩散系数进而降低。此外,磁致收缩也会导致晶格紧缩。因此最终将磁场对间隙扩散的抑制作用归结于扩散激活能的增加。
Fujii等[12]在 850~1200K 温度范围内,利用 Fe-Fe/0.87%C扩散偶,发现在平行于6T的强磁场方向上,C在Fe中的扩散系数有70%~80%的降低。通过对C扩散系数进行Arrhenius 作图,得到不同磁场条件下扩散激活能:0T和6T下分别为(117±12)kJ/mol和(112±12)kJ/mol。这表明扩散系数的降低是由扩散常数引起而并非因为扩散激活能的提高。为解释该现象,作者结合McLellan等提出的C在Fe中间隙扩散的“双占位”模型,认为在强磁场下,由于α-Fe点阵的<100>方向在磁致伸缩的作用下被拉伸,使 C原子在八面体位置的占有率提高,但C原子在α-Fe中有3种扩散路径:O-Te-O、Te-O-Te和Te-Te,其中O和Te分别代表晶格的八面体和四面体位置,因此总的扩散系数是3者线性叠加:D=φODO-Te-O+(1-φO)×[φTeDTe-Te+(1-φTe)DO-Te-O],其中φO和φTe分别代表八面体和四面体位置被溶质原子占据的百分比,最终计算结果如图1所示。
Wang等[13]在1273K、12T的强磁场条件下,研究了Fe-Fe-0.76%C扩散偶的扩散行为。结果发现在扩散方向垂直于磁场方向时,强磁场对C原子的扩散有很明显的抑制作用,当二者平行/反平行时,强磁场表现出轻微的促进作用。给出的可能原因是两方面综合作用的结果:磁场导致奥氏体磁自由能的降低随C含量变化;Fe原子间磁偶极子的作用强度在平行于磁场和垂直于磁场方向不同。此外, Zhou等[14]通过测量强磁场下Fe-20Ni二元合金氧化层的厚度,发现强磁场抑制氧化层的生长。
从已有的研究结果看,强磁场对铁磁性金属中的间隙扩散起抑制作用,而且比较强烈。尽管处于居里点之上,但铁磁性金属的固有磁矩保留了下来,在强磁场下还是会表现出磁有序和磁致伸缩,后者在单晶中具有明显的各向异性。因此从影响机制上来看,强磁场很可能通过磁致伸缩影响溶质原子在不同位置(八面体、四面体位置等)的占有率而间接降低扩散系数,而并非通过影响扩散激活能,相关的计算证实了这一点[5]。然而由于缺乏强磁场下非铁磁性金属中间隙扩散的数据,还不能对最终的影响机制作出定论。
3 强磁场对空位扩散的影响
强磁场对扩散行为影响的研究,最早是从空位扩散开始的。Youdelis等[15-16]早在20世纪60年代便在2T、3T强磁场条件下对Al-Al/3%Cu 扩散偶进行扩散退火研究。成分的确定是通过测出不同位置的显微硬度,将硬度与成分一一对应得到的。试验结果显示,在垂直于扩散方向的3T磁场条件下,互扩散系数大约降低了25%,而平行于强磁场方向互扩散系数变化不大。为解释该试验结果,笔者将金属中自由电子气视为等离子体,并将扩散视为双极性扩散。根据等离子体动力学,垂直于磁场方向的等离子体的迁移率μ降低为未加磁场的 1/(1+ωce2τe2)倍[17],其中ωce=eB/m*和τce分别为回旋共振频率和碰撞频率,m*为电子的有效质量。再结合双极性理论:和,最终有:

其中,下标i和e分别代表离子实和电子。由于迁移率μ、碰撞频率τ和电子有效质量m*并无试验数据可用,只能给出估计值,计算结果如图2所示。
根据该计算,扩散系数降低25%,大概需要τce/m*为1017s·g-1,而这大概比铝的De Hass-van Alfen 试验值高两个数量级,可能的原因是活动离子实对价带结构的扰动或者扩散输送电子本身就具有较高的τce/m*值。
目前为止,对于强磁场下空位扩散的试验结果大都与上述结果相同,并归结于等离子体-双极性扩散理论。Li等[18]在10T的强磁场条件下,研究了Mg-Al扩散偶平行于磁场方向上中间相的生长,发现中间相的厚度随着强磁场的加入而降低。通过对相生长动力学的进一步研究发现,中间相厚度的降低与频率因子相关而与激活能关系不大。由于中间相厚度与原子扩散直接相关,最终归结于Youdelis等的等离子体动力学理论。
除此之外,Ren等[19]对Ni/Al扩散偶, Yuan等[20]对Ni/Ni-6.3%Al扩散偶以及Chen等[21]对Ni/Cu扩散偶均做了类似的研究,并且得出相同的结论,上述扩散体系的试验结果汇总如表1所示。
然而,Nakajima等[22]在扩散方向平行或垂直于4T强磁场中,均未发现63Ni在α或β-Ti中的扩散系数有明显变化。同样, Nakamichi等[10]也并未在Ti/0.09%C-γ-Fe中发现强磁场对扩散系数的影响。Li[23]、Liu[24]等分别在Al/Mg、Cu/Ni扩散偶中发现强磁场能够提高扩散系数,他们均认为强磁场引入的磁自由能使得扩散原子的化学势提高,进而带来额外的扩散原子流,宏观上表现出来扩散系数的提高和柯肯达尔效应的增强。具体的试验结果如表2所示。
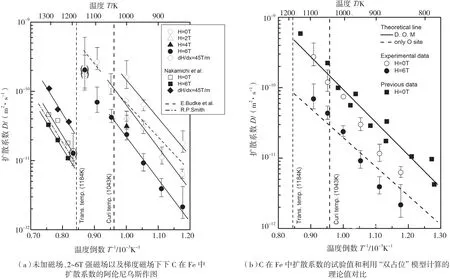
图1 强磁场下C在Fe中间隙扩散计算结果Fig.1 Interstitial diffusion calculation results of carbon in ferrum under high magnetic fields

图2 横向磁场下双极性扩散系数的变化Fig.2 Variation of the ambipolar diffusion coefficient in a transverse magnetic field
可见关于强磁场对空位扩散的影响,已有结果比较混乱。所用结果中,只有Li Donggang 等得到促进作用,其余均为无影响或抑制。从物质磁性的分类来看,涉及的合金体系有:顺磁-顺磁合金系,如Mg-Al、Ni-Ti、Ti-γ-Fe以及Ni-Al;顺磁-抗磁合金系,如Al-Cu和Ni-Cu。这里把Fe和Ni均视为顺磁物质是因为研究温度都处于居里点之上。从整体看,强磁场对于顺磁-抗磁合金系有抑制作用,对于顺磁-顺磁合金系,如若有Ti的存在,结果总是没有影响,除此之外为抑制作用。从这个角度来看,还无法就强磁场对空位扩散的影响结果做出结论,需要通过对更多的扩散体系进行试验验证。
从扩散的微观机制上来看,大部分学者均认为强磁场降低了扩散过程中原子跃迁频率和/或振动熵,从而降低了原子的自由度,延迟了原子扩散过程,而对扩散激活能的影响不大。Youdelis等提出的理论,本质上可以归结到强磁场对金属中自由电子的洛伦兹力作用,然而由于数据的缺乏,不足以做出最终定论;Li等[23]提出的磁自由能理论部分解释了自己的试验结果,然而在稳恒强磁场下,均匀介质中磁自由能应该是处处相同的,并不会导致化学势梯度而引起额外的扩散原子流,所以该理论也有待进一步改进。

表1 强磁场对中间相生成和长大的影响
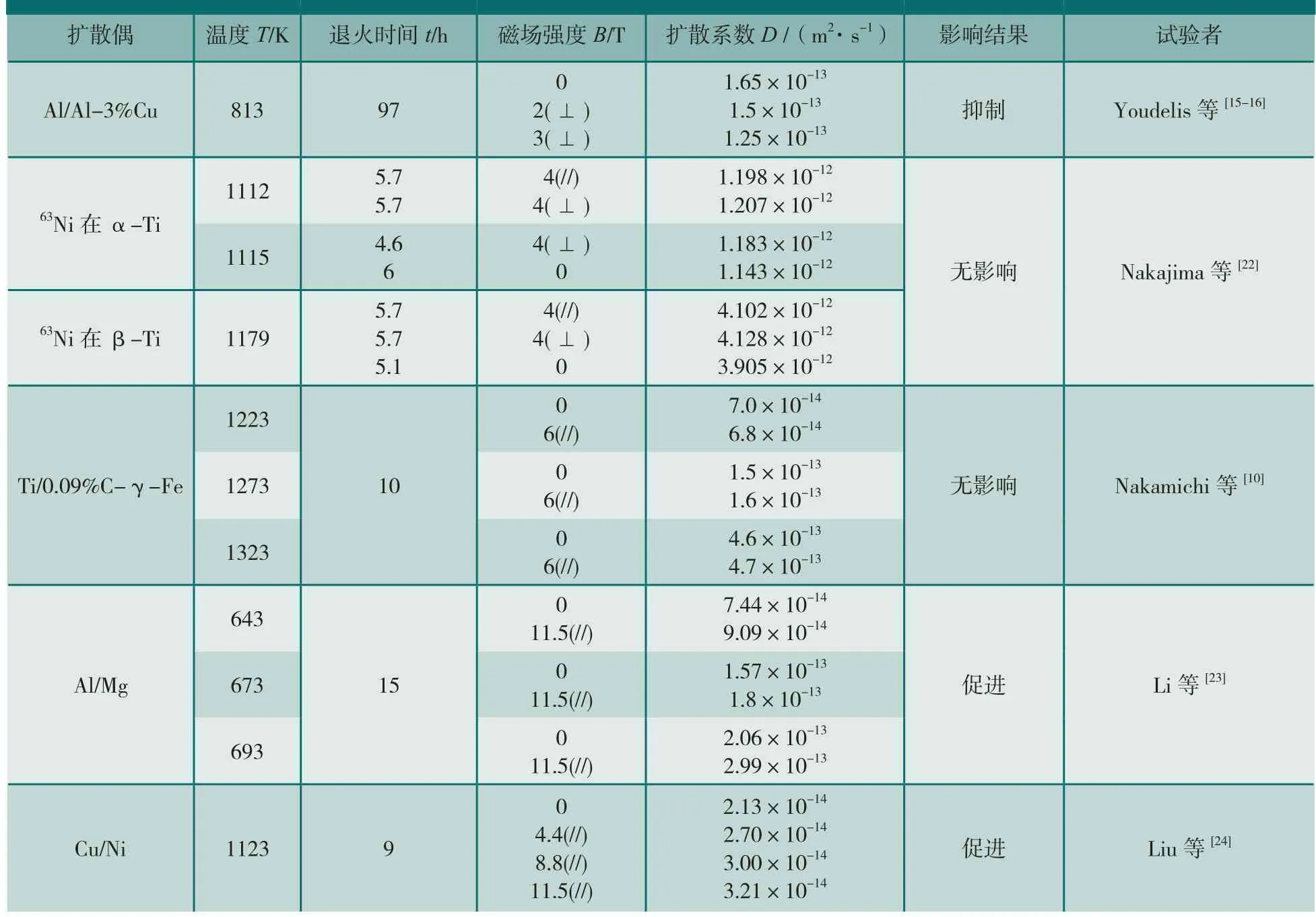
表2 强磁场对空位扩散系数的影响结果
4 结束语
从影响结果上来看,已有的试验结果均显示强磁场对铁磁性金属中溶质原子的间隙扩散起抑制作用,至于空位扩散,对于顺磁-抗磁合金系有抑制作用,对于顺磁-顺磁合金系,如若有Ti的存在,结果总是没有影响,除此之外为抑制作用;从影响机制上来看,二者均没有完善的理论定量地解释磁场大小和方向对于扩散的影响。因此还需要对更多类型的扩散偶进行定量的研究,在此基础上归纳出影响的一般规律,进而从理论上解释各种影响的物理机理。
随着低温超导技术的进步,强磁场在较大空间的实现变得更加经济轻便,发生装置日趋商业化。这使其应用范围从传统的铁磁性材料扩大到整个材料领域。扩散焊具有接头质量高、缺陷少、精度高、变形小等优点,并且可以实现难焊材料,尤其是异种材料的可靠连接。然而由于扩散焊需要较长的时间来达到冶金结合,而采用外加强磁场的方法可以控制原子能量状态,进而调节中间相、夹杂物、各种缺陷,从而影响整个扩散焊过程,加快扩散焊的进度,得到所需要的结果。这都需要从微观上探讨作用机理以正确指导其工业应用。因此,对强磁场作用下固态金属中原子扩散行为的研究,具有重要的科学意义和应用价值,必须引起足够的重视并加大投入。
[1]陈东风,曹志强,杨淼,等. 强磁场在材料科学中的应用现状及理论分析[J]. 钢铁研究,2007,35(3):58-62.
CHEN Dongfeng, CAO Zhiqiang, YANG Miao, et al. Application situation and theoretical analysis of high magnetic field in material science[J]. Research on Iron and Steel, 2007,35(3):58-62.
[2]任晓. 强磁场作用下镍系合金元素扩散行为研究[D]. 大连:大连理工大学, 2010.
REN Xiao. Elements diffusion behavior of nickel system alloy under high magnetic field[D]. Dalian:Dalian University of Technology, 2010.
[3]KUSTOV S, CORRÓ M L, PONS J, et al. Entropy change and effect of magnetic field on martensitic transformation in a metamagnetic Ni-Co-Mn-In shape memory alloy[J]. Applied Physics Letters, 2009,94(19):1-3.
[4]INOUE K, YAMAGUCHI Y, ISHII Y, et al. Magnetic-fieldinduced martensitic transformation of off-stoichiometric single-crystal Ni2MnGa[J]. Journal of the Physical Society of Japan, 2009, 78(5):1-6.
[5]LUDTKA G M, JARAMILLO R A, KISNER R A, et al. In situ evidence of enhanced transformation kinetics in a medium carbon steel due to a high magnetic field[J]. Scripta Materialia, 2004, 51(2):171-174.
[6]HARADA K, TSUREKAWA S, WATANABE T, et al.Enhancement of homogeneity of grain boundary microstructure by magnetic annealing of electrodeposited nanocrystalline nickel[J]. Scripta Materialia,2003, 49(5):367-372.
[7]MOLODOV D A, BOLLMANN C, KONIJNENBERG P J, et al.Annealing texture and microstructure evolution in titanium during grain growth in an external magnetic field[J]. Materials Transactions, 2007,48(11):2800-2808.
[8]GUBERNATOROV V V, SYCHEVA T S, VLADIMIROV L R, et al. Effects of ion irradiation and magnetic field on primary recrystallization of metals[J]. The Physics of Metals and Metallography, 2009, 107(1):68-72.
[9]李东刚. 异质金属体系扩散行为和界面反应的强磁场控制研究[D]. 沈阳:东北大学, 2009.
LI Donggang. Study on the diffusion behavior and interfacial reaction of heterogeneous systems controlled by high magnetic metal fields[D].Shenyang: Northeastern University, 2009.
[10]NAKAMICHI S, TSUREKAWA S, MORIZONO Y, et al.Diffusion of carbon and titanium in γ-iron in a magnetic field and a magnetic field gradient[J]. Journal of Materials Science, 2005, 40(12):3191-3198.
[11]BUDKE E, HERZIG C H, WEVER H. Volume and grain boundary diffusion of 14C in α-Fe[J]. Physica Status Solidi(a), 1991,127(1):87-101.
[12]FUJII H, TSUREKAWA S,フジイ,ヒロミチ, et al. Diffusion of carbon in iron under magnetic fields[J]. Physical Review B Condensed Matter, 2011, 83(83):589-597.
[13]WANG S J, WU Y, ZHAO X, et al. Effect of a High Magnetic Field on Carbon Diffusion in γ-Iron [J]. Materials transactions, 2011,52(2):139-141.
[14]ZHOU C H, MA H T, WANG L, et al. Growth of subscale on Fe–20Ni binary alloy in the presence of magnetic field[J]. Corrosion Science, 2013, 77:292-296.
[15]YOUDELIS W V, COLTON D R, CAHOON J. On the theory of diffusion in a magnetic field [J]. Canadian Journal of Physics, 1964,42(11):2217-2237.
[16]YOUDELIS W V, CAHOON J R. Diffusion in a magnetic field[J]. Canadian Journal of Physics, 1970, 48(6):805-808.
[17]HOLT E H, HASKELL R E. Foundations of plasma dynamics[M]. New York: Macmillan, 1965.
[18]LI Z F, DONG J, ZENG X Q, et al. Influence of strong static magnetic field on intermediate phase growth in Mg-Al diffusion couple [J].Journal of Alloys and Compounds, 2007, 440(1):132-136.
[19]REN X, CHEN G Q, ZHOU W L, et al. Effect of high magnetic field on intermetallic phase growth in Ni-Al diffusion couples [J]. Journal of Alloys and Compounds, 2009, 472(1):525-529.
[20]YUAN Z, REN Z, LI C, et al. Effect of high magnetic field on diffusion behavior of aluminum in Ni-Al alloy [J]. Materials Letters, 2013,108:340-342.
[21]CHEN G, REN X, ZHOU W, et al. Atomic interdiffusion in Ni–Cu system under high magnetic field[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(8):2460-2464.
[22]NAKAJIMA H, MAEKAWA S, AOKI Y, et al. Diffusion of nickel in titanium in a magnetic field[J]. Trans. Jpn. Inst. Met., 1985,26(1):1-6.
[23]LI D, WANG K, WANG Q, et al. Diffusion interaction between Al and Mg controlled by a high magnetic field[J]. Applied Physics A, 2011,105(4):969-974.
[24]LIU T, LI D, WANG Q, et al. Enhancement of the Kirkendall effect in Cu-Ni diffusion couples induced by high magnetic fields[J].Journal of Applied Physics, 2010, 107(10):345-350.

