权值动态分配的加权平均法在姿态解算中的应用
江 杰,高 超,虞丽娜
(内蒙古科技大学信息工程学院,包头 014010)
捷联惯导系统是一种不依赖外部信息,也不向外辐射能量的自主导航系统,通过测量其载体或运动系统在惯性参考系中的加速度,并对其时间进行积分,变换至导航坐标系中,进而得到导航坐标系中的速度、偏角、位置信息等。因其对外界依赖性小、隐蔽性好的特点已广泛应用于交通运输、航空、航天、航海等领域。姿态解算算法是捷联惯导系统的核心技术之一。目前,姿态解算方法主要有欧拉角法、方向余弦法和四元数法,而其中每个算法都各有其优缺点,都存在一定的误差,解算精度也有所不同[1-5]。
随着多传感器数据融合技术的不断发展和进步,该技术在生产、生活、工业、军事、航空航天等诸多领域都有了非常广泛地应用。其中,在实际应用中最常见的主要包括以下几种数据融合的方法[6-11]:
(1)依据被融合对象的统计学相关特性和相关的概率模型进行数据估计的数据融合方法,包括贝叶斯估计、统计决策理论等;
(2)利用常用规则来进行推理的数据融合方法,包括模糊规则推理、产生式规则推理等理论方法;
(3)对被融合项直接进行融合的方法,包括加权平均法等。
针对单一姿态解算算法解算之后存在一定误差的问题,采用了在捷联惯导系统的姿态解算过程中运用加权平均法的解决方案。因为在应用加权平均法的过程中,每个被融合项的最优权值系数的大小取决于每个姿态解算算法对姿态进行解算而得出的角度解算误差方差[12],角度解算误差的方差取决于各个算法的角度解算误差,解算误差又取决于角度的真实值,而在实际应用中角度的真实值是不能准确获得的,因此角度解算误差方差这一数值同样是不能准确获得的。对于这个问题,本文提出了一个具有实际意义的解决方案,即由一种动态分配权值的方法[12-13]来对被融合对象的权值进行估算,然后将欧拉角法、方向余弦法和四元数法解得的角度进行加权平均融合,以提高单一算法的解算精度,并将此方法应用到姿态解算模块中验证其解算精度。
1 姿态解算算法
一般而言,在进行姿态解算时都要经过以下步骤:
(1)获得被解算载体的角速度或角增量(这里指的是对于选定的基准坐标系而言)。该值一般可以通过惯性器件直接获得,也可以通过动力学积分而来;
(2)选定某种姿态解算的方法获得姿态的四元数或者欧拉角等的相关信息,主要通过对步骤(1)中获得的角速度或角增量求积分而得到;
(3)通过相关计算求出姿态矩阵,得出姿态角。
其基本流程图如图1所示。
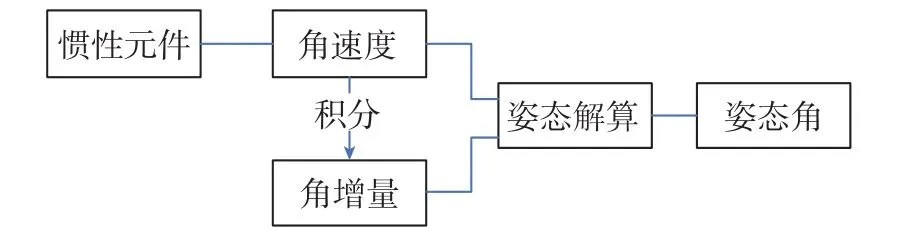
图1 姿态解算流程图Fig.1 Flow chart of attitude solution
1.1 欧拉角法
用欧拉角法求解姿态矩阵和姿态角,即是将运动学方程直接积分,需要求解3个参数,当俯仰角为 90°时,方程具有奇异性,滚动角和偏航角无法定值,而且积分的误差会不断累积,这就是应用欧拉运动学方程求解姿态矩阵方法的主要缺陷[1,3,5]。
1.2 方向余弦法
方向余弦法虽然无奇点,可用于全姿态解算,但是需要求解九个参数,计算量大,耗时较长,对内存要求较高[1,3,5]。
1.3 四元数法
四元数法需要求解4个参数,其计算无奇点,计算量小,工程中比较常用。但对于实时算法而言,应用四元数法却存在计算误差会随着计算次数的增多不断增大的问题,最终会使结果偏离真实值过大,甚至根本不能求解出结果[1,3,5]。
2 算法的加权平均融合
本文所用的最优权值分配原则与每种算法解算的姿态角度的均方差σi(i=1,2,3)有关。因此,要获得最优权值分配,首先必须知道解算的姿态角度的测量方差。而实际情况是,一般并不能获取到具体的σ值,对于此问题,本文首先实时地估算出每种算法解算出的姿态解算方差的值,依据最优权值的分配原则来分配每个解算结果的权值,最终将各个解算结果进行加权平均,以实现各解算结果的融合。基于真实角度值并非已知的前提,假设第i种算法在tk(k=1,2,…,N)时刻解算得到的姿态角度为Yi(i=1,2,3),那么就能够参考tk时刻各种算法解算角度的平均值来确定当前真实的角度值,而各种算法解算的姿态角度与平均角度值之间存在的差值就可以当作是其与真实角度值之间的差值,那么就能够得出单一算法解算的角度在tk时刻的角度偏差的方差,就能够依据最优权值分配的原则获得tk时刻的姿态角度的权值,进而得到加权平均融合之后的姿态角度,将其作为姿态解算模块的测量结果应用于定位导航中。
tk时刻各种算法解算角度的平均值为:

式中,Yi(k)为第 种算法在k时刻解算后的测量值。tk时刻各种算法解算的角度与平均值的偏差:

第i种算法在前面k次解算误差的平均值为:

在tk时刻第i种算法的解算误差的标准差为:

将式(4)解得的标准差看作是各角度解算均方差的近似,然后根据最优权值分配原则,就可以得tk时刻的权值:

接着可以得到tk时刻加权融合后的姿态角度为:
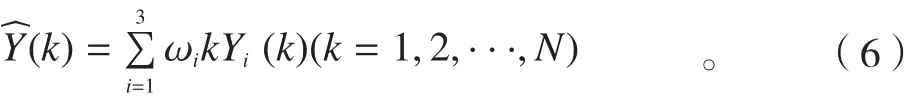
3 试验分析
为了检验这种动态分配权值的加权平均融合方法应用于捷联惯导系统的姿态解算中所得姿态角度的精度,本文将此方法应用于惯性元件MPU6050对姿态角的实际测量中进行试验验证,其中陀螺仪的量程设定为±1000°/s,主要依据三轴陀螺仪所测量的角速度值进行姿态解算。
本文以偏航角为例,设定其在-90°~+90°逐渐变化,随机选取其中几段时间内欧拉角法、方向余弦法和四元数法的解算误差曲线与融合之后解算误差曲线的对比,验证将这种动态权值分配的加权平均融合方法应用于姿态解算模块中进行姿态解算的可行性和有效性。
图2、3、4、5分别给出了随机选取试验过程中的一段时间内,单一算法与融合之后的解算误差曲线。
图6为各个算法误差曲线的汇总,其中黑色的曲线即是各种算法融合之后的误差曲线,可以清楚地看出将3种算法融合之后所得角度的误差要明显低于其中任何一种算法所得角度的误差,并且误差曲线也更加趋于稳定,这充分证明了这种权值动态分配的加权平均融合算法在姿态解算中有效地提高了解算精度,降低了解算误差。另外,对各解算结果进行数据分析,如表1所示。
由表中的数据分析结果表明,在同等条件下,加权平均得到的姿态角误差平均值低于任一单一算法,其标准差同样也低于任意单一解算算法的标准差。这也验证了,通过动态分配权值的加权平均法对姿态解算方法的解算结果进行融合是可行的。
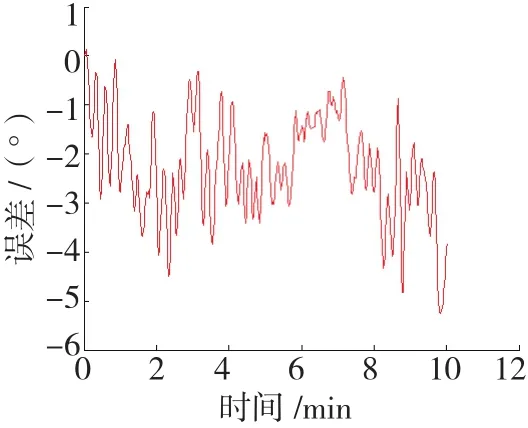
图2 偏航角为47°时方向余弦法解算误差曲线Fig.2 Solution error curve of direction cosine algorithm with yaw angle being 47°

图3 偏航角为47°时欧拉角法解算误差曲线Fig.3 Solution error curve of euler angle algorithm with yaw angle being 47°

图4 偏航角为47°时四元数法解算误差曲线Fig.4 Solution error curve of quaternion algorithm with yaw angle being 47°

图5 偏航角为47°时融合后的解算误差曲线Fig.5 Solution error curve after fusing with yaw angle being 47°

图6 偏航角为47°时误差曲线的对比图Fig.6 Comparison chart of solution error curve with yaw angle being 47°

表1 不同算法下偏航角度的误差统计 (°)
4 结论
本文给出了欧拉角法、方向余弦法和四元数法3种姿态解算方法,分别陈述了它们各自的优势和不足,并在捷联惯导系统的姿态解算中加入了加权平均的数据融合方法。对于实际中不能够得到真实的角度解算误差方差这一问题,提出了一种对角度解算误差进行实时估计并动态分配权值的方法,将欧拉角法、方向余弦法和四元数法解算所得角度进行加权平均融合。对单一算法的解算结果及融合之后的结果进行了试验分析,结果表明,融合后的解算精度比单一算法有了明显提高,可以将该种融合方法应用于姿态解算模块中进行姿态解算。
[1]杜海龙,张荣辉,刘平,等.捷联惯导系统姿态解算模块的实现 [J]. 光学精密工程, 2008, 16(10):1957-1962.
DU Hailong, ZHANG Ronghui, LIU Ping, et al. Realization of attitude algorithm module in strapdown inertial guidance system[J]. Optics and Precision Engineering, 2008, 16(10):1957-1962.
[2]张荣辉, 贾宏光, 陈涛, 等. 基于四元数法的捷联式惯性导航系统的姿态解算[J]. 光学精密工程, 2008, 16(10):1964-1970.
ZHANG Ronghui, JIA Hongguang, CHEN Tao, et al. Attitude solution for strapdown inertial navigation system based on quaternion algorithm[J].Optics and Precision Engineering, 2008, 16(10):1964-1970.
[3]李海涛. 加速度计/磁强计捷联惯导系统姿态解算方法研究[D].太原: 中北大学, 2007.
LI Haitao. Study on attitude algorithm of accelerometers/magnetometers strapdown inertial navigation system[D]. Taiyuan: North University of China, 2007.
[4]陈廷楠, 张登成. 双欧法与四元数法的应用比较[J]. 飞行力学 , 1996, 14(4):60-64.
CHEN Tingnan, ZHANG Dengcheng. Application comparision of dual euler method and quaternion method[J]. Flight Dynamics, 1996,14(4):60-64.
[5]杨志菊, 袁刚, 徐新林. 飞行器姿态解算方法及仿真研究 [J].辽宁工业大学学报(自然科学版), 2010, 30(5):307-309.
YANG Zhiju, YUAN Gang, XU Xinlin. Aircraft postures algorithm and their simulation study[J]. Journal of Liaoning University of Technology(Natural Science Edition), 2010,30(5):307-309.
[6]WALTZ L. Multi-sensor data fusion[M]. Massachusetts: Artech House, 1990:3-15.
[7]范晓静. 基于多传感器信息融合的机器人避障和导航控制研究[D]. 沈阳:沈阳理工大学, 2008.
FAN Xiaojing. Study of robot’s obstacle avoidance and navigation control based on multi-sensor information fusion technology[D].Shenyang:Shenyang Ligong University, 2008.
[8]赵敏华, 安毅生, 黄永宣. 多传感器信息融合技术在智能驾驶系统中的应用 [J]. 自动化与仪器仪表 , 2003, 29(1):30-32.
ZHAO Minhua, AN Yisheng, HUANG Yongxuan. Application of multi-sensor information fusion technology in intelligent drive system[J].Automation and Instrumentation, 2003, 29(1):30-32.
[9]THAWORNWONG S, ENKE D. The adaptive selection of financial and economic variables for use with artificial neural networks[J].Neuorcomputing, 2004, 56(1):205-232.
[10]BEAUVAIS M, LAKSHMANAN S. CLARK: a heterogeneous sensor fusion method for finding lanes and obstacles[J]. Image and Vision Computing, 2000,18(5):397-413.
[11]王淑芳, 任兰珍. 基于多传感器信息融合技术的智能驾驶系统模型 [J]. 北京石油化工学院学报 , 2006, 14(3):52-55.
WANG Shufang, REN Lanzhen. Intelligent drive system model based on multi-sensor information fusion technology[J]. Journal of Beijing Institute of Petro-chemical Technology, 2006, 14(3):52-55.
[12]凌林本, 李滋刚, 陈超英,等. 多传感器数据融合时权的最优分配原则 [J]. 中国惯性技术学报 , 2000, 8(2):37-39.
LING Linben, LI Zigang, CHEN Yingchao, et al.The optimal distribution principle of weight when multi-sensor data is fusing[J]. Journal of Chinese Inertial Technology,2000, 8(2):37-39.
[13]郝燕玲, 刘志平. 权值动态分配的 GFSINS 多角速度加权平均融合算法[J]. 中国惯性技术学报, 2010, 18(1):17-21.
HAO Yanling, LIU Zhiping. Fusion algorithm of angular velocity weighted averages for GFSINS based on dynamically allocating weights[J].Journal of Chinese Inertial Technology, 2010, 18(1):17-21.

