焊接结构的疲劳评定方法

张彦华，刘 娟，杜子瑞，陶博浩

（北京航空航天大学机械工程及自动化学院，北京 100191）

焊接结构的疲劳往往起源于焊接接头细节局部应力应变集中区域裂纹萌生和扩展。其中焊接接头细节疲劳裂纹的萌生由焊趾（或焊根等）应力集中区的局部应力应变状态所决定，而疲劳裂纹扩展则与裂纹（包括缺口效应在内）的局部应力强度因子相关，即局部应力强度因子是焊接接头区疲劳裂纹扩展的主要控制参量。因此，焊接结构和焊接接头的疲劳强度评定需要从不同层次结构尺度进行分析。目前，焊接结构或焊接接头疲劳强度的工程评定已发展了几种层次结构尺度的方法[1-3]，主要有名义应力评定方法、结构应力评定方法、局部应力应变评定方法和断裂力学评定方法。比较而言，名义应力评定方法又称为“整体法”， 局部应力应变和断裂力学评定方法称为“局部法”，结构应力评定方法是整体法与局部法之间的过渡。本文综合介绍了这几种方法在焊接结构疲劳评定中的应用。

名义应力评定方法

已有的研究表明，影响焊接接头疲劳强度的主要因素是应力范围和结构构造细节，其次是材料性质和焊接质量，而载荷循环特性的影响相对较小[4]。因此，以名义应力为基础的焊接结构疲劳设计规范通常是基于应力范围和结构细节分类进行疲劳强度设计[5]，焊接结构设计疲劳载荷应力范围ΔσD不得超过特定结构细节规定的疲劳许用应力范围[ΔS]，即

焊接构件的疲劳许用应力范围是根据疲劳强度的试验结果，在考虑一定的安全系数的情况下确定的。现行的焊接构件疲劳强度设计标准中一般规定未消除应力的焊接件的疲劳许用应力范围可忽略平均应力的影响，但疲劳许用应力范围的最大值不得高于静载许用应力。

名义应力评定方法是根据焊接结构细节的S-N曲线进行疲劳强度设计，包括无限寿命和有限寿命设计两种方法[6]。无限寿命设计法是采用焊接件S-N曲线的水平部分，即疲劳极限；有限寿命设计法使用的则是焊接件S-N曲线的斜线部分，即有限寿命部分。无限寿命设计时设计应力要低于焊接件疲劳极限，而有限寿命设计时设计应力一般高于焊接件疲劳极限，这时需要按照累计损伤理论来估算焊接结构总的疲劳损伤，因此，有限寿命设计要确定恒幅载荷作用下各类焊接结构细节的S-N曲线。

焊接接头的疲劳强度与接头构造形式存在相关性，不同焊接接头的疲劳强度可以用疲劳质量等级进行分类，焊接接头疲劳质量分级是将各种接头分为不同的缺口等级并且对各缺口等级规定不同的S-N曲线和工作寿命曲线。按照焊接件的构造、焊缝形式、加载情况及制造等级进行分类后，可采用一族许用应力或持久应力值不同的标准S-N曲线和工作寿命曲线来表征焊接件的疲劳质量等级，以此构成名义应力评定方法的基础。图1为对接接头和十字型接头的名义应力范围与循环次数的关系，表明对接接头和十字型接头具有不同的疲劳质量等级或疲劳许用应力。

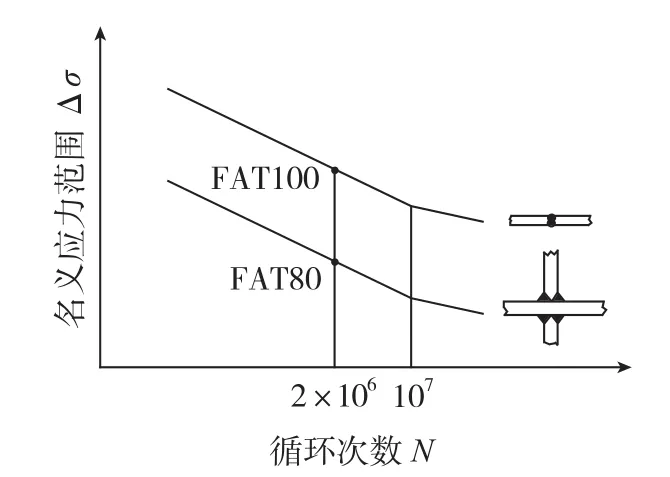
图1 对接接头和十字型接头的名义应力范围与循环次数的关系Fig.1 Relationship between the nominal stress range and the cycle number of butt joint and cross type joint

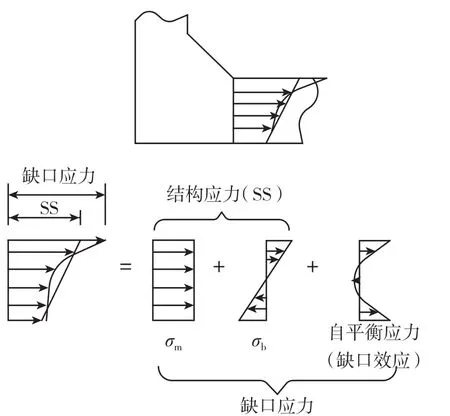
图2 焊趾区结构应力的分解Fig.2 Decomposition of structural stress in the weld toe area

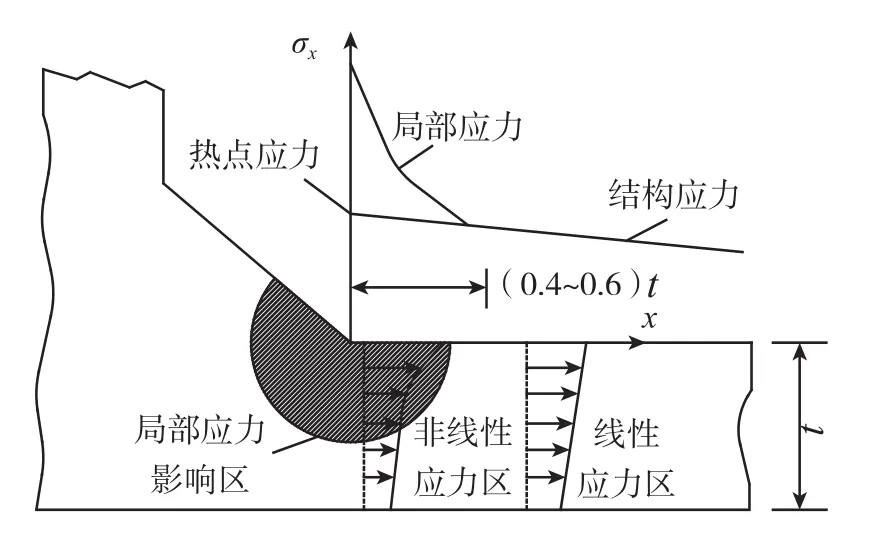
图3 热点应力的确定方法Fig.3 Methods of determining hot spot stress

目前，有关焊接结构疲劳设计和评定的相关规范大多采用名义应力表征焊接构件及接头的疲劳强度。基于焊接接头细节特征的焊接结构疲劳强度分类体系不断得到发展，焊接接头疲劳质量分级方法也不断完善，这对各类焊接结构疲劳强度的工程评定具有重要意义。

国际焊接学会提出的有关焊接结构和构件疲劳设计推荐标准建议将焊接接头的疲劳设计要求或内在疲劳强度用S-N曲线族来分级，分别表征不同焊接结构细节疲劳质量等级。所有级别的S-N曲线在双对数坐标系中互相平行，每条曲线的应力范围和循环次数的关系为：

式中，C为常数。

焊接件的疲劳质量等级依据疲劳寿命为2×106（循环次数N）所对应的应力范围S2×106进行确定。例如FAT125表示疲劳寿命为2×106时所对应的疲劳强度是S2×106=125MPa。

采用名义应力方法评定焊接结构的疲劳强度时，应根据焊接件的构造、受力方向和焊接工艺，选取合适的疲劳质量等级S-N曲线。由于各种结构设计标准不同，不同结构采用的焊接接头形式也存在很大差异，因此，对于复杂的焊接结构确定某一具体焊接接头究竟应该归于哪一个疲劳等级还是比较困难的。一般是根据疲劳危险区的主应力方向并结合该区域焊接接头的形式选择疲劳等级，同时要考虑焊接及其他处理工艺的影响。在设计阶段，结构中疲劳强度要求不高的区域可以选择较低级别的接头，疲劳强度要求高的区域就要选择较高级别的接头。在疲劳强度评定时，同等载荷条件下，要特别注意分析低级别接头的疲劳损伤。

结构应力评定方法

采用结构应力评定方法分析焊接结构疲劳强度时要求在名义应力计算的基础上进一步考虑焊接结构中的非均匀应力分布情况，因而需要对结构中的应力进行详细计算。焊接节点的结构应力是指接近焊趾或焊缝端部的局部应力，也可称为几何应力，结构应力的大小会受到焊接件整体几何参数的影响。一般而言，焊接接头局部区的应力分布具有高度的非线性，其结构应力的增大可用结构应力集中系数来表示：

式中，KS为结构几何引起的应力集中系数，σn为名义应力。

在结构应力不是很大的情况下，可采用厚度方向的应力分布线性化方法计算结构应力[7]。如图2所示，结构应力分析时将厚度方向上的缺口应力分离[8]，结构应力为:

其中，σS为结构应力；σm为薄膜应力；σb为弯曲应力。

结构应力的最大值又称为“热点应力”，“热点”一词来源于最大结构应力循环载荷所引起的局部热效应[9]。在大多数情况下，热点区的表面应力（不考虑缺口效应）即为结构应力。因此，通过在缺口效应不产生作用的构件表面一定区域内对结构应力进行线性外插，可确定“热点应力”（图3）。

根据热点应力评定焊接件疲劳强度的关键问题是如何获得焊接结构接头处的几何应力和以热点应力表征的S-N曲线。一般而言，只有在结构应力集中比较大的情况下，热点应力才适合作为焊接结构疲劳强度的评定参数，例如热点应力集中系数达10～20的管节点结构。

采用名义应力评定方法校核焊接结构疲劳强度需考虑焊接节点的结构形式，根据焊接节点形式选取相应的S-N曲线。对于形状复杂且难以准确定义名义应力的焊接接头，由于疲劳寿命的分散性大，很难建立精确的S-N曲线。采用结构应力或热点应力进行疲劳分析要建立不同结构细节 “共用”的S-N曲线（Shs-N曲线）。对于给定的材料，只要结构细节的热点应力相同，其疲劳强度就相当，不同热点应力的结构细节疲劳强度之间具有比例关系。若已知某结构细节的热点应力（称为参考热点应力σhs,ref）及疲劳等级（参考疲劳等级FATref），拟评定结构细节的疲劳等级 FATassess）为：

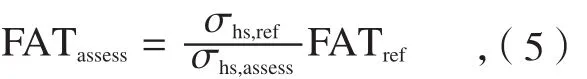
式中，σhs,assess为拟评定结构细节的热点应力，可采用前述的计算方法进行计算。这样就克服了名义应力法的不足，为各类结构细节的疲劳强度分析提供了方便。

应当指出，焊接构件的疲劳强度的因素在许多情况下不完全取决于结构应力而是缺口应力，而结构应力分析时却把缺口应力分离（图2）。因此，结构应力评定不能全面反映接头细节的疲劳行为，详细的疲劳分析还需要辅之以缺口应力分析。此外，结构应力评定方法目前仅适用于焊接接头焊趾区的疲劳分析，对于裂纹起始于焊根或未焊透等处的疲劳分析则受到限制。

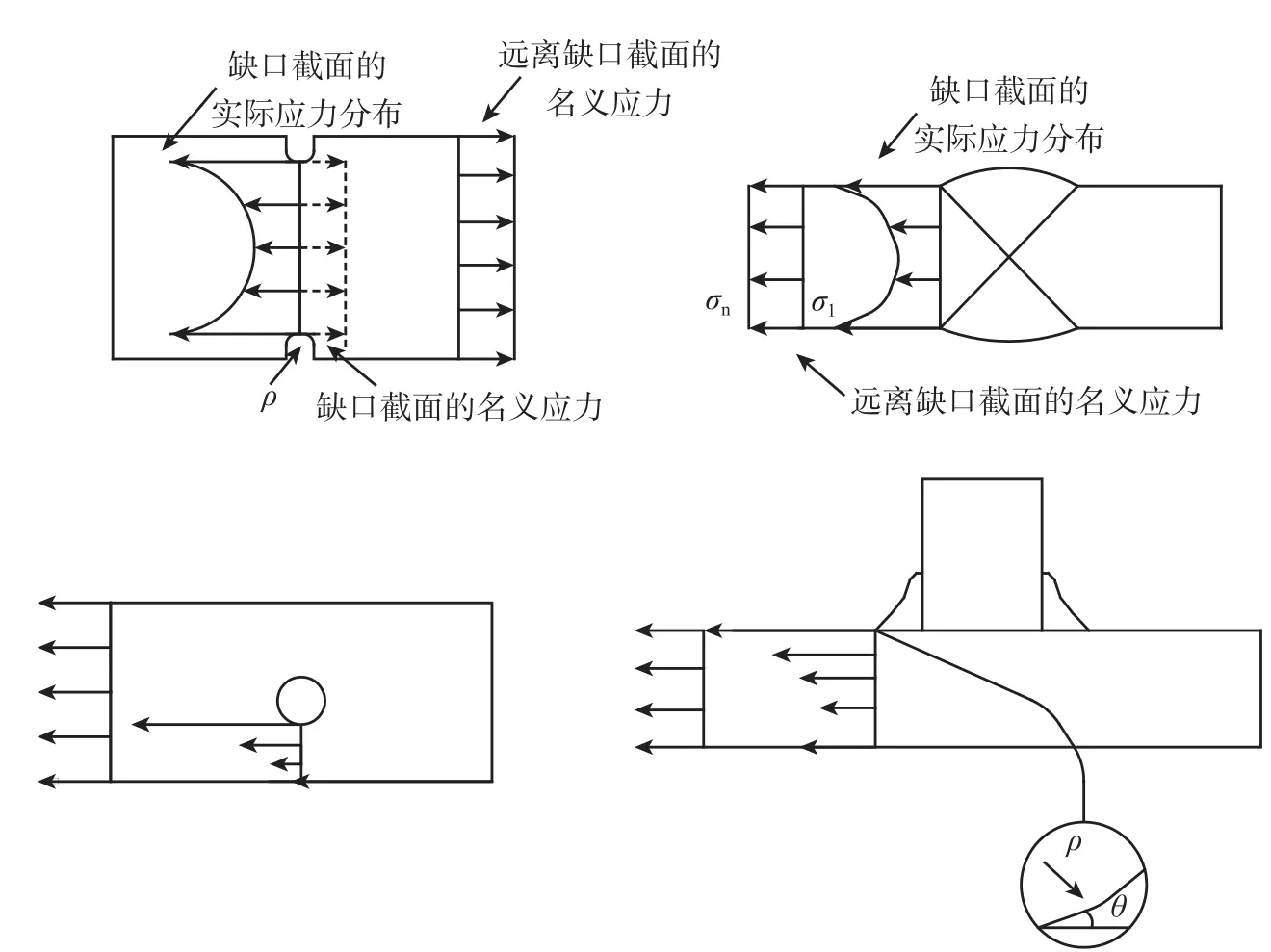
图4 焊接接头的缺口效应Fig.4 Notch effect of welded joint

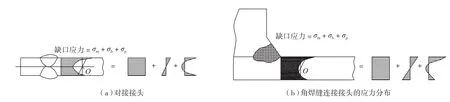
图5 焊接接头的缺口应力分布Fig.5 Stress distribution of welded joint

缺口应力应变评定方法

缺口应力评定方法是名义应力和结构应力评定方法的发展与延伸，这种方法认为焊接接头的疲劳破坏始于应力集中处的最大应力区，局部应力应变循环是疲劳裂纹萌生和扩展的条件，只要局部应力应变循环参量相同，其疲劳性能就相同。这种方法的原理是将应力集中区应力场的“局部参量”作为疲劳控制参量，建立“局部参量”与循环次数之间的关系[10]。

构件中的缺口是典型的应力集中问题，其他应力集中现象可以等效为广义缺口，应力集中对构件强度的影响称之为缺口效应。一般而言，缺口愈尖锐，应力集中系数愈大，应力梯度也愈大。焊接结构中因焊缝外形导致的应力集中对结构强度的影响，称为焊接接头的缺口效应（图4，ρ为缺口的曲率半径，θ为缺口角）。

缺口应力是焊接接头应力集中区的峰值应力，图5所示为焊趾缺口区正应力沿板厚方向的分布, 缺口应力可分解为膜应力（σm）、弯曲应力（σb）与非线性应力峰值（σp）。

在高周疲劳范围，缺口应力对于裂纹萌生和裂纹扩展的初始阶段虽不是唯一的影响因素，但往往是决定性因素。采用缺口应力范围可将不同接头类型的S-N曲线归一化，较结构应力评定方法更进一步[11]。

弹性缺口应力往往超过材料的屈服应力形成弹塑性区, 裂纹在塑性区中的扩展速率和在弹性区中的扩展速率有很大的不同，此时需要考虑缺口区的弹塑性应力应变。按照弹塑性缺口应力应变分析法的观点，若缺口顶端区的局部应力应变相同，则构件的疲劳寿命也必然是相同的。因此，对于具有应力集中的构件，可以根据光滑试样的应变-寿命（低周疲劳）曲线计算应力集中构件的疲劳寿命，当然也可以使用局部应力应变相等的试样进行疲劳试验来模拟（图6）。在获得构件应变集中区的局部应力应变和材料疲劳试验数据的情况下，依据这种方法便可以估算得到其裂纹萌生寿命，随后运用断裂力学方法可计算得出裂纹扩展寿命，裂纹萌生寿命与扩展寿命叠加即为构件的总寿命。

在焊接接头中，焊缝与母材连接过渡外形变化以及焊接缺陷都会引起应力集中而产生缺口效应（图7），可采用弹塑性缺口应力应变分析方法计算这类焊接接头的疲劳裂纹萌生寿命。应注意的是焊缝及热影响区的组织对ε-N曲线有较大影响，其裂纹萌生寿命亦有所差异。

应用局部应力应变法估算疲劳寿命需要对应力集中引起的局部应变进行分析。局部应变可根据Neuber法进行计算。图8给出了应用局部应力应变法对焊接接头疲劳进行分析的过程。

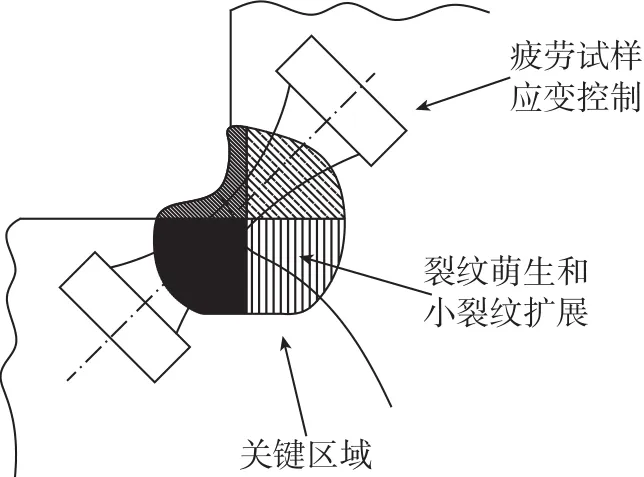
图6 局部应力应变法Fig.6 Local stress strain method

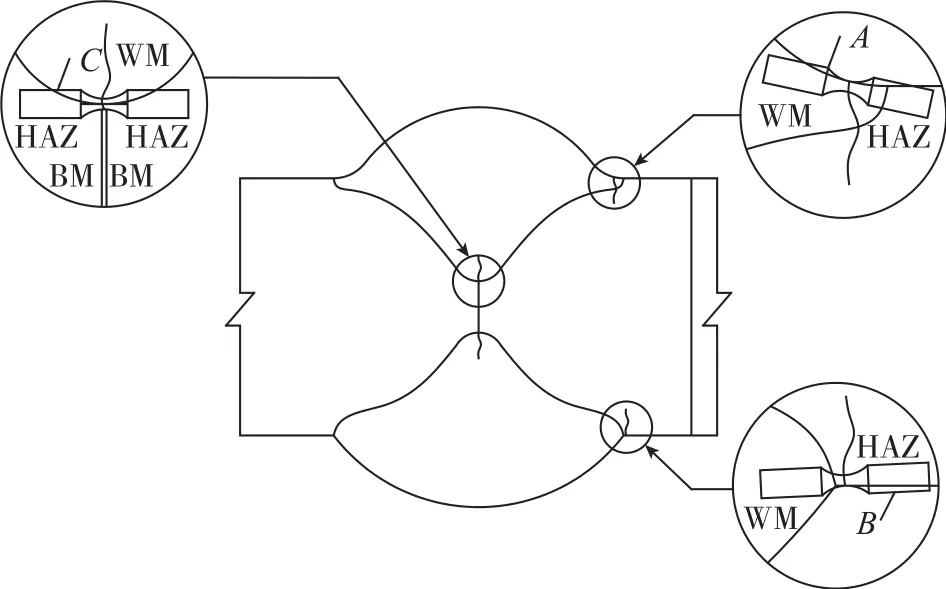
图7 焊接接头缺口应力应变模拟Fig.7 Simulation of notch stress and strain in welded joint

图8 局部应力应变法在焊接接头疲劳分析中的应用Fig.8 Application of local stress strain method in fatigue analysis of welded joint

应当指出，含缺口构件的疲劳强度不仅与缺口端局部最大应力应变存在相关性，缺口端有限区内的整体应力水平也会影响缺口构件的疲劳强度。采用这种方法进行焊接接头的疲劳强度分析需要较复杂的计算或测试，在实际应用和数据积累方面尚需要进一步加强。

断裂力学方法

依据断裂力学理论，当含有初始裂纹（长度为a0）的构件且承受静载荷时，若所受到的应力值达到了临界应力值σc，对应的裂纹尖端应力强度因子达到临界值KIC（或KC）时构件发生失稳破坏。若静载荷作用下的应力σ<σc，则构件不会发生破坏。但当构件受到疲劳载荷作用时（σ＞σc），其初始裂纹会缓慢扩展，一旦裂纹长度扩展到临界裂纹尺寸ac时就会发生失稳破坏。在循环应力的作用下，裂纹尺寸由初始裂纹长度a0扩展到临界裂纹长度ac的过程称为疲劳裂纹的亚临界扩展。疲劳裂纹亚临界扩展速率简称为疲劳裂纹扩展速率，用da/dN表示。一般情况下，疲劳裂纹扩展速率可以表示为

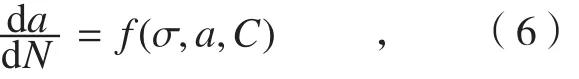
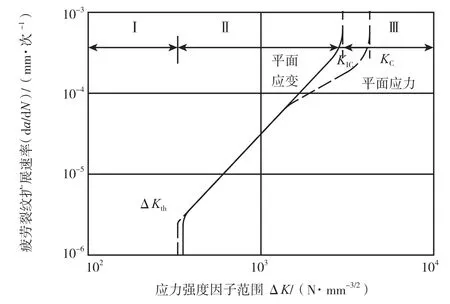
图9 da/dN-ΔK关系Fig.9 Relationship of da/dN-ΔK

式中，C为与材料有关的常数。

Paris的研究表明，应力强度因子K是控制疲劳裂纹扩展速率的主要力学参量[12]。由此建立了描述疲劳裂纹扩展速率的重要经验公式——Paris公式：

式中，ΔK为应力强度因子幅度（ΔK=Kmax-Kmin），Kmax和Kmin是与σmax和σmin分别对应的应力强度因子；C、m为材料常数，与环境、频率、温度和循环特性等因素有关。

在双对数坐标系中，da/dN～ΔK的关系曲线如图9所示，该曲线可分为低、中、高速率3个区域[13]，对应疲劳裂纹扩展的3个阶段，其上界为KIC或KC（平面应变或平面应力断裂韧度），下界为裂纹扩展门槛应力强度因子ΔKth。可以看出，在第I阶段，随应力强度因子幅度的降低，裂纹扩展速率呈现迅速下降的趋势。ΔK为门槛值ΔKth时，裂纹扩展速率趋近于零。若ΔK<ΔKth，可以认为疲劳裂纹不会扩展。

裂纹扩展从第I阶段向第II阶段过渡时，裂纹沿着与最大拉应力相垂直的方向扩展，此时即进入了扩展的第II阶段（裂纹稳定扩展阶段）。在低周疲劳的情况下，或表面有缺口、应力集中较大的情况下，第I阶段可不出现，裂纹形核后直接进入扩展的第II阶段。第III阶段的裂纹扩展迅速增大而发生断裂。断裂的发生由KIC或KC控制。

研究表明，ΔK及最大应力强度因子Kmax较低时，其扩展速率由ΔK所单独决定，Kmax对疲劳裂纹的扩展基本上没有影响；当Kmax接近材料的断裂韧度，如Kmax≥（0.5～0.7）KC（或KIC），Kmax的作用相对增大，Paris公式往往低估了裂纹的扩展速率。此时的da/dN需要由ΔK和Kmax两个参量来描述。此外，对于KIC较低的脆性材料，KIC对裂纹扩展的第II阶段也有影响。为了反映Kmax、KIC和ΔK对疲劳裂纹扩展行为的影响，Forman提出了如下表达式[14]：

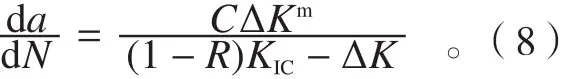
Forman公式不仅考虑了平均应力对裂纹扩展速率的影响，而且也反映了断裂韧度的影响。即KIC越高，da/dN值越小。这一点对构件的选材非常重要。

构件的疲劳裂纹扩展寿命可依据疲劳裂纹扩展速率公式估算得出。例如，考虑等幅循环载荷的作用下，利用Paris公式直接积分估算可得扩展寿命：

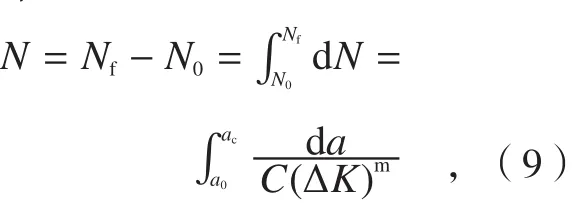
式中，N0为构件疲劳裂纹扩展至尺寸a0时的循环次数（若a0为构件的初始裂纹长度，则N0= 0），Nf为裂纹扩展至临界裂纹长度ac时的应力循环次数。

一般情况下，断裂力学方法用于评定构件中的裂纹状缺陷（如深度大于0.25mm的表面裂纹等）。对于焊接接头应力集中区而言，缺口效应本身就意味着存在原始缺陷，在疲劳载荷作用下很容易形成裂纹扩展。在疲劳裂纹扩展寿命分析中，初始裂纹尺寸的选取与材料类型有关。如铝合金的初始裂纹尺寸一般假设为a0= 0.01～0.05mm，钢材的初始裂纹尺寸一般假设为a0=0.1～0.5mm。表面裂纹则一般假设为深宽比a/c= 0.1～0.5的半椭圆裂纹。

Paris公式中的参数C和m值通过标准的试验方法获得。焊接接头各区域的组织性能各异，其中C和m值应分别试验测定。表面裂纹在板厚方向上的扩展和在板面方向上扩展的参数C和m将有所不同。一般而言，同种金属材料的不同组织状态下的C和m值只在一定范围内波动。例如，在da/dN和ΔK的单位分别为mm/周和N/mm3/2条件下，结构钢的C和m的取值范围为m=2.0～3.6，C=（0.9～3.0）×10-13。

焊接接头的力学性能不均匀性对疲劳裂纹扩展方向和扩展速率都有较大的影响[15]。因此，需在综合考虑焊缝力学失配效应的前提下进行焊接接头的疲劳裂纹扩展分析。一般来说，高匹配焊缝属于硬区，热影响区次之，母材为软区，源于焊缝区和热影响区的裂纹容易向母材一侧偏转。对于低匹配焊缝疲劳裂纹则局限在焊缝区扩展。焊缝力学失配对疲劳裂纹扩展的速率影响需要从裂纹扩展驱动力的变化等方面进行分析。

结束语

随着焊接结构疲劳研究的不断深入，疲劳设计与分析方法也得到发展。从疲劳持久极限和应力强度因子门槛值控制的无限寿命设计到利用S-N曲线、ε-N曲线和Miner理论进行的有限寿命设计，从裂纹萌生寿命评估到考虑疲劳裂纹扩展，综合控制初始缺陷尺寸、剩余强度及检查周期的损伤容限设计和耐久性经济寿命分析，疲劳强度分析与寿命预测的能力不断得到提升。对于具体焊接构件而言，不同的疲劳设计与分析方法之间并不是相互取代的关系，而是相互补充的，以满足不同工况的要求。

[1]RADAJ D, SONSINO C M, FRICKE W.Recent development in local concepts of fatigue assessment of welded joints[J]. International Journal of Fatigue, 2009,31(1):2-11.

[2]MADDOX S J. Review of fatigue assessment procedures for welded aluminium structures[J]. International Journal of Fatigue,2003,25(12):1359-1378.

[3]HOBBACHER A F. Recommendations for fatigue design of welded joints and components[M]. New York: Springer, 2008.

[4]张彦华. 焊接结构疲劳分析[M]. 北京: 化学工业出版社, 2013.

ZHANG Yanhua. Fatigue analysis of welded structure[M]. Beijing: Chemical Industry Press,2013.

[5]张彦华, 夏凡, 段小雪. 焊接结构合于使用评定技术[J]. 航空制造技术,2011(11):54-56.

ZHANG Yanhua, XIA Fan, DUAN Xiaoxue.Fitness for service assessment standards for welding structure[J]. Aeronautical Manufacturing Technology, 2011(11):54-56.

[6]陈科, 王峰. 结构有限寿命设计法—名义应力法[J]. 中国重型装备, 2010(2):1-3.

CHEN Ke, WANG Feng. Finite life design method—nominal stress method[J]. China Heavy Equipment, 2010(2):1-3.

[7]FRICKE W, KAHL A. Comparison of different structural stress approaches for fatigue assessment of welded ship structures[J]. Marine Structures, 2005,18(7/8):473-488.

[8]HOBBACHER A F. The new IIW recommendations for fatigue assessment of welded joints and components—A comprehensive code recently updated[J]. International Journal of Fatigue, 2009,31(1):50-58.

[9]MYUNG H K, SEONG M K, YOUNG N K, et al. A comparative study for the fatigue assessment of a ship structure by use of hot spot stress and structural stress approaches[J]. Ocean Engineering, 2009,36(14):1067-1072.

[10]BRUDER T, STORZEL K,BAUMGARTNER J, et al. Evaluation of nominal and local stress based approaches for the fatigue assessment of seam welds[J]. International Journal of Fatigue, 2012,34(1):86-102.

[11]FRICKE W. IIW recommendations for the fatigue assessment of welded structures by notch stress analysis: IIW-2006-09[M].Cambridge: Woodhead Publishing, 2012:2-41.

[12]MACDONALD K A. Fracture and fatigue of welded joints and structures[M].Cambridge: Woodhead Publishing, 2011.

[13]MARCOS Y S, REYNDERT C A,MAURICIO V D, et al. A brief discussion on (pure modeⅠ) fatigue crack growth rate data in 5HS weave fabric composites: evaluation of empirical relations[J]. International Journal of Fatigue,2015,84:97-103.

[14]FORMAN R G, KEAMY V E,ENGLE R M. Numerical analysis of crack propagation in cyclic loaded structures[J]. J. Basic Eng., 1967,89(3):459-463.

[15]张海泉, 张彦华, 李刘合, 等. 力学失配对电子束焊接接头疲劳裂纹扩展行为的影响[J].焊接学报, 2000, 21(13):40-43.

ZHANG Haiquan, ZHANG Yanhua, LI Liuhe, et al. Effect of mechanical mismatch on fatigue crack growth behavior of electron beam welded joints[J]. Transactions of the China Welding Institution, 2000, 21(13):40-43.