非线性振荡电路的一种新算法*

黄 偲

(中国能源建设集团广东省电力设计研究院网络信息部，广东 广州 510663)

非线性振荡电路的一种新算法*

黄 偲

(中国能源建设集团广东省电力设计研究院网络信息部，广东 广州 510663)

提出非线性振荡电路的一种新的计算方法，称之为响应频率迭代法。引进相位角作为自变函数，将非线性振荡电路的波形泛函表示成自变函数的余弦泛函，电路的响应频率即为自变函数对自变量的一阶导数，将电路非线性状态方程的求解归结为响应频率的确定，并用迭代法近似计算之；利用响应频率与相位角的微分关系，计算出反变换即时间与相位角的近似关系式，从而将非线性振荡电路的波形泛函随时间变化而变化的关系表示为以自变函数为参量的参数形式，突破摄动法的激励参数远小于1(即弱非线性)的限制，适用于强、弱非线性电路。具体分析了一类三极管振荡电路，取激励参数为0.8和1,经二次频率迭代，计算结果与数值积分法吻合良好，但摄动法已失效。

新算法；非线性振荡电路；非线性状态方程；波形泛函；响应频率迭代法

振荡电路，也叫信号发生器，是电子工程和技术中广泛应用的模拟电子电路，如大功率的振荡器、高频电源、低频电子技术实验、无线电广播电视信号的发送和接收、超声波探伤等测量、自动控制、通信和热处理等各种技术领域。

振荡电路的波形分析一般可归结为形如

(1)

这里，t是时间自变量。目前，线性电路分析法已较完善，而一般非线性电路尚无通用精确解法。常见的近似解法有数值积分法和解析法。数值积分法的特点是精度高，但是离散数值结果难以描述电路状态变量随时间的振荡变化，而且初值也难以确定。对弱非线性电路，传统近似解析法主要有摄动法、多尺度法、平均法和谐波平衡法等[1]。近年陆续出现其它相关研究工作[2-11]。

本文提出一种新的非线性振荡电路的近似分析方法，称之为响应频率迭代法。该法同时适用于强、弱非线性电路。本法引进相位角作为自变函数，将强非线性振荡电路的波形泛函直接表示为自变函数的余弦泛函，利用响应频率是相位角对时间的导数关系，计算出反变换即自变量t与自变函数φ的近似关系式，从而将强非线性电路的波形泛函随自变量变化而变化的关系表示为以自变函数为参变量的参数形式，将强非线性振荡电路的分析归结为电路的响应频率的确定，并以传统的迭代法近似求解之。作为应用，具体分析一类三极管反馈振荡电路，描画了电路的相轨线、时-程曲线和相-程曲线。计算结果及几何图形显示，本文的响应频率迭代法与数值积分的龙格-库塔法(精度可以任意接近精确解)吻合良好，精度明显优于摄动法。

1 响应频率迭代法

为了便于确定电路(1)的波形曲线，将方程(1)变形为一阶微分方程组

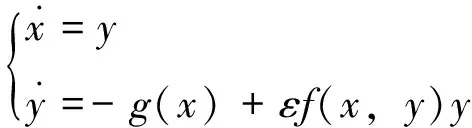
(2)

即将方程(1)在时程空间(x,t)上的问题，转换成相空间(x,y)上的分析。引进相位角φ=φ(t)作为自变函数，振荡电路(2)的波形假设为相位角φ余弦泛函：

(3)

自变量t与自变函数φ的变换关系式由微分关系式

(4)

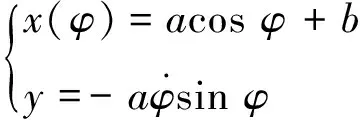
(5)

式(3)中，常量a和b是待定的电路振幅和偏心距。易知，当式(2)中的

即电路(2)是对称振子，则偏心距b=0。

式(4)改写为

上式对相位角φ由零开始积分，得时间t与相位角φ的关系式

(6)

式(6)中，t0=t(0)。于是，振荡电路的波形泛函x(φ(t))随自变量t的变化关系由如下的参数式确定

(7)

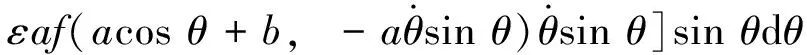
(8)

由式(8)可得振荡电路的响应频率为

(9)

分别取式(8)中的φ=2π和π, 得

(10)

(11)

一般地，式(10)和(11)是a和b的非线性代数方程，联立之是否有实数解、有几组实数解，分别对应于振荡电路是否发生振荡、出现几种波形，a和b分别为波形的振幅与偏心距。取式(6)中的φ=2π，t0=0，则电路的稳态波形的周期为

(12)

(13)

迭代法将第k+1次近似响应频率与第k次近似响应频率的关系即迭代格式表示为

(14)

振荡电路的n阶近似波形泛函相轨线为：

(15)

式(15)中，an和bn(n=1,2,…)由以下二式联立解出：

(16)

(17)

以上二式通常是an和bn非线性代数方程组，可由数值法近似求解。类似地，n阶近似的自变量tn(φ)和振荡周期Tn分别为：

(18)

于是，电路的n阶近似波形可写为如下参数形式

(19)

原则上，只要迭代次数k足够大，便可满足预定的计算精度。

关于波形的稳定性问题，可以式(19)确定数值积分为初值,进行数值模拟,并借助环域定量(Poincare′-Bendixson)进行判断[1]。

2 一类三极管反馈振荡电路分析

如图1所示的三极管反馈振荡电路(也称范德波振子)[1]，由于串联于集电极回路中的LC回路与基极回路之间互感M的存在，使回路产生自激振荡。

图1 三极管振荡电路Fig.1 Transistor oscillator circuit

设LC回路的电感L、电容C与电阻R中通过的电流分别为iL,iC,iR。设Ea为集电极回路中的电势，Va,Vg分别是集电极及基极电压，ia是集电极电流,M是基极回路与LC回路之间的互感系数。

由于基极电流很小，忽略不计。回路的状态方程为

经一系列的变量替换及数学处理，回路的状态方程可写为

(20)

式(20)即为著名的范德波方程，也称范德波振子。电路只有一个平衡点(0,0)。电路中，阻尼(电阻)显示非线性。将式(20)改写为一阶微分方程组

(21)

(22)

电路(21)周期振荡一次迭代的相-程曲线表达式为

取二次近似，并代入式(16)，得

(23)

方程(23)只有一个实根

(24)

将式(23)代入式(14)，得二次近似的响应频率

(25)

于是，电路(21)稳态振荡相轨线的二次近似表达式为

(26)

摄动法二次近似的振荡相轨线及响应频率如下[1]：

(27)

分别取ε=0.8和1时，数值法、本法及摄动法计算的相图比较分别见图2。

图2显示，ε=0.8时摄动法的误差十分显著，本法与数值法几乎重合；ε=1时摄动法与数值法已无可比性，而本法与数值法仍吻合良好。将式(25)记为

图2 电路(21)的三种解法比较Fig.2 Comparison of three methods for circuit (21)

这里，

(28)

(29)

将式(28)、(29)代入式(18)，并取a2≈2,ε=1,t0=0，得

1.057 6φ-0.181 1sinφcosφ-

就上述实施的条件和要求而言，无论在技术、硬件、经验、方法理论及相关法律法规等方面都具备了成熟的实施与应用的条件并有很多成功的案例可以借鉴和复用。

0.181 1sinφcosφ+0.505 2sin2φ+

0.358 8sin3φcosφ+0.053 9sin5φ·

0.094 7sin5φcos3φ+

0.007 0sin7φcos3φ+

0.007 8sin7φcos5φ-

0.244 4sin4φ+0.358 7sin6φ-

0.143 2sin8φ+0.050 0sin10φ

(30)

上式中，t2(φ)如式(30)。振子在时-程和相-程空间的波形曲线见图3，它们出现明显差异的原因是相空间与时程空间的周期各不同，分别是2π和Tn。

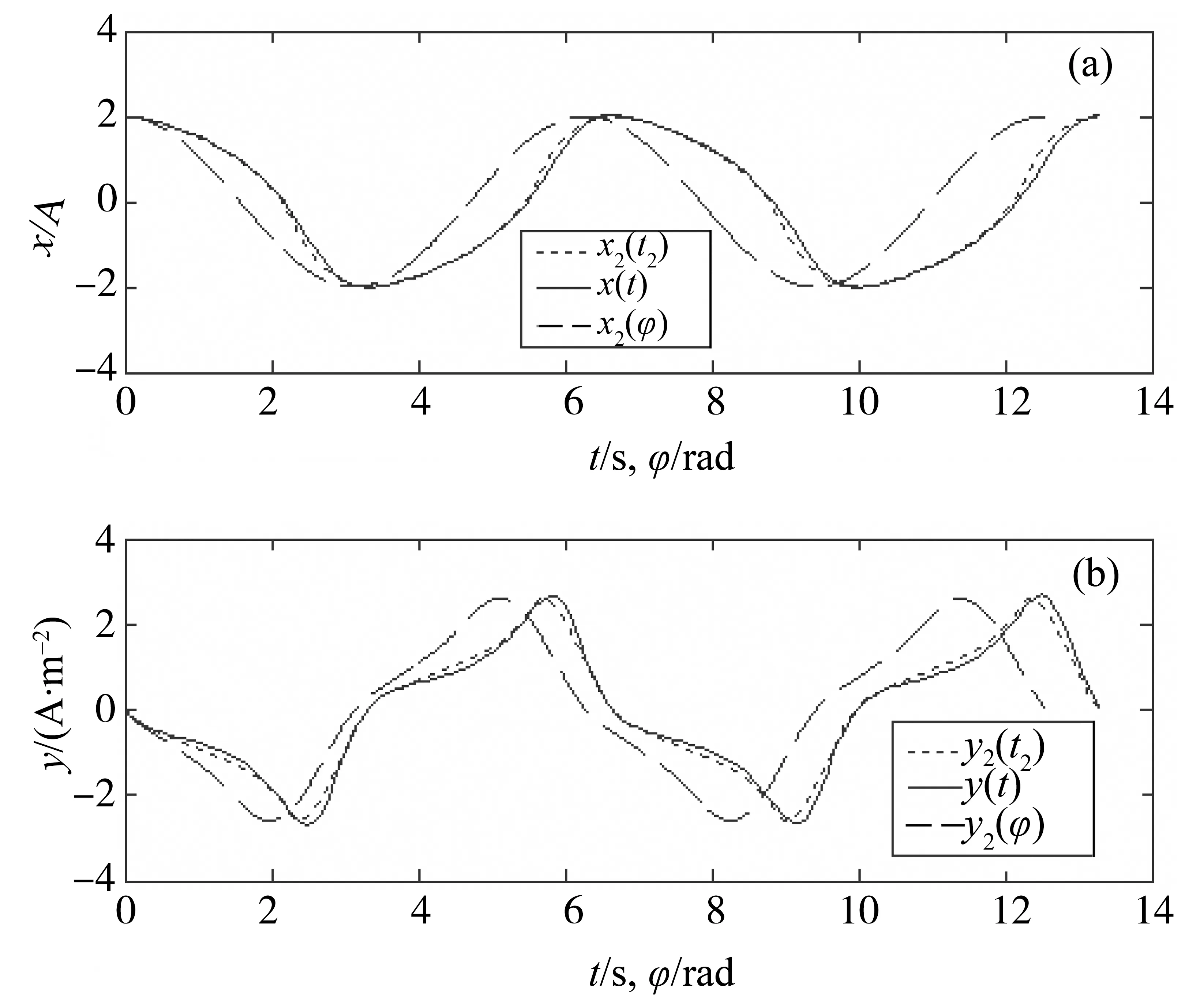
图3 电路(21)的三种解法时-程、相-程曲线比较Fig.3 Comparison of three methods of solution for time-path and phase-path curve of circuit (21)

图3中，x2(φ),y2(φ),x2(t2),y2(t2)是本文计算结果，x(t),y(t)是数值积分的结果。图形显示，本法的时-程曲线x=x2(t2)与数值法的时-程曲线x=x(t)吻合良好。

本文的方法(式(30) 中取φ=2π)、数值法和摄动法计算的极限环周期分别约为和6.655, 6.711。本法和摄动法与数值法的误差分别是0.01和0.056， 摄动法的误差是本法的5.6倍。

关于上述解答的稳定性，在相图的内外侧分别取点A(0.05,0)和B(3,3)作为数值积分的初值，其相轨线迅速收敛于解答(见图4(a))，由环域定理说明解答稳定。

为了进一步了解范德波振子(21)的特性，以调整参数ε=1 000进行r-k法数值计算，极限环相图如图4(b)。数值结果显示，该振子的稳定性很好，激励参数大至ε=1 000时，响应振幅仍然保持为无扰电路的固有振幅a=2不改变(响应频率随激励参数的增大而增大)。这对采用该电路的电子仪器(如示波器等)的工作状态为何如此 稳定，是很好的解释。

图4 电路(21)的极限环相图Fig.4 limit cycle phase diagram of Circuit (21)

顺便指出，非线性振荡电路的响应频率关于时间的变化是非线性的，如图5所示。电路(21) 当调整参数ε=1时等时间步长数值积分法的相点分布是很不均匀的(见图5)。经典摄动法将响应频率设定为与时间(或相位)无关的常量(如式(27))，与数值积分的结果明显不符，这是摄动法只适用于小激励参数即弱非线性电路(ε≪1)主要原因之一。本法不受小参数的限制，既适用于弱非线性、也适用于强非线性电路，且计算精度明显优于现有的分析方法。

图5 电路(21)等步长的相点分布Fig.5 Phase distribution of equal step length of circuit (21)

3 结 语

文中虽然没有一般性地讨论强非线性振荡电路(1)周期振荡的存在性、唯一性和稳定性等定性理论的基本问题，但对具体给定的电路，前二者由式(16)、(17)联立的非线性代数方程组实根的数目确定；后者可由本法与数值积分法相结合解决。具体做法是，以本法给出的近似解作为数值积分法的初值，由数值积分法描出的相轨线走向直接判别解答的稳定性。本法集强非线性电路的定性分析和定量计算于一身，对电路分析具有良好的理论意义实用价值。

致谢：衷心感谢导师余顺争教授和李宁教授对本工作的悉心指导。

[1] 邱关源. 现代电路理论[M]. 北京：高等教育出版社， 2006.

[2] 罗晓华，罗诗裕.三束储存与电子同步运动的动力学稳定性[J]. 中国科学(物理学，力学和天文学)，2014，44(2)：169-175.

[3] 袁常顺,王 俊,孙进平,等.一种幅度信息辅助多伯努利滤波算法[J].电子与信息学报，2016，38(2):464-471.

[4] 王金华，向红军，赵育林.一类非线性分数阶差分方程边值问题的存在性及Ulam稳定性[J].中山大学学报(自然科学版),2016,55(2):1-6.

[5] 黄偲，余顺争.非线性RLC电路的新解法及数值仿真[J].中山大学学报(自然科学版),2016,55(3): 83-88.

[6] 蔡烁，邝继顺，刘铁桥,等. 基于伯努利分布的逻辑电路可靠度计算方法[J].电子学报, 2015,43(11): 2292-2297.

[7] 张俊，罗大庸，孙妙平. 一种基于时滞区间不均分方法的变时延网络控制系统的新稳定性条件[J]. 电子学报，2016,44(1): 54-59.

[8]GIAOURISD,BANERJEES,IMRAYEDO,etal.Complexinteractionbetweentoriandonsetofthree-frequencyquasi-periodicityinacurrentmodecontrolledBoostconverter[J].IEEETransactiononCircuitsandSystemsI:RegularPapers, 2012, 59(1):207-214.

[9]YESOOHAV,KAVIPRIYAR,JOSHNTS,etal.AnalysisofchaosandbifurcationinDC-DCconverterusingmatlab[C]∥InternationalConferenceonCircuits,PowerandComputingTechnologies.Nagercoil:IEEE, 2013:481-487.

[10]RATHEEAA，PARTHASARATHYH.Perturbation-basedstochasticmodelingofnonlinearcircuits[J].CircuitsSystemsSignalProcess, 2012, 32(1): 123-141.

[11]FINGERL，UHLMANNH.EffectivecomputationofthepoincareMAPfortheanalysisofnonlineardynamiccircuits/systemsusingRunge-Kuttatriples[J].JournalofCircuitsSystem&Computers, 2011, 4(1) :93-98.

A new computation method of the nonlinear oscillation circuits

HUANGCai

(Network & Telecommunication Division, China Energy Construction Group Guangdong Electric Power Design & Research Institute,Guangzhou 510663, China)

A new calculation method of nonlinear oscillation circuit is presented and called as the response frequency alternation method. The phase angle is introduced as the independent functions. The waveform functional of the nonlinear oscillation circuit is shown as the cosine functional of the independent functions. The first derivative of the independent functions about the independent variable is meant by the response frequency of the circuit. The solution of the nonlinear state equation for the circuit is summed the determining of the response frequency for the circuit, and computed it with the alternation method. Using the differential relation of the response frequency between the phase angles, the approximate expression of the inverse transform for the independent variable is computed, and the expression of the variation for the state variable of the nonlinear oscillation circuit following with the time is shown as the parameter form of the independent functions. It is broken through the limit of the excitation parameters much less than 1 (i.e. weakly nonlinear) of the perturbation method and suitable for the strongly and weakly nonlinear circuit. A three-electrode oscillation circuit is discussed specifically with the excitation parameters of the 0.8 and 1, the calculation results are in good agreement with the numerical integral method after two times of iterative frequency, but the perturbation method is invalid.

new computation method; nonlinear oscillation circuit; nonlinear state equation; waveform functional; response frequency alternation method

10.13471/j.cnki.acta.snus.2016.06.015

2016-04-30

国家自然科学基金资助项目(11172334)

黄偲(1983年生)，男；研究方向：电子通信；E-mail:lendies@163.com

TN710

A

0529-6579(2016)06-0097-06