基于Split-Bregman方法的CT内重建算法研究

张丹丹，张煜林

(中北大学 信息探测与处理技术研究所,山西 太原 030051)



基于Split-Bregman方法的CT内重建算法研究

张丹丹，张煜林

(中北大学 信息探测与处理技术研究所,山西 太原 030051)

摘要：基于压缩感知(CS)理论，可证明只要感兴趣区域(ROI)可以表示为分段常数或多项式，CT内重建问题就可得到精确稳定的解.问题的关键是如何在截断投影数据的约束下最小化感兴趣区域的全变差(TV).与此同时，Split-Bregman方法在求解CT图像重建TV最小化方面引起了很大关注.本文基于CS理论将Split-Bregman方法用于一个分段常数成像模型的ROI重建，并与传统的SART和基于SART的软阈值算法(STF-SART)进行比较.最后经Shepp-Logan模型数值模拟表明：该方法适用、有效.

关键词：压缩感知；CT内重建；全变差最小化；Split-Bregman算法；分段常数成像模型

0引言

在CT领域，内部问题即ROI重建问题，其在处理大尺寸物体、减少辐射剂量、提高时间分辨率等方面都有很大潜力.在无约束条件下内部问题并没有独特的解决方案，基于常规CT理论并不能从截断的投影数据精确重建一个内部ROI.2007年，实验证明如果ROI内的一个子区域是已知的，内部问题可以得到精确稳定的解[1-3].然而，在实际应用中要获得一个子区域的精确信息非常困难，如心脏成像.基于压缩感知，2009年Yu和Wang进一步证实如果ROI是分段常数或多项式，精确内重建可以通过最小化ROI的TV实现[4-5].

离散梯度变换(DGT)已被广泛地用作稀疏算子，其L1范数被称为TV，相应的TV最小化方法也被用于基于CS的CT重建中，包括内部问题.TV最小化可以通过最速下降法或其他优化方法来实现.2010年，Yu和Wang应用软阈值滤波框架，通过构建DGT的一个伪逆变换实现了TV最小化[6].此外Split-Bregman算法在求解L1正则化问题方面引起了很大关注[7]，此方法对原来的L1正则化问题引入一个分裂变量后利用Bregman迭代求解[8].本文将Split-Bregman方法用于CT内部问题，并通过实验研究该算法的可行性.

1基于TV最小化的CT重建模型

基于TV最小化的CT图像重建问题可以表示为：

min‖f‖TV，s.t.‖Af-Y‖≤ε

(1)

其中A是投影矩阵，Y是投影数据，ε是测量误差，

对于上述问题,通常引入惩罚项将其转换为：

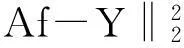
(2)

2Split-Bregman算法

式(2)表示的CT重建问题的Split-Bregman算法的主要步骤可以概括如下.首先引入两个新的变量将式(2)转换为：

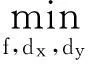
(3)

然后引入惩罚项，将(3)转换为：

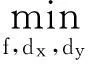
(4)

(4)可由Bregman迭代求解：

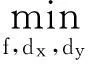
(5)

(6)

(7)

(5)可由交替方向乘子法(ADMM)交替迭代更新f和d：

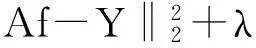
第一步可使用各种优化方法，考虑到CT重建矩阵A的特殊性，用最速下降法解决[9]：

fk+1=fk-αkgk

(8)

(9)

第二步可通过广义收缩公式求解：

(10)

(11)

基于Split-Bregman算法的CT重建的具体流程为：

S2：使用(8)执行梯度下降法；

S3：计算中间变量dx，dy，bx，by；

S4：转到S2，直到满足停止标准.

3实验设计及结果分析

本文采用一种改进的Shepp-Logan幻影图像进行仿真实验，幻影图像包括一系列分段常数椭圆，由256×256个像素组成，每个像素覆盖0.781 mm×0.781 mm的区域.扫描方式为圆轨迹扇束扫描，扫描半径为500 mm，探测器为包含320个探元的等角探测器，扇角为0.49 rad.为了评估算法的性能，实验在一次完整扫描中，等角采集不同数量的投影.为了进一步评估该算法的性能，实验通过舍弃正弦图两侧的80个探测器元件截断投影数据，使其只覆盖一个直径121.83 mm的圆形ROI，如图1(b)所示.

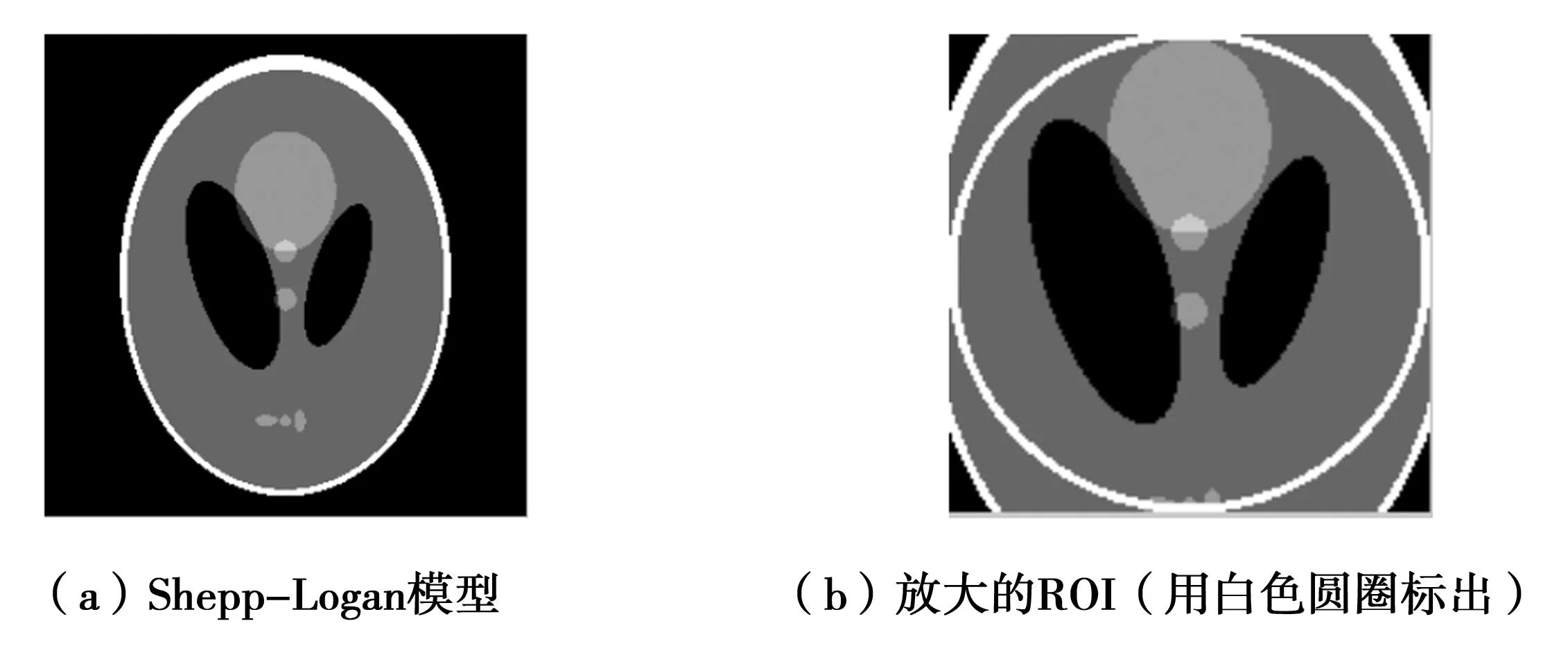
图1　改进的Shepp-Logan模型

实验在[0,2π)范围内均匀采集450个角度下的投影数据，使用Split-Bregman算法进行重建，并与传统的SART算法和STF-SART进行比较，迭代50次的重建结果如图2所示.为了定量地评估所提算法的性能，本文采用均方误差(MSE)作为评判标准.以迭代次数为横轴，三种算法重建图像的MSE为纵轴，画出的坐标图如图3所示.可以看出，Split-Bregman算法在迭代初期就显示出很大的优越性，重建结果明显优于其余两种算法.且对于ROI重建，TV最小化算法的重建图像具有很高的精度.

图2　450个角度下三种算法迭代50次的重建结果

图3　三种算法重建图像的MSE变化

为了评估Split-Bregman算法在稀疏角度内部重建方面的可行性，实验在[0,2π)范围内均匀采集60个角度下的投影，经过50次迭代的重建结果如图4和表1所示.所得结论与450个视角的情况相似.

表1　60个角度下三种算法重建图像的MSE

图4　60个角度下三种算法迭代50次的重建结果

4结论

针对CT内重建问题，本文基于压缩感知理论提出了一种Split-Bregman迭代算法，并通过仿真实验与SART和STF-SART进行了比较.实验结果表明，对于ROI重建问题特别是稀疏角度的情况，TV正则化(STF和Split-Bregman)算法明显优于传统的SART算法，且Split-Bregman算法在收敛速度和重建图像质量方面又优于STF-SART算法.后续研究工作将基于GPU或者使

用有序子集方法等对Split-Bregman算法进行加速.

参考文献：

[1]Ye Y,Yu H,Wang G.Exact Interior Reconstruction with Cone-Beam CT[J].Int.J.Biomed.Imaging, vol.2007, p.e10693, Jan.2008.

[2]Ye Y, Yu H, Wei Y, et al.A general local reconstruction approach based on a truncated Hilbert transform[J].Journal of Biomedical Imaging, 2007(1): 2-2.

[3]Ye Y, Yu H, Wang G.Exact interior reconstruction from truncated limited-angle projection data[J].Journal of Biomedical Imaging, 2008: 5.

[4]Yu H, Wang G.Compressed sensing based interior tomography[J].Physics in medicine and biology, 2009, 54(9): 2791.

[5]Yang J, Yu H, Jiang M, et al.High-order total variation minimization for interior tomography[J].Inverse Problems, 2010, 26(3): 035013.

[6]Yu H, Wang G.A soft-threshold filtering approach for reconstruction from a limited number of projections[J].Physics in medicine and biology, 2010, 55(13): 3905.

[7]Goldstein T, Osher S.The split Bregman method for L1-regularized problems[J].SIAM Journal on Imaging Sciences, 2009, 2(2): 323-343.

[8]Yin W, Osher S, Goldfarb D, et al.Bregman iterative algorithms for /ell_1-minimization with applications to compressed sensing[J].SIAM Journal on Imaging Sciences, 2008, 1(1): 143-168.

[9]Cai J F, Osher S, Shen Z.Linearized Bregman iterations for compressed sensing[J].Mathematics of Computation, 2009, 78(267): 1515-1536.

[责任编辑：王军]

Study on Split-Bregman algorithm for CT internal reconstruction

ZHANG Dandan，ZHANG Yulin

(Institute of Signal Capturing Processing Technology, North University of China,Taiyuan 030051, China)

Abstract:Based on Compressive Sensing (CS) theory, it can be proved that internal reconstruction of CT can get an accurate and stable solution as long as the region of interest (ROI) can be expressed as piecewise constant or polynomial.The key problem is how to minimize the total variation (TV) of region of interest under the constraint of the truncated projections.Meanwhile Split-Bregman method has caused great concern in solving the TV minimization problem for CT image reconstruction.In this paper, we apply the Split-Bregman approach to reconstruct an ROI for the CS-based interior tomography assuming a piecewise constant imaging model, and comparing with the traditional SART algorithms and soft thresholding algorithm based on SART (STF-SART).Finally Shepp-Logan model is applied as a test model to the simulation experiment, and the results shows that: this method is suitable and effective.

Key words:compressive sensing; Interior tomography; total variation minimization; Split-Bregman algorithm; piecewise constant imaging model.

中图分类号：TP391.1

文献标识码：A

文章编号：1672-3600(2016)06-0026-04

作者简介:张丹丹(1991-)，女，山西临县人，中北大学硕士研究生，主要从事图像重建研究.

收稿日期：2015-10-20