RV减速器静态回差分析及误差分配研究

赵海鸣，王　猛，张林林，李豪武，张怀亮

(1. 中南大学机电工程学院，长沙 410083；2. 中南大学高性能复杂制造国家重点实验室，长沙 410083)



RV减速器静态回差分析及误差分配研究

赵海鸣1, 2，王猛1，张林林1，李豪武1，张怀亮1, 2

(1. 中南大学机电工程学院，长沙 410083；2. 中南大学高性能复杂制造国家重点实验室，长沙 410083)

摘 要：以旋转矢量(rotate vector，RV)减速器为研究对象，分析了RV减速器静态回差的影响因素，建立了矩阵形式的静态回差分析数学模型，并推导出了针齿中心圆半径误差等15项误差的误差分配数学模型．以CSRV-160E-171型减速器为实例进行了误差分配计算，并基于误差分配结果进行PROE三维建模，建立了包含15项误差的虚拟样机模型1、模型2以分别模拟静态回差上、下限．建立了基于ADAMS的RV减速器回差仿真分析模型，提出了静态回差测试方案．仿真得出回差值为0.18′～1.19′，与设计值相似．仿真结果证明了误差分配数学模型的正确性．关键词：RV减速器；静态回差；误差分配；ADAMS回差仿真

旋转矢量(rotate vector，RV)传动是从摆线针轮传动的基础上发展而来的．由于其具有三大(传动比范围大、承载能力大、刚度大)、二高(运动精度高、传动效率高)和二小(体积小、回差小)的特点，被广泛应用于工业机械手臂关节、高精度数控机床等自动化设备领域．

回差是指输入轴反转时，输出轴在运动上滞后于输入轴的现象．由于零件加工、装配误差及负载和温度变化的存在，回差是不可避免的．回差分为静态回差和动态回差，前者只考虑零件加工、装配误差，后者还需要考虑负载和温度的变化．

最早有美国学者Blanche等[1]和Yang等[2]基于单级单摆线采用纯几何的方法推导了零件加工装配误差及间隙对输出轴的传动精度影响．其后日本学者日高照晃等[3]和石田武等[4-5]基于质量弹簧等价模型建立了两级、三曲柄、双摆线的精度分析模型，推导了零件加工装配误差单独及综合对输出轴的传动精度影响．近年来，国内许多学者也进行了一些相关精度与仿真研究，但大多是减速器单向传动精度研究[6-8]，只有少数学者对回差进行了从零件误差到回差的研究[9-10]．实际设计中，需要由给出的设计参数求出各零件的加工误差．本文以静态回差为研究对象，在分析回差影响因素的基础上，建立由回差设计要求到零件误差的误差分配数学模型，并基于ADAMS动力学仿真软件进行回差仿真研究．

1 减速器回差分析数学模型的建立

RV减速器属于2K-V型封闭差动轮系，由第1级渐开线齿轮传动和第2级摆线针轮行星传动构成．理论上输入轴反转后输出轴应该立即反转，但由于齿轮啮合侧隙及各零件的加工装配误差的存在和润滑要求，使输出轴有一个滞后量．本文在前人研究的基础上，按照误差均值和公差的形式建立了矩阵形式的回差分析数学模型，以方便MATLAB编程计算．

1.1 第1级渐开线传动回差分析模型

在第1级渐开线齿轮传动中，影响回差的因素主要有公法线平均长度偏差引起的齿轮侧隙、中心距误差引起的齿轮侧隙和行星轮齿圈径向圆跳动引起的齿轮侧隙[11]．

将文献[11]中的公法线平均长度偏差引起的回差公式总结归纳成矩阵的形式，可得到公法线长度平均偏差引起回差数学模型为

式中：i为减速器传动比；r1为渐开线中心轮分度圆半径；α为渐开线齿轮传动压力角；EWa为公法线平均长度上偏差；EWi为公法线平均长度下偏差；为公法线平均长度偏差引起的回差均值；为公法线平均长度偏差引起的回差的公差．

中心距误差ΔFa、齿轮齿圈径向圆跳动误差ΔFr引起的侧隙符合标准正态分布，故它们引起的回差均值为零[11]．

将文献[11]中的中心距误差及齿轮齿圈径向圆跳动误差总结归纳成矩阵的形式，可得到回差公差数学分析模型为式中：Kα为换算系数；α′为渐开线齿轮传动的啮合角；TΔFa为中心距误差的公差；TΔFr为齿轮齿圈径向误差的公差；为中心距误差引起回差的公差；为齿轮齿圈径向误差引起回差的公差．

第1级传动引起回差的均值

第1级传动引起回差的公差

1.2 第2级传动回差分析模型

第2级摆线针轮传动的零件误差对输出轴回差有直接的影响．在本级传动中，影响回差的主要因素有：摆线轮等距、移距修形及相关修形误差引起的啮合间隙；针齿中心圆半径误差、针齿销半径误差、针齿销孔圆周位置度及针齿销孔配合间隙引起的侧隙；摆线轮齿圈径向误差及周节累积误差引起的侧隙；转臂轴承游隙引起的侧隙；偏心距误差引起的侧隙．由等距修形与移距修形引起的回差[11]为

式中：a为偏心距；zc为摆线轮齿数；K1为短幅系数；为等距修形量；Δrp为移距修形量．

令

式中rp为针齿壳半径．

将文献[11]中的第2级传动各回差影响因素总结归纳成矩阵的形式，可得到其余部分回差分析模型为式中：A为回差分析系数矩阵；δ为误差均值列向量；Tδ为误差公差列向量；为误差引起的回差均值列向量；为误差引起的回差公差列向量；其余参数见表1.

表1　误差参数说明Tab.1 Illustration of error parameter

第2级传动引起回差的均值

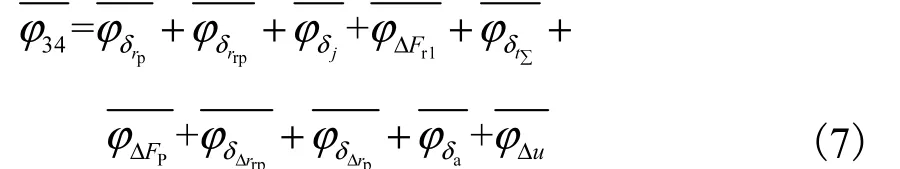
第2级传动引起回差的公差

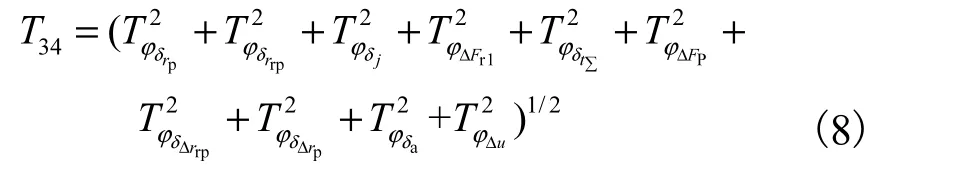
2 减速器回差影响因素误差分配数学模型

实际设计中往往是给出减速器回差的设计要求，通过合理分配求出减速器回差影响因素的误差．因此为缩短产品设计周期、提高设计效率，建立了减速器回差影响因素的误差分配数学模型．首先通过车间及市场调研，根据零件的加工工艺难度、加工成本及加工效率，将回差值合理地分配到各回差影响因素中；然后通过所建立的误差分配模型求出各因素的误差值．

2.1 第1级渐开线传动误差分配模型

对式(1)的系数矩阵求逆，得到渐开线传动公法线长度平均偏差误差分配数学模型为

对式(2)的系数矩阵求逆，得到中心距误差ΔFa、齿轮齿圈径向误差ΔFr的误差公差分配数学模型为

2.2 第2级传动误差分配模型

给定第2级回差均值、公差要求及其他基本参数，去掉等距加移距修形引起的回差，进行回差分配．对式(6)系数矩阵求逆得到第2级误差分配数学模型为

式(9)～式(11)即为RV减速器回差影响因素的误差分配数学模型．基于上述数学模型，通过MATLAB编程，即可实现从回差设计参数求解各项目误差的目的．由于该方法不需要像传统方法那样反复调整加工误差，因此大大缩短了RV减速器的产品设计周期和设计效率．

3 基于ADAMS的RV减速器回差仿真

为验证所建立的误差分配模型的正确性，采用ADAMS动力学仿真软件CONTACT中的基于IMPACT函数接触的方法，进行了基于ADAMS的回差仿真研究，并根据所得结果制定了回差测试方案．

3.1 影响回差的各误差项目等效处理

进行ADAMS回差仿真前，基于PROE三维建模软件进行虚拟样机1和样机2建模，以分别模拟回差上、下限．由于PROE仅具有建立标准模型的功能，故需要对各误差项目进行等效简化处理，以反映到标准模型中．对于尺寸公差及配合间隙，将零件标准尺寸与能够导致回差增大的极限偏差之和作为样机1的建模尺寸；将零件标准尺寸与能够促使回差减小的极限偏差之和作为样机2的建模尺寸．对于行星轮齿圈径向圆跳动，为检测到其引起的最大最小回差，用行星轮中心花键孔偏移ΔFr1来近似代替作为样机1和样机2的建模尺寸．对于摆线轮周节累积误差，因为周节间距的偏差使回差增大，故用沿摆线轮齿廓偏移ΔFP来近似代替作为样机1的建模尺寸，样机2不偏移．对于针齿销孔圆周位置度误差，因为针齿销孔沿径向存在向外的位置偏差而使回差增大反之使回差减小，故将针齿销孔中心沿径向向外偏移tδ∑进行样机1的建模尺寸，沿径向向内偏移tδ∑进行样机2的建模尺寸．

3.2 回差测试方案制定及回差仿真关键参数设置

回差是输入轴反转、输出轴在运动上滞后于输入轴的现象，笔者测试了输出轴转动1周减速器回差的变化情况．为实现输入轴不断正反转且正转角度大于反转角度，同时考虑换向的平稳，向输入轴添加转速为V＝a sin(Bt)＋C形式的正弦函数．本文采用式(12)对输出轴转动1周进行n次回差进行测试．

将PROE所建虚拟样机1和样机2保存副本为X_T格式导入ADAMS中，设置仿真环境，定义零件质量属性，添加约束、电机、接触及输出轴摩擦力．

为了能够准确地检测到减速器零件之间的侧隙，减小输出转速的波动量，添加CONTACT时采用IMPACT接触类型，将阻尼系数设为150．考虑到本文所检测侧隙为10-3数量级的，将接触穿透值设为10-4．在输出轴转动副上添加摩擦力以防止电机减速时，从动件由于惯性的作用导致零件之间侧隙减小甚至消除．通过理论计算输入轴反转到输出轴开始反转时间大约为0.005,s，考虑到ADAMS 1次仿真仅能计算10,000步，否则会因数据量大而导致系统异常，故仿真时间设为10,s，步长为0.001,s．为提高仿真精度，在进行仿真时采用GSTIFF刚性积分器和SI1积分格式进行求解计算．

4 实例

以CSRV-160E-171型减速器为例，给定关于回差方面的设计参数为0.2′～1.0′，回差均值为0.6，回差公差0.8．按照文献[11]中的经验数据，将回差均值和公差按比例分成3部分，并带入本文所建立的回差分配数学模型(式(9)～式(11))，运用MATLAB进行影响回差相关因素的误差分配计算，得出误差分配结果，如表2所示．由此建立了考虑各误差项目的虚拟样机1和样机2，进行ADAMS回差仿真以验证误差分配模型的正确性．样机1、样机2的各误差参数如表3所示．

按照以上参数进行样机建模，导入ADAMS中定义零件质量属性，添加约束和力接触，建立如图1所示的回差仿真模型．添加电机使输入轴转速为v＝15,390°,/s，输出轴转速波动小，平均转速为89.322,4°,/s，与理论值90°,/s相差0.7％,．说明该模型正确可靠．

表2　误差分配结果Tab.2 Results of error distribution

表3　样机1和样机2的误差参数Tab.3 Errors parameters of prototype 1 and 2 mm

图1　RV减速器回差仿真模型Fig.1 Backlash simulation model of RV reducer

添加电机使输入轴转速为v＝9,195,sin(30,t)＋6,195，设置参数进行仿真．图2为输入轴转速(以2个周期为例)，图3为样机1的输出轴转速，图4为样机2的输出轴转速，图5为输入轴转角，图6为样机1的输出轴转角，图7为样机2的输出轴转角．从图2中提取tj时间点，从图3、4中提取tj′，并从图5中求出代入式(12)中求出输出轴转1圈测得的95个点的回差值．绘出样机1和样机2回差值随输出轴角度的变化值，如图8所示．

图2　输入轴转速Fig.2 Input shaft angular velocity

图3　样机1输出轴转速Fig.3 Output shaft angular velocity of prototype 1

图4　样机2输出轴转速Fig.4 Output shaft angular velocity of prototype 2

图5　输入轴转角Fig.5 Input shaft angle

图6　样机1输出轴转角Fig.6 Output shaft angle of prototype 1

图7　样机2输出轴转角Fig.7 Output shaft angle of prototype 2

由图8可知样机1和样机2回差值呈周期性上下波动，这是由摆线轮齿圈径向圆跳动引起的．通过仿真得出的减速器回差值为0.18′～1.19′，与设计值0.2′～1.0′相差不大．仿真结果验证了RV减速器回差分配模型的正确性．

图8　样机1和2回差值Fig.8 Backlash of prototypes 1 and 2

5 结论

(1)建立了矩阵形式的静态回差分析模型，并由此推导了与静态回差有关的误差项目的误差分配数学模型．该模型提供了从设计要求到具体零件加工、装配误差的定量数学工具．利用MATLAB实现了快速计算与回差有关项目的误差值．

(2)提出了有关误差项目等效处理并反映到PROE所建模型中的方法，建立了基于ADAMS的RV减速器回差仿真分析模型，叙述了各关键仿真参数的确定方法及回差测试方案．通过仿真得出的减速器回差为0.18′～1.19′，近似于设计值0.2′～1.0′．该模型验证了误差分配数学模型的正确性．同时也为进一步进行RV减速器加工提供了理论支持．

参考文献：

［1］Blanche J G，Yang D C H. Cycloid drives with machining tolerances[J]. Journal of Mechanical Design，1989，111(3)：337-344.

［2］Yang D C H，Blanche J G. Design and application guidelines for cycloid drives with machining tolerances[J]. Mechanism and Machine Theory，1990，25(5)：487-501.

［3］日高照晃，王宏猷，石田武，など. サィクロィド齿车を用ぃたK-H-V?星齿车装置の回传达误差に関する研究(第1 报，解析方法)[J]. 日本耭械学会论文集：C编，1994，60(570)：645-653. Hidaka Teruaki，Wang Hongyou，Ishida Takeshi，et al. Rotational transmission error of K-H-V planetary gears with cycloid gear(1st report，analytical method of the rotational transmission error)[J]. JSME International Journal：Series C，1994，60(570)：645-653(in Japanese).

［4］石田武，王宏猷，日高照晃，など. 齒サイクロイド車を用ぃた K-H-V 遊齒車形星装置の回转传达误差に开する研究(第 2 报，各种加工误差、组立误差が回转传达误差に及ほす影响)[J]. 耭日本械学会论文集：C编，1994，60(578)：3510-3517. Ishida Takeshi，Wang Hongyou，Hidaka Teruaki，et al. Rotational transmission error of K-H-V planetary gears with cycloid gear(2nd report，effects of manufacturing and assembly errors on rotational transmission error)[J]. JSME International Journal：Series C，1994，60(578)：3510-3517(in Japanese).

［5］石田武，王宏猷，日高照晃，など. 齒サイクロイド車を用ぃた K-H-V 遊齒車形星装置の回转传达误差に开する研究(第3種报，各误差にほる相互影响)[J]. 耭日本械学会论文集：C编，1994，60(578)：3518-3525. Ishida Takeshi，Wang Hongyou，Hidaka Teruaki，et al. Rotational transmission error of K-H-V planetary gearswith cycloid gear(3rd report，mutual effects of errors of the elements on the rotational transmission error)[J]. JSME International Journal：Series C，1994，60(578)：3518-3525(in Japanese).

［6］朱 斌，秦 伟，孙 伟，等. 2K_V型摆线针轮减速器的动态回转传动误差分析[J]. 机械传动，2011，35(4)：12-15. Zhu Bin，Qin Wei，Sun Wei，et al. Dynamic revolution and transmission error analysis of 2K-V cycloidal pin planetary gear speed reducer[J]. Journal of Mechanical Transmission，2011，35(4)：12-15(in Chinese).

［7］杨玉虎，张 洁，许立新. RV传动机构精度分析[J].天津大学学报：自然科学与工程技术版，2013，46(7)：623-628. Yang Yuhu，Zhang Jie，Xu Lixin. Precision analysis of RV transmission mechanism[J]. Journal of Tianjin University：Science and Technology，2013，46(7)：623-628(in Chinese).

［8］李充宁，刘继岩，孙 涛. 2K_V型行星传动中摆线针轮啮合的传动精度研究[J]. 机械工程学报，2001，37(4)：62-65. Li Chongning，Liu Jiyan，Sun Tao. Study on transmission precision of cycloidal pin gear in 2K-V planetary drives[J]. Chinese Journal of Mechanical Engineering，2001，37(4)：62-65(in Chinese).

［9］吴俊飞，李魁贤，王庆华，等. 机器人用变厚齿轮RV减速器回差分析与计算[J]. 机械设计，2000(3)：24-28. Wu Junfei，Li Kuixian，Wang Qinghua，et al. The backlash analysis and calculation on bevoloid gear RV reducer used in robot[J]. Mechanical Design，2000 (3)：24-28(in Chinese).

［10］李充宁，蔡 胜，杨保占. 2K-V型摆线针轮减速机回差与刚度的试验研究[J]. 机械设计，2014，31(1)：33-36. Li Chongning，Cai Sheng，Yang Baozhan. Experimental research on lost motion and rigidity of type 2K-V cycloidal pin gear speed reducer[J]. Mechanical Design，2014，31(1)：33-36(in Chinese).

［11］张 展，张国瑞，张焕武，等. 实用齿轮设计计算手册[M]. 北京：机械工业出版社，2010. Zhang Zhan，Zhang Guorui，Zhang Huanwu，et al. The Calculation of Practical Handbook of Gear Design [M]. Beijing：Machinery Industry Press，2010(in Chinese).

（责任编辑：金顺爱，王晓燕）

网络出版时间：2014-11-26. 网络出版地址：http：//www.cnki.net/kcms/doi/10.11784/tdxbz201409029.html.

Static Backlash Analysis and Study on Error Distribution of RV Reducer

Zhao Haiming1,2，Wang Meng1，Zhang Linlin1，Li Haowu1，Zhang Huailiang1,2
(1. College of Mechanical and Electrical Engineering，Central South University，Changsha 410083，China；2．State Key Laboratory of High Performance Complex Manufacturing，Central South University，Changsha 410083，China)

Abstract：The rotate vector(RV)reducer was taken as a research object in this paper．The mathematical model of static backlash analysis was formulated in the form of matrix after analyzing the static backlash influencing factors of RV reducer．Then the mathematical model of error distribution was deduced which consisted of 15 errors including pin gear central circle radius error．The CSRV-160E-171 reducer was used as an example to distribute the error．The virtual prototype model 1 and model 2， which contained 15 errors，were built by PROE based on the result of the error distribution to simulate upper and lower limit values of static backlash．The backlash simulation analysis model of RV reducer was built based on ADAMS and the static backlash test scheme was put forward．The value of backlash simulation is 0.18′—1.19′，which is similar to the designed value．The results indicate that the error distribution mathematical model was correct.

Keywords：rotate vector(RV)reducer；static backlash；error distribution；backlash simulation based on ADAMS

通讯作者：王 猛，wangmengoffice@126.com.

作者简介：赵海鸣（1966— ），男，硕士，副教授，zhm0097@126.com.

基金项目：国家高技术研究发展计划(863计划)资助项目(2014AA041602)；湖南省科技计划资助项目(2013GK3007).

收稿日期：2014-09-10；修回日期：2014-11-17.

DOI:10.11784/tdxbz201409029

中图分类号：TH132

文献标志码：A

文章编号：0493-2137(2016)02-0164-07