基于CAE热分析的机床结构工作空间热误差建模

张大卫，杨金玉，高卫国，张伟展，刘　腾，牛文铁

(天津大学装备设计与制造技术天津市重点实验室，天津 300072)



基于CAE热分析的机床结构工作空间热误差建模

张大卫，杨金玉，高卫国，张伟展，刘腾，牛文铁

(天津大学装备设计与制造技术天津市重点实验室，天津 300072)

摘 要：在机床设计阶段，首先运用CAD软件建立几何模型；然后生成中间文件并导入CAE软件，进行机床结构热分析，通过后处理提取出运动轴导轨位置处的结构热变形误差；最后利用多体理论将结构热变形引起的单轴热误差转化为机床工作空间的热误差，进而预测由于机床结构热变形而引起的机床末端刀尖点-工件的相对位姿误差．仿真分析算例表明该方法具有可行性，对机床热平衡设计具有指导意义．

关键词：热分析；热误差；多体理论；工作空间；热平衡设计

Structural Thermal Error Modeling of Machine Tools in Working Space Based on CAE Thermal Analysis

Zhang Dawei，Yang Jinyu，Gao Weiguo，Zhang Weizhan，Liu Teng，Niu Wentie
(Tianjin Key Laboratory of Equipment Design and Manufacturing Technology，Tianjin University，Tianjin 300072，China)

Abstract：In the design phase of machine tools，firstly，geometric models were constructed based on CAD platform．Secondly，the intermediate files were generated and transferred to CAE platform，and structural thermal analysis was processed；structural thermal errors of machine tools along guideways of moving-axis were gained by post-processing．Lastly，thermal errors in working space caused by structural thermal deformation of machine tools were obtained from thermal errors of each single moving axis with the aid of multi-body theory，so that relative position and posture errors of tip-workpiece caused by structural thermal deformation of machine tools could be predicted．The simulation examples illustrate that this method is of feasibility and great value for thermal balance design of machine tools.

Keywords：thermal analysis；thermal error；multi-body theory；working space；thermal balance design

如何获得机床热误差并建立热误差模型，进而获得机床热变形对末端精度的影响规律是机床热平衡设计的关键问题之一．目前，建立热误差模型的方法包括多元线性回归分析模型[1-2]、人工神经网络模型[3-4]、支持向量机模型[5-6]和灰色模型[7]等，这些模型都能达到一定精度，但其共同点是均以实验法为基础．实验法需要花费大量的时间与费用，并且受实验条件限制，通常难以构建鲁棒性和普适性俱佳的模型；同时，实验法属于事后行为，即在机床制造完成后才能进行，而无法在设计阶段对机床的热特性进行预测和评价．

为了便于在设计阶段对机床的热特性进行合理的预测和评价，本文提出了以CAE热分析为基础的机床结构工作空间热误差建模方法．该方法能够通过CAE热分析快速地获得机床结构热变形误差，然后利用多体理论[8-9]预测由于机床结构热变形而引起的工作空间热误差，有利于实现机床的热平衡设计．

1 基本思想

基于CAE热分析的机床结构工作空间热误差建模方法的基本思想，是在机床设计阶段，将机床三维实体几何模型进行简化并导入CAE软件进行热-结构耦合分析，通过CAE后处理，获得机床结构导轨位置处的热变形误差；然后利用多体理论，计算出在理想条件和考虑机床结构热变形情况下的刀具姿态和刀具成形点在工件坐标系下的位置坐标，进而获得由于结构热变形所导致的机床工作空间热误差，从而在设计阶段，对机床结构热变形误差对末端精度的影响规律和影响程度进行评价，为机床热平衡设计奠定基础．基于CAE热分析的机床结构工作空间热误差建模方法的流程如图1所示．

图1　建模流程Fig.1 Flow chart of modeling

2 机床结构CAE热分析流程

2.1 CAD模型简化

在对机床进行CAE热分析前，应去掉分析模型中对分析结果无影响的细节特征．模型简化规则如下：①删除零件中较小的圆角和倒角，包括安装螺栓孔、螺钉孔、工艺孔、倒角和圆角等小特征；②删除滑座和工作台内部的齿轮传动机构、电机、轴承等，仅保留结构模型；③删除或修改尺寸小于50,mm的非关键凸台和凹槽特征．

2.2 CAE热分析

机床热结构分析涉及到热场、应力场两个物理场的相互作用，属于热-应力耦合场分析．对于热应力耦合场分析，ANSYS提供直接耦合法和间接耦合法．在两种耦合方法中，建立精确的模型是有限元热特性分析的关键所在．建立有限元模型包括3个重要内容，即分析工况选择、热载荷设置和热变形结果提取，而热载荷施加首先要进行机床热源分析和机床对流换热系数计算．

2.2.1 分析工况选择

机床工况分为快移工况和工作工况，且在两种工况下转台、溜板、主轴箱3大运动部件又位于不同位置．若每个运动件在自身运动方向上选取n种工况(n＞2)，组合可得n3种工况．

2.2.2 热载荷设置

机床的热源主要由两部分组成：内部热源和外部热源．内部热源主要是支撑轴承、丝杠螺母副、导轨滑块等相对运动产生的摩擦热和电机的电磁损耗生热，其生热量的计算采用相应的生热模型[10]获得；然后将生热量除以相应热源的面积或体积，进而求出热-结构仿真所需要加载的热载荷值，即热流密度或生热率；亦可以通过生热功能部件的热特性仿真分析获取其与机床结构结合面部位的温度场，然后直接将温度载荷施加于生热功能部件与结构的结合面部位．

2.2.3 机床对流换热系数设置

机床在生热的同时也和周围环境进行热交换．其热交换模式包括两类：自然对流和强迫对流．可以通过散热理论模型[11]计算出自然对流和强迫对流换热系数，将换热系数加载到有限元模型的对应位置，以模拟机床与环境的热交换条件．

2.2.4 热变形结果提取

为了分析结构热变形误差对末端精度的影响，需要在CAE后处理中获得x、y、z轴3个方向的误差，提取方法如下：取各大件上两条导轨上表面的4条棱作为提取路径，分别提取其变形量进而求出x、y、z轴3个方向的热误差．

3 基于多体理论的热误差建模

3.1 多体理论

多体理论由休斯敦[12]提出，已成功运用于机器人、并联机床等．天津大学刘又午将其应用于三轴、四轴机床误差分析，实现了多体运动学在机床精度分析与建模领域的应用．基于多体系统运动学理论的机床精度建模流程是首先根据机床的拓扑结构，用低序体阵列来描述机床各部件的关联关系，再用齐次特征矩阵来表示各部件之间的几何特征，计算刀具在工件子坐标系中的姿态以及刀具成形点在工件子坐标系中的位置坐标，从而完整地推导出有误差运动的运动学模型和机床在各种加工条件下的成形运动约束方程．

由于闭环系统均可转换成带有特定约束的开环系统，故本文以开环系统为研究对象．对于任意开环多体系统，拓扑结构示意如图2所示，图中R为惯性参考系，设为B0体，体1设为B1体，然后依次按增长数列为各个分支体编号．

图2　拓扑结构示意Fig.2 Sketch of topology

任意体Bj为系统中任意典型体，Bi是其相邻的低序体，定义

式中L为低序体算子.

体Bj为体Bi的相邻高序体，满足

且补充定义

根据以上定义，可得到图2开环多体系统的低序体阵列，如表1所示．

在惯性体B0和典型体Bi、Bj上分别建立与体固定联接的静坐标系Oxyz和动坐标系Oixiyizi、Ojxjyjzj，将典型体Bj相对于相邻低序体Bi的位置和姿态转化为坐标系Oixiyizi和Ojxjyjzj的相对位置和姿态．在坐标系Oixiyizi和Ojxjyjzj中，用齐次矩阵Tijp和Tijs来描述空间点在各坐标系中静止位置坐标变换和运动位置坐标变换．矩阵Tijp和矩阵Tijs包括理想特征矩阵和误差特征矩阵两种形式，分别用于描述理想静止、运动和实际静止、运动．

表1　低序体阵列Tab.1 Low body array form

通过对机床误差进行分析，依据多体系统运动变换矩阵，对于固定连接的两相邻体，得到体间理想静止特征矩阵和体间实际静止误差特征矩阵；对于相对运动的相邻体，不仅要得到上述两种特征矩阵，还要得到体间理想运动特征矩阵和体间实际运动误差特征矩阵，从而得到机床特征矩阵表．表中理想特征矩阵和实际误差特征矩阵的形式分别为

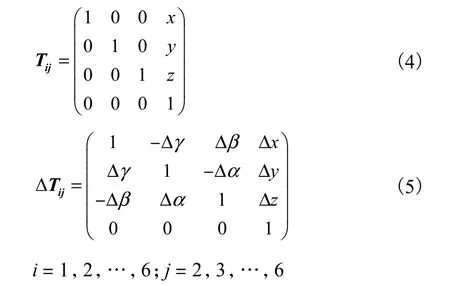
式中：x、y、z为j体坐标系相对i体坐标系沿x轴、y轴、z轴的移动位移；Δx、Δy、Δz为x、y、z向直线度误差；Δα为滚摆误差；Δβ为颠摆误差；Δγ为偏摆误差．

3.2 工作空间热误差

机床末端精度可以通过刀具成形点误差和刀具姿态空间误差两种方式来表达．

在坐标系Ojxjyjzj中，设工件所在坐标系为Owxwywzw，刀具所在坐标系为Otxtytzt，大地坐标系为Oxyz．

刀具成形点的运动状态、刀具的进刀角度即刀具姿态是成形运动的两个关键因素．成形点选取刀具上参与切削的点，即刀尖点；刀具的姿态选取固定在刀具上的矢量来描述，如刀具上刀柄至刀尖两点的矢量．设刀具成形点在刀具坐标系内的坐标为Pt，刀具姿态在刀具坐标系下的矢量为Vt，若要预测刀具误差，必须把坐标Pt和矢量Vt转换到工件坐标系中．

机床在理想情况下，刀具成形点Pt和矢量Vt在工件坐标系内的理想成形函数为

机床在有误差情况下，刀具成形点Pt和矢量Vt在工件坐标系内的实际成形函数为

式中方阵Tij、Tij(R)分别为机床相邻部件的体间实际位置特征矩阵和体间实际姿态特征矩阵．Tij是理想静止特征矩阵(Tijp)、有误差静止特征矩阵(ΔTijp)、理想运动特征矩阵(Tijs)和有误差运动特征矩阵(ΔTijs)4部分的乘积；Tij(R)是体间理想固定姿态特征矩阵(Tijp(R))、体间固定姿态误差特征矩阵(ΔTijp(R))、体间理想运动姿态特征矩阵(Tijs(R))和体间运动姿态误差特征矩阵(ΔTijs(R))4部分的乘积，即

实际刀具成形点与理想刀具成形点在工件坐标系下的误差、实际刀具矢量末端和理想刀具矢量末端的误差分别为

4 算例

以某卧式加工中心为例，说明如何将上述方法应用到机床的结构热变形分析与工作空间热误差建模中．

该加工中心由床身、工作台、立柱、溜板、滑台、主轴箱等结构件组成，采用框中框结构形式．x、y、z轴均采用双直线滚动导轨平行分布，滑台带动工作台在导轨上沿床身做z向运动；溜板在导轨上沿立柱做x向运动，主轴箱在导轨上沿溜板做y向运动，其简化后的三维CAD模型见图3．

图3　卧式加工中心结构示意Fig.3 Schematic diagram of horizontal machining center

将利用CAD模型生成的X_t中间文件导入到CAE软件里进行热应力耦合分析，采用的是间接耦合法，将热分析得到的节点温度作为载荷施加在后续的应力场分析中来实现耦合．

取9种工况：溜板、主轴箱不动，转台在z轴最前端、中间、最后端3个位置；转台、主轴箱不动，溜板在x轴最左端、中间、最右端3个位置；溜板、转台不动，主轴箱在y轴最上端、中间、最下端3个位置．其载荷施加见表2．

表2　载荷施加方式Tab.2 Load application form

将3导轨分别和大件粘接在一起，对机床进行热-结构耦合分析．以每根导轨的两条边为提取路径(以D1为例，见图4)，以其边上20个节点的变形量作为提取目标，画出位移曲线如图5～图8所示．

图4　提取路径Fig.4 Extraction path

图5　床身D1路径y向位移曲线Fig.5 y displacement curves of path D1 on bed

图6　立柱D1路径y向位移曲线Fig.6 y displacement curves of path D1 on column

分别以床身、溜板、立柱的变形曲线图为基础，通过作图分析求出3轴的误差见表3．以z轴误差为例：以转台前移0.3,m和转台后移0.3,m时床身重心坐标为已知点，过两点画直线，然后以转台位于中间位置时重心坐标为已知点，作上述直线的平行线，求出z轴的误差值．

根据卧式加工中心机床的实际结构、低序体序列描述方法和机床的约束，分别得出卧式加工中心机床的拓扑结构见图9(括号里的数字为坐标系原点坐标，单位为m)，低序体阵列见表4；然后根据平移运动特征矩阵和旋转运动特征矩阵的性质分别得出卧式加工中心各体之间的理想特征矩阵和误差特征矩阵(见表5)．

图7　立柱D1路径z向位移曲线Fig.7 z displacement curves of path D1 on column

图8　溜板D1路径z向位移曲线Fig.8 z displacement curves of path D1 on apron

表3　卧式加工中心的热误差Tab.3 Thermal error of horizontal machining center

0—大地(0，0，0)；1—床身(1.69，0，1.27)；2—滑座(1.69，0.87，2.38)；3—转台(1.69，0.87，2.38)；4—工件(1.690，1.460，2.355)；5—立柱(1.69，2.34，1.26)；6—溜板(1.69，2.34，1.64)；7—主轴箱(1.69，2.35，1.64)；8—主轴(1.69，2.35，1.64)；9—刀具(1.69，2.25，2.18)图9　卧式加工中心拓扑结构(单位：m)Fig.9 Topology of horizontal machining center(unit：m)

表4　卧式加工中心的低序体阵列Tab.4 Low body array of horizontal machining center

取刀尖点为刀具成形点，在刀具坐标系内的坐标为

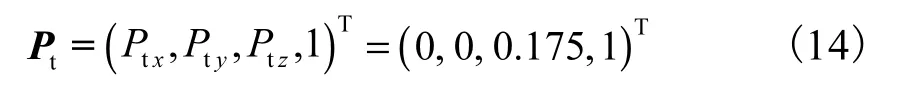
机床在理想情况下，刀具成形点Pt在工件坐标系内的理想成形函数为

表5　卧式加工中心特征矩阵Tab.5 Feature matrix of horizontal machining center

机床在有误差的情况下，刀具成形点和矢量在工件坐标系内的实际成形函数为

实际刀具成形点与理想刀具成形点在工件坐标系下的误差为

误差曲线见图10．

图10　误差曲线Fig.10 Error graph

从图10所示误差曲线可以看出：①机床末端x坐标误差由稳态误差、主轴箱移动距离y引起的放大误差两项组成，稳态误差和y引起的放大误差呈现抵消趋势，稳态误差为－2.65,µm，y的放大误差为4.7,µm/m；②机床末端y坐标误差由稳态误差、滑座移动距离z引起的放大误差组成，稳态误差和z引起的放大误差呈现叠加趋势，稳态误差为-3,µm，x的放大误差为1,µm/m；③机床末端z坐标误差由稳态误差、主轴箱移动距离y引起的放大误差组成，稳态误差和y引起的放大误差呈现叠加趋势，稳态误差为－2.98,µm，x的放大误差为1,µm/m．

5 结语

基于CAE热分析的机床工作空间热误差建模方法在机床结构CAE热分析基础上，利用多体理论，在机床设计阶段实现机床工作空间的热误差预测与评价，从而为机床热平衡设计与热主动控制奠定基础．

以一卧式加工中心为例，通过CAE热-结构耦合分析，得到了由于结构热变形引起的x、y、z导轨部位的4项直线度误差和4项转角误差，然后利用多体理论得到了由于结构热变形引起的机床工作空间的热误差分布．

参考文献：

［1］Yang Jianguo，Ren Yongqiang，Du Zhengchun. An application of real-time error compensation on an NC twin-spindle lathe[J]. Journal of Materials Processing Technology，2002，129(1)：474-479.

［2］Cui Liangyu，Gao Weiguo，Zhang Dawei，et al. Thermal error compensation for telescopic spindle of CNC machine tool cased on SIMENS 840D system [J]. Transactions of Tianjin University，2011，17(5)：340-343.

［3］Shen Jinhua，Yang Jianguo. Application of partial least squares neural network in thermal error modeling for CNC machine tool[J]. Key Engineering Materials，2009，39(2)：30-34.

［4］Yang S，Yuan J X，Ni J，et al. The improvement of thermal error modeling and compensation on machine tools by CMAC neural network[J]. International Journal of Machine Tools & Manufacture，1996，36(4)：527-537.

［5］Ramesh R，Mannan M A，Poo A N，et al. Thermal error measurement and modeling in machine tools (Part Ⅰ)：Influence of varying operating conditions [J]. International Journal of Machine Tools & Manufacture，2003，43(4)：391-404.

［6］Ramesh R，Mannan M A，Poo A N，et al. Thermal error measurement and modeling in machine tools (Part Ⅱ)：Hybrid Bayesian network-support vector machine model[J]. International Journal of Machine Tools & Manufacture，2003，43(4)：405-419.

［7］李永祥，杨建国. 灰色系统模型在机床热误差建模中的应用[J]. 中国机械工程，2007，17(23)：2439-2442. Li Yongxiang，Yang Jianguo. Application of grey system model to thermal error modeling on machine tools[J]. Chinese Journal of Mechanical Engineering，2007，17(23)：2439-2442(in Chinese).

［8］Huston R L，Passerello C E，Harlow M W. Dynamics of multirigid-body systems[J]. ASME Journal of Applied Mechanics，1978，45(4)：889-894.

［9］Huston R L，Passerello C E. Multibody structural dynamics including translation between the bodies [J]. Computers and Structures，1980，11：713-720. ［10］吕妍菲. 数控机床热特性分析计算及试验研究[D].大连：大连理工大学机械制造及其自动化学院，2012. Lü Yanfei. Thermal Characteristics Analysis and Test of Machining Center[D]. Dalian：School of Mechanical Manufacture and Automation，Dalian University of Technology，2012(in Chinese).

［11］Mian N S，Fletcher S，Longstaf A P，et al. Efficient thermal error prediction in a machine tool using finite element analysis[J]. Measurement Science and Technology，2011，22(8)：085107.

［12］休斯敦R L. 多体系统动力学[M]. 刘又午，译. 天津：天津大学出版社，1987. Houston R L. Multibody System Dynamics[M]. Liu Youwu，Trans. Tianjin：Tianjin University Press，1987(in Chinese).

（责任编辑：金顺爱）

网络出版时间：2015-06-09. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.n.20150609.1006.001.html.

通讯作者：高卫国，gaowg@tju.edu.cn.

作者简介：张大卫（1962— ），男，博士，教授，medzhang@tju.edu.cn.

基金项目：“高档数控机床与基础制造装备”科技重大专项资助项目(2013ZX04005-013).

收稿日期：2015-01-29；修回日期：2015-05-21.

DOI:10.11784/tdxbz201501079

中图分类号：TH123

文献标志码：A

文章编号：0493-2137(2016)02-0111-09