数学课堂中有效提问的时机

摘 要把握课堂提问的时机是实现有效提问的关键,它对学生思维的启动、展开和延续过程具有重要意义。在数学课堂上,教师有效提问包括复习中提问、情境中提问、困惑中提问、对话中提问、应用中提问、小结中提问等六个典型时机,它们分别对思维起着准备、启动、融合、引导、变迁和巩固作用。
关键词有效提问 提问时机 思维
评判教师的有效提问应以引起学生“积极思考”的状态和思维的品质为标准。“积极思考”是促进课堂有效教学行为发生的着力点,对推动教学进程发挥动力作用[1]。在数学课堂中,教师要善于引导学生进行积极思考,采取各种措施优化课堂提问,实现提问价值的最大化[2]。有效课堂提问的价值取向,从教学目标维度解读有助于发展学生的思维、彰显师生主体性;从教学过程维度解读,是预设与生成的辩证统一,是关注课堂对话的开展、追求卓越的动态发展过程[3];而从提问的时机与技巧维度解读,是教师技能与教学艺术的外在表现,是扩充数学课堂的知识广度、思想深度和智慧厚度,实施高效教学的必要诉求。教师把握课堂提问的时机是实现有效提问的关键,它对学生思维的启动、展开和延续过程具有重要意义。
一、复习中提问——思维的蓄势
上课伊始,教师经常要引导学生有针对性、有顺序地回顾已学内容。这是巩固所学、强化重点和集中学生注意力的做法,让新课在旧课基础上延续,复习起“承上”的作用。但对于一堂新课而言,复习只是起点,“承上”是为了“启下”,“温故”是为了“知新”。在复习的过程中,教师要抓住新课内容的联系点进行提问,为将学的重点或难点知识做好知识准备,为思维的开启架设桥梁。教师在复习中的提问点主要包括:前一节课中未解决的问题,前一节课的重点问题或疑难问题,与将学知识紧密相关可以衍生出的新问题。
案例1: 全国著名数学特级教师孙维刚在《一元一次方程的应用(5)》一节课的复习引入环节中,就精心设计并实施了课堂有效提问。孙老师首先引导学生复习列出一元一次方程解应用问题的一般方法,为后续研究具体的应用问题——行程问题奠定了重要基础。然后,孙老师提出了一个问题:我们应该怎么去思考和处理行程问题呢?看似难以回答的问题,经教师的启发使学生自然地联系到小学阶段熟悉的几个关于行程问题的关系式,并让学生领悟到“实践出真知”的哲理,学生认清了为什么要“先练后学”,为后边解决行程问题的思考蓄势,使得引入一元一次方程解决行程问题以及怎样列方程更为恰当变得水到渠成。
点评:孙老师的这个提问让学生站到了一定的思想高度,与奥苏贝尔的有意义学习理论暗合,其作用是既让学生把握住了已学内容的要点,又帮助学生找到了如何抓住新旧知识联系点的学习方法,更为研究新知识和展开新思维起到准备作用。
二、情境中提问——思维的激发
情境认知理论认为,任何数学知识都是与情境相关的,也就是说要将数学知识的教与学置于一个情境脉络之中,是知识本性所决定的[4]。因此,教师要常常将教学内容根植于教学情境之中,并在创设情境时提出一些有价值而蕴含一定思考力度的数学问题,以此激发学生的思维,产生认知驱力。
案例2 :在引进“相似”概念的时候,教师在黑板上画了一只“巨人的手”,再对学生说:“昨晚外星人访问我校,在黑板上留下了一个巨大的手印。今天晚上他还要来。你能为外星人设计大小合适的书、高矮合适的桌椅吗?”学生们用自己的手和巨人的手进行比较,得出“相似比”,然后把教科书、桌子、椅子按此比例放大,得到巨人使用物品的尺寸。
点评:这是荷兰数学教育家弗赖登塔尔设计的一个经典情境——“巨人的手”。该情境突出了“新奇”的特点,简单而富有创意。教师提问的成功之处在于既引发学生强烈的兴趣,产生有意注意,又将学生后续的“设计”活动与“相似”概念的初步认识巧妙地结合起来,激起求知的欲望,自然地诱发学生深层次思考。教师的提问对学生思维的产生发挥启动作用。
四、对话中提问——思维的碰撞
对话教学是以对话为精神的教学,是对话主体从各自的理解出发,以语言文字等为媒介、以沟通为方式、以意义的生成为实践旨趣,促进主体取得更大的视界融合的一种活动[6]。对话教学的过程是伴随问题的发现、提出、分析和解决的线索的,整个问题线索由师生共同来维持,即在教学中不断通过问题来引发思维的碰撞。但要实现思维碰撞的提问必须抓住提问的关键点,提问的关键点的类型通常包括对话中的生长点、衔接点、转折点、深化点、症结点等。
案例4 :沈茂宏老师在执教“圆的面积”一课时,善于以问题为驱动引导学生进行对话交流,师生在对话交流中积极思考,逐步实现“视界融合”[7]。
师:小明家的圆形餐桌要配一张软玻璃,他去装修店问好了价钱,工人师傅说,“你家圆桌尺寸多大?你回家量好后告诉我,我做好了送货上门”。小明回家后才发现自己粗心,没有问工人师傅量什么尺寸。同学们想一想,小明该量什么尺寸?(在对话的“生长点”提问)
生1:量直径。生2抢着说:不知道圆心,怎么量直径?量周长!用卷尺围着圆桌量一周就好了。
生1不服气地补充到:把桌面对折一下就知道直径了。
老师笑问生1:桌面怎么对折?(在对话的“衔接点”提问)生1恍然大悟,不好意思地坐下了。
生3解释说,用两个三角板和一把直尺,就可以量直径了。老师启发生3:尺子怎么摆放?(在对话的“深化点”提问)
生4插话说:把桌子竖起来,桌面贴着墙。老师追问生4:这样还需要两个三角板吗?(在对话的“转折点”提问)
有的同学顿悟,这个办法只需要一个三角板和一把直尺就可以量出直径。
生5举手,小心地试探:量直径这么麻烦,量半径行不行?(在对话的“转折点”提问)
生2反问生5:量半径怎么知道圆心在哪里?(在对话的“症结点”提问)还是我的办法好,量周长。
师:看来量周长还是比量直径简单。
生2很有成就感地坐下了。
最后,教师给予了点评,学生们最终明确了知道圆的半径、直径、周长中的一个量就能求其面积,反之知道圆的面积也能求圆的半径、直径和周长。
点评:在该片段中教师的参与并不多,但成功地以追问的方式激活了学生思考的共鸣点,促进了学生思维的迁移、深入和碰撞。此时,教师的提问让师生的思维不断发生碰撞,发挥了提问对思维的融合作用。
五、应用中提问——思维的延伸
教师在引导学生应用知识解决问题的过程中,要根据学生反馈情况抓住时机提问。如果教师只是引导学生“为应用而应用”或“为解题而解题”,那么数学应用的目的是难以实现的,或是难以充分挖掘题材的价值,取得教学的最大“效益”。反之,教师如果结合具体的题材对学生表现出的行为和状态进行密切关注和调控,并提出有针对性的问题,引导学生开展生成性学习,就能使学生巩固所学的新知识,矫正一些不好的做法,为学生积累解决问题的经验,充分调动学生创新意识,提升思维品质和实现思维的延伸。
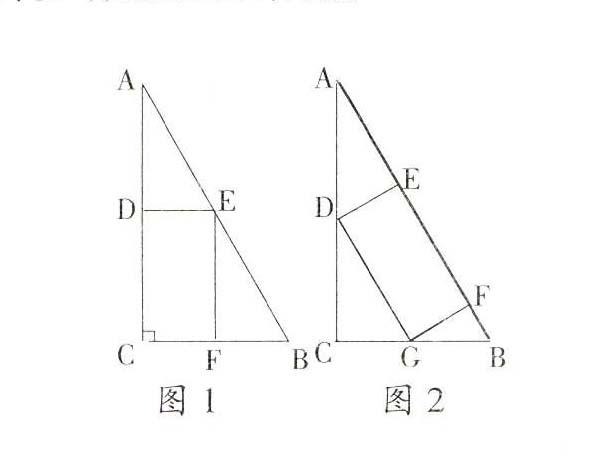
案例5:在学习“实际问题与二次函数”(人教版九年级(下))一节时,一位教师选择了教材上一道综合运用题让学生练习:一块三角形废料如图1所示,∠A=30°,∠C=90°,AB=12。用这块废料剪出一个长方形CDEF,其中,点D,E,F分别在AC,BC上。要使剪出的长方形面积最大,点E应选在何处?
这位教师在学生解出本题后给予了总结,然后向学生提问:“同学们,本题剪出的长方形的一边在BC边上,如果剪出的长方形一边在AB边上(如图2),那么又如何求解呢?又或是本题剪出的图形为正方形,情况又如何呢?”通过本题,该教师引导学生提出更多的变式问题,并结合几何画板探究出了许多有意思的结论。
点评:教师在学生应用所学知识解决问题的过程中提出问题,实施了生成性的变式教学,做到了知识的深化应用与思维的延伸。教师的提问使学生的思维在广度和深度上发生了变化,解决问题的思路和方法实现了正迁移,因此,教师的提问对思维的延伸发挥了变迁作用。
六、小结中提问——思维的强化
课堂小结是课堂的重要组成部分,对教学内容起画龙点睛、提炼升华、延展拓深的作用。但在实际教学中,许多教师对小结不够重视,往往匆忙应付就结束了,造成一节课“虎头蛇尾”。教师在小结中有针对性地提问,可以强化一些重要的方法、特定的某些策略或矫正一些错误的操作,使学生思维在头脑中形成完整而正确的图示。
案例6 :在北师版八年级(下)《相似多边形的性质(1)》一节课结束时,一位教师通过提问的方式引导学生进行小结[8]:
师:本节课,大家发现了相似三角形的什么规律?
生:相似三角形对应高线、中线、角平分线的比等于相似比;周长的比等于相似比;面积的比等于相似比的平方。
师:我们用什么知识发现这些结论的?
生:用相似三角形的有关知识。
师:大家认为还需要研究什么问题?
生:需要研究四边形、五边形以及n边形的对应周长与面积的比。
师:这些内容我们将在下一节课中集中进行讨论。
点评:这位教师的小结内容虽然短小,但却是一节课的点睛之笔。小结中既总结了本节的重点知识,检验了学生的掌握情况,贯通了知识间的关联,强化了思维的连贯性,使知识更系统化;又通过拓展性提问,反映出学生清晰的学习思路,凸显了发散性思维,为下一节内容做好铺垫。教师的提问对思维在头脑中产生的图示发挥了巩固作用。
参考文献
[1] 潘超,吴立宝.引导学生积极思考的六个触发点[J].中学数学教学参考(中旬),2013(9).
[2] 李鹏,傅赢芳.论数学课堂提问的误区与对策[J].数学教育学报,2013(4).
[3] 卢正芝,洪松舟.教师有效课堂提问:价值取向与标准构建[J].教育研究,2010(4).
[4] 谢明初.情境认知理论对数学教育的意义[J].教育研究,2009(8).
[5] 黄晓学.论思维生惑点与数学教学[J].数学教育学报,2007(2).
[6] 刘庆昌.对话教学初论[J].教育研究,2001(11).
[7] 马学斌,王叶红.老师三放三收,学生思维激荡[J].中学数学教学参考,2007(3).
[8] 石生民.初中数学课例点评[M].西安:陕西师范大学出版社,2008.【责任编辑 郭振玲】

