《中心对称图形
——平行四边形》错题汇集与解析
吴晓茹
《中心对称图形
——平行四边形》错题汇集与解析
吴晓茹
平行四边形相关知识是中考重要的考点之一,但在解决与平行四边形相关的问题时,由于考虑问题不全面或识图能力的限制,往往会出现各种错误,为帮助同学们更好地学习这部分内容,现对几种常见的错误类型解析如下.
例1平行四边形一个内角的角平分线把一条边分成长为3和4的两部分,求平行四边形的周长.
【错误解答】22.
【错因剖析】考虑问题不全面,只看到了分成两部分,但没有注意到,到底是哪部分为3,哪部分为4.
【正确解答】如图1,
∵四边形ABCD是平行四边形,
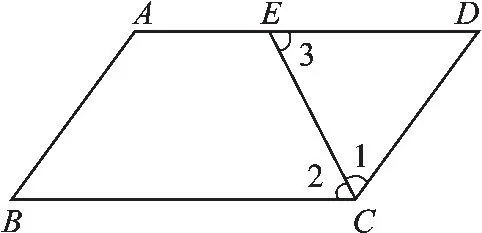
图1(1)
∴AD∥BC,
∴∠2=∠3,

图1(2)
∵CE是∠BCD的角平分线,
∴∠1=∠2,
∴∠1=∠3,
∴DE=DC.
当AE=3,DE=4时,如图1(1),平行四边形的周长为AB+BC+CD+AD=4+7+4+7=22,
当AE=4,DE=3时,如图1(2),平行四边形的周长为AB+BC+CD+AD=3+7+3+7=20.
【点评】分类讨论是初中数学中一种重要的思想,在解决几何问题时,自己多画画图,就能够在画图的过程中发现存在两种情况.
例2下列说法中正确的是().
A.一个角是直角,两条对角线相等的四边形是矩形
B.一组对边平行且有一个角是直角的四边形是矩形
C.一个角是直角且对角线互相平分的四边形是矩形
D.对角线互相垂直的平行四边形是矩形
【错误解答】B.
【错因剖析】B提供的两个条件都是判定矩形所必需的,但是这些条件对于判定直角梯形也成立.
【正确解答】C.
【点评】判定一个四边形是矩形分两种情况,第一种是在平行四边形的基础上判定该四边形是矩形,即只要再证出有一个角是直角或对角线相等;第二种是在四边形的基础上判定该四边形是矩形,可以直接证出有三个角都是直角或者运用转化的数学思想,先证明四边形为平行四边形,再进一步证明是矩形.
例3已知菱形ABCD中,对角线AC与BD相交于O,∠BAD=120°,AC=4,则该菱形的面积是().
C. 16D. 8
【错误解答】A.

【点评】我们在记忆一些计算公式时,应该多理解,并能够自己推导出这些公式.在理解的基础上记忆,就能避免这样的错误.
例4如图2,将矩形ABCD沿直线EF对折,点D恰好与BC边上的点H重合,∠GFP= 62°,那么∠EHF的度数等于_______.
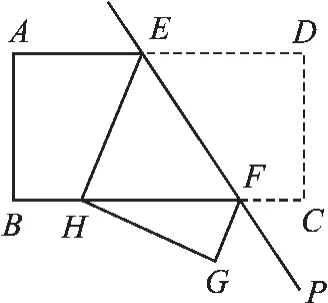
图2
【错误解答】62°.
【错因剖析】一部分学生不能准确理解图形变换前后到底可以得到哪些信息,于是看到什么数字就填写什么答案,完全是蒙的.
【正确解答】56°.
∵矩形ABCD沿直线EF对折,点D恰好与BC边上的点H重合,
∴HE∥FG,∠CFP=∠GFP=62°,
∴∠EHF=∠HFG=180°-∠CFP-∠GFP= 180°-62°-62°=56°.
【点评】一定要抓住翻折前后得到的图形是全等的(这题主要利用对应角相等),再利用平行线的性质即可正确算出结果.
例5若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是().
A.矩形
B.菱形
C.对角线相等的四边形
D.对角线互相垂直的四边形
【错误解答】B.
【错因剖析】顺次连接菱形四边的中点得到的确实是一个矩形,但是答案还不全面.
【正确解答】D.
如图3,由于E、F、G、H分别是AB、BC、CD、AD的中点,
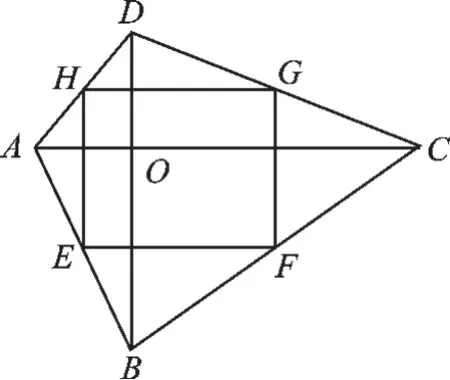
图3
根据三角形中位线定理得:
EH∥FG∥BD,EF∥AC∥HG,
∵四边形EFGH是矩形,即EF⊥FG,
∴AC⊥BD,
故选:D.
【点评】根据三角形中位线定理,我们可以证出任意一个四边形的中点四边形都是平行四边形,所得的平行四边形的边和原四边形的对角线有着相应的位置和数量关系,因此,若所得平行四边形是矩形,即邻边互相垂直,故原四边形的对角线必互相垂直;若所得平行四边形是菱形,即邻边相等,故原四边形的对角线必相等.
【综合点评】中心对称图形是中考命题的热点,涉及平行四边形和特殊的平行四边形的知识点较多,特别是平行四边形的性质和判定.所以我们在学习这一章的时候如果能结合图形理解掌握所学的知识,并灵活应用,融会贯通,相信所有同学都能有所收获.

