A new model in correlating and calculating the solid-liquid equilibrium of salt-water systems☆

Xianzhen Xu,Yangdong Hu,Lianying Wu,Xia Chen

College of Chemistry and Chemical Engineering,Ocean University of China,Qingdao,Shandong 266100,China

1.Introduction

Electrolyte solutions are encountered in many naturaland industrial processes.The activity coefficient model for electrolyte solutions is widely used in chemical engineering,geochemistry and other fields,such as seawater desalination,crystallization,corrosion studies,hydrometallurgical studies,and environmental application.So,the study for electrolyte solutions is an important research topic.

A number of activity coefficient models for concentrated electrolyte solutions have been developed for calculating the thermodynamic properties of electrolyte solutions for engineering applications.Some examples are the ElecNRTL model of Chenet al.[1-3],Pitzer's model[4],the OLI MSE model of Wanget al.[5,6],the Lu-Maurer model of Luet al.[7,8],These models combine local composition activity coefficient models(the short-range interactions)with the Debye-Hückel's law[9]or Modified Debye-Hückel's law(the long-range interactions).Thomsenet al.[10,11]and Xuet al.[12]studied vapor-liquid equilibrium(VLE),and the models can successfully correlate and predict VLE data in electrolyte solutions.These models mentioned above have been successfully used to calculate the thermodynamic properties of electrolyte solutions at high temperature and high concentrations.

However,describing the thermodynamic properties of electrolyte solutions using conventional thermodynamic models has been quite challenging.Modeling solid-liquid equilibrium for some multicomponent electrolyte solutions is still incomplete.For multicomponent electrolyte solutions,the complicated calculation and low accuracy are the major drawbacks of conventional model.Therefore,It is necessary to explore a new modelto accurately and simply describe the thermodynamic properties of electrolyte solutions.

2.Model Description

A Modified NRTL model[12]has been successfully proposed to correlate and predict VLE data for electrolyte solutions in our previous work.We obtained the final equation and tested this approach for water activity between 298.15 K and 415.85 K.In this work,a new model is proposed to calculate SLE data in electrolyte solutions.

2.1.Activity coefficient and the new reference

It is still assumed that the solute in the electrolyte solution exists as molecule like our previous work.The activity coefficientofsolute in this work is the same meaning as the mean ionic activity coefficient in other model.

In this work,It is assumed that the new reference state ofactivity coefficients in this model is the activity of soluteai(=mi× γi)→1 asmi→the solubility.The reference is meaningful only to SLE,not to the other situations.

Table 1Results of correlation for mixed electrolyte solutions

Because of the change of the activity coefficient's definition and the reference,it is not necessary to consider the situation ofmi→0.SLE literature data analysis is in the high concentration,the Debye-Hückel term is disregarded in this model.

2.2.The excess Gibbs energy and modeling

The model for the excess Gibbs energy of SLE is expressed as a new formula in this paper.The model is proposed according to the excess Gibbs energy of Pitzer model.Two contributions of the new model are being considered to account for the excess Gibbs energy.The function ofin the excess Gibbs energy function of Pitzer model,andis adopted to account for the electrostatic interaction term between single electrolyte and water.The function ofGexisteraction termbetween saltand salt,which is usually used in multicomponent electrolyte solutions.It is assumed that solubility of every dissolved solid is affected by other solutes in multicomponent electrolyte solutions.For the calculation,water-salt parameters for electrolyte solutions are shared in single salt systems and mixed salt systems.The excess Gibbs energy is described as follows:

Fig.1.The correlation of the activity coefficient for NaCl,KCl,KBr,K2CO3 solutions.Symbols(■,NaCl;,KCl;,KBr;,K2CO3):literature data[13];lines:the correlation result of the new model.

Fig.2.The correlation of the activity coefficient for CaCl2 solution.Symbols(■,CaCl2·2H2O;,CaCl2·4H2O;,CaCl2·6H2O):literature data[23];lines:the correlation result of the new model.

Fig.3.The correlation of the activity coefficient for MgSO4 solution.Symbols(■,MgSO4·7H2O;,MgSO4·6H2O;,MgSO4·H2O):literature data[13,20];lines:the correlation result of the new model.

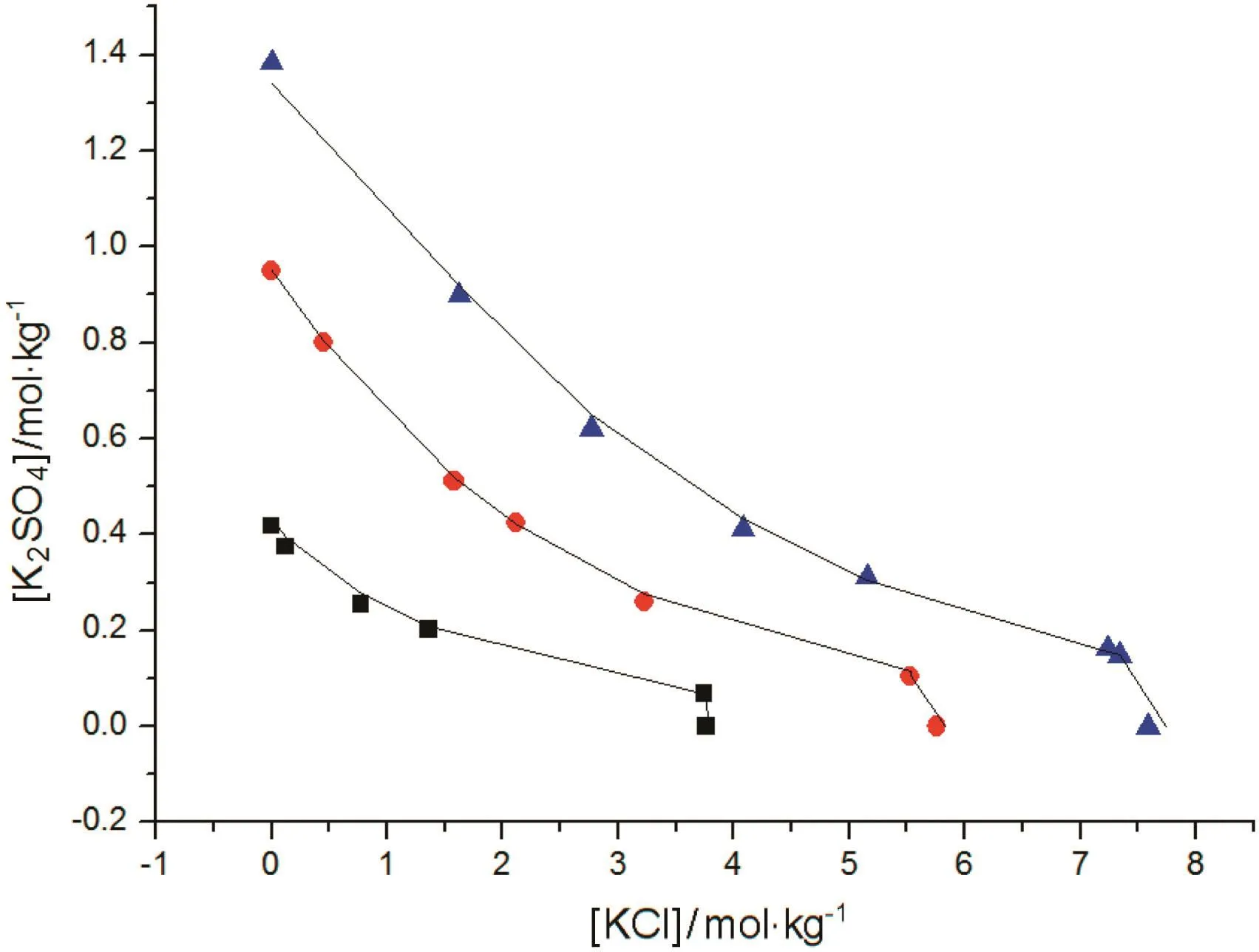
Fig.5.The correlations of SLE data for K2SO4-KCl-H2O system.Symbols(■,T=273.15 K;,T=323.15 K;,T=373.15 K):literature data[13];lines:the correlation result of the new model.

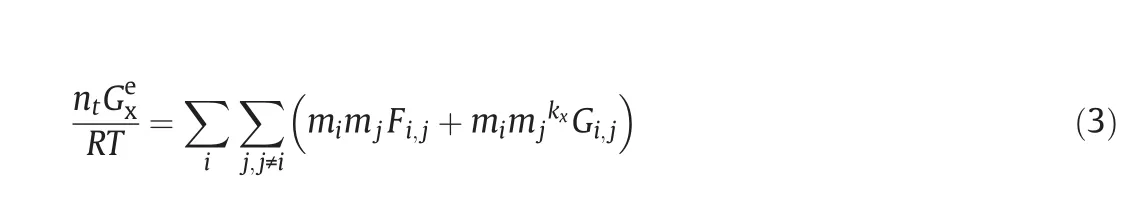
wheremiandmjare the molality of solute;Ei,Fi,jandGi,jare the interaction parameters at a particular temperature;kx=0.5.

In this work,we obtain the activity coefficient of solute from Eqs.(1)-(4),and the final equation can be written as follows:

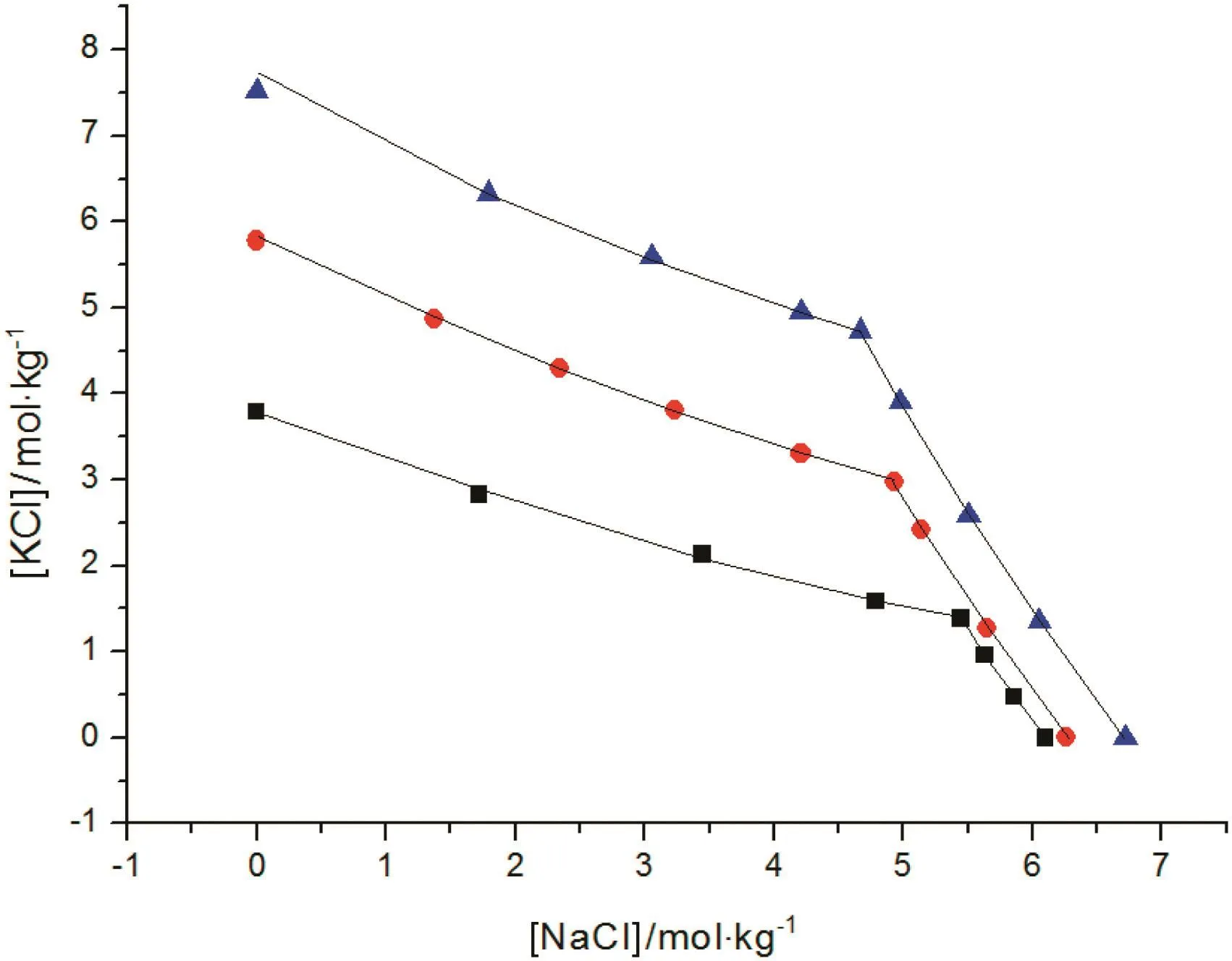
Fig.4.The correlations of SLE data for NaCl-KCl-H2O system.Symbols(■,T=273.15 K;,T=323.15 K;,T=373.15 K):literature data[13,17,23];lines:the correlation result of the new model.

We have tested this approach for SLE data between 273.15 K and 373.15 K.To correlate data at different temperatures,the following temperature dependence of the parameterEi,Fi,jandGi,jwere used:

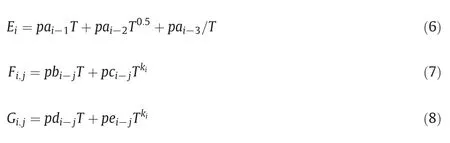
wherepai-1,pai-2andpai-3,are water-solute parameters,pbi-j,pci-j,pdi-jandpei-j,are solute-solute parameters,andkiis the temperature parameter.

Fig.6.The correlations ofSLE data for NaCl-MgCl2-H2Osystem.Symbols(■,T=273.15 K;,T=328.15 K;,T=373.15 K):literature data[13,23];lines:the correlation result of the new model.

Table 2Comparison of the SLE data for single electrolyte solutions

Table 3Literature and calculated values of the solubility of the NaCl-KCl-H2O system

The model is useful only to the calculation of SLE in aqueous salt solutions,it is useful for simple calculations when a comprehensive,multi-property models is not needed and only solubility need to be calculated.Therefore,multiple properties are not considered in this model,such as vapor-liquid equilibria.

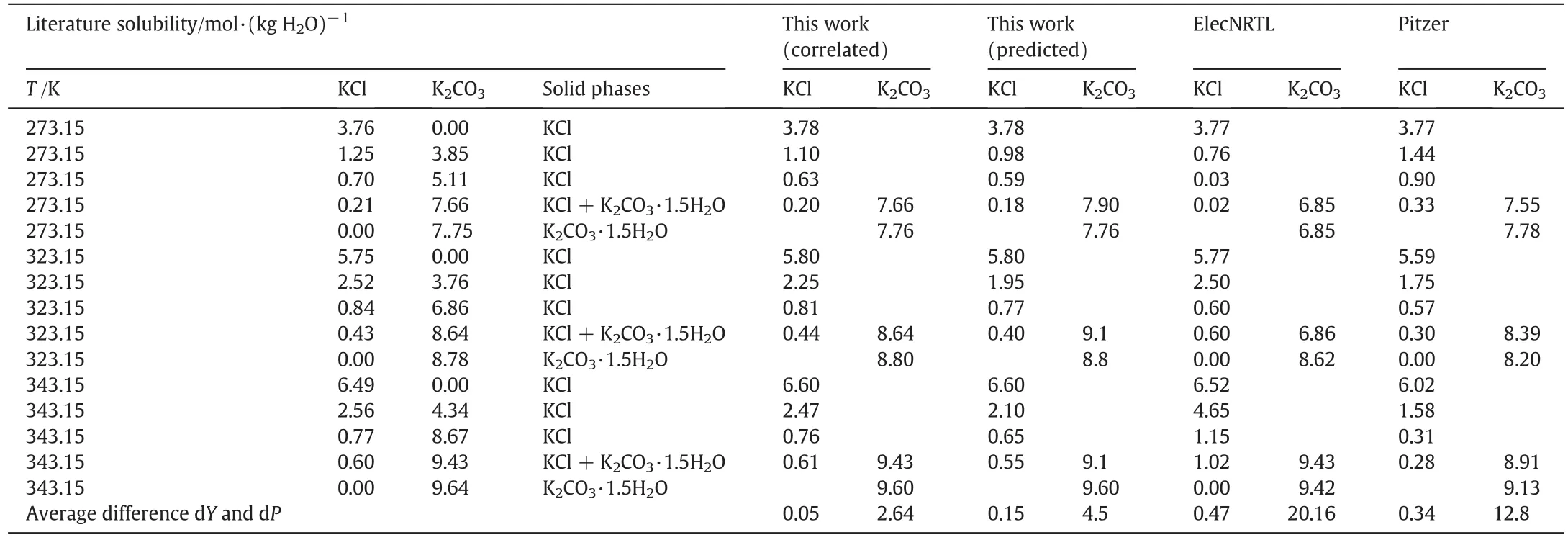
Table 4Literature and calculated values of the solubility of the KCl-K2CO3-H2O system

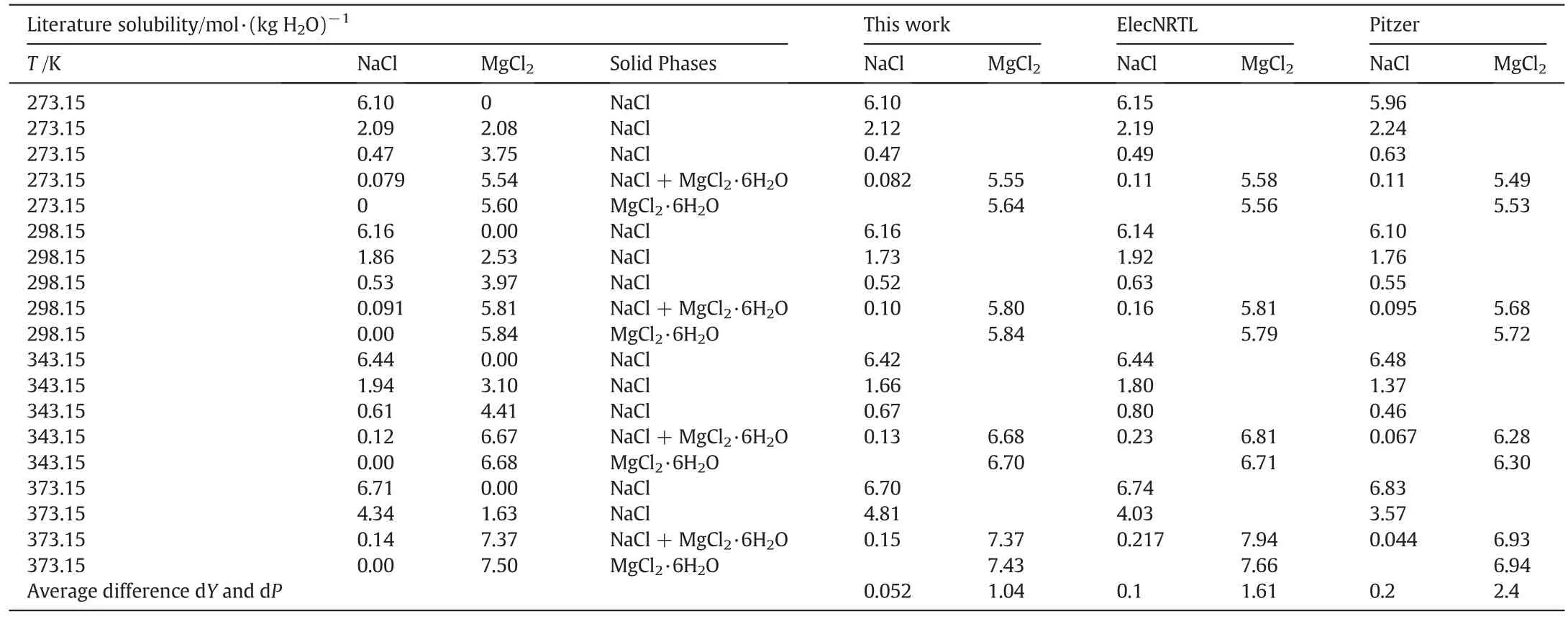
Table 5Literature and calculated values of the solubility of the NaCl-MgCl2-H2O system

Table 6Literature and calculated values of the solubility of the NaCl-Na2SO4-H2O system

2.3.The calculations for SLE

We obtain the activity coefficient expression of solute from Eqs.(1)-(4),the expression for the solute is as follow:

We obtain the activity expression from Eq.(10),and the activity of solute is as follow:

Then,based on the reference state of activity coefficients(ai→1 asmi→the solubility)in this model,the solubility of corresponding solute is obtained.The expression of calculation is as follow:

wheremxis the solubility of solute.

From Eqs.(9)to(12),we can calculate the solubilitymxof corresponding solute.The software of this calculation is 1stopt 6.0,and the computational algorithm is Universal Global Algorithm.

Table 7Literature and calculated values of the solubility of the NaCl-KCl-MgCl2-H2O System

3.Results and Discussion

3.1.Correlation of the SLE in electrolyte solutions

The model described above was used to correlate SLE data fort hirtysix electrolyte solutions at temperature between 273.15 K and 373.15 K.

Results of seventeen mixed electrolyte solutions are presented in Table 1.The results show that for all seventeen systems:dY≤ 0.29 mol·kg-1and the average of dY=0.105 mol·kg-1,dP≤5.8%,and the average of dP=3.4%.

dYand dPwere used:

The correlation of the activity coefficient of NaCl,KCl,KBr,K2CO3is shown in Fig.1,and the results of CaCl2and MgSO4are shown in Figs.2 and 3,respectively.The correlations of SLE data over the solutions of NaCl-KCl-H2O,K2SO4-KCl-H2O and NaCl-MgCl2-H2O at different temperature are shown in Figs.4,5 and 6,respectively.For these electrolyte solution systems,the model provides satisfactory results.In this work,Tables 8 and 9 present the values of the parameters introduced in Eq.(9),the water-solute parameters are listed in Table 8,the solutesolute parameters are listed in Table 9.

3.2.Prediction of the SLE in mixed electrolyte solutions

The predictive capability of the model was examined by calculating SLE in mixed electrolyte solution systems using values of the parameters obtained from the correlation of binary electrolyte solution systems.The prediction of SLE data over the solutions of NaCl+KCl+H2O and KCl-K2CO3-H2O are shown in Tables 4 and 5,respectively.

Table 8Water-salt parameters for electrolyte solutions

Table 9Salt-salt parameters for electrolyte solutions

Table 9(continued)

3.3.Comparison with other methods

Eight single electrolyte solution systems and five mixed electrolyte solution systems were selected for comparison with ElecNRTL,Pitzer and the proposed model in this work,as these system had been previously studied using other methods.However,the ElecNRTL and Pitzer models are comprehensive thermodynamic models that reproduce multiple properties,including vapor-liquid equili bria,activity coefficients,and caloric properties in addition to solubility,the new model is useful for simple calculations when a comprehensive,multi property model is not need and only solubility data need to be correlated.

Results of comparisons for single electrolyte solution systems are shown in Table 2,where dYand dPare listed.Note that the maximum dY(=0.37 mol·kg-1)and the maximum dP(=4.16%)of the model in this work are less than ElecNRTL's(dY=2.41 mol·kg-1,dP=61.37%)and Pitzer's(dY=1.16 mol·kg-1,dP=25.24%).Similarly,the average dY(=0.11 mol·kg-1)and the average dP(=1.85%)of the model are less than ElecNRTL's(dY=0.68 mol·kg-1,dP=12.7%)and Pitzer's(dY=0.37 mol·kg-1,dP=6.12%).

Results of comparisons for mixed electrolyte solution systems are shown in Tables 3-7.These systems are NaCl-KCl-H2O,KCl-K2CO3-H2O,NaCl-MgCl2-H2O,NaCl-Na2SO4-H2O and NaCl-KCl-MgCl2-H2O,respectively. The average dY(=0.026, 0.05, 0.052, 0.036,0.055 mol·kg-1)and the average dP(=0.56,2.64,1.04,2.78,3.7%)of this work are less than ElecNRTL's(dY=0.20,0.47,0.1,0.26,0.28 mol·kg-1,dP=5.8,20.16,1.61,22.5,24.2%)and Pitzer's(dY=0.20,0.34,0.2,0.12,0.082 mol·kg-1,dP=5.59,12.8,2.4,7.8,6.57%).

These comparisons show that the model in this work can be used to correlate SLE data over wide ranges of temperatures and concentrations,and the results are better than ElecNRTL's and Pitzer's.

4.Conclusions

In this work,a new model is developed for the calculation of SLE in electrolyte solutions.A new excess Gibbs energy equation for SLE and a new assumption for the reference state of activity coefficients are proposed in the model.The new model was applied to single electrolyte solution and mixed electrolyte solution systems containing a variety of salts at wide ranges of temperature,and the results yielded compared well with literature data and with published models.The model can successfully correlate SLE data in electrolyte solutions,and the results are better than ElecNRTL's and Pitzer's.

Nomenclature

aactivity

cal calculation

dYaverage absolute error,mol·kg-1

dPaverage relative error,%

exp experiment

Geexcess Gibbs energy,J·mol-1

electrostatic interaction between single electrolyte and water,J·mol-1

electrostatic interaction term between salt and salt,J·mol-1

icomponenti

jcomponentj

kitemperature parameter

kxexponential parameter

mmolality,mol·kg-1

mxsolubility,mol·kg-1

ntintegral molar quantity,mol

pawater-solute parameter

pb,pc,pd,pesolute-solute parameters

Rgas constant,J·mol-1·kg-1

Ttemperature,K

γ activity coefficients

[1]C.C.Chen,H.I.Britt,J.F.Boston,et al.,Local composition model for excess Gibbs energy of electrolyte systems.Part I:Single solvent,single completely dissociated electrolyte systems,AICHE J.28(4)(1982)588-596.

[2]C.C.Chen,L.B.Evans,A local composition model for the excess Gibbs energy of aqueous electrolyte systems,AICHE J.32(3)(1986)444-454.

[3]C.C.Chen,P.M.Mathias,H.Orbey,Use of hydration and dissociation chemistries with the electrolyte-NRTL model,AICHE J.45(7)(1999)1576-1586.

[4]K.S.Pitzer,Thermodynamics of electrolytes.I.Theoretical basis and general equations,J.Phys.Chem.77(2)(1973)268-277.

[5]P.Wang,A.Anderko,R.D.Young,A speciation-based model for mixed-solvent electrolyte systems,Fluid Phase Equilib.203(1)(2002)141-176.

[6]P.Wang,A.Anderko,Springer R.D.,et al.,Modeling phase equilibria and speciation in mixed-solvent electrolyte systems:II.Liquid-liquid equilibria and properties of associating electrolyte solutions,J.Mol.Liq.125(1)(2006)37-44.

[7]X.Lu,G.Maurer,Model for describing activity coefficients in mixed electrolyte aqueous solutions,AICHE J.39(9)(1993)1527-1538.

[8]X.Lu,L.Zhang,Y.Wang,et al.,Prediction of activity coefficients of electrolytes in aqueous solutions at high temperatures,Ind.Eng.Chem.Res.35(5)(1996)1777-1784.

[9]P.Debye,E.Hückel,De la theorie des electrolytes.I.abaissement du point de congelation et phenomenes associes,Phys.Z.24(9)(1923)185-206.

[10]K.Thomsen,P.Rasmussen,R.Gani,Simulation and optimization of fractional crystallization processes,Chem.Eng.Sci.53(8)(1998)1551-1564.

[11]K.Thomsen,P.Rasmussen,Modeling of vapor-liquid-solid equilibrium in gasaqueous electrolyte systems,Chem.Eng.Sci.54(12)(1999)1787-1802.

[12]X.Xu,Y.Hu,L.Wu,et al.,Experimental and modeling of vapor-liquid equilibria for electrolyte solution systems,J.Chem.Eng.Data59(11)(2014)3741-3748.

[13]S.Howard,L.Silcock,Solubilities of inorganic and organic compounds,3(2),Pergamon Press,1979 359-370.

[14]W.J.Lightfoot,C.F.Prutton,Equilibria in saturated salt solutions.II.The ternary systems CaCl2-MgCl2-H2O,CaCl2-KCl-H2O and MgCl2-KCl-H2O at 75°C,J.Am.Chem.Soc.69(9)(1947)2098-2100.

[15]V.I.Vereshchagina,Zolotareva L.V.,L.F.Shulyak,Zh.Neorg.Khim.14(1969)3390.

[16]W.J.Lightfoot,Prutton C.F,Equilibria in saturated solutions.I.The ternary systems CaCl2-MgCl2-H2O,CaCl2-KCl-H2O,and MgCl2-KCl-H2O at 35°C,J.Am.Chem.Soc.68(6)(1946)1001-1002.

[17]A.Apelblat,E.Korin,Temperature dependence of vapor pressures over saturated aqueous solutions at invariant points of the NaCl+ KCl+ H2O,NaCl+NaNO3+H2O,KCl+KBr+H2O,KCl+KI+H2O,KCl+KNO3+H2O,and KCl+K2SO4+H2O systems†,J.Chem.Eng.Data54(5)(2009)1619-1624.

[18]J.W.Leather,J.N.Mukerji,J.N.Mukerji,The system potassium nitrate,sodium chloride,water,Thacker Spink,1914.

[19]Assarsson G.O.,Equilibria in aqueous systems containing K+,Na+,Ca+2,Mg+2and Cl-.I.The ternary system CaCl2-KCl-H2O1,J.Am.Chem.Soc.72(4)(1950)1433-1436.

[20]N.V.Bodaleva,I.N.Lepeshkov,Solubility study in the system K2SO4-MgSO4-CaSO4-H2O at 55°C,Zh.Neorg.Khim.1(1956)995-1007.

[21]L.V.Novikova,A study of solubility for the system CaSO4·MgSO4·H2O at 35°by the method of tracer atoms,Zh.Neorg.Khim.2(1957)662-668.

[22]H.Li,D.Zeng,Y.Yao,et al.,Solubility phase diagram of the quaternary system Li+,Mg2+//Cl-,—H2O at 298.15 K:Literature redetermination and model simulation,Ind.Eng.Chem.Res.53(18)(2014)7579-7590.

[23]M.A.Clynne,R.W.I.Potter,J.L.J.Haas,Solubility of NaCl in Aqueous Electrolyte Solutions from 10 to 100 degrees C,J.Chem.Eng.Data26(1981)396-398.

[24]J.E.Teeple,The industrial development of searles lake brines with equilibrium data,1929.

[25]E.C.Tavares,S.I.S.Marcelino,O.Chiavone-Filho,C.P.Souza,Determination of salt solubility data for ternary aqueous systems with a quasiisothermic thermometric technique,Thermochim.Acta328(1999)253-258.

[26]J.Nývlt,J.Eysseltová,Physical interpretation of solubility interaction constants from the series expansion of the relative activity coefficients,Collect.Czechoslov.Chem.Commun.59(9)(1994)1911-1921.