基于改进的逐点交叉验证的RBF形态参数优化方法及其空间插值实验

李 佳,段 平*,吕 海 洋,张 思 阳,盛 业 华

(1.云南师范大学旅游与地理科学学院，云南 昆明 650050;2.虚拟地理环境教育部重点实验室(南京师范大学)，江苏 南京 210023;3.江苏省地理环境演化国家重点实验室培育建设点，江苏 南京 210023)

基于改进的逐点交叉验证的RBF形态参数优化方法及其空间插值实验

李 佳1,2,3,段 平1,2,3*,吕 海 洋2,3,张 思 阳2,3,盛 业 华2,3

(1.云南师范大学旅游与地理科学学院，云南 昆明 650050;2.虚拟地理环境教育部重点实验室(南京师范大学)，江苏 南京 210023;3.江苏省地理环境演化国家重点实验室培育建设点，江苏 南京 210023)

径向基函数(Radial Basis Function，RBF)是一种确定性的多维空间插值模型，可以有效逼近任意维度的空间数据。RBF插值模型中，基函数形态参数直接影响插值精度。为了快速求解最佳形态参数，获取准确的插值结果，该文采用改进的逐点交叉验证(Improved Leave One Out Cross Validation，ILOOCV)方法求取最优形态参数，首先从形态参数取值区间内选定初始形态参数α，然后从n个已知点中顺序选出一个点，使用剩下的n-1个已知点构建RBF插值模型，计算被取出点处真实值与插值结果的误差，循环n次，累计交叉验证误差，再依次从形态参数取值区间选取下一个值，重复操作，建立形态参数α与累计交叉验证误差之间的函数映射关系，最后通过最小化交叉验证误差来获取最佳形态参数。以我国东北地区气象观测数据进行实验，对ILOOCV方法进行验证，结果表明ILOOCV方法选取最佳形态参数使其插值结果比较精确，是一种可行的RBF形态参数优化方法。

空间插值；径向基函数；形态参数；逐点交叉验证

0 引言

空间插值是GIS进行地理分析的重要方法[1]。Franke从插值效果、参数灵敏度、执行时间、存储要求及编程实现的难易程度等方面对多种插值方法进行比较，得出RBF插值是一种较优的空间插值方法[2]。使用RBF插值方法进行空间插值需要解决两个问题：基函数的选取和形态参数的优化。每种基函数的特性各有不同，但只要采样点足够密，都可以准确地逼近几乎所有函数[3]，故其插值结果差异不大。在基函数确定后，形态参数的选取直接影响到插值结果的精度[4]，只有合理选取形态参数才能准确地重建地理空间场。

以中国东北地区气温观测数据为实验对象，结合气温数据自身的特性，在使用RBF插值模型时采用ILOOCV方法求解最佳形态参数，并将插值结果与通过经验最佳形态参数的插值结果进行对比分析，最终验证ILOOCV形态参数优化方法及其空间插值的可靠性和有效性。

1 RBF最优形态参数的求解

1.1RBF插值模型

RBF插值方法是一种不需对数据做任何假设，直接利用已知数据本身来准确逼近任意维度空间曲面，并对任意位置估计其函数值的理论和方法。设多维空间n个已知点，使用向量xi表示第i个已知点，则RBF插值模型可以表示为：

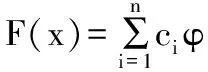
(1)

1.2 基于LOOCV的RBF最优形态参数求解方法

采用任何一种基函数进行空间插值，都会随着α增大(到达某个临界值之前)，插值模型越来越光滑，若超过这个临界值，继续增加α，则插值模型连续性变差，误差随之变大，将该α的临界值称为最佳形态参数。为了获取精确的插值模型，需要采用一个合理的计算方法得到最佳形态参数，常见的计算方法是LOOCV。首先将已知点集划分为插值点集和验证点集，使用插值点集对该研究区域进行RBF插值，并计算验证点集处的插值结果，与验证点集处的真实值进行对比，通过使插值结果与真实值间的误差最小化来获取最佳的形态参数。具体步骤是：

步骤1：设定形态参数选取区间[p，q](其中0≤p≤q)，以s(s<1且随区间大小不断调整)为步长，从小到大依次取值αi，带入RBF插值模型；

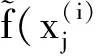
(2)

步骤4：重复步骤2、3，循环n次，直至所有观测点参与到交叉验证过程，记录其累计误差：

(3)

步骤5：根据形态参数取值步长s，依次取值重复步骤1、2、3，直至区间上限，构建形态参数与累计误差映射关系LOOCV(αi)；

步骤6：求解LOOCV(αi)累计误差的最小值，其对应的形态参数αi作为最佳形态参数。

在LOOCV求解过程中径向基函数模型求解时间复杂度为O(n3)，进行n次交叉验证时间复杂度为O(n4)。使用该方法计算最佳形态参数，面临运算量大、效率低问题，需对其进行改进。

1.3 基于ILOOCV的RBF最优形态参数求解方法

数学上可证明，在LOOCV求解和RBF插值模型求解过程中，存在如下数学关系[8]：

(4)

(5)

则1.2节中步骤2、3、4可以简化为：步骤 2：使用全部已知点和形态参数αi，计算插值矩阵Φ和线性组合系数c，根据式(5)计算交叉验证误差。本文基于式(5)求解最佳形态参数和RBF插值模型。

2 实验分析

2.1 空间插值实验数据源与预处理

为了验证ILOOCV方法在地理空间现象插值中的可靠性，实验数据来源于中国气象科学数据共享服务网(http://cdc.cma.gov.cn/home.do)，选取中国东北地区123个观测站点的地面气候标准值年值数据集(1981-2010年)累年年平均气温作为插值对象。如图1所示，观测站点呈非均匀散乱分布；在辽宁省、吉林省部分区域，观测站点分布较为密集，而黑龙江省和内蒙古部分区域分布较为稀疏；气温值从南向北、由东向西逐渐降低，整体变化比较平稳。

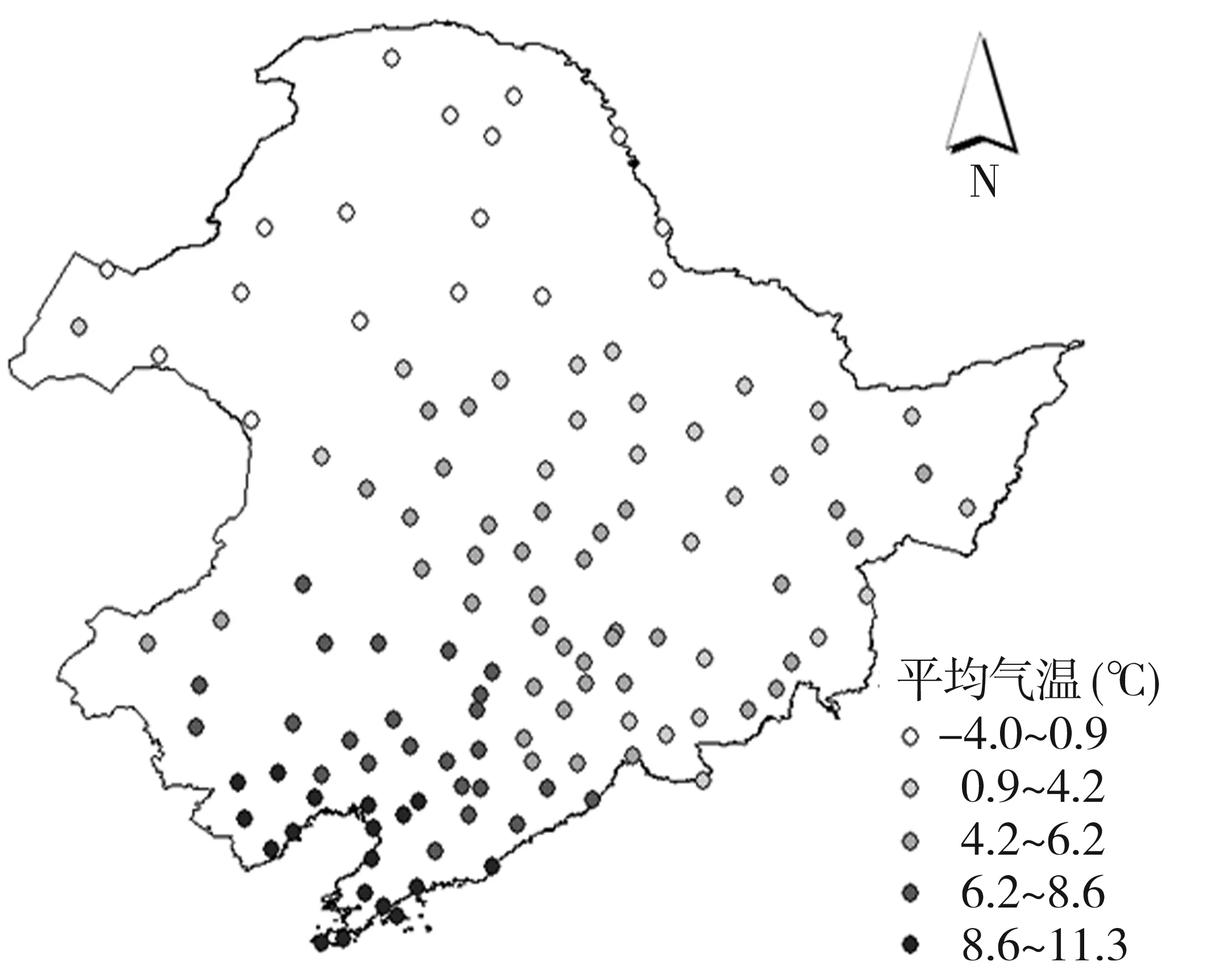
图1 原始数据Fig.1 Original data

插值前对数据点进行预处理，采用ASTER网站(http://asterweb.jbl.nasa.gov/gdem.asp)提供的DEM(30 m*30 m)对不同高度的插值结果进行气温修正处理，其中气温直减率为0.6°C/100 m[11,12]，插值及修正过程如下：

步骤1：根据DEM高程信息，将原始数据中的气温值根据式(6)修正到海平面高度的真实值；

t1=t0+r×h

(6)

步骤2：对修正后的气温数据采用ILOOCV方法求解最佳形态参数，再进行RBF插值重建气温场；

步骤3：使用DEM高程信息根据式(7)将插值得到的气温场进行再次修正，使得插值结果能够准确地表达地表的真实气温。

t2=t1-r×h

(7)

其中，t0为真实气温数据，t1为修正到海平面的气温数据，t2为再次修正后的真实气温数据，r为气温直减率(0.6°C/100m)，h为海拔。

2.2 几种常见的插值方法精度分析

对123个观测站点数据进行高程修正后分别采用反距离权重(InverseDistanceWeight，IDW)、普通克里金(OrdinaryKriging，OK)、Frank建议的经验形态参数RBF插值(Frank-RBF)、基于ILOOCV的RBF(ILOOCV-RBF)4种空间插值方法对东北地区气温数据进行逐点交叉验证，其中每种插值方法参考点设置为最小点数为10个，最大点数为15个，普通克里金的变异函数拟合模型为球状模型，RBF基函数采用Multiquadric。插值精度分析采用最大误差(MaxError)、最小误差(MinError)、平均误差(MeanError，ME)、均方根误差(RootMeanSquareError，RMSE)，各插值方法的精度如表1所示。

表1 插值误差Table 1 Interpolation error

表1中IDW插值方法除Min Error优于其他3种空间插值方法外，另外3个误差指标Max Error、ME和RMSE都最大，原因可能是IDW插值估算的属性值只能在参考点属性值域中，IDW插值方法性质决定了估算值不能大于参考点属性值的最大值和小于参考点属性值的最小值。OK插值中Max Error、Min Error误差与ILOOCV-RBF相差不大，但是ME、RMSE相差较大，而ME、RMSE最能反映出插值方法的精度。因为Frank-RBF和ILOOCV-RBF插值原理一样，所以二者插值误差较为近似，但是Frank-RBF的误差略大，原因是其采用的是经验形态参数。总体上ILOOCV-RBF插值误差均小于其他3种插值误差。

2.3 基于ILOOCV的RBF气温场重建与分析

使用ILOOCV-RBF方法求解该区域内RBF插值模型的最佳形态参数为α=0.2248，根据获取的最佳形态参数，构建该区域RBF插值模型，对该区域气温场进行重建(图2)，重建结果光滑连续，局部细节特征表达完好。

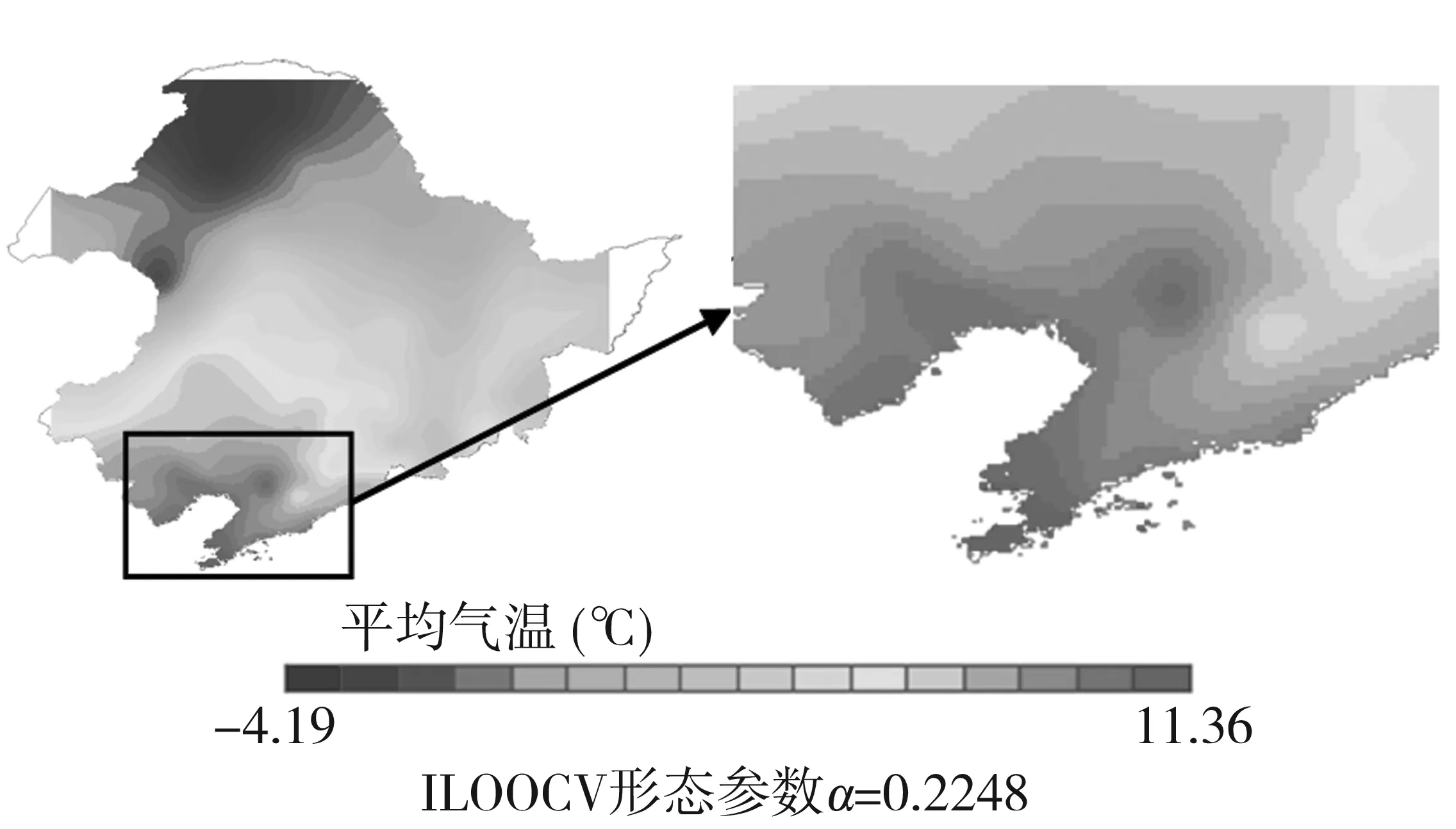
图2 插值结果Fig.2 Interpolation results

为了分析整个区域内气温场插值重建结果的误差分布情况，以区域内各个观测站点的交叉验证误差为研究对象，对区域误差分布情况进行RBF插值，采用ILOOCV方法获取RBF插值模型的最佳形态参数，求解该区域内的RBF误差插值模型，对误差进行分级，结果如图3所示。

图3 误差分布Fig.3 Error distribution

该区域内的误差分布具有以下特征：1)区域内气温场插值重建结果整体误差较小，局部存在较大误差；2)误差主要集中在西北部区域，而中部区域误差较小，误差分布与区域地形变化有一定的相关性。

结合区域内的DEM数据(图4)和观测站点分布情况(图1)以及观测站点气温观测值变化情况，进一步分析气温场插值重建误差产生的原因：1)区域西北部海拔较高，对冷空气形成一定阻挡，平均气温较低，为多年冻土地带，因此，该区域内的气温值要低于其他区域，即气温值属性在本区域与相邻区域出现了较大的差异；2)区域西北部气温值与邻近区域变化较大并且观测站数量相对较少，不能够很好地反映区域内的气温值变化情况，而区域中部气温值变化较为平缓且观测站点较多。

图4 区域DEMFig.4 DEM of the study area

3 结语

使用RBF模型进行地理空间插值时，形态参数的选取直接影响到插值结果的精度。本文基于ILOOCV方法，使用中国东北地区地面累年年平均气温数据进行实验，获取最佳形态参数进行RBF气温场插值重建，虽然存在部分插值误差，但整体结果较为准确，可以有效地反映区域内的气温变化情况。

[1] 李新,程国栋,卢玲.空间内插方法比较[J].地球科学进展,2000,15(3):260-265.

[2] FRANKE R.Scattered data interpolation:Tests of some methods[J].Mathematics of Computation,1982,38(157):181-200.

[3]WENDLAND H.Scattered Data Approximation[M].Cambridge:Cambridge University Press,2005.

[4] ROUSSOS G,BAXTER B J C.Rapid evaluation of radial basis functions[J].Journal of Computational and Applied Mathematics,2005,180(1):51-70.

[5] HARDY R L.Multiquadric equations of topography and other irregular surfaces[J].Journal of Geophysical Research,1971,76(8):1905-1915.

[6] 欧阳洁,聂玉峰,车刚明,等.数值分析[M].北京：高等教育出版社,2009.

[7] DAVIS B M.Uses and abuses of cross-validation in geostatistics[J].Mathematical Geology,1987,19(3):241-248.

[8] RIPPA S.An algorithm for selecting a good value for the parameter c in radial basis function interpolation[J].Advances in Computational Mathematics,1999,11(2-3):193-210.

[9] FASSHAUER G E.Meshfree Approximation Methods with MATLAB[M].Singapore:World Scientific,2007.

[10] MONGILLO M.Choosing Basis Functions and Shape Parameters for Radial Basis Function Methods.http://www.siam.org/students/siuro/vol4/S01084.pdf，2011.

[11] 陈冬花,邹陈,王苏颖,等.基于 DEM 的伊犁河谷气温空间插值研究[J].光谱学与光谱分析,2011,31(7):1925-1929.

[12] 蔡迪花,郭铌,李崇伟.基于 DEM 的气温插值方法研究[J].干旱气象,2009,27(1):10-17.

RBF Shape Parameter Optimization Approach Based on ILOOCV and Its Spatial Interpolation Experiments

LI Jia1,2,3,DUAN Ping1,2,3,LYU Hai-yang2,3,ZHANG Si-yang2,3,SHENG Ye-hua2,3

(1.SchoolofTourismandGeographicalSciencesofYunnanNormalUniversity,Kunming650050;2.KeyLaboratoryofVirtualGeographicEnvironment(NanjingNormalUniversity),MinistryofEducation,Nanjing210023;3.StateKeyLaboratoryCultivationBaseofGeographicalEnvironmentEvolution(JiangsuProvince),Nanjing210023,China)

Radial Basis Function (RBF) can effectively approximate arbitrary dimension spatial data,which is a deterministic multivariate spatial interpolation method.In RBF interpolation model,the shape parameter in the basis function has a directimpact on the accuracy of the interpolation.In order to get optimal shape parameter which leads to smallest interpolation error and obtains the most accurate interpolated results,the Improved Leave One Out Cross Validation (ILOOCV) approach is applied in this paper.First,the initial shape parameter α is selected from the shape parameter interval which are divided by the step const value,then sequentially choose one point from thenknown points as the verify point and use then-1 remaining known points to calculate the RBF interpolation model.After that,the interpolated value of the point which are taken away from thenknown points by the RBF interpolation model is calculated and compared with the true value of the known point to get the interpolation error,then these operations are repeated forntimes until all the points are left out to be chosen as the verify point and the cross validation interpolation error is accumulated.After all these steps have been done,another shape parameter from the shape parameter interval is taken according to the step const value and the leave one out cross validation is repeated until all the shape parameters have been used to calculate the accumulated cross validation interpolation error,then the mapping relationship between the selected shape parameter and the accumulated cross validation interpolation error is established.Finally,to minimize the accumulated cross validation interpolation error in each leave one out cross validation process to get the smallest error and take the corresponding α as the optimal shape parameter.The meteorological observation data in Northeast China are taken as examples to verify the feasibility and effectiveness of this approach.Results show that,the optimal shape parameter selected by ILOOCV turns out to be effective and the spatial interpolated results are quite accurate.

spatial interpolation;radial basis function;shape parameter;leave one out cross validation

2015-10-03；

2016-01-16

国家自然科学基金项目(41271383)；云南师范大学博士基金项目(01300205020503113)

李佳(1984-)，女，博士，讲师,主要从事空间分析、近景摄影测量等研究。*通讯作者E-mail:duanpingshai@163.com

10.3969/j.issn.1672-0504.2016.03.008

P208

A

1672-0504(2016)03-0039-04