光谱角余弦与相关系数测度组合的光谱匹配分类方法与实验

魏 祥 坡，余 旭 初，付 琼 莹，刘 冰，薛 志 祥

(信息工程大学，河南 郑州 450001)

光谱角余弦与相关系数测度组合的光谱匹配分类方法与实验

魏 祥 坡，余 旭 初，付 琼 莹，刘 冰，薛 志 祥

(信息工程大学，河南 郑州 450001)

光谱相似性测度是高光谱影像光谱匹配分类的准则，但单一的光谱相似性测度不能综合考虑光谱曲线的形状、辐射等多种特征，因此将其用于高光谱影像光谱匹配分类时精度较低，研究发现两种或多种相似性测度的组合能够有效提高光谱匹配分类的精度。在光谱角余弦测度和相关系数测度的基础上，采用算术平均的组合方式，得到光谱角余弦-相关系数测度，将其用于光谱匹配分类，实现光谱角余弦与相关系数测度组合的光谱匹配分类方法。提出了基于光谱角余弦-相关系数测度的光谱匹配分类流程，通过ROSIS和OMIS两组高光谱影像分类实验表明，相比于光谱角余弦测度和相关系数测度，将光谱角余弦-相关系数测度用于光谱匹配分类能够得到较高的总体分类精度，对单一地物的分类精度也有一定程度的改善。

高光谱影像；光谱角余弦-相关系数测度；分类；精度

0 引言

高光谱遥感可在可见光至近红外的电磁波谱范围内获得大量光谱间隔窄、近似连续的图像数据，能够探测出精细的地物属性信息[1,2]。凭借其高光谱分辨率的优势，高光谱遥感在植被调查、环境监测、精准农业、城市调查、矿物勘探、地质勘查、灾害评估和专题图制作等民用领域，以及战场环境监测、伪装与反伪装、目标侦查、打击效果评估等军事领域得到了广泛应用[3,4]。

相比于全色和多光谱影像，高光谱影像具有丰富的光谱信息。高光谱影像分类方法[5]包括基于光谱特征的分类方法[6]和基于统计特征的分类方法[7]，其中光谱匹配分类是根据光谱曲线之间的差别对像元进行分类，能够充分利用影像中丰富的光谱信息。光谱相似性测度是光谱匹配分类准则，常用的光谱相似性测度包括欧氏距离(Euclidean Distance，ED)[8]、光谱角余弦(Spectral Angle Cosine，SAC)[9,10]、光谱相关系数(Spectral Correlation Coefficient，SCC)[11-13]、光谱信息散度(Spectral Information Divergence，SID)[14]等。

然而，单一的光谱相似性测度只考虑了光谱曲线某一方面的特征，不能完整地描述光谱曲线的形态，分类效果并不好，国内外专家针对该问题提出了很多改进方法，安斌等[15]结合光谱角余弦和欧氏距离提出了光谱角余弦-欧氏距离测度，分类精度优于采用单一光谱相似性测度的分类方法；孔祥兵等[16]在几何距离、相关系数和相对熵的基础上提出了一种光谱泛相似性测度，在进行光谱相似性分析时，综合考虑光谱矢量大小、光谱曲线形状和光谱信息量等光谱特征信息，能够得到更好的光谱识别结果。

本文将光谱角余弦-相关系数测度引入到高光谱遥感影像的光谱匹配分类中，在光谱角余弦测度和光谱相关系数测度的基础上，构造光谱角余弦-相关系数测度，实现基于光谱匹配的高光谱影像分类。利用ROSIS和OMIS高光谱影像，分别采用光谱角余弦测度、光谱相关系数测度和光谱角余弦-相关系数测度进行分类对比，实验结果表明本文提出的光谱角余弦-相关系数测度不仅能提高影像的总体分类精度，而且对单类地物的分类精度也有一定程度的改善。

1 光谱相似性测度

1.1 传统光谱相似性测度

传统的光谱相似性测度分为几何空间测度和概率空间测度，几何空间测度是在高维空间中，将光谱向量视为空间中的一个点，两点间的广义空间距离表示光谱向量的相似性，主要包括欧氏距离、兰氏距离等距离测度和光谱角余弦等角度测度。概率空间测度基于统计学理论，将光谱向量视为一个随机变量，利用概率论和数理统计方法对两个光谱向量之间的相似性测度进行分析，主要包括光谱相关系数和光谱信息散度等。

(1)光谱角度测度。光谱角度测度通过计算光谱向量间的夹角来描述光谱曲线形状间的相似性，两个光谱特征间的广义夹角可表示为：

(1)

其中，Ti和Ri分别代表测试光谱和参考光谱中第i波段的反射值，n为光谱曲线波段数，θ为光谱向量之间的广义夹角即光谱角(SpectralAngle,SA)。

(2)

(3)

其中n为波段数。

则光谱曲线之间的相关系数可以表示为：

(4)

1.2 光谱角余弦-相关系数测度

传统的基于相似性测度的光谱匹配方法通常使用单一光谱相似性测度进行光谱匹配分类，但单一的光谱相似性测度往往存在缺陷，只利用了光谱曲线某一方面的特征，如最小距离测度利用了光谱曲线之间的距离度量，光谱角余弦测度利用了光谱曲线之间的形状度量。研究证明，两种或多种相似性测度的结合可以有效提高光谱匹配分类的精度，本文将考虑光谱向量间广义夹角的光谱角余弦测度和考虑光谱曲线整体形状的光谱相关系数测度结合形成光谱角余弦-相关系数测度。由于相关系数测度的计算公式涉及两条光谱曲线不同波段反射值之间的运算，为了使公式简练，设x和y为不同像元的n维光谱向量，xi和yi为光谱向量第i波段的值，则光谱角余弦测度的计算公式为：

(5)

相关系数测度的计算公式为：

(6)

光谱角余弦cosθ的取值范围为[0,1]，聚类原则为“值越大，光谱曲线越相似”；相关系数r的取值范围为[0,1]，聚类原则为“值越大，光谱曲线越相似”；两种测度有着相同的取值范围和聚类原则，为了减少计算量，分别赋以相同的权重，采用算术平均组合两种相似性测度，形成光谱角余弦-相关系数测度：

SAC-SCC=(cosθ+r)/2=

(7)

SAC-SCC测度的取值范围为[0,1]，聚类准则为“值越大，光谱曲线越相似”。

1.3 基于光谱角余弦-相关系数测度的光谱匹配分类流程

光谱角余弦-相关系数测度联合了几何空间测度和概率空间测度，有效提高了光谱匹配分类的精度。基于光谱角余弦-相关系数测度的光谱匹配分类流程如图1所示：1)根据光谱数据库信息或已知的先验知识，得出各类别的参考光谱曲线；2)采用包络线消除法[17]对高光谱影像进行光谱增强处理，得到消除了包络线的高光谱影像；3)根据公式(7)，对第二步得到的影像测度其中各个光谱曲线与各个参考光谱曲线之间的相似性；4)依据相似性测度的聚类原则，将待分类的光谱曲线归类到相应的类别中，完成光谱匹配分类，利用测试样本进行分类结果的精度评价。

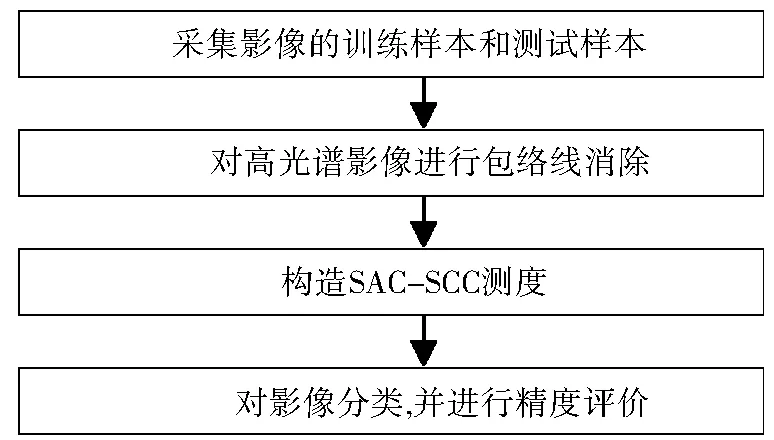
图1 基于光谱角余弦—相关系数测度的光谱匹配分类流程Fig.1 Spectral matching classification process based on SAC-SCC measure

2 实验与分析

光谱角余弦-相关系数测度是在光谱角余弦测度和相关系数测度的基础上组合而成的，因此，本文分别采用光谱角余弦测度、相关系数测度和光谱角余弦-相关系数测度,对ROSIS和OMIS影像进行光谱匹配分类，并比较同一幅影像的不同分类结果在总体分类精度和单一地物分类精度之间的差异。

2.1 ROSIS影像分类实验

实验数据采用德国宇航中心研制的反射式光学系统成像光谱仪(ROSIS)获取的意大利帕维亚大学校园的高光谱影像，影像宽340像元，高610像元，光谱范围为0.43～0.86 um，共115个波段，空间分辨率为1.3 m。去掉受噪声影响较大的波段后余下103个波段进行实验，经过人工判读，该影像中共包含柏油路面、草地、沙砾、树木、金属屋顶、裸土、沥青屋顶、砖块和阴影9种地物类型。由40、90和60波段组成的假彩色图像及采集的样本分布如图2所示(见封2)，样本数量信息如表1所示。

表1 帕维亚大学影像样本数量信息Table 1 Information of sample number in Pavia University imagery

实验过程中，将采集的样本数据中每种地物样本随机选择30%作为训练样本，70%作为测试样本，训练样本作为参考样本计算与影像中各像元之间的相似性测度，测试样本用于计算分类精度。为了提高影像的可分性，对影像数据进行包络线消除处理，然后对处理后的高光谱影像，分别按照光谱角余弦测度、相关系数测度、光谱角余弦-相关系数测度的计算公式，依次计算影像中各像元的光谱曲线与各类别训练样本光谱曲线之间的相似性测度值，并根据“值越小，光谱曲线越相似”的聚类原则，对影像像元进行分类。

采用生产者精度和使用者精度来评定分类结果的精度，ROSIS影像的光谱角余弦测度、相关系数测度、光谱角余弦-相关系数测度的分类结果精度评定见表2、表3，表中加粗数字为同种地物在三种测度中最高的分类精度。

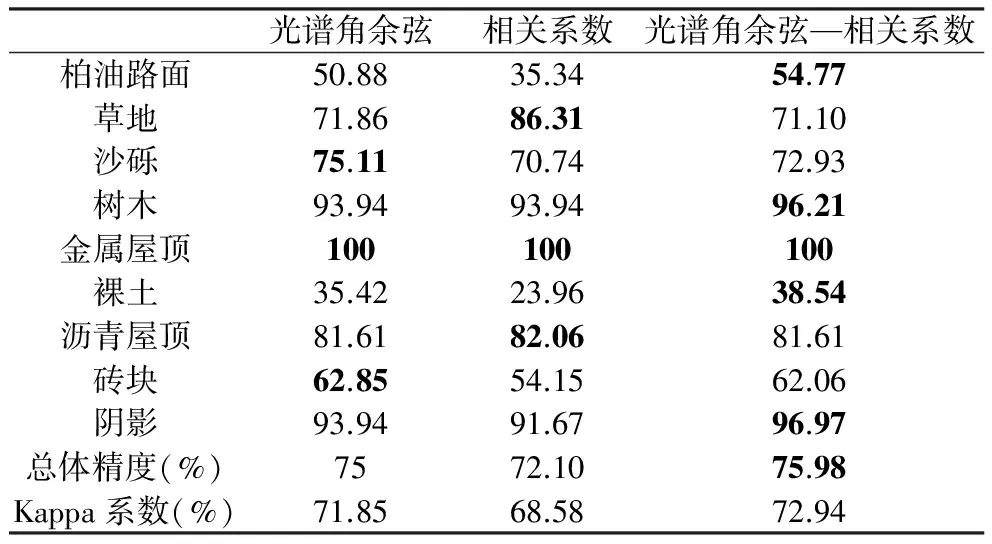
表2 帕维亚大学分类结果精度评定(生产者精度：%)Table 2 Producer accuracy of classification results of Pavia University imagery

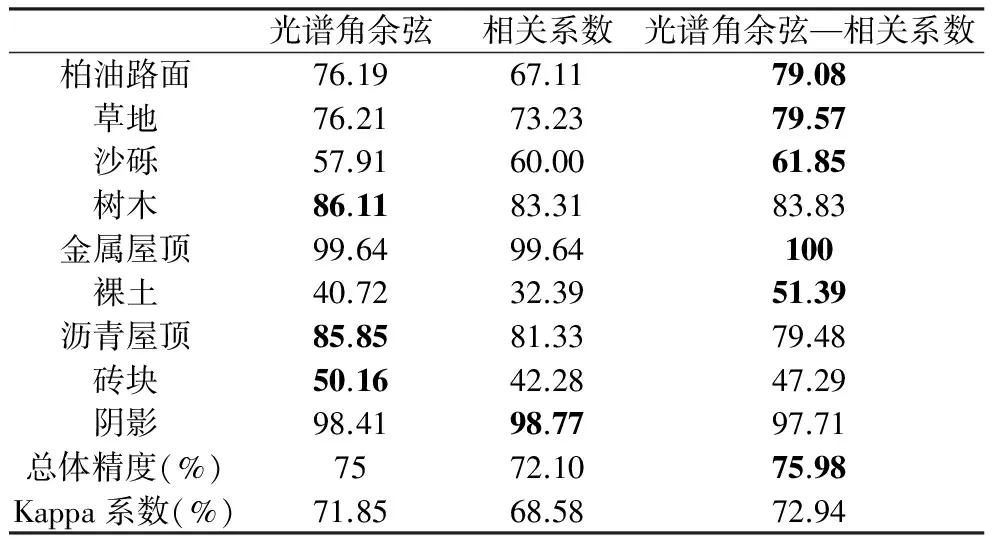
表3 帕维亚大学分类结果精度评定(使用者精度:%)Table 3 User accuracy of classification results of Pavia University imagery

ROSIS影像基于光谱角余弦测度、相关系数测度和光谱角余弦—相关系数测度的光谱匹配分类结果如图3所示。

图3 帕维亚大学影像分类结果Fig.3 Classification results of Pavia University imagery

2.2 OMIS影像分类实验

该实验数据采用由上海技物所研制的实用型模块化成像光谱仪(OMIS)获取的太湖沿岸影像，影像宽347像元，高513像元，光谱范围为0.46～2.85 um，共有128个波段，实验中选择噪声影响较小的6-64、113-128共75个波段，为了处理方便，预先将像元反射率值归一化到[0,1]范围。通过人工判读，影像中共包含7种地物类型，分别为房屋、道路、植被一、植被二、水域、农田和土壤，利用15、115和48波段形成的假彩色影像及影像中样本的采集情况如图4所示(见封2)，其对应的地物类别和样本数量信息如表4所示。

表4 太湖沿岸影像样本数量信息Table 4 Information of sample number in Tai Lake imagery

与ROSIS影像分类实验处理方法相同，分别按照光谱角余弦测度、相关系数测度、光谱角余弦-相关系数测度的计算公式，依次计算影像中各像元的光谱曲线与各类别训练样本光谱曲线之间的相似性测度值，并根据相应的聚类原则对影像像元进行分类。三种测度对应的分类结果精度评定见表5、表6，对应的光谱匹配分类结果如图5所示。

表5 太湖地区影像分类结果精度评定(生产者精度:%)Table 5 Producer accuracy of classification results of Tai Lake imagery

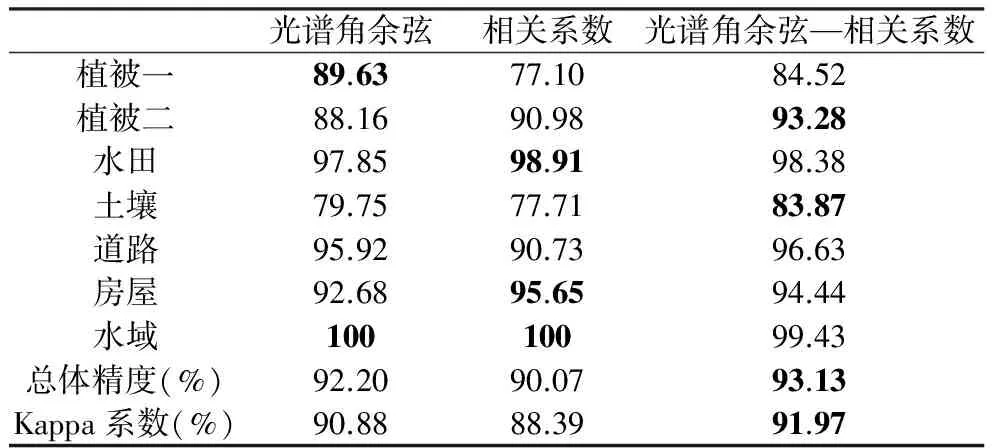
表6 太湖地区影像分类结果精度评定(使用者精度:%)Table 6 User accuracy of classification results of Tai Lake imagery

图5 太湖沿岸影像分类结果Fig.5 Classification results of Tai Lake imagery

2.3 实验分析

通过对比ROSIS影像分类实验和OMIS影像分类实验的结果，可以得出如下结论：1)相比于光谱角余弦测度和相关系数测度，光谱角余弦-相关系数测度对影像光谱匹配分类总体精度有明显的改善；2)相比于光谱角余弦测度和相关系数测度，光谱角余弦-相关系数测度对影像光谱匹配分类单一地物的分类精度有一定程度的提高。

3 结论

本文提出了一种基于光谱角余弦-相关系数测度的高光谱影像光谱匹配分类方法。在传统的光谱角余弦测度和光谱相关系数测度的基础上，将两者加权平均，得出光谱角余弦-相关系数测度，其取值范围和聚类原则不变，用于高光谱影像光谱匹配分类，通过ROSIS和OMIS两组高光谱影像分类实验表明，相比于光谱角余弦测度和相关系数测度，光谱角余弦-相关系数测度对总体分类精度和单一地物分类精度都有一定程度的改善。

光谱角余弦测度和相关系数测度本质上仍是基于光谱曲线的形状特征，因此两者结合而成的光谱角余弦-相关系数测度对个别地物的分类精度仍处于较低的水平，而且光谱角余弦-相关系数测度只是利用了两种相似性测度的算术平均，对不同相似性测度的权重没有系统性的计算，也没有加入空间邻域信息，导致分类结果中仍存在较多的类别噪声，分类精度仍有较大的提高空间。

[1] 童庆禧，张兵，郑兰芬.高光谱遥感[M].北京：高等教育出版社，2006.1-2.

[2] 浦瑞良，宫鹏.高光谱遥感及其应用[M].北京：高等教育出版社，2000.1-4.

[3] 谭熊，余旭初，张鹏强.一种基于模糊混合像元分解的高光谱影像分类算法[J].测绘科学技术学报，2013,30(3)：279-283.

[4] 杨国鹏，余旭初，冯伍法，等.高光谱遥感技术的发展与应用现状[J].测绘通报,2008(10):1-4.

[5] 许卫东.高光谱遥感分类与提取技术[J].红外，2004,24(5)：28-34.

[6] 苏红军，杜培军，盛业华.高光谱遥感数据光谱特征提取算法与分类研究[J].计算机应用研究，2008,25(2)：390-394.

[7] 刘峰，龚健雅.一种基于多特征的高光谱遥感图像分类方法[J].地理与地理信息科学，2009,25(3)：19-22.

[8] JAIN A K,DUIN R,MAO J C.Statistical pattern recognition:A review[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,20(1):4-37.

[9] KRUSE F A,LEFKPFF A B,BOARDMAN J W,et al.The Spectral Mapping Processing System(SIPS)：Interactive visualization and analysis of imaging spectrometer data[J].Remote Sensing of Environment,1993,44(2-3):145-163.

[10] 樊彦国，李翔宇，张磊，等.基于多波段分析的无阈值自动光谱角制图分类法[J].地理与地理信息科学，2010,26(2)：38-41.

[11] VANDERMEEE F,BAKKER W.Cross correlogram spectral matching:Application to surface mineralogical mapping by using AVIRIS data from Cuprite,Nevada[J].Remote Sensing of Environment,1997,61(3):371-382.

[12] 李希灿，王静，李玉环，等.基于模糊集分析的土壤质量指标高光谱反演[J].地理与地理信息科学，2008，24(4)：25-28.

[13] 顾晓鹤，王堃，潘瑜春，等.基于HJ1AHSI超光谱影像的耕地有机质遥感定量反演[J].地理与地理信息科学，2011,27(6)：69-73.

[14] CHANG C I.An information-theoretic approach to spectral variability,similarity,and discrimination for hyperspectral imagery analysis[J].IEEE Transactions on Information Theory,2000,46(5):1927-1932.

[15] 安斌，陈书海，严卫东.SAM法在多光谱图像分类中的应用[J].中国体视学与图像分析，2005(1)：55-60.

[16] 孔祥兵，舒宁，陶建斌.一种基于多特征融合的新型光谱相似性测度[J].光谱学与光谱分析，2011(8)：2166-2170.

[17] 白继伟，赵永超，张兵，等.基于包络线消除的高光谱图像分类方法研究[J].计算机工程与应用，2003,39(13)：88-90.

Spectral Matching Classification Approach and Experiment Combined with Spectral Angle Cosine and Spectral Correlation Coefficient

WEI Xiang-po,YU Xu-chu,FU Qiong-ying,LIU Bing，XUE Zhi-xiang

(InformationEngineeringUniversity,Zhengzhou450001,China)

Spectral similarity measure is the criterion for spectral matching classification of hyperspectral imagery.Single spectral similarity measure can not involve multiple features of spectral curves,such as shape feature and radiation feature,so classification accuracy is low when single spectral similarity measure is used to spectral matching classification of hyperspectral imagery.The study found a combination of two or more similarity measures could effectively improve the accuracy of spectral matching classification.On the basis of the measures of spectral angle cosine and spectral correlation coefficient,spectral angle cosine-spectral correlation coefficient measure was obtained by way of the arithmetic mean of the combination.By using spectral angle cosine-spectral correlation coefficient measure to spectral matching classification,spectral matching classification approach combined with spectral angle cosine and spectral correlation coefficient was achieved.According to the approach,spectral matching classification process based on spectral angle cosine-spectral correlation coefficient measure was proposed.Classification of ROSIS and OMIS hyperspectral imagery in two experiments showed that,compared with the two separated measures,a higher overall classification accuracy could be obtained when spectral angle cosine-spectral correlation coefficient measure was used to spectral matching classification,and there was also an improvement in single-object classification to some extent.

hyperspectral imagery;spectral angle cosine-spectral correlation coefficient measure;classification;accuracy

2015-12-15；

2016-02-26

地理信息工程国家重点实验室开放研究基金项目(SKLGIE2015-M-3-1、SKLGIE2015-M-3-2)

魏祥坡(1991-)，男，博士研究生，主要研究方向为高光谱影像处理与分析。E-mail:13526635671@163.com

10.3969/j.issn.1672-0504.2016.03.006

TP75

A

1672-0504(2016)03-0029-05