环氧树脂材料中电磁辐射与裂纹动力的关系

S.O.Gade　U.Weiss　M.A.Peter　M.G.R.Sause



环氧树脂材料中电磁辐射与裂纹动力的关系

S.O.GadeU.WeissM.A.PeterM.G.R.Sause

摘要应用电磁辐射(EME)和声发射(AE)信号检测研究了机械应力加载条件下脆性、介电性材料的断裂。对环氧树脂样品采用3点弯曲实验装置施加应力使之破裂，同时监测破裂引起的电磁辐射和声发射信号。本次研究的重点是裂纹面的走向及距离对检测到的电磁辐射信号的影响。由于采用的电磁辐射传感器是电容式传感器，我们利用人工检测源测试了传感器、连接的放大器、数据采集卡以及内置带通滤波器的系统响应特征。基于在破裂面位置上模拟的表面电荷密度，我们提出了一种电磁辐射信号的源。将电磁辐射源的有限元方法模拟结果与实验结果进行比较，显示出较好的一致性。实验结果显示辐射出的电磁场优势方向明显，检测到的信号幅值显著依赖于信号源到传感器的距离，并发现测量链对检测到的电磁信号带宽具有显著影响。进一步研究表明电磁信号由3部分构成，分别产生于不同机制，即裂纹生长过程中电荷的分离和弛豫，以及带电裂纹面的振动。

关键词电磁辐射声发射破裂环氧树脂传递函数有限元模拟

0引言

不同材料在破裂过程中产生电磁场的现象已经被研究了几十年，几乎在所有材料和各种破裂机制中都发现过电磁辐射[1—9]。对电磁辐射信号的探测和分析有助于理解裂纹形成的复杂过程，而当与其他无损检测(NDT)方法，例如对裂纹引起的声发射信号的检测方法联合使用时尤其有用。对电磁辐射的来源问题存在许多理论解释，然而针对不同材料和不同破裂模型，有关辐射场起源的解释是不同的。即使对于经过几十年研究的材料而言，对电磁辐射的来源问题依然争论不休。Frid等[2]对现有模型进行了全面回顾，认为其缺乏一致性，且与最近的实验结果存在矛盾。一些作者将产生电磁辐射的动力机制归因于裂纹面的机械振动[1，3]，相比之下，Frid等和Rabinovitch等建议以电荷表面震荡波的形式来描述电磁辐射现象[2，4，10]。已经提出的模型和实验结果之间依然存在矛盾，例如围绕剪切裂纹扩展中出现的电磁辐射现象等。此外，对其他来源比如电介质的惯性和四极极化等机理也进行了探讨[14]。

对介质破裂过程中电磁辐射信号的探测为我们监测裂纹的初始发育和扩展过程提供了一种可能。根据文献[8]，探测到的信号是裂纹面相对传感器走向的函数。而且，信号可能包含源的时空特征信息[2]。

有多种不同的测量技术可用于探测电磁辐射，根据采用的传感器类型可分为电偶极子和磁偶极子两类[15]，后一类包括环形天线、线圈等感应式传感器，用以观测磁场分量。虽然已尝试了提高感应式传感器的频率特征，可此类传感器仍然在响应频域表现出很强的共振[16]。电容式传感器诸如电容器或天线等用于测量电场分量，此类传感器在较宽的频率范围内显示出相对平坦的响应特征[17]。Partridge[18]对电容式探头做了理论性综述。电容式探头可作为电位传感器用于观测电场，并不会对电场产生明显的干扰[19]。附加了测量电路的电容式传感器是观测伴随材料破裂产生的电磁场的常用工具[20]。

脆性材料破裂时几乎不产生或完全没有塑性形变。裂纹的扩展是不稳定的，通常会导致脆性破坏。对于Ⅰ型破裂，裂纹面沿x方向的位移主要产生于yz平面的垂直方向(图1)。当裂纹沿着z轴方向扩展时，分子键断裂并且在裂纹面出现电荷，从而导致了非对称的电荷分离，但是其原因尚未完全得到解释[12]。必须指出的是，一些学者对这种对称的破坏提出了质疑[2，4，21]。然而在一些介电性固体中有类似的效应[22]。所得电荷分布的时间特征与裂纹尖端的扩展速度有关。因此，恒定的裂纹扩展速度会导致电荷密度线性上升，分离的电荷将以一定的弛豫时间常数重新结合，该常数取决于材料的介电性和裂纹的几何形状。这两种效应的组合导致了由裂纹扩展过程引起的电荷瞬时增加以及随后因电荷弛豫促成的降低效果。电荷除产生在裂纹尖端外，裂纹面上的电荷只要存在，就会与裂纹面一起运动。

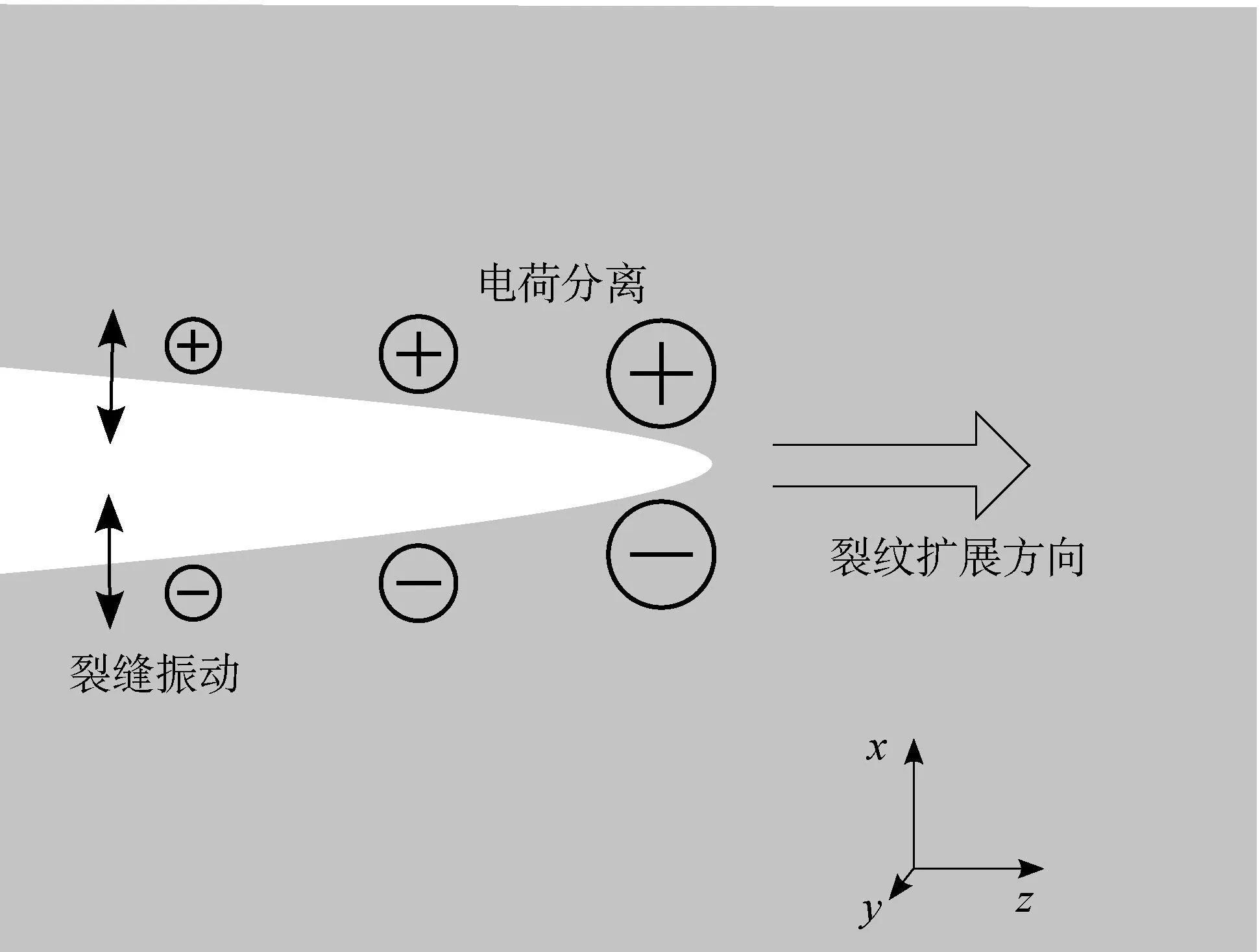
图1　Ⅰ型破裂的基本模型。基于裂纹扩展和伴随的电荷失衡，残留电荷在裂纹面随裂纹壁的振动而运动(原图为彩色图——译注)

裂纹的形成和生成裂纹壁的振动伴随有声波的产生，这种现象通常被称为声发射。这种声波的频率通常在超声波频率范围内。对声发射信号的探测和分析普遍应用在固体材料的破裂研究之中。压电式传感器能够探测得的最小振幅可达2.5×10-14m[23]，特制的宽频带传感器可以在感兴趣的频率范围内保持相对平坦的频率响应[24]。

对于计算复杂的物理系统和无法求得解析解的问题，数值模拟方法已经被证实是一个强有力的工具。通过应用适当的物理方程和关注模拟的物理内容，这种研究方法有助于增进我们对被模拟现象的理解。有限元法(FEM)是适用于解决多种物理问题的数值技术，可能进行模拟的现象有：裂纹生长[25，26]，声发射源[27]，声波在各向同性和各向异性材料中的传播[28，29]，甚至声发射传感器接收信号的传播等[30]。

有限元法建模用于解决各种电动力问题已有几十年[31，32]，但据作者所知，到目前为止尚未开展过对破裂所致电磁辐射现象的数值模拟研究。

本文介绍了一种方法，用于分析在脆性、介电性材料破裂过程中产生的电磁辐射信号。实验中使用了检测信号源，研究了所采用的电容式传感器系统和测量链对不同检测信号的影响，为此建立了一套实验装置，用来诱导环氧树脂样品产生破裂并探测随之出现的电磁和声发射信号。裂纹产生于既定的方向并且呈现为可重复的电磁辐射信号源，因此可以分析其他因素的影响，比如信号源到传感器的距离、破裂面与电容式传感器平面之间的夹角等。将记录到的电磁辐射波形与各自对应的声发射信号进行了比较。此外，使用有限元模拟方法研究了辐射源的基本特征，并且量化了测量系统对所探测信号的影响。模拟实现了对实验场景的三维仿真，包括模型源、电磁辐射传感器和测量电子电路的特征。通过从实验数据得出的传递函数来考虑电路的影响。

1实验

1.1实验装置

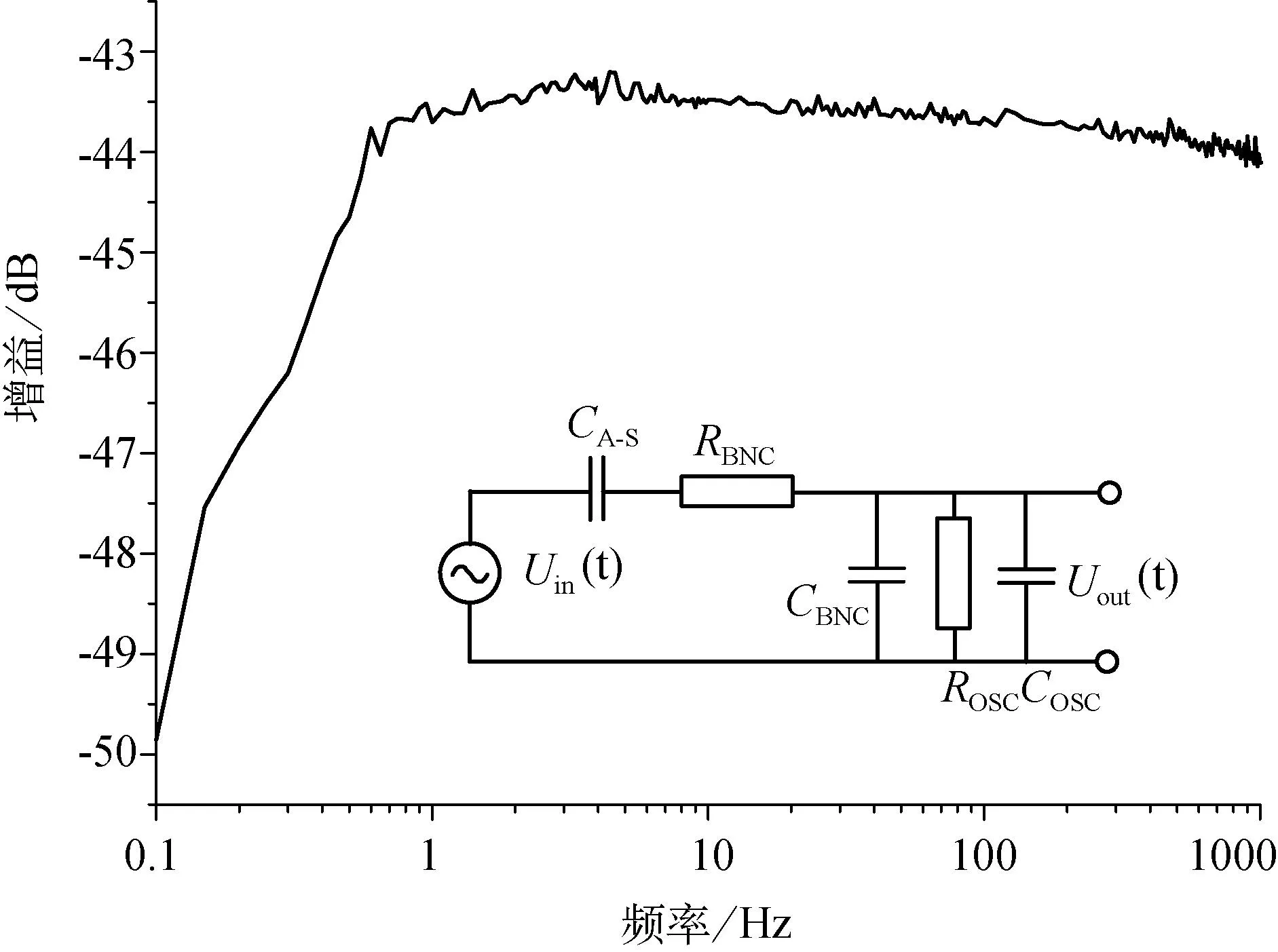
图2　天线—传感器系统的频率响应

图3　实验装置结构简图，包括万能试验机、固定装置、电磁屏蔽、电磁辐射和声发射传感器及测量设备(原图为彩色图——译注)

为了描述测试系统的特性，我们首先使用人工检测源进行测试实验。人工检测源由一个长5mm的小天线连接到Agilent 33210A任意波形信号发生器组成。小尺寸天线的共振频率在GHz范围内，因此认为其发射功率在低于1MHz的频段内是恒定不变的。由天线生成并发射特定的波形序列，用来模拟作为裂纹生长函数的虚拟电场的时间变化特征。天线和传感器被贴近放置，间距仅1mm，因此传感器板与检测源构成一个频率依赖于容抗的电容。

为了确定电抗的影响和验证此类测试源的适用性，使用任意波形发生器生成幅值1V，频率范围100Hz～1MHz的周期性电压信号。信号从天线发出，由传感器板接收。为消除前置放大器电路的可能影响，使用没有前置放大功能的示波器(GaGe CompuScope 14200)记录信号。根据输入频率设置示波器的采样率介于0.1～200MS/s之间。探测到的信号强度与输入信号的强度有关，图2所示为装置的等效电路。由于没有使用前置放大器，测量的电压在3～7mV范围内。在500Hz～1MHz范围内未发现谐振现象。由于电路本身构成了一个高通滤波器，导致500Hz以下频率的探测信号幅度下降。在等效电路中RBNC=10Ω，ROSC=1MΩ，CBNC=84pF，COSC=40pF，天线—传感器系统的实测电容为CA-S≈1pF，通过对等效电路的计算，结果显示了高通滤波特征和约为1kHz的截止频率。

测量电磁辐射信号的等效电路如图2所示，天线—传感器系统的电容要由传感器的电容来代替，后者的计算值CS≈0.5pF。输入阻抗和示波器的电阻将用相应的前置放大器的阻值来代替。输入电压代表了传感器板的电压。天线—传感器系统和传感器板的电容属于同一强度量级，但与电路的电容相比则显小。因此，甚少考虑天线对图2中传递函数和随后用到的测量链传递函数的影响。

研制了用来研究聚合物样品破裂时产生电磁辐射和声发射的实验装置(图3)。对样品单侧进行刻V形槽处理，并设计3点弯曲加载实验，以引导样品发生破裂。

制备了如图4所示相同尺寸的样品，为厚5mm的部分固化RTM6环氧树脂板。为了制备样品，在由双组分硅胶(Elastosil M 4601A/B)铸成的模具中充入黏性树脂并对其加热固化。对于80%交叉连接的树脂板以2K/min的加热和冷却速率进行固化处理，并在120℃保持30min，继之以135℃下保持140min[33]。交叉连接部分的温度由差示扫描测热法(DSC)确定[33]。然后，将树脂板切割成长25mm，宽b=5mm的长条状样品，并在长条中心预制深度3mm和宽度1mm的V形凹槽，于是样品中心部位的剩余厚度仅为2mm。

为了研究测得的电磁辐射信号强度与传感器板和电磁辐射源之间相对位置的关系，创造一个有清晰定向的破裂源大有裨益。我们预先刻槽的RTM6样品的破裂面方位角变化仅为φ≤5°。

图4　电磁传感器板的布置和RTM6样品及方位参数示意图(原图为彩色图——译注)

致弯夹具中采用了跨度为20mm的支撑和半径为1.5mm的加载针脚，夹具全部由不导电的材料制成，加载针脚由聚氯乙烯(PVC)加工制作，其余部分由有机玻璃(PMMA)制成。因为所有的导体会影响场的分布并因此降低传感器的灵敏度，所以选用绝缘材料很有必要[34]。因此，相对于样品而言，固定夹具显示出很高的柔度，夹具本身的柔度经测量为1.03μm/N，为弯曲实验中总柔度的17.5%。

使用通用试验机(Zwick ZT 5.0)以5mm/min的恒定速度施加机械载荷，对载荷的测量使用5kN的XforceHP压力传感器。

为了探测声学信号，将具有平坦频率响应的KRN型Glaser传感器固定在夹具上加载引脚以上部位(见图3)。对声发射信号采用2/4/6型无内部带通滤波功能的前置放大器进行20dB放大，然后以35dBAE的阈值进行触发式采集。信号由PCI-2系统记录(Mistras，软件：AEWin)，软件参数设置为峰值定义时间(PDT)10μs，撞击定义时间(HDT)80μs，撞击闭锁时间(HLT)300μs和1kHz～3MHz的带通滤波器(1kHz的4阶巴特沃思高通和3MHz的6阶巴特沃思低通的矩形窗函数)。

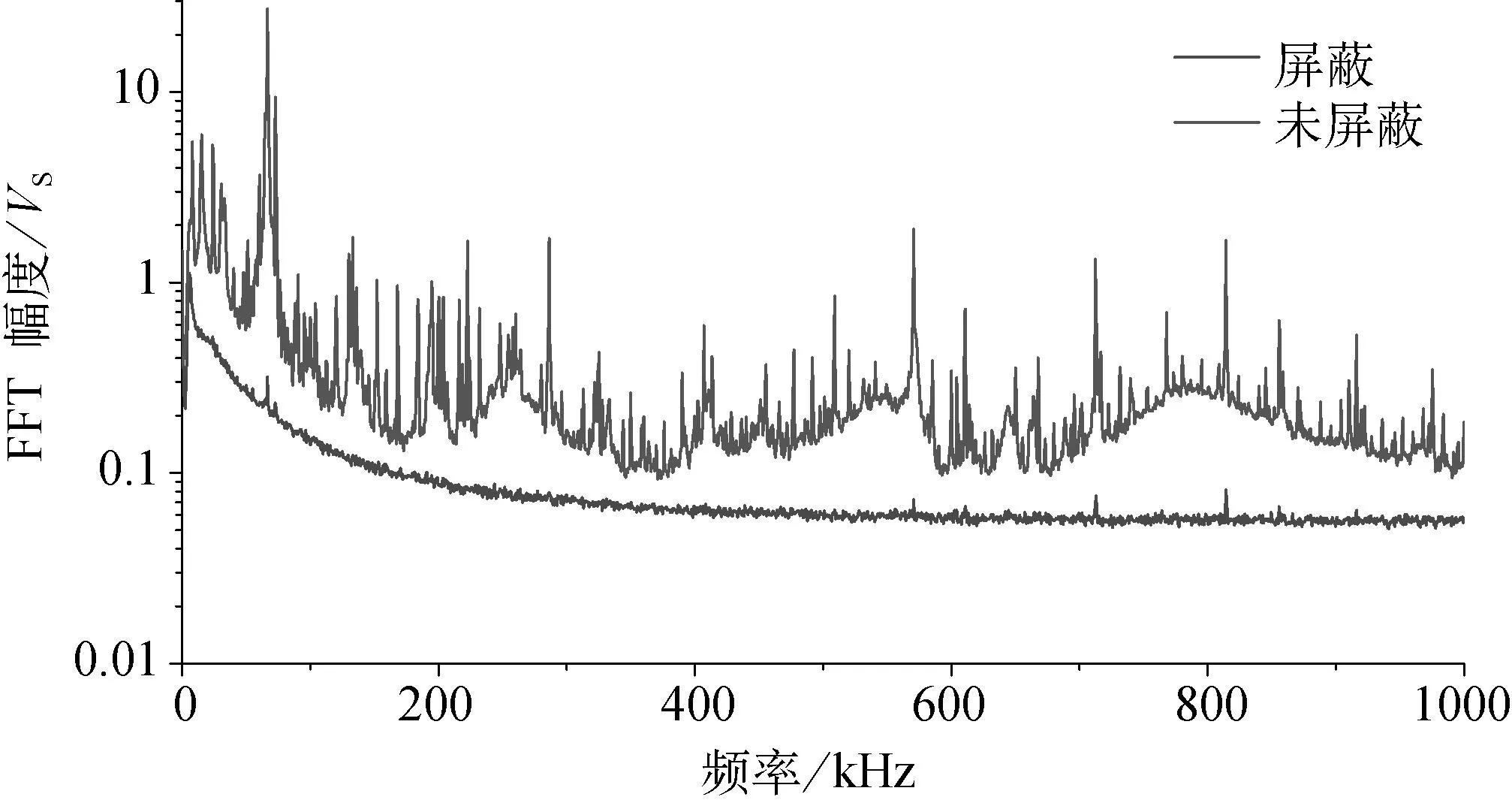
图5　有屏蔽和无屏蔽条件下测量的电磁噪声的频谱(原图为彩色图——译注)

对电磁信号的检测使用由两块小铜板电极(高6mm，宽8mm)构成的电容式传感器。其中一个铜板电极接地，另外一个连接2/4/6型无内部滤波的前置放大器。信号幅度放大倍数为40dB，同样采用PCI-2系统获取数字信号，使用的系统参数设置为触发阈值35dBAE，峰值定义时间50μs，撞击定义时间1 000μs，撞击闭锁时间1 000μs以及1kHz～3MHz带通滤波器。

最后对整个装置进行电磁噪声的屏蔽，并与万能试验机进行电绝缘。屏蔽罩为由3mm厚的铝板构成的接地铝盒，此类屏蔽罩在低频段显示出很好的屏蔽效果[35]。没有观察到缝隙泄漏对屏蔽结果的明显影响，为了载荷传输和线缆通过而在屏蔽罩上切割的孔洞并没有降低屏蔽效果，因为孔洞的尺寸远小于1MHz以下频率的电磁波波长，因此孔洞在低于截止频率时表现出波导特性。图5所示为分别在适当的屏蔽与未屏蔽条件下使用电容式传感器探测的电磁噪声信号的平均频谱分布。使用接地的屏蔽罩，可以将测量的电磁噪声幅度降低达一个量级。

为了模拟实验，测量了RTM6材料的介电性质，使用的仪器有频率响应Novocontrolα分析器(频率范围1Hz～10MHz)、自动平衡电桥Agilent 4980A(20Hz～2MHz)和阻抗/材料分析仪Agilent E4991A(1MHz～3GHz)。

1.2模拟

使用COMSOL Multiphysics软件的“电流”模块对实验装置进行模拟，该软件基于有限元方法，可以在模型中直接计算出实验装置附近电场中各自的电势。由于发生电场的波长远大于实验装置的尺寸，满足构成准静态场的条件(λ≫d)，所以选择将电场近似为准静态场。为了能够对比由模拟和实验方法得到的电磁信号，我们设计了基于实验装置的三维几何模型。图6所示为该模型的几何结构，由RTM6样品(橙色)、由绝缘材料制作的测试夹具装置(蓝色)、接地的屏蔽罩和其他导体部分(绿色)以及电磁辐射和声发射传感器(红色)组成。将实验装置的电容传感器左端、螺栓、声发射传感器以及屏蔽罩联合接地。对螺丝、传感器支架和声发射传感器部件的细节做了精细的几何简化，并不期望对计算电场造成明显的影响。

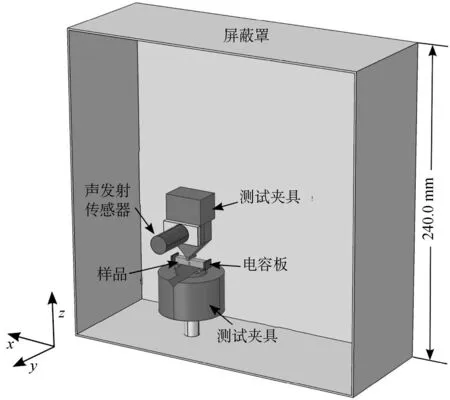
图6　仿真模型的三维几何结构。绿色表示接地的金属部分，蓝色表示绝缘部分，红色表示传感器，橙色表示RTM6样品(彩色图见网络版)

材料相对介电常数r电导率σ/S·m-1来源聚氯乙烯2.91e-14 [36,37]有机玻璃3.01e-14 [36,38]RTM64.125386.668e-10实测 空气1.000598e-15 [39,40]

相应的材料性质被指定给了代表模型绝缘部分的区域和空隙空间。表1中汇总了这些材料的介电性质。所有导电部分由适当的边界条件模拟，因此这些部分被认为是理想导体。地面边界条件被指定给所有接地部分，即屏蔽罩、声发射传感器和用来固定夹具的螺栓。传感器板使用浮动的电位边界条件模拟。

目前的模型中没有考虑样品破裂或者任何其他机械运动。将位于假设的破裂面上随时间变化的表面电荷以及对应产生的随时间变化的电场作为源函数使用，基于欧姆定律求解电流守恒问题并计算电压V：

(1)

(2)

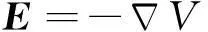
(3)

(4)

在类似实验中裂纹面的样品内部边界上定义边界电流源Qj：

(5)

我们使用二次拉格朗日元素法对空间进行离散，基于收敛研究我们选择对RTM6样品使用最大1mm分辨率的网格。对于构成探测电磁辐射信号的电容的两块小铜板，使用最大4mm分辨率的网格已经足够，这种分辨率也应用在固定装置和声发射传感器之上。其余的区域，即空气和被屏蔽、隔离的盒子，采用最大140mm分辨率的网格和最大1.5的单元增长率。这可以确保在样品与探测器之间的区域有足够的分辨率并降低自由度。通过广义α算法和5×10-7s的时间步长完成了随时间变化的计算。

Comsol模型设计中包括了除测量仪器信号处理部分之外的所有实验装置。传感器板作为感应电容的一部分，通过计算其表面的平均电势得到感兴趣的信号，并且认为模型附带电路的反馈可忽略不计。为了与实验获得的信号比较，测量电路的影响通过传递函数包括在内，传递函数由人工源测试实验获得：

(6)

式中，uWG(t)是波形发生器生成的输入信号，uMC(t)为由传感器系统测量的结果信号，F{ui(t)}是相应的经傅里叶变换后的信号。频率高于100kHz的成分从传递函数中被去除了，因其仅仅类似于系统中电路的本底噪声。与测量链其余部分的影响相比较而言，电磁辐射传感器的实测传感器特征(图2)的影响较小。

2结果与讨论

2.1人工信号源测试结果

为了提高对电磁辐射采集系统的了解，我们使用任意波形发生器驱动的人工检测源对其进行测试。在第一轮测试中遵循的基本假设为：信号的一部分来源于裂纹生长过程中的电荷分离；第二部分来源于随后的电荷弛豫。这两种部分的组合将在下文中被称为基信号。信号的第三部分是叠加的小振荡信号，推测其来源于带电裂纹面的振动。

由于电荷随着裂纹尖端而分离，并且在裂纹生长过程中不断积累，产生的电场将会增强，然后以一定的时间常数衰减。Ivanov等[41]发表了由破裂中的岩石引起的电场随时间变化特征的相关理论模型。

由于存在传导电流，给定的电荷分布会随时间衰减。RTM6样品裂纹面电荷的弛豫时间取决于RTM6样品及其邻近空气的介电性质。对于RTM6样品，我们测得σ=6.67×10-10Ω-1cm-1和εr=4.13。电荷的弛豫时间同样取决于带电表面及其周围介质的几何形态。并且介电性是与温度有关的函数，而裂纹尖端的温度远高于周围空间，因此弛豫时间在裂纹发育过程中随时间和位置而变化，之后则保持不变。对于均匀带电、分离了由不同材料组成的两个半空间的无限平面，表面电荷的弛豫时间可以通过公式计算得出：1/=1/2(1/1+1/2)，其中i=εi/σi，这种情况下，介于RTM6与空气之间的表面电荷的弛豫时间经计算为≈110ms。这种估算仅仅给出了实际时间常数的数量级，因为真实的裂纹面并不是无限平面。由于破裂过程远快于电荷弛豫，因此在此次估算中没有考虑表面温度的影响。

为了估算系统对具有不同弛豫时间的源信号的响应，我们生成了如图7上部所示的不同信号。这些测试信号类似于平滑阶跃函数，所有的测试信号显示出相同的上升特征，但是以不同的时间常数下降，在这两部分之间呈平滑过渡。这些信号发生的总长度为2ms，第一个信号不曾衰减(=∞)，其他两个信号分别以≈600和≈200μs衰减。考虑估算的RTM6样品的电荷弛豫时间，认为第一个信号可以代表实验情况。

由我们的电磁辐射传感器探测到的对应信号如图7下部所示，这样缓慢变化的电场仅有一小部分可以通过带通滤波器(1kHz高通4阶巴特沃思滤波器)。此外，现有的采集电路也具有频率相关的传输特征，会对探测信号产生影响。由此产生的信号类似于含有低于20kHz频率的缓慢振荡信号，结果表明这一振荡信号的主要部分来自于传感器系统对于测试信号中第一波上升的响应，这一波上升是连续增加的，持续时间约20μs。信号的测量采用反极性方法。只要弛豫时间足够长，检测信号后续的变化对于测量信号没有显著影响。测量信号上叠加了明显的本底噪声。

图7　( a，b，c上部)由任意波形发生器送入检测源的测试信号。每个具有相同的上升特征，但是衰减速率不同；(a，b，c下部)由现有传感器系统测量的结果信号，曲线形状由测试信号的上升特征主导(原图为彩色图——译注)

图8　(a)测试信号函数的振荡部分，由任意波形发生器产生的(上图)和由传感器系统实测的(下图)；(b)完整测试函数，包括基本部分和叠加振荡部分(上图)以及对应的实测信号(下图)(原图为彩色图——译注)

为了检测测量链对更高频率的响应，使用了频率80kHz的振荡信号(图8a上部)。假设这种振荡可以代表由带电裂纹面的振动产生的信号，它的上升和衰减次数取决于电荷的产生和弛豫以及裂纹面振动的衰减。之所以选择这种包络线的振荡信号是由于其在100μs内呈增加趋势，而后以100μs的时间常数衰减到0。图8a(下部)所示为传感器系统对振荡部分的响应，这部分实测信号的上升、衰减次数和振荡频率保持不变。试验信号和实测信号的极性正好相反。

图8b(上部)所示为基信号与振荡信号叠加成为测试信号的结果，选择1/200作为两部分的最大振幅比。图8b(下部)所示为完整试验信号的实测电压信号，实测信号清晰地展示了基信号的上升与所叠加的80kHz振动部分所引起的系统响应。总之，使用了测试信号源的实验结果清楚地说明目前的测量链不能探测到1kHz频率以下的信号。此外，如果快速振荡信号叠加在缓慢变化场之上，就会几乎原封不动地被检测出来。

2.2弯曲实验结果

当外部加载超过抗压强度时，样品会发生完全破裂。每个样品破裂都产生一个需要解释的电磁辐射和声发射信号。这些信号由裂纹扩展过程中产生的许多独立信号组成，这些独立信号在时间和空间关系上都接近破裂源，并且因此分别合成为一个电磁辐射和一个声发射信号。裂纹动力受到样品不同部位应力的影响，弯曲实验中大致有拉张区与压缩区两个主要的区域。因此，破裂过程由许多独立步骤组成，各自具有不同特征。图9所示为样品经过裂纹扩展后的破裂面图像。在这个例子中，裂纹的扩展开始于预制切口边缘的一个高张力点，可见辐射状裂痕标志线平行于裂纹扩展的方向，长条状裂痕指示裂纹分支发生的区域和加速、不稳定的裂纹扩展。上半部分(压缩区域)平滑如镜，具有平直的、肋骨状横向裂纹(沃尔纳线)，这表明较慢的破裂速度和扩展方向垂直于这些线。由于裂纹面大多是平滑的，裂纹面积可以用它的高度和宽度来近似确定。所得裂纹面几乎平行于y-z平面，最大偏差角为5°。

图10所示为用电磁和声发射传感器从一个代表性样品中测量的信号。声发射信号受到所用传感器和实验装置的影响。由于样品太小而不能直接把声发射传感器贴附于样品表面，所以将声发射传感器贴附在加载压头之上的固定装置表面。沿着从裂纹到传感器的传播路径，声波的传播会受到传输材料中阻尼、散射及几何形状边界反射的影响。

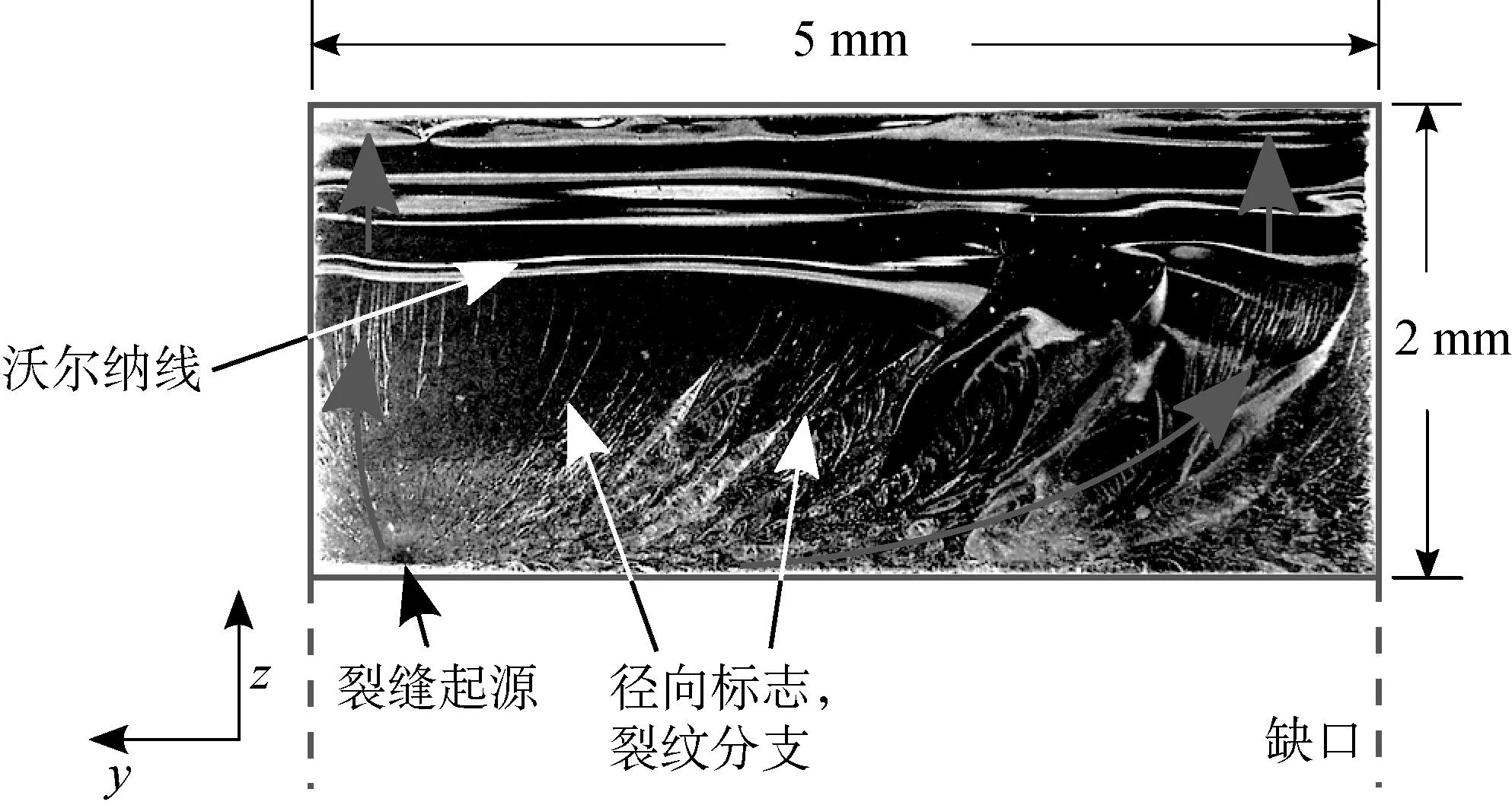
图9　RTM6样品裂纹区域的显微图像，标注了裂纹尺寸参数。红色箭头指示裂纹从预制切口的一点开始扩展，可见两类不同的裂纹扩展区域：一类是开始于裂纹发育原点的布满径向标志的粗糙区域，另一类是位于裂纹面上半部具有肋骨状条纹的平滑区域(原图为彩色图——译注)

图10　(a)从一个样品裂纹中得到的一对典型的电磁和声发射信号；(b)经过20～100kHz带通滤波的相同信号(原图为彩色图——译注)

图11　(a)典型电磁信号和电磁噪声信号(蓝色)频谱及对比(原图为彩色图——译注)；(b)40～42kHz带通滤波信号；(c)65～85kHz带通滤波信号

根据模拟结果和我们利用信号源所做的测试，电磁信号由几种成分叠加而成。主要部分为低频振荡信号(如图10a上部所示)。这个部分与裂纹扩展过程中的电荷分离有关。基于我们利用信号源所做的实验，这一部分是测量链对于场的非线性上升过程最初20μs的系统响应。较高频率和较小幅值的振荡信号叠加在此基信号之上，推测这部分信号是由裂纹生成和扩展过程中及之后的裂纹面振动引起的。与基信号相比，这些振荡信号的振幅比显得比实际值大许多。图11a显示了典型电磁辐射信号的频谱，为了比较，同时显示了典型的噪声信号。基信号部分的频率范围从1kHz～20kHz左右，显然还存在另两种成分，在41.2kHz的尖锐峰值和中心频率在76kHz的宽缓峰值。这两种成分的波形分别用40～42kHz和65～85kHz的带通滤波器滤出并显示在图11(b)和11(c)中。这两种信号都存在类似的周期性波动和清楚的上升和衰减特征，推测其由裂纹壁的振动产生。

将电磁辐射信号与声发射信号进行比较时(图10)，必须要考虑声发射频率会受到样品几何形状和从源到传感器的传播路径的影响[8，42]。此外，裂纹尖端扩展和裂纹面振动会产生电磁辐射和声发射信号，而电荷弛豫只会产生电磁辐射信号。对电磁辐射信号进行20～100kHz带通滤波后，可以去除大部分的基信号和隐含的噪声，而将同样的滤波器应用到声发射信号以后，只能部分去除杂散信号。然而，滤波后的电磁辐射和声发射信号在频率成分、上升和衰减时间方面仍然不同。

为了研究当前传感器系统以及裂纹产生与扩展过程中产生的辐射场的特征，我们做了一些弯曲实验。变化的参数包括从样品中心到电磁辐射传感器的距离d，裂纹面法线与传感器板法线之间的夹角φ。为了保证统计显著性，在每个测量点都试验了6～8个样品。通过使用公式(7)计算绝对能量，对信号进行了逐个分析。其中ZM=10kΩ是所用测量仪器的输入阻抗：

(7)

将每一测量点计算得到的能量值进行平均，产生一个数据点。虽然制备的样品尽量相同并被小心地放置在实验装置上，仔细调整方位，但是电磁辐射和声发射在信号强度上仍然分布离散。这导致计算数据的标准偏差较大，电磁辐射和声发射信号的标准偏差处于同一数量级。因此，将这种高标准偏差归因于破裂过程的复杂性，而不是信号的检测过程。

2.2.1探测角度的影响

当传感器方位保持不变时，将致弯夹具旋转并保持与z轴方向正交。通过这种方式裂纹面法线与传感器板法线之间的夹角将发生系统变化。为了研究这一角度对电磁辐射信号强度的影响，以10°为步长将角度从0°(平行)改变到90°(垂直)，传感器的距离d(见图4)保持在14mm不变。对于记录的电磁辐射信号，将其绝对能量作了量化，并对信号进行了20～100kHz的带通滤波，去除了基信号和大部分的隐含噪声，只留下了波的振荡部分，同样对滤波后的信号能量也作了量化。结果见图12。

从两种部分的信号中都可以看到信号能量与探测角度之间有清楚的对应关系。当裂纹面与传感器板平行时探测到的信号能量最强，而随着角度的增大，信号能量则显著减弱，这表明场的分布具有定向特征。

对于信号的不同部分，表现出的角度方向性不同。图12所示为实测信号的计算能量，包含基信号部分和振荡信号部分，信号能量由基信号部分主导。基信号产生于裂纹生长过程中的电荷分离，显示出某种类型的偶极子特征，因为带有极性相反电荷的裂纹两侧表面将产生一个偶极矩，方向平行于裂纹面的法线。探测到的信号能量与振荡部分的能量相比显示了更强的角度相关性。只有当角度增加到40°时，探测到的能量才能显著超过噪声水平，在0°时探测到的能量最大。在φ=10°时的信号能量下降到φ=0°时能量的53%。

信号的振荡部分由裂纹面的振动所产生。当假设这种振动垂直于裂纹面时，即具有强的指向性时，相应的可以期待探测的信号具有角度相关性。实际测量的信号形态显得比预期的简单偶极子特征更加复杂。对于点状偶极子，其电势与cos(φ)成比例，因此可以预期探测到的信号能量与cos2(φ)成比例(如图12b所示)，然而，探测到的信号能量只能部分满足这种期望，因为传感器不是点状的，即使对于φ=90°，传感器可能探测到其他角度的场分量。这可以用来解释小角度时探测到更强的能量，并且可以预期那时出现偶极子的特征。

由于声发射传感器的位置相对于夹具和样品在测试过程中都没有改变，所以探测到的声发射信号只是在标准差范围内离散。信号强度可以通过平均绝对能量614±466pJ进行估算。

2.2.2传感器距离的影响

样品尺寸的一个优势是能够在每一处定向观测中使电磁辐射传感器的位置紧靠裂纹。当电场源与探测器之间的距离增大时，所测信号强度随之减弱，推测原因为受几何路径传播的影响。另外，电场的空间特征取决于源的类型及其周边物质，例如场源附近导体的存在会影响电场分布。为了测量传感器系统对距离的敏感度，我们在源到传感器之间不同距离的条件下对电磁辐射信号进行了测量。从3个不同角度φ=0°，45°和90°分别对信号进行测量，并且对传感器板的距离进行了调整，从可能的最近距离一直远到信噪比对信号的探测构成阻碍的距离。对记录的信号和滤波(20～100kHz带通滤波)后的信号进行能量分析，图13中显示了能量计算的结果，其中图13(a)为完整信号的能量；图13(b)为信号中振荡部分的能量。

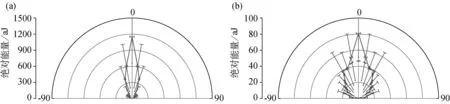
图12　信号性质随探测角度的变化。为了清楚起见，将数据在0°轴做了镜像。(a)完整信号的绝对能量随角度的变化；(b)信号振荡部分绝对能量随角度的变化，和成比例的cos2(φ)图(虚线)(原图为彩色图——译注)

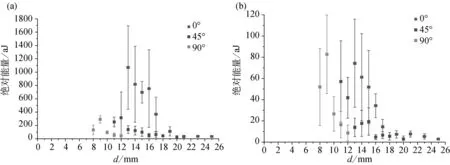
图13　(a)完整信号的绝对能量与源—传感器距离的关系；(b)信号中振荡部分的绝对能量与该距离的关系(原图为彩色图——译注)

正如所料，测得的能量随源—传感器距离的增加而减少，并在3个观测角度下全部如此。前一小节讨论结果表明，信号的不同部分表现出对角度的依赖性不同。而基信号和振荡信号对距离的依赖性则显得几乎相同，两部分的信号都只能在几毫米的距离内被探测到。绘图数据显示信号特征没有随距离d的明显变化，这可能是由于传感器位置相关的多种影响因素所致。主要效应预期来自于电场的空间特性，由偶极子产生的电位以1/d2系数降低，这将导致测量的信号能量以系数1/d4降低，过去还不曾观察到这种对距离的依赖。由于真正的电荷分布还不清楚，在破裂过程中也可能出现不同量级的多极矩，表现出不同类型的对距离的依赖性。此外，随着d的增加，电容板之间的距离随之增加，因此电容会减小。对于恒定的场强，电容越小，电容板之间获得的电压越高。另外一种效应可能比电容随距离增加的影响还要大，那就是实验装置中其他导电部分的影响。虽然固定装置采用绝缘材料制成，但一些其他元件不可避免地含有导电材料，其中最重要的是位于样品上方25mm处的声发射传感器。由于靠近源的所有导体都会影响传感器板上的电压[34]，这种影响在较大的传感器距离情况下变得更为显著。

对相应的声发射信号能量分析结果显示没有明显的上升和下降趋势，且认为声发射能量在其标准差范围内保持不变。当角度φ=0°时，绝对能量的平均值为11.2±1.8nJ。

2.3模拟结果

为了开发电磁辐射源模型，我们在数值模拟中将测试结果与人工测试源的结果相结合。对于随时间变化的电荷分布，在固定距离上的电势正比于电荷密度。因此，选择电荷密度的时间特征作为模型源，且正比于人工源实验中任意波形发生器产生的电压变化。由于仿真模型需要用电流源作为输入，我们使用相应实验中应用的测试函数的时间导数作为模型源Qj(t)=∂tρ(t)。图14(a)所示为使用的激发函数。对应的表面电荷密度类似于图14(b)所示的测试函数，由上升部分和振荡部分组成。有限元法模型包含了源和传感器之间的物理现象以及周边物质的影响。模拟结果为传感器表面的平均电位，并将其作为源电流的函数(图15)。

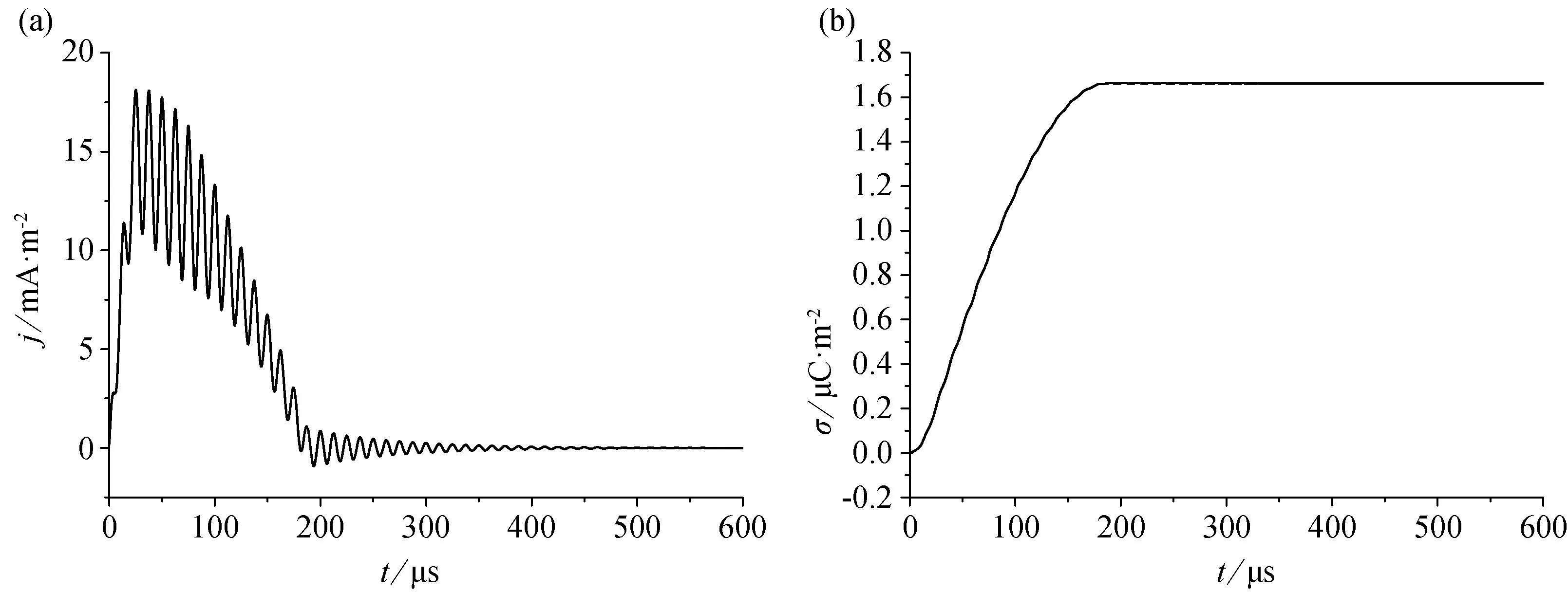
图14　(a)在模拟中作为电流源的表面电荷密度随时间的导数；(b)相应的表面电荷密度，由上升的基信号和振荡部分组成

计算出的电势与测试信号(图8b，上部)相同，将计算出的信号与系统的传递函数做卷积，以包含测量链的影响。输入的面电荷密度，最大值为1.663pC/mm2，产生的模拟信号与实验中源信号的幅度变化相匹配，见图16。

这表明这样的电荷分布可以产生类似于破裂实验中获得的电磁辐射信号。因此，我们提出的对于电磁辐射源的描述适用于描述实验中获得的信号。我们发现，对于固定的源—传感器距离，位于传感器位置上的电位与裂纹面的电荷成正比。模拟结果还表明所用的测量链对所探测的电磁辐射信号有实质影响。

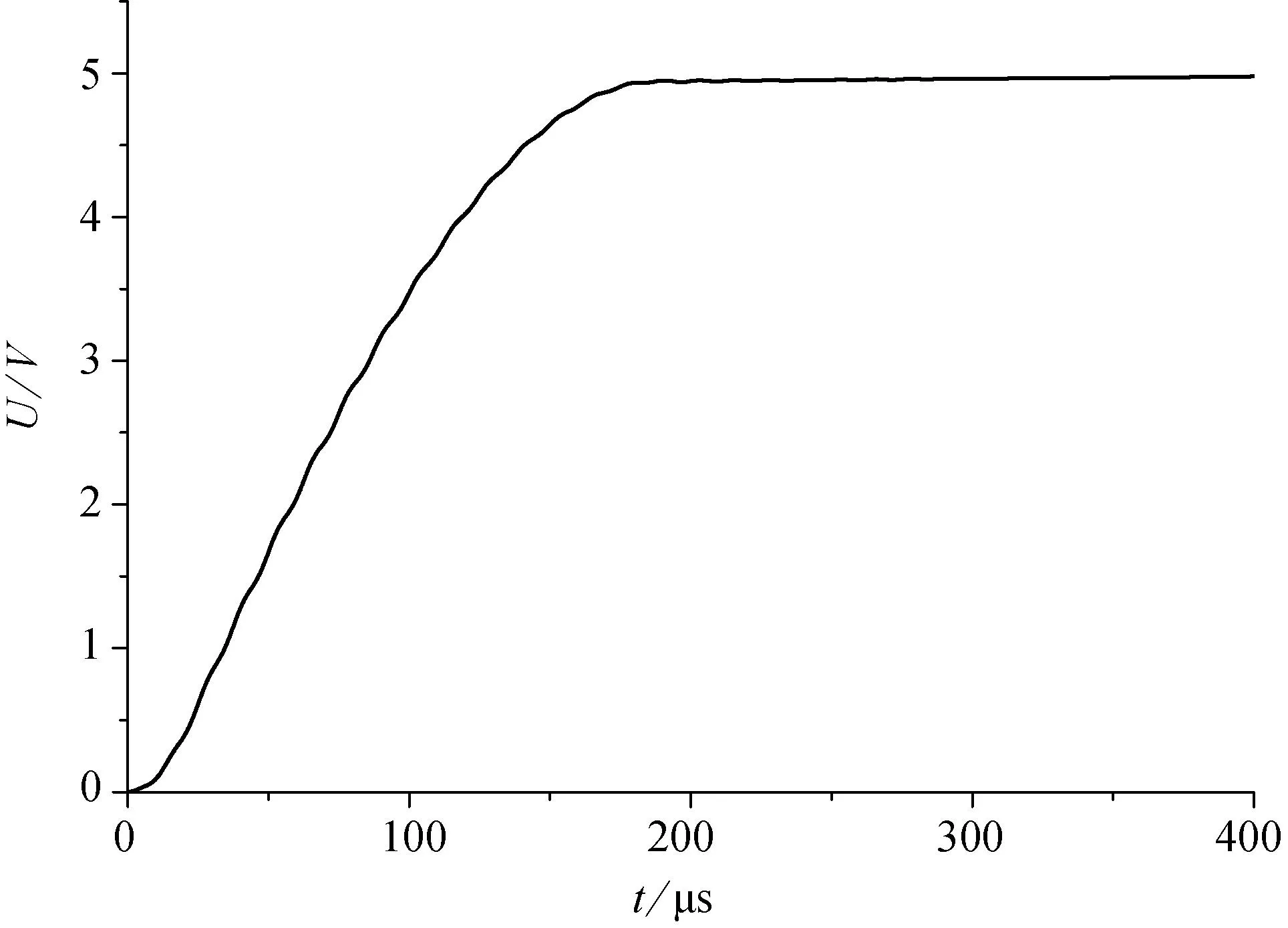
图15　传感器表面计算的电位

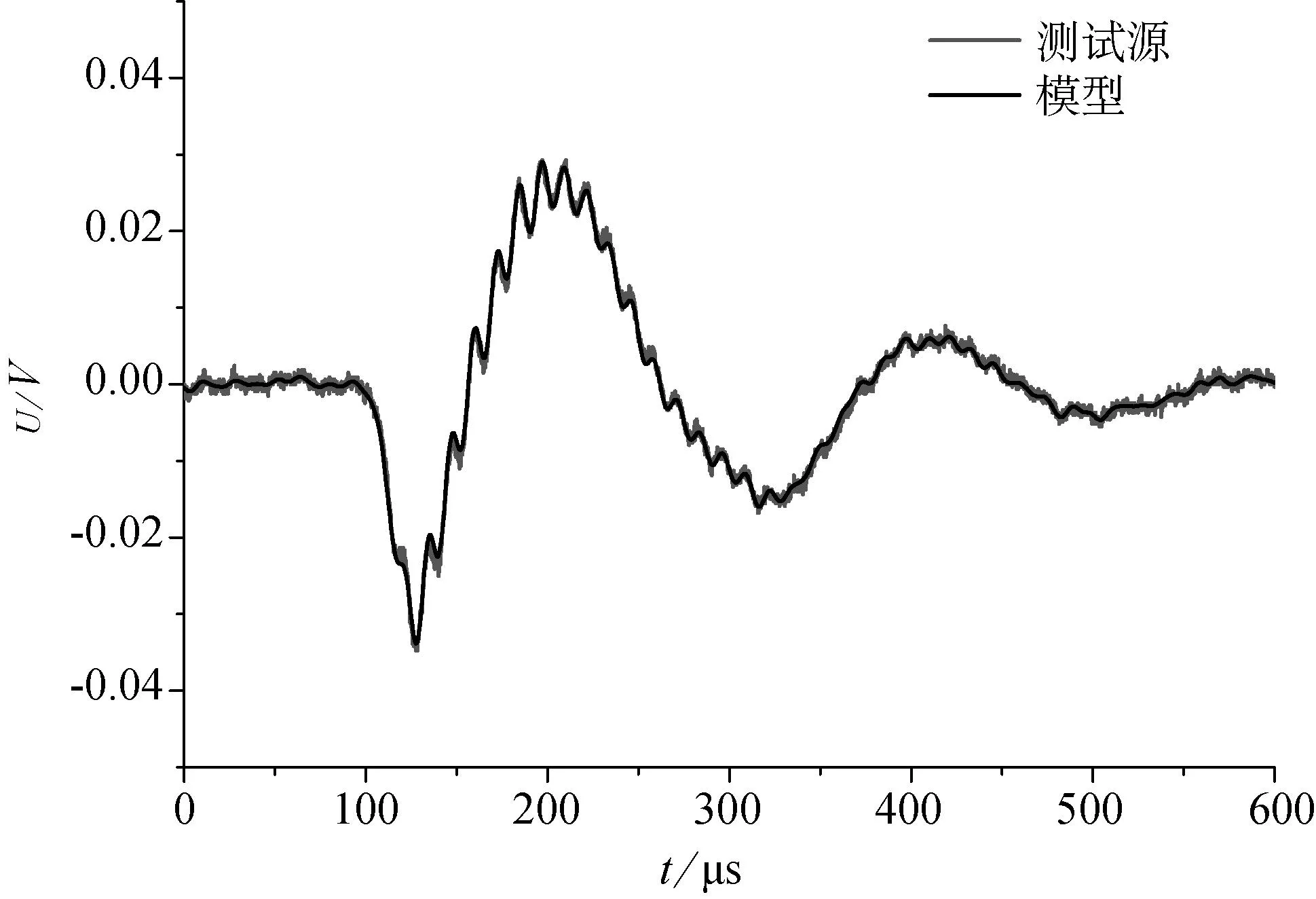
图16　计算波形与实测波形的比较(原图为彩色图——译注)

3结论

研究结果显示脆性介电性材料破裂过程中发射出的电磁辐射信号由3种不同部分组成。低频部分来源于裂纹生成和扩展过程中电荷不平衡的增加，它的特征取决于裂纹尖端位置随时间的演化。随后的电荷弛豫是所研究材料的介电性质的函数，但是鉴于目前采集系统的带宽限制，并没有探测到这部分信号。低频信号上叠加了小幅高频的振荡信号，与声发射信号的频率范围大致相同，认为这些振荡信号是由裂纹壁的振动引起的。

记录的电磁辐射信号强度主要取决于源—传感器的距离和传感器板与裂纹面之间的夹角。电磁辐射信号仅在几毫米的范围内能够探测到，且最强信号出现在传感器板平行于破裂面的情况下。

构建了随时间变化的表面电荷密度基本模型，利用该模型计算出的信号与实验中探测到的电磁辐射信号一致。电荷密度的时间特征模拟了裂纹面的电荷累积及其很小振幅的振荡，电荷的累积归因于扩展中的裂纹，小幅振荡反映了带电裂纹面的振动。

对于来自破裂过程的电磁辐射信号的产生和采集取得了重要认识。设想在不远的将来开展进一步的实验，并结合实际的裂纹动力过程强化模型，可以加深对基本物理现象的理解。

对电磁辐射适用性的测试已表明可作为一种有价值的无损检测方法，我们目前正专注于必要的步骤以便将这一技术发展成为一种无损检测方法。

参考文献

1.Yamada，I.，Masuda，K.，Mizutani，H.：Electromagneticandacousticemissionassociatedwithrockfracture.Phys.EarthPlanet.Int.57，157-68(1989)

2.Frid，V.，Rabinovitch，A.，Bahat，D.：Fractureinducedelectromagneticradiation.J.Phys.D36，1620-1628(2003)

3.Sedlak，P.，Sikula，J.，Lokajicek，T.，Mori，Y.：Acousticandelectromagneticemissionasatoolforcracklocalization.Meas.Sci.Technol.19，7(2008)

4.Lacidogna，G.，Carpinteri，A.，Manuello，A.，Du-rin，G.，Schiavi，A.，Niccolini，G.，Agosto，A.：Acousticandelectromagneticemissionsasprecursorphenomenainfailureprocesses.Strain47，144-152(2010)

5.Misra，A.，Prasad，R.C.，Chauhan，V.S.，Srilakshmi，B.：Atheoreticalmodelfortheelectromagneticradiationemissionduringplasticdeformationandcrackpropagationinmetallicmaterials.Int.J.Fract.2，99-121(2007)

6.Sklarczyk，C.，Winkler，S.，Thielicke，B.：Dieelek-trischeemissionbeimversagenvonfaserverbundwerkstoffenundihrenkomponenten.Mat.Wiss.Werkstofftech.27，559-566(1996)

7.Koktavy，P.，Pavelka，J.，Sikula，J.：Characterizationofacousticandelectromagneticemissionsources.Meas.Sci.Technol.15，973-977(2004)

8.Koktavy，P.：Experimentalstudyofelectromagneticemissionsignalsgeneratedbycrackgenerationincompositematerials.Meas.Sci.Technol.20，8(2009)

9.Koshevaya，S.，Grimalsky，V.，Makarets，N.，Kotsarenko，A.，Siquieros-Alatorre，J.，Perez-Enriquez，R.，Juarez-Romero，D.：Electromagneticemissionfrommagnetiteplatecrackingunderseismicprocesses.Adv.Geosci.14，25-28(2008)

10.Rabinovitch，A.，Frid，V.，Bahat，D.：Surfaceoscillations-Apossiblesourceoffractureinducedelectromagneticradiation.Tectonophysics431，15-21(2007)

11.Miroshnichencko，M.，Kuksenko，V.：Studyofelectromagneticpulsesininitiationofcracksinsoliddielectrics.Sov.Phys.SolidState22，1531-1533(1980)

12.O’Keefe，S.G.，Thiel，D.V.：AMechanismfortheproductionofelectromagneticradiationdu-ringthefractureofbrittlematerials.Phys.EarthPlanet.Inter.89，127-135(1995)

13.Rabinovitch，A.，Frid，V.，Bahat，D.，Goldbaum，J.：Fractureareacalculationfromelectromagneticradiationanditsuseinchalkfailureanalysis.Int.J.RockMech.Min.Sci.37，1149-1154(2000)

14.Laptukhov，A.I.：Generationofanelectromagneticfieldduringruptureofadielectric.RussianPhys.J.38，15-19(1995)

15.Baum，C.，Breen，E.，Giles，J.，O’Nelll，J.，So-wer，G.：Sensorsforelectromagneticpulsemea-surementsbothinsideandawayfromnuclearsourceregions.IEEEantennasPropag.26，22-35(1978)

16.Tumanski，S.：Inductioncoilsensors-areview.Meas.Sci.Technol.3，R31-R46(2007)

17.Kuechler，A.，Dams，J.，Dunz，T.，Schwab，A.：Kapazitivesensorenzurmessungtransienterelek-trischerfelderundspannungen.Arch.Elektrotech.68，335-344(1985)

18.PartridgeRE(1965)CapacitiveprobeE-fieldsensors.Sensorandsimulationnotes11 17pp.

19.Aydin，A.，Stiffell，P.B.，Prance，R.J.，Prance，H.：Ahighsensitivitycalibratedelectricfieldmeterbasedontheelectricpotentialsensor.Meas.Sci.Technol.21，5(2010)

20.Winkler，S.：Teardetectorformechanicalloadingtestsample-usescapacitivesensorcoupledviaimpedanceconvertertoelectronicevaluationcircuitpatentDE4004171，C2(1993)

21.Carpinteri，A.，Lacidogna，G.，Manuello，A.，Niccolini，G.，Schiavi，A.，Agosto，A.：Mechanicalandelectromagneticemissionsrelatedtostress-inducedcracks.Exp.Tech.3，53-64(2012)

22.Chakravarty，A.，Phillipson，T.E.：Triboluminescenceandthepotentialoffracturesurfaces.J.Phys.D11，2175-2180(2004)

23.Boltz，E.S.，Fortunko，C.M.，Hamstad，M.A.，Renken，M.C.：ReviewofProgressinQuantitativeNondestructiveEvaluation.PlenumPress，NewYork(1995)

24.Glaser，S.D.，Weiss，G.G.，Johnson，L.R.：Bodywavesrecordedinsideanelastichalf-spacebyanembedded，widebandvelocitysensor.J.Acoust.Soc.Am.3，1404-1412(1998)

25.Fish，J.，Nath，A.：Adaptiveandhierarchicalmodellingoffatiguecrackpropagation.Int.J.Numer.Meth.Eng.16，2825-2836(1993)

26.Hoppe，R.H.W.，Petrova，S.I.：Multi-scalemethodforthecrackprobleminmicrostructuralmaterials.Meth.Appl.Math.1，19(2010)

27.Sause，M.G.R.，Horn，S.：Simulationofacousticemissioninplanarcarbonfiberreinforcedplasticspecimens.J.Nondestruct.Eval.2，123-142(2010)

28.Prosser，W.H.，Hamstad，M.A.，Gary，J.，Ga-llagher，A.O.：Finiteelementandplatetheorymodelingofacousticemissionwaveforms.J.Nondestruct.Eval.3，83-90(1999)

29.Sause，M.G.R.，Hamstad，M.A.，Horn，S.：Finiteelementmodelingoflambwavepropagationinanisotropichybridmaterials.Compos.PartB53，249-257(2013)

30.Sause，M.G.R.，Hamstad，M.A.，Horn，S.：Finiteelementmodelingofconicalacousticemissionsensorsandcorrespondingexperiments.SensorActuat.A184，64-71(2012)

31.Coggon，J.H.：Electromagneticandelectricalmodelingbythefiniteelementmethod.Geophy-sics1，132-155(1971)

32.Jin，J.：Thefiniteelementmethodinelectromagnetics.Wiley，NewYork(2002)

33.Moosburger-Will，J.，Greisel，M.，Sause，M.G.R.，Horny，R.，Horn，S.：Influenceofpartialcross-linkingdegreeonbasicphysicalpropertiesofRTM6epoxyresin.J.Appl.Polym.Sci130，4338-4346(2013)

34.Ramo，S.：Currentsinducedbyelectronmotion.Proc.IRE9，584-585(1939)

35.Cooley，W.：Low-frequencyshieldingeffectivenessofnonuniformenclosures.IEEETrans.Electromagn.Compat.1，34-43(1968)

36.Lide，D.R.：CRCHandbookofChemistryandPhysics：AReady-referenceBookofChemicalandPhysicalData.CRCPress，BocaRaton(2003)

37.Ranicar，J.H.，Fleming，R.J.，Legge，C.A.：ElectricalconductivityinPoly(Vinylchloride).Aust.J.Phys.24，325-332(1971)

38.Adamec，V.，Mateová，E.：ElectricalconductivityofPMMAatlinearlyincreasingtemperatures.Polymer3，166-168(1975)

39.Hector，L.G.，Schultz，H.L.：Thedielectricconstantofairatradiofrequencies.Physics4，133(1936)

40.Pawar，S.D.，Murugavel，P.，Lal，D.M.：EffectofrelativehumidityandsealevelpressureonelectricalconductivityofairoverIndianOcean.J.Geophys.Res.114，8(2009)

41.Ivanov，V.V.，Egorov，P.V.，Kolpakova，L.A.，Pimonov，A.G.：Crackdynamicsandelectromagneticemissionbyloadedrockmasses：translatedfromfiziko-tekhnicheskieproblemyrazrabotkipoleznykhiskopaemykh.Sov.Min.Sci.24，20-27(1988)

42.Mori，Y.，Obata，Y.，Sikula，J.：Acouticandelectromagneticemissionfromcrackcreatedinrocksamplesunderdeformation.J.Acoust.Emiss.27，157-166(2009)

何明文(1986—)，男，中国地震局地球物理研究所硕士研究生，主要从事岩石加载实验电磁观测系统研究。E-mail：hemw989@163.com。

译 者 简 介

S.O.Gade，U.Weiss，M.A.Peter，M.G.R.Sause.2014.Relation of electromagnetic emission and crack dynamics in epoxy resin materials.JNondestructEval.33∶711-723.doi∶10.1007/s10921-014-0265-5

何明文 译.2016.环氧树脂材料中电磁辐射与裂纹动力的关系.世界地震译丛.47(2)∶160-176.doi∶10.16738/j.cnki.issn.1003-3238.201602006

中国地震局地球物理研究所何明文译；王红强校

中国地震局地球物理研究所吴何珍复校