带有地质和地形约束的加利福尼亚州VS30图

E.M.Thompson　D.J.Wald　C.B.Worden



带有地质和地形约束的加利福尼亚州VS30图

E.M.ThompsonD.J.WaldC.B.Worden

摘要许多地震工程应用工作中，场地响应由直到30m深度的时间平均剪切波速(VS30)的经验关系式估计。因此这些工作要么依赖于特定场地的VS30测量数据，要么依赖于全球、区域或局部尺度的VS30图。由于VS30测量数据稀少，所以我们通常需要代用值来估计未采样区域的VS30值。我们给出了一幅计及像地质、地形与特定场地VS30测量数据多源不同空间尺度观测约束的新加利福尼亚州VS30图。我们使用回归克里格(RK)地学统计方法结合这些约束预测VS30。对VS30趋势，我们以基于地质的VS30值开始，识别了两种清晰的介于地形梯度和地质VS30模型残差的趋势。一种趋势适用于深、细砂第四纪冲积层，而第二种趋势略强，适用于更新世沉积单元。回归克里格框架确保形成的加利福尼亚州图在局部上精细地反映了整个加利福尼亚州快速扩展的VS30数据库。我们比较了这种新制图方法与以前绘制的加利福尼亚州VS30图的精度。通过比较使用我们的新图和现有图VS30值的真实场景地震动区划图，我们也说明了地震动对新VS30图的敏感性。

0引言

在像地震动预测公式(GMPE)，建筑规范和地震危险性区划图等很多实际工作中，场地响应都由直到30m深度的时间平均剪切波速VS30的经验关系式来估计。为了绘制图件，我们需要诸如地表地质(Wills and Clahan，2006)，地形梯度(Wald and Allen，2007)或地貌(Yongetal，2012)的辅助信息(即，代用物)来估计未采样区域的VS30。这里，我们对加利福尼亚州采用了既利用地表地质又利用地形梯度的混合方法。我们使用回归克里格方法绘制VS30图(Thompsonetal，2010；Thompsonetal，2011)以保证所得到的加利福尼亚州的图件能在每一局部地点都能良好地反映迅速扩展的VS30测量数据库(例如，Yongetal，2013)。这里使用的VS30回归克里格制图方法类似于Worden等(2010)在地震动图中绘制地震动强度的制图方法，在地震动图中，空间的代用物(事件校正的地震动预测公式)在局部区域上精细地反应了仪器和宏观强度。

我们的长期目标是绘制包括给定地点现有最精确VS30估计值的全球VS30图。基于全球已有的地形的方法(Wald and Allen，2007；Allen and Wald，2009；Yongetal，2012)实现了完全的覆盖。然而，像加利福尼亚州、中国台湾和日本这些已被较详细研究过的区域，应该有更详细的VS30图和测量数据。Wills和Gutierrez(2008)绘制了基于地表地质单元的加利福尼亚州VS30均值和标准偏差图。随后，Wills和Gutierrez(2008)使用由地形坡度确定的因子修改了第四纪地质单元的VS30，对图进行了更新。目前，所有这些得到VS30估计图方法的一个局限性是，虽然最初来源于或受约束于VS30的观测值，但最终所得到的图上实际上忽视了测量位置上已知的VS30值。回归克里格方法解决了这个问题。这里，我们使用的是既有地质又有地形约束的回归克里格方法，但这种方法实际上是能够包含现有任何VS30预测因子组合的一个通用方法。例如，在缺乏足够详细地质资料成图的地方，人们可以使用仅用地形坡度的回归克里格方法。

回归克里格方法中的关键步骤是对均值的空间浮动定义函数(称为“趋势”)。定义趋势有很多可能的方法。最直观的选择是进行回归分析。回归分析中的方程函数形式包括地质单元、地形坡度及地形坡度与地质单元的交互作用项。使用这种方法的一个主要障碍是岩石单元中缺乏测量值，这个值在沉积单元中或许呈现出随地形坡度而不同的趋势。而岩石单元中的严重选择偏差又加剧了这个问题。这一偏差是由于岩石单元中成图的很多VS30测量数据实际被放在了至少部分下伏有沉积物的地方；再有就是地质图必须忽略小于某种特征尺度的特征，这种特征尺度取决于地图比例尺。在地质图上标为岩石单元的区域仍可包含小片的沉积物(如，沿河岸)。实际上，地震调查的区域通常不是所要求的地质单元的代表区域，而是易于进入开展工作的平坦区域。对日益广泛应用的非侵入面波反演方法更是这样，这些反演方法依赖用于捕捉约束30m及其以下速度结构的长周期面波的在长距离(数十到数百米)地表布置的地震仪台阵。结果是被划分为岩石单元地区的VS30测量数据通常并不代表图上所标的材料。比较起来，Wills和Clahan(2006)的图几乎仅依赖于不易产生同样采样偏差的井下测量数据，所以我们认为对于岩石单元，Wills和Clahan(2006)的图比我们使用加利福尼亚州当前已有数据统一回归能够制作的图更精确。

另一个合理的方法是分层模拟VS30，这种方法首先分析最广泛适用模型的残差。残差中的趋势可能明显是局部地质或地理区域的函数。这些趋势而后可以被用来在局部区域上改善更广泛适用的模型。例如Wald等(2011)的研究表明VS30与地形坡度的关系式在中国台湾和美国犹他州是类似的，但这一关系式出现了偏移(即，截距项不同)。相关的例子是Magistrale等(2012)绘制的美国大陆VS30图，它对年轻的湖相沉积明确表现出VS30与地形坡度之间不同的相关性。

然而，对于加利福尼亚州，因为前面讨论的岩石单元中的采样偏差问题，我们倾向用第三种方法，这种方法的基础或背景模型是Wills和Clahan(2006)(此后称WC06)图，在这个基础上，我们进行了残差分析，以确定作为地形坡度函数的VS30标度关系。

1数据

我们使用太平洋工程分析数据库(Walt Silva，书面通信，2011)和Yong等(2013)的VS30测量数据。为避开因WC06图有限空间精度和测量数据位置误差造成的场地分类错误，我们从数据库中去除了地质单元分类有疑问的VS30测量数据，即地质图在岩石单元上表示的是土层单元的VS30值，或相反。加利福尼亚州最终的数据库包含801个点。图1a绘出了这些点，且内插了VS30直方图；图1b给出了WC06图。

Allen和Wald(2009)的研究表明9角秒分辨率(即9c)地形梯度比30角秒分辨率(即30c)地形梯度描述地形或地质特征的效果更好。然而，Thompson和Wald(2012)发现中国台湾的测量数据和30角秒分辨率(约900m间距)地形梯度比9角秒分辨率(约270m间距)地形梯度相关得更好。粗糙的地形相关性为什么更好原因尚不清楚，但我们认为9角秒分辨率地形梯度可能反应了非地形特征(如，植被或建筑)。因此在我们的分析中使用了9角秒和30角秒的两种分辨率的地形梯度，这样来确定哪一种分辨率更适合加利福尼亚州地区。

2空间趋势

为把模型以方程表示，并且能明确地表述后面所提出的制图算法，我们对地质单元的WC06分组定义了一套指示变量：如果测量数据在地质单元g内，G等于1，否则等于0。这里g是WC06表1中列出的任何一个地质单元。这样，我们就可以把模型写成：

(1)

式中ci是gi地质单元WC06表1中所报告的VS30均值。我们把WC06模型的残差定义为下列比值：

(2)

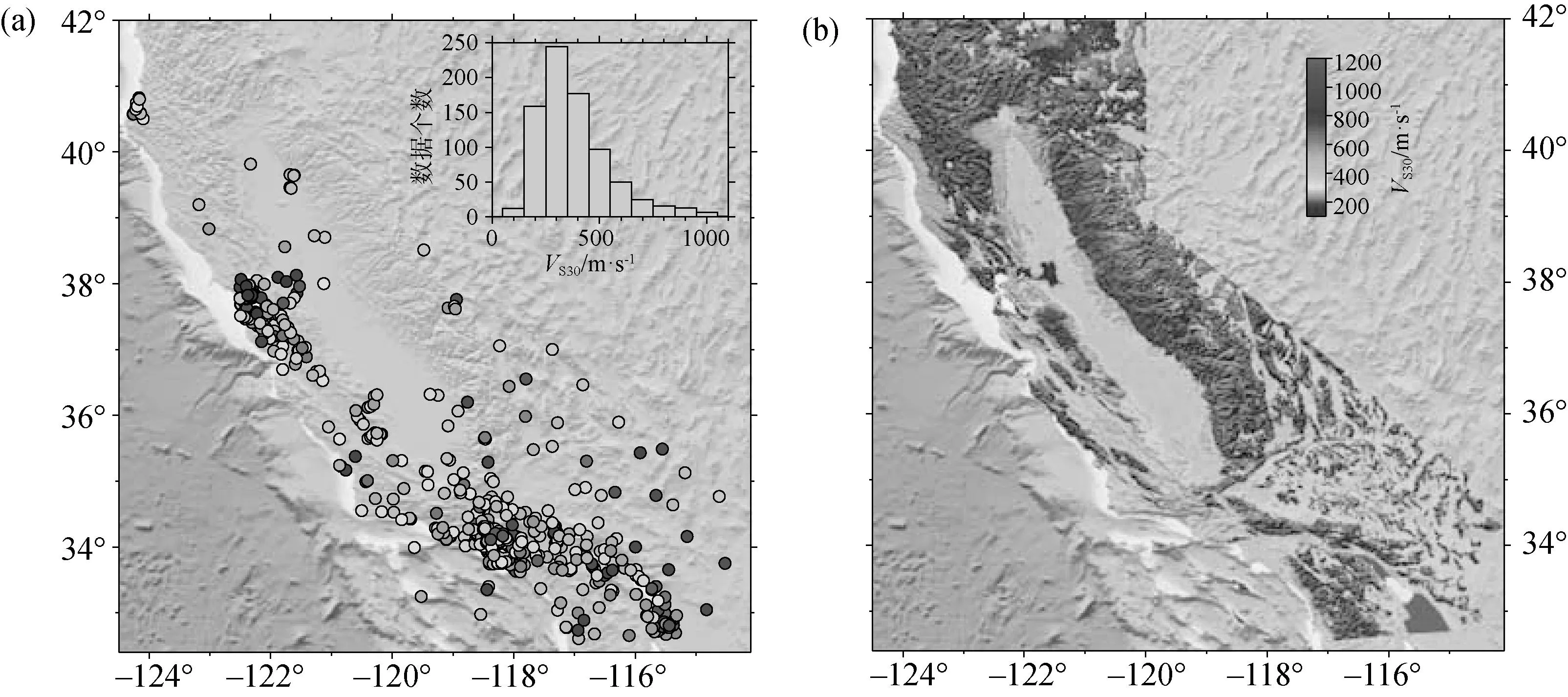
图1　(a)我们在分析中使用的加利福尼亚州VS30测量数据分布图及直方图(原图为彩色图——译注)；(b)Wills和Clahan(2006)的VS30地表地质模型

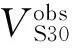
(3)

式中：

(4)

这里直线的系数(β0i，β1i)由最小二乘回归确定，其他系数(li，ui，ai和bi)则由数据的范围来确定以避免把趋势外推。选取这个函数形式以反应像图2中示出的rgeo的对数和地形坡度的对数之间的近似线性关系(即幂率关系)。表1给出了β0i和β1i的最小二乘估计值及其95%的置信区间，以及其他未经回归确定的系数。对于表1未列出的地质单元，式(4)等于1.0。因为式(3)包含了由地质和地形梯度所引起的变化，我们把它称为混合VS30模型。

图3比较了洛杉矶地区的WC06图和混合VS30模型。在118°W，33.8°N附近的沉积盆地内地形梯度效应是显而易见的，在这个地方，WC06模型是不变的(实橙色)，但混合模型显示出了VS30的变化(图中橙黄色的变化)。虽然这个单元的均值与WC06模型很类似，但在接近盆地边缘处混合模型的VS30变化得更快。其他区域上显示出了由地形梯度效应引起的空间分布广泛但幅度不大的VS30均值变化。例如，117.3°W，34.1°N附近的缓慢第四纪沉积物在WC06模型中较快，而在118.3°W，33.8°N附近的更新世单元上却一般较慢(虽然在混合模型中显然存在一条较快材料的带)。

表1　估算混合VS30模型需要的参数

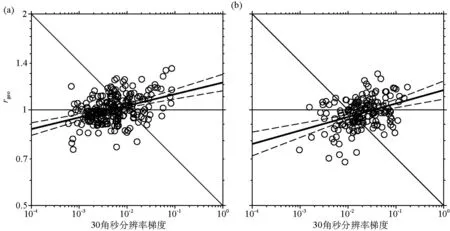
图2　随30角秒分辨率航天飞机雷达成像地形梯度变化的rgeo曲线图。(a)深/细砂第四纪冲积层的rgeo曲线图；(b)更新纪冲积层单元的rgeo曲线图。实线给出了最小二乘线性模型，虚线给出了95%的置信区间

3回归克里格

地质和地形坡度通常被称为VS30的“代用物”。在地学统计文献中更常用的另一个适当术语是“辅助信息”，人们已经研发了各种地学统计方法，来对那些局部解释所关心的直接测量数据的变量以及辅助信息(即“代用物”)进行编图。术语“克里格”包括很多不同利用数据中空间相关结构的地学统计插值方法，其中的一些结构也解释了各种辅助信息。采用Goovaerts(1997)的方法，我们可以把各种类型的克里格表述成：

(5)

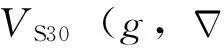
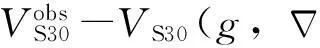
(6)

(7)

给出的Whittle-Matérn半变异函数模型。式中h是分离距离，σ2是偏基台值，是块金值，a是范围参数，ν是形状参数，Kv是ν阶的第二类变形贝塞尔函数，Γ是伽马函数。通过试错法我们选取了0.1作为ν值；剩余参数的最大似然估计值是σ2=9.26×10-3，=2.60×10-3，a=29.2。图4中标出了这些参数值，关于Whittle-Matérn模型更多的讨论见Thompson等(2010)的文章，关于根据半变异函数模型计算可参阅地学统计教科书(例如，Chilès and Delfiner，1999)。

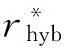
图3　洛杉矶地区VS30图的对比(原图为彩色图——译注)：(a)基于地表地质的WC06图；(b)混合地质/梯度的)图；(c)在(b)图上添加了观测数据

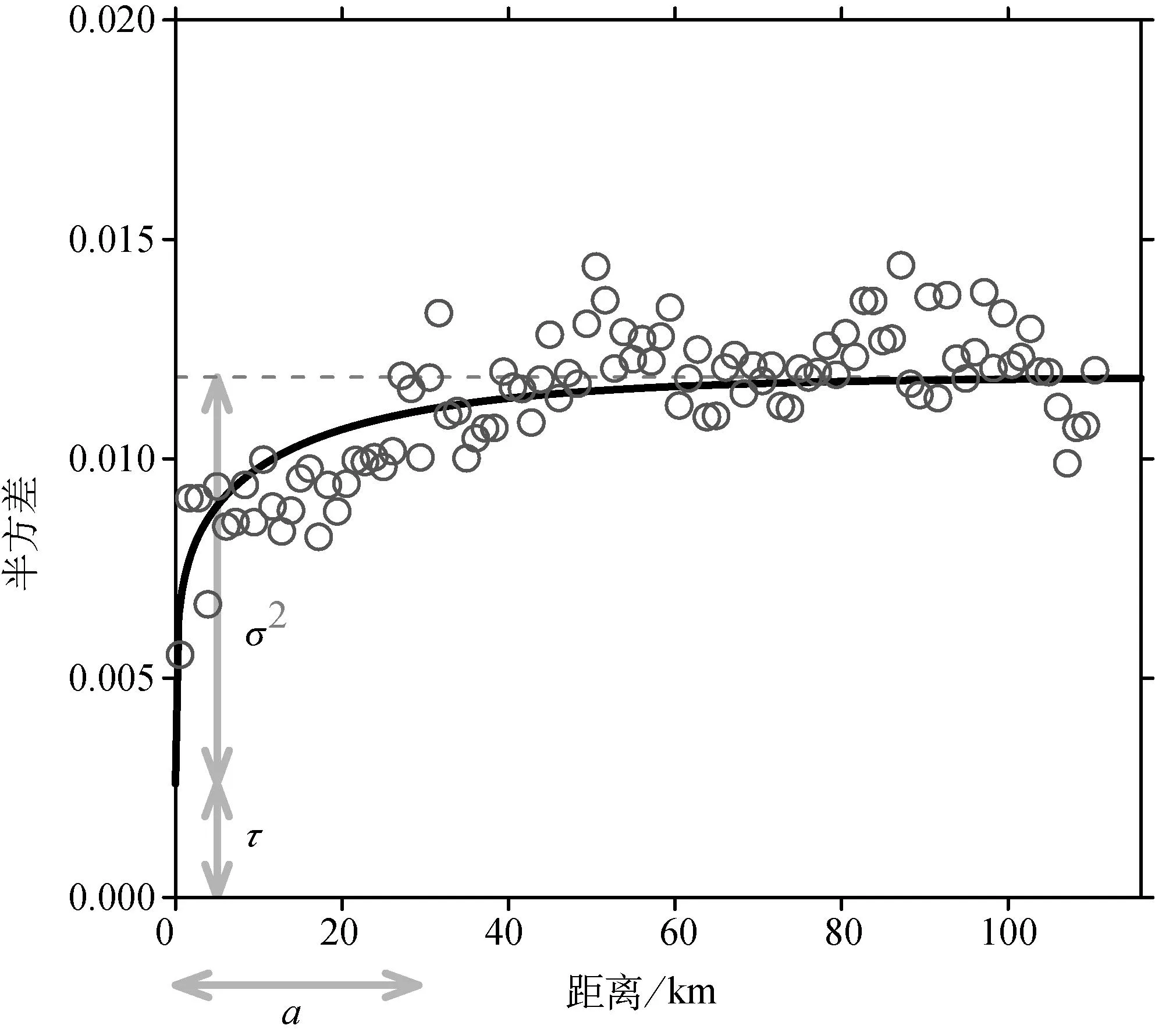
图4　rhyb的经验(点)和模型(线)半变异函数图。正文中定义了标识的参数：σ2是偏基台值，是块金值，a是范围参数

图5　(a)加利福尼亚州洛杉矶地区内插的混合模型残差)图(原图为彩色图——译注)；(b)加利福尼亚州洛杉矶地区最终回归克里格(RK)VS30图。这里趋势被定义为)。(a)中的蓝色区域表示实测数据一般低于Wills和Clahan(2006)分配值的区域，红色区域表示实测值一般高于Wills和Clahan(2006)分配值的区域

4不确定性

(8)

式中C(h)是协方差函数。协方差通过γ(h)=C(0)-C(h)与变差函数简单相关。由于没有解释回归步骤的不确定性，方程(8)给出了由数据估计的地形坡度趋势的地质单元内的最小不确定性，因为在这些地质单元内不考虑回归坡度的不确定性。图6示出了洛杉矶地区的误差标准偏差(σE，以10为底的对数为单位)。这张图清晰地说明了与VS30测量值附近位置有关的不确定性明显降低了。

在测量值位置几千米内的σE低至0.08，但在远处增加到0.11。此外，在人们最关心的区域，也就是人口密度最大的区域，不确定性一直都很小(约0.09)。

图6　洛杉矶地区以10为底的对数为单位的误差标准偏差(σE)图(原图为彩色图——译注)。它说明了降低了的与实测VS30值附近位置有关的不确定性

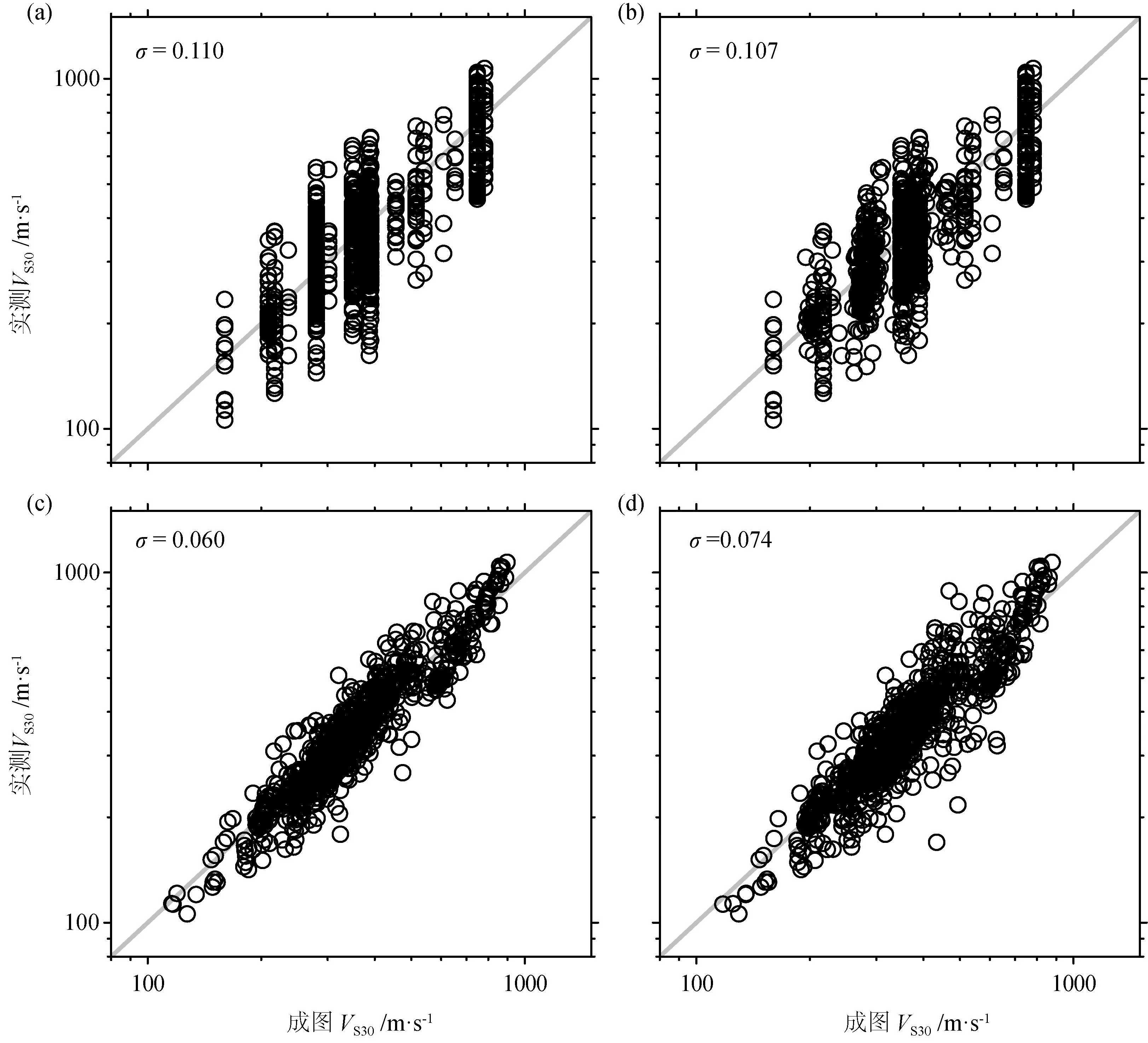
图7　(a)Wills和Clahan(2006)绘制的VS30对实测VS30变化的图；(b)方程(3)～(4)的混合趋势成图的VS30对实测VS30变化的图；(c)全分辨率(3角秒，约90m)回归克里格图成图的VS30对实测VS30变化的图；(d)缩减采样到20角秒(约600m)回归克里格图成图的VS30对实测VS30变化的图。每幅图的左上角给出了以10为底的对数采样标准偏差(s)

另一个评价不确定性的方法是把实测VS30值与各种编图的值进行对比。图7给出了(a)WC06图；(b)混合趋势图；(c)全分辨率(3角秒，约90m)回归克里格图和(d)降低采样到20角秒(约600m)的回归克里格图的预测值对实测值的曲线图。每幅图左上角标出了以10为底的样本标准偏差(s)。这张图表明随地形坡度的趋势虽然解释了一些地质单元内的偏差，但它使s减少不到百分之几。相比之下，回归克里格模型的s明显小得多，为0.06。然而，重要的是要记住，s的值是在具有测量值的位置上算出来的，所以这意味着它有最小的不确定性，不确定性是随距最近的测量值位置的距离而增加的(见图6)。这个值大约相当于图6给出的σE的最低值，而WC06和混合趋势的采样标准偏差接近于图6给出的σE的最大值。图7也说明了缩减采样直到20角秒分辨率增加的不确定性(图7d)，这个分辨率正是典型的地震动区划图计算的分辨率。我们可以看到发散性略有增加，但较粗分辨率的回归克里格图仍比这里考虑的其他图更精确。

不同的读者往往喜欢不同拟合优度的统计数据。因此表2给出了一些本文涉及的每个VS30模型的不同汇总统计数据[只含有地形坡度的模型是Allen和Wald(2009)做的活跃区域30角秒分辨率的改进模型；地质模型是WC06；混合模型是方程(3)～(4)；Hyb-回归克里格模型是指趋势被定义为混合模型的回归克里格模型]。为了完整，并想说明不同汇总统计数据的一些特性，我们也给出了预报数据均值的这些统计数据(视觉上，这将是一幅只有一种颜色的VS30图)。我们还给出了s和以10为底的对数为单位的残差均值(偏离率)、效率系数(E；NashandSutcliffe，1970)与方差缩减[VR=1-(残差的方差)/(数据的方差)]。E和VR的值很相似；像由表2中均值模型的值示出的那样(尽管对任何的常数预测，VR也为0，而不必一定)，当模型完全预测数据时，二者的值为1，预测均值时，二者的值为0。当根据完整数据库来计算这些汇总的统计数据时，合理的解释是虽然对混合模型我们发现了随地形梯度变化的清晰显著的趋势，但这个模型并没有实质的改进(混合模型的s，E和VR实质上不比仅用地质资料的模型的更好)。问题是数据库中多一半的点不受模型地形坡度的影响。因此，我们仅对混合模型地形坡度被应用了的那些点也计算了这些统计数据(Qdf和Qp)。这些值说明通过在地质单元内，考虑地形坡度趋势比仅考虑地质因素的模型要好。

表2　拟合优度汇总，包括样品数(n)、偏离率、标准偏差(s)、效率系数(E)和方差缩减(VR)

Seyhan等(2014)评价了各种VS30成图方法的精度。他们使用Wills和Gutierrez(2008)的方法计算得到s=0.14。虽然Wills和Gutierrez(2008)的方法给出的s值可能比WC06的s值稍微小一些，但为了讨论，我们期望这两种方法的s值相同。Seyhan等(2014)给出的值大于我们在图7中对WC06给出的0.11的值。因为我们计算s时使用了不同的数据库，所以我们的值小一些。我们数据库之所以有较低的数据偏差，肯定是由于在数据来源部分我们所表述的一个事实，即我们去除了一些我们认为是由图WC06错误分类的而形成的离群值。错误分类的问题或许可以由将来更详细的地质图细化来解决。此外，我们分析中的数据筛选步骤，可能夸大了地质模型相对仅用纯地形坡度模型的改进性能，如表2中的汇总统计所示。我们还注意到表2给出的地形坡度模型的偏离率与s和Wald与Allen(2007)对加利福尼亚州给出的几乎是一样的。

5敏感性

弄清楚VS30的变化对地震动的影响程度很重要。在本节，我们对地震动强度对WC06的VS30图和我们所提出的回归克里格图之间差异的敏感性做定量的分析。为此，我们在除了VS30图之外，保持其他所有输入不变的条件下，计算了1994年北岭地震的地震动场景。图8示出了(a)采用WC06VS30图和(b)采用回归克里格VS30图的地震动峰值速度(PGV)图。虽然在地震动峰值速度轮廓线上能够看到一些差异，但通过绘制地震动强度的比值图，这种差异更容易定量化，也看起来更清晰。因此，图8也给出了(c)用WC06VS30图计算与用回归克里格VS30图计算的地震动峰值加速度(PGA)比值图和(d)类似的地震动峰值速度比值图。地震动峰值速度比值距1较大的偏差表明它对VS30的变化比地震动峰值加速度更敏感。在很多区域使用不同VS30图的地震动图上，地震动峰值速度的差异超过了40%。图S2给出了洛马普列塔地震同样的图。我们之所以使用地震动强度的比值而不使用地震动强度之差是因为用地震动强度的比值比用绝对值之差更能表示出相对差别。这类似于检验地震动方程的响应谱残差(例如，Scasserraetal，2009；Atkinson and Boore，2011)时经常做的对数残差分析。

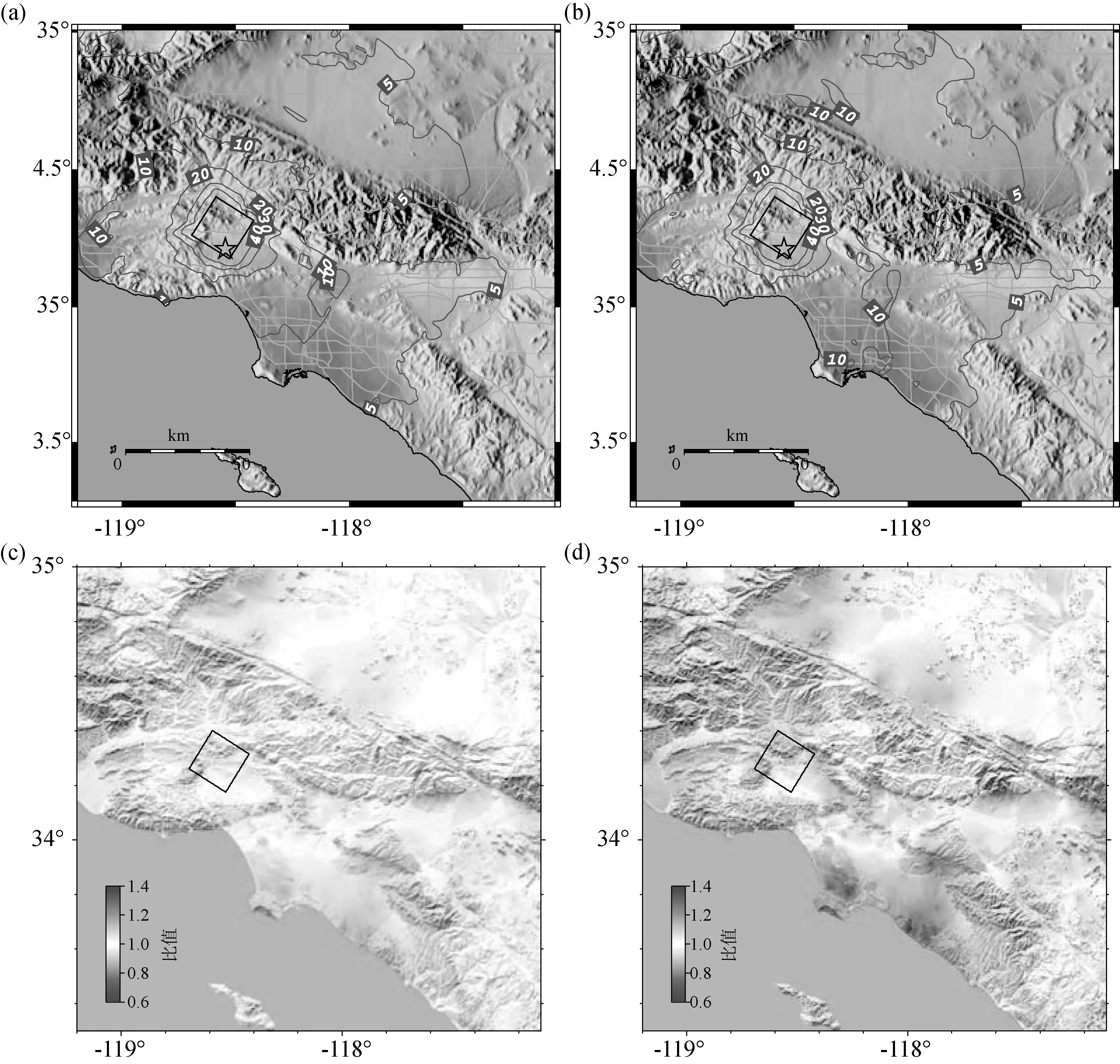
图8　(a)使用Wills和Clahan(2006；WC06)VS30图(原图为彩色图——译注)和(b)使用回归克里格VS30图的1994年北岭地震地震动场景的地震动峰值速度(cm/s)等值线图。星号表识了震中位置，黑框标出了破裂面的地表投影。(c)和(d)也分别示出了使用回归克里格VS30和WC06 VS30图北岭地震的地震动峰值加速度(PGA)比值和地震动峰值速度(PGV)比值

6结论

本文所述的方法利用了最容易得到的辅助(代用物)VS30数据资源：地形坡度、地表地质图和附近的VS30测量数据。因为这种成图方法把这些不同的技术运用于同一张图，可以认为它是一种混合方法。图的精度在空间上变化很大，所以考虑VS30图的同时，也要研究其误差方差(或标准偏差)图对我们来说很重要。我们已经表明，这种方法在测量数据稠密覆盖区域实现了显著改进，这是克里格方法的重要特质；我们在文中所提及的以前的模型不能适应特定场地的VS30值。相对WC06VS30图，我们所提出的VS30图在洛杉矶的很多地方，对1994年北岭地震地震动图的地震动峰值速度调整了超过40%。我们相信，这个更新会对依赖推断VS30值的地震动模拟或分析给予显著改善。

数据与来源

我们使用了太平洋工程分析数据库(Walt Silva，书面通信，2011)和Yong等(2013)的VS30测量数据。按照Wald和Allen(2007)的方法，根据30角秒航天飞机雷达层析成像任务数据库(Farr and Kobrick，2000)计算了地形梯度(即最大地形坡度)，图件是使用通用绘图工具命令“grdgradient”绘制的。Wills和Clahan(2006)的图由Chris Wills提供。

参考文献

Allen，T.I.，and D.J.Wald(2009).On the use of high-resolution topographic data as a proxy for seismic site conditions(VS30)，Bull.Seismol.Soc.Am.99，935-943.

Atkinson，G.M.，and D.M.Boore(2011).Modifications to existing groundmotion prediction equations in light of new data，Bull.Seismol.Soc.Am.101，1121-1135.

Chilès，J.-P.，and P.Delfiner(1999).Geostatistics：ModelingSpatialUncertainty，Wiley，New York，New York，695 pp.

Farr，T.G.，and M.Kobrick(2000).Shuttle Radar Topography Mission produces a wealth of data，EosTrans.AGU81，583-585.

Goovaerts，P.(1997).GeostatisticsforNaturalResourcesEvaluation，Oxford University Press，New York，New York，483 pp.

Magistrale，H.，Y.Rong，W.Silva，and E.M.Thompson(2012).A site response map of the xontinental U.S.，15thWorldConferenceonEarthquakeEngineering，Lisbon，Portugal，24-28 September.

Nash，J.E.，and J.V.Sutcliffe(1970).River flow forecasting through conceptual models：Part I，a discussion of principles，J.Hydrol.10，282-290.

Scasserra，G.，J.P.Stewart，P.Bazzurro，G.Lanzo，and F.Mollaioli(2009).A comparison of NGA ground-motion prediction equations to Italian data，Bull.Seismol.Soc.Am.99，2961-2978.

Seyhan，E.，J.P.Stewart，T.D.Ancheta，R.B.Darragh，and R.W.Graves (2014).The NGA-West 2 site database，Earthq.Spectra，http：//dx.doi.org/10.1193/062913EQS180M.

Thompson，E.M.，and D.J.Wald(2012).Developing VS30 site-condition maps by combining observations with geologic and topographic constraints，15thWorldConferenceonEarthquakeEngineering，Lisbon，Portugal，24-28 September.

Thompson，E.M.，L.G.Baise，R.E.Kayen，E.C.Morgan，and J.Kaklamanos(2011).Multiscale site-response mapping：A case study of Parkfield，California，Bull.Seismol.Soc.Am.101，1081-1100.

Thompson，E.M.，L.G.Baise，R.E.Kayen，Y.Ta-naka，and H.Tanaka(2010).A geostatistical approach to mapping site response spectral amplifications，Eng.Geol.114，330-342.

Wald，D.J.，and T.I.Allen(2007).Topographic slope as a proxy for seismic site conditions and amplification，Bull.Seismol.Soc.Am.97，1379-1395.

Wald，D.J.，L.McWhirter，E.M.Thompson，and A.S.Hering(2011).A new strategy for developingVS30maps，4thIASPEI/IAEEInternationalSymposium：EffectsofSurfaceGeologyonSeismicMotion，Santa Barbara，California，23-26 August 2011.

Wessel，P.，W.H.F.Smith，R.Scharroo，J.F.Luis，and F.Wobbe(2013).Generic Mapping Tools：Improved version released，EosTrans.AGU94，409-410.

Wills，C.J.，，and K.B.Clahan(2006).Developing a map of geologically defined site-condition categories for California，Bull.Seismol.Soc.Am.96，1483-1501.

Wills，C.J.，and C.Gutierrez(2008).Investigation of geographic rules for improving site-conditions mapping，USGSNEHRPFinalTechnicalReport，Award Number 07HQGR0061，20 pp.

Worden，C.B.，D.J.Wald，T.I.Allen，K.Lin，D.Garcia，and G.Cua(2010).A revised ground-motion and intensity interpolation scheme for ShakeMap，Bull.Seismol.Soc.Am.100，3083-3096.

Yong，A.，S.E.Hough，J.Iwahashi，and A.Braverman(2012).A terrainbased site-conditions map of California with implications for the contiguous United States，Bull.Seismol.Soc.Am.102，114-128.

Yong，A.，A.Martin，K.Stokoe，and J.Diehl(2013).ARRA-fundedVS30measurements using multi-technique approach at California and centra-leastern United States strong motion stations，U.S.Geol.Surv.Open-FileRept.2013-1102，59 pp.

杨国栋(1959—)，男，中国科学技术大学硕士研究生毕业，主要从事地震预测研究与实践工作。E-mail：yanggd@gssb.gov.cn。

译 者 简 介

E.M.Thompson，D.J.Wald，C.B.Worden.2014.AVS30map for California with geologic and topographic constraints.Bull.Seismol.Soc.Am.104(5)∶2313-2321.doi∶10.1785/0120130312

杨国栋，高曙德 译.2016.带有地质和地形约束的加利福尼亚州VS30图.世界地震译丛.47(2)∶147-159.doi∶10.16738/j.cnki.issn.1003-3238.201602005

本文的译载由国家自然科学基金(NSFC41174059)资助

甘肃省地震局杨国栋，高曙德译

中国地震局地球物理研究所金严校