基于自适应无迹卡尔曼算法的工业物联网数据融合处理
王春媚
(天津轻工职业技术学院,中国天津300350)
基于自适应无迹卡尔曼算法的工业物联网数据融合处理
王春媚
(天津轻工职业技术学院,中国天津300350)
为提高工业物联网实测数据精度,减少数据冗余、测量误差,提出了一种使用自适应无迹卡尔曼滤波(AUKF)算法对工业物联网中的多传感器信息进行数据融合处理的方法。首先给出并比较卡尔曼算法以及常规无迹卡尔曼(UKF)算法、AUKF算法原理及数学模型;在工业传感器观测值的基础上,分别应用常规UKF、AUKF算法对数据进行融合处理,并对仿真结果进行数值分析。结果表明,使用改进AUKF算法较其他数据融合算法能够显著提高状态估计的准确性和系统稳定性,可适用于工业物联网的实时生产环境。
无迹卡尔曼滤波;数据融合处理;工业物联网
1 引言
随着新型工业化的发展,物联网等信息技术已在工业领域得到了广泛的应用。传统工业模式中简单的数据采集将发展成为具备智能处理能力的信息获取[9]。而工业物联网中普遍存在的传感器节点数量巨大、信息冗余度高、精度低等问题;面对大量异构、混杂的工业物联网数据,数据融合技术的应用成为物联网信息处理的关键[4]。
数据融合技术应用在工业物联网中,可以提高数据精度、采集效率并能减少数据冗余以及传输消耗。因此在数据融合过程中,融合效率和数据精度的提升是数据处理的主要目标,也是评判数据融合算法优劣的关键。针对上述问题,本文使用自适应无迹卡尔曼算法(Adaptive-Unscented Kalman Filtering,AUKF),对工业物联网中多传感器产生的大量冗余数据进行融合处理。
2卡尔曼算法模型
2.1卡尔曼滤波
卡尔曼滤波(Kalman Filtering,KF)是1960年由数学家R.E.Kalman首先提出的著名算法,其成功将状态空间模型应用到卡尔曼滤波器,通过系统的状态方程和输入输出观测数据,利用递推迭代估计算法对系统的状态进行最优估计[1]。这种算法克服了传统维纳滤波(Wiener Filtering,WF)的局限性,成为了当前应用最广的一种动态数据处理算法。
在工业物联网的多传感器系统中,卡尔曼算法可用于对数据的实时融合处理,其最大优点是可以屏蔽随机干扰噪声并减少冗余信息[3],从而降低测量误差且获得更加精准的传感器数据。
2.2卡尔曼滤波算法
卡尔曼算法基本数学模型:
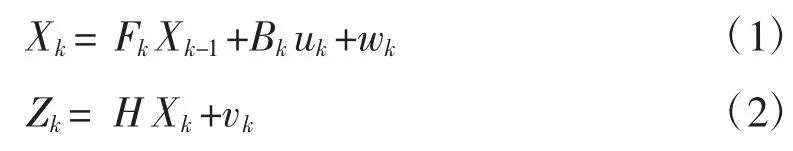
式中,Xk为第k时刻的系统状态值,F为状态转移矩阵,B为输入控制矩阵,wk为过程噪声向量,vk为观测噪声向量,其分布符合wk~N(0,Qk),vk~N(0,Rk),Zk为系统k时刻的观测值,H为状态输出转换矩阵。
根据式(1)、式(2)可以利用系统模型和上个周期的估计值来获得本周期状态的先验估计值(时间更新):

基于当前时刻的观测值和状态的先验估计值,可以得到状态的后验估计值(测量更新):

式中,K表示为卡尔曼系数,Pk为噪声协方差矩阵,I是一个单位矩阵,对于单模型I值为1。式(5)是最佳估计值的校正;式(6)是计算卡尔曼系数K;式(7)为最佳估计值的噪声协方差矩阵的校正;式(3)-式(7)即为卡尔曼滤波的基本方程,其工作流程如图1所示。

图1卡尔曼滤波工作流程图
3自适应无迹卡尔曼模型
经过50多年的发展与应用,初始的卡尔曼滤波算法得到了很大的改进并已发展成一个完整的理论体系。针对工程应用中估值误差均值和误差协方差的不确定性,又出现了衰减记忆滤波、有限下界滤波、平方根滤波、自适应滤波(Adaptive Kalman Filtering,AKF)等卡尔曼算法的改进。
3.1常规UKF算法
无迹(又称无损、去芳香)卡尔曼滤波(Unscented Kalman Filtering,UKF)算法结合无迹变换(Unscented Transform,UT)与卡尔曼线性滤波框架,采用确定性采样策略和多个粒子点逼近函数的概率密度分布,从而获得较传统扩展卡尔曼滤波算法(Extended Kalman Filtering,EKF)更高的精度和稳定性。
UKF的基本原理是根据上一时刻最优值,构造一组Sigma点集{xi},然后对{xi}中每个点进行非线性变换,在保持采样均值和协方差的前提下获得非线性变换之后的状态量和方差。UT变换算法是先得到输入变量的统计量x,利用Sigma点采样策略得到输入变量的Sigma点集wi{xi},以及对应的权值wim与wic。
3.2自适应UKF算法
常规UKF算法克服了EKF算法中的缺点,但在实际工程应用中,由于异常扰动误差与不确定性测量噪声等的影响,UKF算法对时间更新的预测值会出现偏差,导致滤波器性能降低,影响了数据处理精度。因此本文以常规UKF算法为基础,根据自适应估计原理,采用自适应无迹卡尔曼滤波算法(Adaptive-UKF,AUKF)对UKF的预测值进行自适应求取,克服系统不确定因素的影响,提高系统自适应性与滤波估计稳定性。AUKF算法的计算过程如下。
(1)初始化状态参数

在这一步中,初始参数的选取很重要。
(2)状态扩维
由于算法执行过程中需要对噪声等因素进行估计,因此应进行状态扩维。

(3)计算Sigma采样点

(4)时间更新
将Sigma点向后传播:


(5)测量更新
计算输出的预测值及其方差,根据前一步的Sigma点集得到:
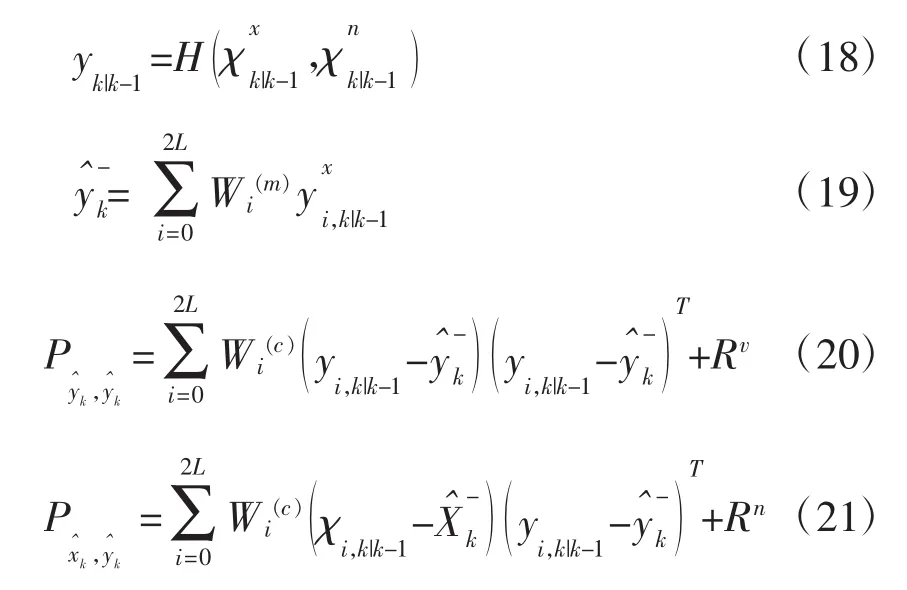
利用实际输出修正计算后验估计值:

式中,Rv表示系统噪声的方差,Rn为观测噪声方差,Wi表示相应权值。
4算法仿真应用
某工厂制造车间布设了10个无线粉尘传感器,用来收集车间PM10浓度信息。对其一小时内采集的所有数据分别利用UKF、AUKF算法进行融合处理。其中传感器数据上传时间间隔均为1min/次,状态参数的初值由前一周的观测结果确定,以工业高精度气体浓度测量仪的数据作为精确测量数值参照。
4.1选取初始参数
将工业物联网中多传感器数据用AUKF数据融合算法进行仿真并将处理结果与原始观测值、常规卡尔曼滤波值相比较。
考虑传感器系统数据为二维数据,而系统观测为一维。观测值采样间隔为ΔT=1min。而整体采样系统,因此滤波器初值为:,

4.2预测阶段
需要先选择计算获得Sigma点采样的方案,本文选取标准化的对称采样法计算Sigma采样点。根据式(15),利用式(26)计算出均值和方差的权值。

式(15)λ=α2(L+k)-L是比例因子,参数α决定Sigma采样点在其均值附近的分布状态,一般选择0≤α≤1,k取值要确保矩阵为半正定矩阵。β的合适选择可以提高方差的精度,考虑应用的系统的状态分布可以认为是高斯分布,这里取α=1e-3,β=2,k=0。其中L是状态的维数,Wi表示相应权值。按照式(16)(17)就可以预测下一时刻的状态和及其方差的预测值。
4.3更新修正阶段
在更新阶段根据上一阶段计算出的预测值,可以得出一组点集(Sigma点集),根据标准UT过程利用式(18)对点集中每一点都进行非线性变换;然后根据式(19)-式(21)计算出预测值y的均值和方差;根据式(23)计算卡尔曼系数。通过式(24)、式(25),利用上一步已计算出的观测值来修正状态量的预测值,就可以算出下一时刻的状态量和方差估计值。最后通过式(21)对系统噪声和噪声方差进行修正。迭代运行就可以进行不断的预测与修正更新。
5结果分析
在本次仿真实验中,将工业物联网采集的十组传感器数据分别用以上常规UKF、AUKF算法通过进行数据融合处理,并与传感器采集的数据(观测值)与高精度工业气体浓度仪的值进行比较。部分数据如表1所示,Matlab仿真结果如图2所示。UKF、AUKF误差分析如图3所示。UKF、AUKF估计值分析如图4所示。

表1多传感器观测值、UKF融合值、AUKF融合值、精确测量值(部分)单位ug/m3

图2算法仿真结果

图3 UKF、AUKF误差分析

图4 UKF、AUKF估计值分析
由于工业现场环境恶劣、干扰较多,由表1可以看出观测值存在较大的误差。图2仿真结果表明,通过UKF、AUKF算法对数据融合分析后的结果相对于测量值有较高的精度,而其中AUKF滤波融合后的结果与精确值更为接近,因此AUKF算法在本实验中达到了很好的滤波估计效果,可以有效地提高工业物联网中多传感器数据监测的精度。
通过对实验数据融合结果进行误差分析,如图3所示。可以看出,UKF算法融合的误差比AUKF的大,证明了AUKF算法较UKF算法降低了系统误差。根据图3可以看出,仅约30次卡尔曼迭代后AUKF算法的估计值就已经非常逼近真实值,而UKF还存在很大的偏差。通过调整相应数学模型系数可以使算法获得更好的性能,但修改不当会使得卡尔曼系数发生较大的改变,会降低算法对数据融合处理的准确度。甚至使得卡尔曼滤波器发散。
6结论
在工业物联网传感器的数据处理中,为提高多传感器数据精度,解决数据冗余和稳定性问题,本文提出了一种根据工业环境改进的自适应无迹卡尔曼(AUKF)算法,并利用典型的工业传感器数据进行仿真,得出了以下结论。
传统滤波算法需要确定的系统模型和先验信息,实际中因无法获得这些确定的信息会导致滤波器性能低下。基于UKF算法改进的AUKF算法仅需要传感器的观测数据就可以得出待估计状态的最优估计,能更加灵活地满足工业现场数据实时性要求。
AUKF算法继承了常规UKF算法的强项,且在滤波融合过程中,其实时自适应调整能力进一步提高了数据融合精度,因此AUKF算法可以很好地实现多传感器融合,降低测量误差,减少数据冗余,提高数据精度,非常适合用于工业底层冗余传感器的数据融合处理。
UKF算法会因为系统异常扰动而影响整体滤波性能,AUKF算法因为其良好的自调节能力能够在一定程度上克服异常扰动误差对系统的影响,使得整体稳定性更高,满足工业应用中复杂的生产环境。
[1]蔡鹤皋,金明河,金 峰.卡尔曼滤波与多传感器数据融合技术[J].模式识别与人工智能,2000,13(3):248-253.
[2]李洪亮,时 荣,钟 双.自适应卡尔曼滤波在大坝形变预报中的应用分析[J].测绘技术装备,2015,17(1): 48-52.
[3]赵洪山,田 甜.基于自适应无迹卡尔曼滤波的电力系统动态状态估计[J].电网技术,2014(1):188-192.
[4]Sasiadek J.Fuzzy adaptive Kalman filtering for INS/GPS data fusion[J].Proc.ieee Int.symp.intell.control,2000: 181-186.
[5]李 峰.在农业物联网中基于卡尔曼滤波算法实现系统数据的融合处理[J].农业网络信息,2014(12):13-15.
[6]卢胜利,刘美玲,田彦彦.基于卡尔曼滤波的多温度传感器数据融合系统[J].现代科学仪器,2013(1):65-68.
[7]吴 萌,马 杰,田金文等.自适应无迹卡尔曼滤波算法在地磁导航中的应用[J].信息与控制,2011,40(4): 558-562.
[8]赖 韬,伊廷华,王健宇等.基于多速率卡尔曼滤波方法的位移和加速度数据融合[J].防灾减灾工程学报,2012(6).
[9]王 浩,李 玉,秘明睿等.一种基于监督机制的工业物联网安全数据融合方法[J].仪器仪表学报,2013,34(4):817-824.
[10]Sun S L,Deng Z L.Multi-sensor optimal information fusion Kalman filter☆[J].Automatica,2004,40(6): 1017-1023.
[11]Yang Y,Gao W.An Optimal Adaptive Kalman Filter[J].Journal of Geodesy,2006,80(4):177-183.
[12]李 鹏,宋申民,陈兴林.自适应平方根无迹卡尔曼滤波算法[J].控制理论与应用,2010,27(2):143-146.
Data fusion processing of the Internet of industrial things based on adaptive unscented Calman algorithm
WANG Chun-mei
(Tianjin Vocational Technical College of Light Industry,Tianjin 300350,China)
As regard to the Internet of industrial things and in order to improve the measured data accuracy,reduce the data redundancy and the measurement error,the method of data fusion processing for the multi-sensor information of the Internet of industrial things based on adaptive unscented Kalman filter(AUKF)algorithm is presented.The principles and the mathematical models of the Kalman algorithm and the conventional UKF and AUKF algorithms are given and compared.Based on the observed values of the industrial sensors,the data are processed by respectively using the conventional UKF and AUKF,and the simulative results are numerically analyzed.The simulation results show that the improved AUKF algorithm can greatly improve the accuracy of state estimation and system stability,and it can be used in the real time production environment of the industrial things.
unscented Kalman filter;data fusion processing;Internet of industrial things
TM351
A
2016-06-15
1005—7277(2016)04—0043—05
王春媚(1980-),汉族,天津市南开区人,硕士,副教授,就职于天津轻工职业技术学院,研究方向为电子通信。

