高超声速飞行器纵向内环系统反演预设性能控制

李海燕，许江宁，张金鹏，张公平，郑鲲鹏

(1. 海军航空工程学院 控制工程系，山东 烟台　264001； 2. 海军工程大学 导航工程系，武汉　430033；3. 中国空空导弹研究院，河南 洛阳　471009)



高超声速飞行器纵向内环系统反演预设性能控制

李海燕1,2，许江宁2，张金鹏3，张公平3，郑鲲鹏3

(1. 海军航空工程学院 控制工程系，山东 烟台264001； 2. 海军工程大学 导航工程系，武汉430033；3. 中国空空导弹研究院，河南 洛阳471009)

摘要:针对高超声速飞行器控制器设计没有考虑系统的瞬态和稳态性能应满足预设性能的 问题，在模型中存在强非线性的条件下，基于反演设计思想，提出一种预设性能控制器的设计方 法。利用Lyapunov 稳定性定理证明了系统的稳定性，保证纵向内环闭环系统误差全状态满足预设 的瞬态和稳态性能。通过仿真算例验证了提出方法的有效性。

关键词:高超声速飞行器; 反演; 预设性能

0引言

由于飞行速度和特殊的飞行环境，高超声速飞行器具有比传统飞行器更为复杂的强耦合、 强非线性和强时变的动力学特性，其控制技术也面临着传统飞行器控制所未曾遇到的新型复杂问题[1-4]。 从20世纪90年代开始，学者们首先研究了线性控制方法，在此基础上研究了非线性控制方法，最后向多方法结合的方向发展。

在鲁棒控制框架内，Gregory利用最优轨迹，通过D-K迭代的方法设计了H∞鲁棒控制器[5]； Heller等人提出基于输出反馈的鲁棒控制器，实现了速度和高度控制[6]； Sigthorsson等提出一种新的内模控制方法进行了输出控制器的设计，实现高超声速飞行器高度和速度的鲁棒跟踪[7]。

线性控制方法难以满足控制需求，学者们研究了非线性动态逆、 反馈线性化的控制方法和其他非线性控制方法。

Gunnarsson等[8]提出了基于动态逆和μ分析结合的方法； Wang和Stengel则采用了非线性动态逆和随机鲁棒结合的方法[9]； Parker等人提出基于鲁棒二次调节器和近似反馈线性化结合的控制方法[10]； 文献[11]则提出一种反馈线性化与多输入多输出自适应滑模控制结合的方法； 文献[12]提出一种基于非线性干扰观测器的滑模反演控制方法； Cox等人提出一种自适应神经网络飞行控制器的设计方法，适应飞行器参数时变、 扰动等特性的变化[13]。

上述方法都没有考虑系统的控制性能问题，无法保证闭环系统的瞬态性能。 预设性能控制问题可追溯到Miller和Davison的开创性的工作[14]； 文献[15-18]进一步讨论了非线性系统的预设性能控制器设计问题； Ilchmann等人提出了一种增益无需动态产生和非单调增益的预设性能控制方法[16]； Bechlioulis等人提出一种鲁棒自适应控制器设计方法，实现系统的最大超调量小于事先设定的足够小的常数[17]。

本文针对上述高超声速飞行器控制系统设计没有考虑同时满足瞬态性能和稳态性能的要求、 反演设计中预设性能控制器的设计仅能实现输出变量达到预设性能等问题，提出一种新的预设性能控制方法，之所以研究纵向系统的控制问题是因为该子系统是最具高超声速飞行器典型特征和最具控制挑战性的[19]。

1系统描述及预备知识

1.1吸气式高超声速飞行器纵向系统描述

吸气式高超声速飞行器纵向动力学模型可表示为[20]

(1)

式中:V为飞行速度；T为推力；α为迎角；D为阻力；m为飞行器的质量；g为重力加速度；L为升力；M为俯仰力矩；Iyy为转动惯量；θ为俯仰角；q为俯仰角速度。

力、 力矩以及相关的系数可以用式(2)～(3)表示:

(3)

进一步推导之前，先做如下假设： 假设1: 在升力L中忽略升降舵偏角δe对其的影响； 假设2： 高超声速飞行器的飞行速度V变化较慢，与迎角α、 俯仰角速度q相比属于慢变量。

吸气式高超声速飞行器可分为内环和外环两个子系统，内环控制的控制量为升降舵偏角δe，控制迎角α和俯仰角速度q跟踪期望值，外环控制利用内环子系统的输出α，q和当量比φ控制飞行速度，从而实现整个纵向系统的控制。 在此仅研究内环子系统的设计问题。 利用假设1和2，吸气式高超声速飞行器的内环快变子系统可以表示为

(4)

式中：

1.2预设性能与误差变换函数[18]

假设e(t)为跟踪误差，预设性能ϖ(t):R+→R+-{0}是一个正的递减函数，对所有t≥0满足

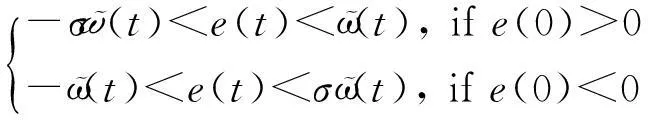
(5)

e(t)=ϖ(t)Φ(S)

(6)

式中：S为变换后误差；Φ(S)为平滑、 严增且可逆的函数，满足如下性质：

(7)

(8)

从式(8)知，如果S有界，则式(7)成立。 另外，由ϖ(t)>0和式(6)可知，当e(0)>0时，-σϖ(t)<ϖ(t)Φ(S)=e(t)<ϖ(t)； 当e(0)<0时, -ϖ(t)<ϖ(t)Φ(S)=e(t)<σϖ(t)，故式(5)成立。 因此，只要S∈L∞，就可以实现预设性能。

对任意常数η>0 和变量p∈R，下式成立[21]：

(9)

[1-2tanh2(S/ε)]<0

(10)

2预设性能控制器设计

预设性能控制器的设计步骤如下：

(11)

(12)

令e2=q-qd，qd为待设计的虚拟控制量。 将e2的表达式代入式(12)可得

(13)

定义Lyapunov函数

(14)

求取方程(14)随时间的导数得到

(15)

选择虚拟控制律

(16)

式中: k1>0为常数。 将式(16)代入式(15)可得

(17)

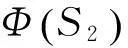
(18)

(19)

选择Lyapunov函数为

(20)

求取方程(20)随时间的导数得到

(21)

令

(22)

式中：ε2>0，k2>0，均为常数。

根据式(9)，式(22)所示控制规律可以实现。 由于双曲函数的引入，所设计的控制器有一定的鲁棒性。

将式(22)代入式(21)得

(23)

(24)

故S1和S2均有界。

由上述分析知，由于S1和S2均有界，故e1和e2均实现了预设性能跟踪。 可以得出：对于内环子系统式(4)，如果虚拟控制律按照式(16)选取，控制律按照式(22)选取，则系统所有信号均有界且实现预设跟踪性能。

3仿真验证

为验证本文所提出预设性能控制方法的有效性，进行了迎角指令跟踪的仿真研究。 针对内环子系统式(4)，气动力、 力矩系数名义值采用文献[20]提供的数据，控制器采用本文设计的预设性能控制器，控制的目标是使飞行器以给定的预设性能跟踪期望的迎角指令。

仿真的初始条件设定如下：V=2 800m/s; φ=0.6; α(0)=3.5°; q(0)=0.6°; αd=4°。 系统的参数参见文献[20]。

仿真结果如图1～4所示。 图1为迎角α跟踪期望信号αd的响应曲线； 图2为俯仰角速度q跟踪期望俯仰角速度qd的曲线； 图3为e1及相应预设性能曲线； 图4为e2及相应预设性能曲线。 可以

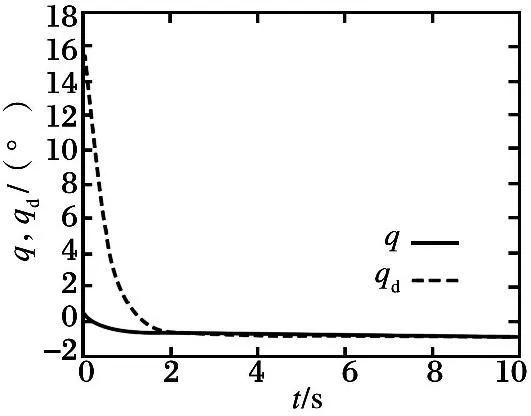
图1　迎角跟踪曲线

图2　俯仰角速度跟踪曲线

图3　e1及相应预设性能曲线

图4e2及相应预设性能曲线

看出，迎角很好地跟踪上了期望迎角信号，俯仰角速度也较好地跟踪上了期望俯仰角速度信号，且e1和e2均实现了预设性能，验证了所设计控制器的有效性。

4结论

针对高超声速飞行器纵向运动学的内环子系统模型具有高度非线性、 耦合性等特点，提出一种基于预设性能的控制器设计方法，实现全状态具有预设性能，解决了现有大多数高超声速飞行器控制器设计研究中未能考虑稳态和瞬态同时具有预设性能的问题。 仿真结果表明，所提出的控制方法具有较好的跟踪性能。 需要指出的是本文仅对高超声速飞行器纵向运动学的内环子系统进行了预设性能控制研究，而且没有考虑不确定性，这也是下一步需要深入研究的问题。

参考文献：

[1] 孙长银, 穆朝絮, 余瑶. 近空间高超声速飞行器控制的几个科学问题研究[J]. 自动化学报, 2013, 39(11): 1901-1913.

[2] 王鹏飞, 王洁, 时建明, 等. 吸气式高超声速飞行器控制研究综述[J]. 航空兵器, 2015(3)： 3-7.

[3] 张靖男, 孙未蒙, 郑志强. 高超声速武器控制技术发展探讨[J]. 航空兵器，2006(4)： 11-13.

[4] 邵雷, 雷虎民, 赵宗宝, 等. 临近空间高超声速飞行器建模与控制研究进展[J]. 航空兵器, 2013(4)： 20-24.

[5] Gregory I M, Chowdhry R S, McMinn J D, et al. Hypersonic Vehicle Model and Control Law Development Using H∞and μ Synthesis[R]. NASA Technical Memorandum, 1994.

[6] Heller M, Sachs G, Gunnarsson K S, et al. Flight Dynamics and Robust Control of a Hypersonic Test Vehicle with Ramjet Propulsion[C]∥Proceedings of the 8th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Reston, Virginia, 1998.

[7] Sigthorsson D O, Jankovsy P, Serrani A, et al. Robust Linear Output Feedback Control of an Airbreathing Hypersonic Vehicle[J].Journal of Guidance, Control, and Dynamics, 2008, 31(4): 1052-1066.

[8] Gunnarsson K S, Jacobsen J O. Design and Simulation of a Parameter Varying Controller for a Fighter Aircraft[C]∥Proceedings of the 2001 AIAA Guidance, Navigation, and Control Conference and Exhibit, Montreal, Canada, 2001.

[9] Wang Qian, Stengel R F. Robust Nonlinear Control of a Hypersonic Aircraft[J].Journal of Guidance, Control, and Dynamic, 2000, 23(4): 577-585.

[10] Parker J T, Serrani A, Yurkovich S, et al. Approximate Feedback Linearization of an Air-Breathing Hypersonic Vehicle[C]∥AIAA Guidance, Navigation, and Control Conference and Exhibt, Keystone, Colorado, 2006.

[11] Xu Haojian, Mirmirani M, Ioannou P A. Adaptive Sliding Mode Control Design for a Hypersonic Flight Vehicle[J].Journal of Guidance, Control, and Dynamics, 2004, 27(5): 829-838.

[12] 卜祥伟, 吴晓燕, 陈永兴, 等.基于非线性干扰观测器的高超声速飞行器滑模反演控制[J].控制理论与应用, 2014，31(11)： 1473-1479.

[13] Holm-Hansen B, Lee H P, Youssef H M.Neuro-Fuzzy Dynamic Inversion Control for a Hypersonic Cruise Vehicle[C]∥AIAA Guidance, Navigation, and Control Conference, Toronto, Ontarlo Canada，2010.

[14] Miller D E, Davison E J.An Adaptive Controller Which Provides an Arbitrarily Good Transient and Steady-State Response[J].IEEE Transactions on Automatic Control, 1991, 36(1): 68-81.

[15] Kostarigka A K, Rovithakis G A.Adaptive Dynamic Output Feedback Neural Network Control of Uncertain MIMO Nonlinear Systems with Prescribed Performance[J].IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(1): 138-149.

[16] Ilchmann A, Logemann H, Ryan E P.Tracking with Prescribed Transient Performance for Hysteretic Systems[J].Siam Journal on Control and Optimization, 2010, 48(7): 4731-4752.

[17] Bechlioulis C P, Rovithakis G A. Robust Adaptive Control of Feedback Linearizable MIMO Nonlinear Systems with Prescribed Performance[J].IEEE Transactions on Automatic Control, 2008, 53(9): 2090-2099.

[18] 张秀宇，林岩.具有磁滞输入非线性系统的鲁棒自适应控制[J]. 自动化学报，2010，36(9)： 1264-1271.

[19] Bolender M A, Doman D B. Nonlinear Longitudinal Dynamical Model of an Air-Breathing Hypersonic Vehicle[J].Journal of Spacecraft and Rockets, 2007, 44(2): 374-387.

[20] Parker J T, Serrani A, Yurkovich S, et al. Control-Oriented Modeling of an Air-Breathing Hypersonic Vehicle[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 856-869.

[21] Levant A. Higher-Order Sliding Modes, Differentiation and Output-Feedback Control[J].International Journal of Control, 2003, 76(9-10): 924-941.

Backstepping Control with Prescribed Performance for Longitudinal Inner-Loop System of Hypersonic Vehicles

Li Haiyan1,2, Xu Jiangning2, Zhang Jinpeng3, Zhang Gongping3, Zheng Kunpeng3

(1. Department of Control Engineering, Naval Aeronautical and Astronautical University，Yantai 264001，China;2. Department of Navigation Engineering, Naval University of Engineering, Wuhan 430033, China;3. China Airborne Missile Academy，Luoyang 471009，China)

Abstract:For the controller design of hypersonic vehicles, the problem that transient and steady state performance of system should satisfy the prescribed performance is not considered. Based on backstepping design idea, a controller design method with prescribed performance is proposed under the strong nonlinearity existing in the design model. It is proved that the system is stable by Lyapunov stability steorem and all error states of the longitudinal inner closed-loop system of hypersonic vehicles satisfy the prescribed transient and steady state performance. The simulation results demonstrate the effectiveness of the proposed method.

Key words:hypersonic vehicle; backstepping; prescribed performance

中图分类号:V249． 1

文献标识码:A

文章编号:1673-5048( 2016) 02-0024-05

作者简介：李海燕(1979-)，女，吉林长春人，副教授，博士，研究方向为非线性控制。

基金项目：航空科学基金项目(20140184001)； 中国博士后科学基金项目(2015M572693)

收稿日期：2015-09-13

DOI：10.19297/j.cnki.41-1228/tj.2016.02.004