单层网壳静力稳定性研究

黄卫林（广州大学土木工程学院）



单层网壳静力稳定性研究

黄卫林
（广州大学土木工程学院）

【摘要】以K6型单层球面网壳为研究对象，基于非线性有限元理论，研究考虑结构初始几何缺陷、材料非线性以及几何非线性对该网壳结构静力整体稳定性的影响，论述了两类稳定性问题，线性屈曲分析计算得到临界荷载以及屈曲模态，非线性屈曲分析方法为弧长法，分析得到网壳结构的荷载-位移全过程曲线，具有工程实际意义。

【关键词】单层网壳；静力稳定性；屈曲分析；初始缺陷

1　引言

网壳结构不仅具有重量轻、刚度大、受力合理、造价低廉等优点，而且其具有丰富的结构型式，造型十分美观，其概念一经提出备受国内外关注，展现了广阔发展前景广泛应用于中小型建筑、建筑厂房以及较大跨度的博览馆、航空港等公共建筑［1］。单层网壳结构属于缺陷敏感性结构，设计时提出了安全系数和临界荷载。网壳结构承载力的设计往往是由稳定性决定。而单层网壳结构的稳定性分析十分繁琐，失稳模态可分为整体失稳、局部失稳和单杆件失稳。影响结构失稳的因素［2］有很多，如结构的支承条件、初始缺陷的引入、网格划分形式、荷载的不对称分布以及矢跨比等等。

由于初始缺陷对单层网壳结构的影响十分敏感，甚至由于非常小的几何缺陷存在导致其临界荷载明显降低，任何结构都存在初始缺陷，这是不可避免的，这样计算得到的临界荷载与理想情况分析的结果有一定差距。而目前研究初始缺陷问题还没有统一的、准确的研究方法。目前考虑初始缺陷来求解几何非线性刚度矩阵［3］的方法有：能量平衡技术、弧长法以及NR法、增量法、最小残余位移法等。其中最有效、最实用的方法为弧长法，该方法能分析屈服问题全过程，可研究结构的下降段曲线。

2　单层网壳结构静力稳定性分析

2.1静力分析方法

采用空间梁单元Beam188［4］元来模拟单层网壳的杆件，基于有限元理论的离散化分析方法，求解分析较为精确。结构计算分析的总刚度方程为：

［K］［D］=［W］

式中，K为刚度矩阵；D为位移向量；W为荷载向量。结构的总体刚度矩阵K反映了结构在某一平衡状态的稳定性［5］。判别其达到临界状态的标志就是刚度矩阵，从计算的结果可区分临界点为极值点或者是分歧点。当临界状态表现为极值点屈曲时，屈曲后的研究方法与前屈曲相同，当临界状态表现为分歧点屈曲时，求解时引入初始缺陷转换为极值平衡的路径。具体过程分别如图1、图2。

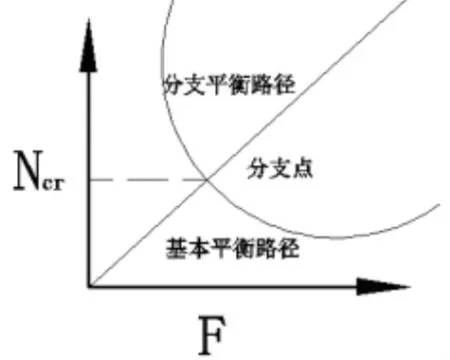
图1　特征屈曲失稳示意图

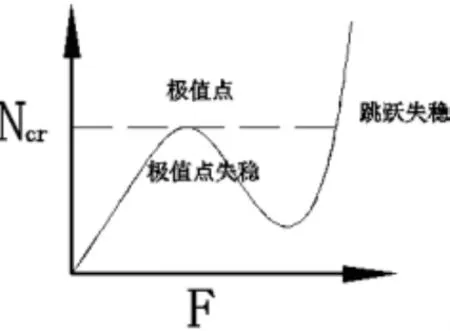
图2　非线性失稳示意图

传统单层网壳结构的整体稳定性分析比较成熟，而考虑初始缺陷、双重非线性分析、和荷载不利布置的影响等研究相对较少，目前该结构理论基础和工程应用十分广泛［6］。合理网壳结构受力性能的关键是曲面形状。

2.2单层网壳结构两类稳定性问题

当结构在极限荷载作用下，若再稍微增大一点荷载，此时结构将发生巨大的的平衡位移，这就称为结构失稳或者结构屈曲。特征值屈曲分析是分析结构整体稳定性的基本方法，其概念清晰、计算简单，计算得到的屈曲模态视为初始几何缺陷施加在结构中进行非线性稳定研究［7］。单层网壳结构最大的特点就是稳定性是其设计的最为关键的问题。根据结构失稳的性质，有限元ansys的屈曲分析方法有两类∶特征值屈曲分析和非线性屈曲分析。

目前有关单层网壳结构稳定性理论的研究有：杨笑天［8］等对采用数值逆吊法来找形分析，研究了单层网壳结构杆件内力的变化、结构的变形和动力的稳定性。沈晓明［9］等基于ansys有限元软件单层网壳进行了特征值屈曲分析，考虑初始缺陷在满跨和半跨荷载作用下分析了其失稳的一般规律。曹正罡［10］等深入研究了单层球面网壳的弹塑性稳定性能。范峰［11］等探讨了单层网壳结构考虑几何非线性、材料非线性以及弹塑性非线性的极限承载力。郭海山［12］等提出了动力响应全过程曲线的理论，采用时程响应曲线详细研究了网壳结构的动力稳定性特征。聂义田［13］等推导了单层球面网壳结构稳定性简便计算公式，较为精确地计算网桥结构的极限承载力，详细论述了单层网壳稳定性影响因素∶结构的拓扑形式、初始缺陷、非线性网壳曲率大小、荷载均匀分布等基本参数。沈金［14］等分析了4个K8型不同矢跨比的单层网壳结构进行荷载-位移分析，给出了网壳稳定性模态的建议取值。

3　计算模型

工程实际中常用的单层球面网壳结构有kiewitt、肋环型、联方形及短程线型等多种网壳球面形式，它们的稳定性能既有球面网壳的相似性，又有自身的特点。在实际工程中，常用的网壳型式为Kiewitt型，主要的原因是该种网壳结构的网格划分较均匀且操作简便，整个结构的杆件类型较少，工程施工速度快、工艺简单。本文主要研究K6型单层球面网壳的静力分析、两类稳定性和考虑初始缺陷的极限承载力等问题。网壳球面结构杆件选用热轧无缝钢管，单层网壳支撑体系选用梁单元模拟，两端采用刚接；衔架中腹杆根据其受力特性选用杆单元，两端为铰接，柱脚采用铰接。该网壳模型的计算跨度为50m，共布置5圈杆件，矢高为10m，模型如下图1所示，网壳杆件采用φ152mm×8mm的钢管，查表得截面惯性矩为I=940.97cm2，截面面积A=0.003619m2，其截面的回转半径i=0.051m，弹性模量取E=2.1×105MPa，考虑材料非线性，钢管的屈服极限值为310MPa。有限元模拟得到模型平面、立面图分别为图3、图4所示。

3.1静力分析

3.1.1荷载

⑴屋盖恒载：结构自重、装饰部分的材料附加重量、屋盖悬挂荷载、建筑面层，屋面排水沟等。重力荷载在有限元模型中设定材料密度来考虑。恒荷载取800N/m2。

⑵风荷载：单层网壳结构的基本风压风荷载为500N/m2。⑶活载：该结构为不上人的屋面活荷载取500N/m2。⑷雪荷载：参考《建筑结构荷载规范》基本雪压为350N/m2。

3.1.2静力分析结果

考虑恒载、活荷载、风荷载及雪荷载下多种工况组合分析，限于篇幅，取最不利荷载组合为1.2倍恒荷载+1.4倍活荷载+0.84倍风荷载。分析得到结构中点的位移最大为dmx=7.8mm，比规范规定的50000/400=125mm限值小得多。结构的变形图、结构的位移云图分别如图5、6所示。

图3　平面图

图4　立面图

图5　结构变形图

图6　结构位移云图

3.2稳定分析

3.2.1特征值屈曲分析

特征值屈曲分析［15］是理想化的研究：当结构承受荷载值达到极限时，其平衡状态发生明显的、质的变化，即平衡分岔失稳状态或分支点失稳状态。该特征值基于采用弹性屈曲分析方法采用数学方法可求解。但特征值屈曲分析过于保守，实际的工程分析不适用。主要原因在于：初始缺陷、材料、结构非线性的存在使得结构发生弹塑性屈曲，通过有限元ansys软件分析得到特征值屈曲值（见表1），分析得到网壳线性屈曲的第一、第二阶特征值如图7、图8所示。

表1　特征值屈曲值

图7　1阶屈曲模态

图8　2阶屈曲模态

3.2.2非线性屈曲分析

目前考虑初始几何缺陷［16］的结构整体稳定性分析方法有两种［17］：一致缺陷模态法和随机缺陷模态法。准确确定初始几何缺陷大小、分布模式是十分困难的。《空间网格结构技术规程》（JGJ7-2010）［18］给出了最大初始缺陷的合理取值为1/300：可将一阶屈曲模态位移值得0.1倍作为初始几何缺陷分布修改模型的节点坐标，从而进行网壳全过程分析，该方法概念清晰、应用简单、工作量小、可操作性强。随机缺陷模态法最大的优势就在于体现了结构真实的工作性能，不足的是得反复计算不同缺陷的分布概率，计算相当复杂繁琐。

非线性屈曲分析是大变形情况下的结构失稳。结构失稳的临界载荷从荷载-变形全过程曲线的荷载极值点分析得到，该方法逐渐增加载荷的非线性静力分析技术来求得失稳的临界载荷，较为精确，实际工程中应用广泛。现阶段常用弧长法［19］进行非线性屈曲分析。网壳结构的全过程曲线相对复杂，考虑到实际工程的应用，仅取保留曲线超过第一个临界荷载点以及后面必要的一段屈曲路径进行分析，而之后的曲线由于结构位移增加过快，没有很大的实际意义。确定了结构的极限荷载为首个临界点处的荷载值相，可分析得到此结构对应的屈曲模态。弧长法利用ansys有限元APDL语言编制命令流，设定荷载子步数为100，基于位移收敛准则，在结构支座位移最大时终止求解，输出所有的结果文件，得到荷载位移-曲线。节点20最大位移设为1m，考虑初始缺陷为网壳结构跨度的1/300，从节点20的荷载位移曲线如图9。

图9　K6单层网壳荷载-位移曲线

荷载-位移全过程曲线［20］能准确地分析结构的稳定性、刚度、强度以及整个内力变化的过程。传统的线性分析则将结构的强度和稳定性分开独立研究，而考虑结构非线性的分析论证了网壳结构稳定性与强度相互影响的关系，结构的荷载-位移全过程曲线对于考虑几何缺陷的非线性分析是十分有效的。

4　结论

⑴通过对K6型单层球面网壳结构的静力稳定性分析，基于网壳结构的静力分析理论，研究了计算跨度为50m、矢高10m、布置5圈的结构位移。总结了网壳结构两类稳定分析的方法和应用：第一类稳定分析得到的计算结果只提供设计临界荷载上限的参考；而第二类稳定分析充分考虑材料及几何双重非线性等因素的影响，使结构的稳定安全系数明显降低，所以第二类失稳问题具实际参考价值。

⑵研究了影响单层网壳稳定性的影响因素∶结构的拓扑形式、初始缺陷、节点构造、非线性网壳曲率大小、荷载均匀分布等基本参数对结构稳定性的影响。稳定承载力系数随初始几何缺陷的增大而减小，当增大到一定程度时，其影响效果会减小。

⑶对于单层网壳结构，考虑初始几何缺陷整体稳定性分析方法大致分为两种：一致缺陷模态法和随机缺陷模态法。非线性屈曲分析得到的荷载-位移全过程曲线能准确地分析结构的稳定性、刚度、强度以及整个变化的过程。●

【参考文献】

［1］曹正罡，范峰，沈世钊.大矢跨比单层球面网壳弹塑性稳定性研究［J］.哈尔滨工业大学学报，2008，02∶183-186.

［2］桂国庆，王玉娥.短程线型单层球面网壳结构在地震作用下的动力稳定性［J］.工业建筑，2009，07∶103-106.

［3］唐敢，王法武，吴靖坤.具有随机几何缺陷的大跨度单层球面网壳稳定性分析［J］.钢结构，2008，05∶1-6.

［4］殷志祥，李会军.大跨度拉索预应力带肋单层球面网壳的稳定性及应用研究［J］.工程力学，2008，08∶48-52+63.

［5］曹正罡，范峰，沈世钊.K6型单层球面网壳的弹塑性稳定［J］.空间结构，2005，03∶22-26

［6］李永梅，张毅刚.新型索承网壳结构静力、稳定性分析［J］.空间结构，2003，01∶25-30.

［7］董石麟，郑晓清.节点刚、铰接时环向折线形单层球面网壳静力和稳定性能的分析研究［J］.建筑钢结构进展，2013，06∶ 1-11+41.

［8］杨笑天，周健，苏骏.不规则边界单层网壳找形分析与结构设计［A］.天津大学、天津市钢结构学会.第十五届全国现代结构工程学术研讨会论文集［C］.天津大学、天津市钢结构学会，2015.6.

［9］沈晓明，舒赣平.不规则划分单层网壳结构稳定性分析［J］.建筑结构，2009，S1∶101-104.

［10］曹正罡，范峰，沈世钊.单层球面网壳的弹塑性稳定性［J］.土木工程学报，2006，10∶6-10.

［11］范峰，严佳川，曹正罡.考虑杆件初弯曲的单层球面网壳稳定性能［J］.东南大学学报（自然科学版），2009，S2∶158-164.

［12］郭海山，钱宏亮，沈世钊.地震作用下单层球面网壳结构的动力稳定性［J］.地震工程与工程振动，2003，01∶31-37.

［13］聂义田，李亚敏，王丽.单层球面网壳结构稳定性的双重非线性分析［J］.结构工程师，2013，04∶57-62.

［14］沈金，杨军，马洪步.单层K8型椭球面网壳的静力稳定性分析［J］.空间结构，2009，01∶69-72.

［15］韩庆华，杨志，潘延东，刘锡良.单双层球面网壳结构的静力特性及其稳定性能分析［J］.天津大学学报，2002，04∶447-451.

［16］李元齐.某工程单层球面网壳结构的稳定性研究［J］.工业建筑，2001，02∶46-47+1

［17］曹正罡，陈肖达，范峰.均布荷载作用下单层球面网壳的弹塑性失稳模式研究［J］.建筑钢结构进展，2011，06∶19-23+30.

［18］刘宗发，李正良，晏致涛.单层球面网壳的优化分析［J］.重庆建筑大学学报，2005，27（1）∶67-70.

［19］JGJ 7-2010.空间网格结构技术规程［S］.

［20］张帅，韩庆华.某单层球面网壳结构整体稳定性分析［J］.低温建筑技术，2012，03∶40-42.

［21］张春丽，李正良，赵一，邵福建.荷载非对称分布对单层球面网壳稳定性的影响［J］.重庆建筑大学学报，2004，02∶63-67.