隧道窑冷却带流-固耦合散热数值模拟

许宁，王雪峰，张柱银，王 君，黄建军，肖 慧，郅 晓（. 盐城工学院机械工程学院，江苏 盐城 05；. 湖南工业大学机械工程学院，湖南 株洲 007；. 中国建材西安墙体材料研究设计院，陕西 西安 7006；. 中国建筑材料集团有限公司，北京 0006）



隧道窑冷却带流-固耦合散热数值模拟

许宁1， 2，王雪峰1，2，张柱银2，王 君2，黄建军1，肖 慧3，郅 晓4
（1. 盐城工学院机械工程学院，江苏 盐城 224051；2. 湖南工业大学机械工程学院，湖南 株洲 412007；3. 中国建材西安墙体材料研究设计院，陕西 西安 710061；4. 中国建筑材料集团有限公司，北京 100036）

摘 要：以某烧结砖隧道窑为研究对象，为获得隧道窑冷却带散热温度场数据，建立了隧道窑窑壁-砖块-流体耦合传热物理模型与数学模型，采用FLUENT流体计算软件对其进行了隧道窑窑壁-砖块-流体耦合传热仿真，获得了窑内整体比较精确直观的温度场分布。仿真的结果表明：风速为5 m/s、孔隙率为0.5以及砖块适当稀码时，隧道窑冷却带降温效果较好，其与隧道窑烧成曲线冷却段吻合也较好，为风速调整、码砖方式和孔隙率的选择提供了理论依据，提高了烧成质量和生产效率。

关键词：隧道窑冷却带；流-固耦合；散热；数值模拟

E-mail:xuning196402@163.com

0　引 言

隧道窑是现代化的连续式烧成的热工设备，广泛用于砖块和陶瓷产品的焙烧生产，烧结砖隧道窑冷却带在烧成带之后，主要的作用是使焙烧好的砖块迅速冷却。经常在窑尾安装风机，通过改变风速的大小从而控制砖块冷却的速率与温度。砖块内部传热机理是比较复杂的，涉及流相及固相的热传导和对流换热［1］。砖块上下温差受冷却风影响较大，出砖时砖块表面容易产生大的裂纹，影响砖块的质量。

随着微型计算机技术的发展以及计算方法的不断更新进步，计算机应用于烧结砖隧道窑冷却带的三维流-固耦合数值模拟成为现实。有关流固耦合的计算方法大致可以分为两类：一类是解析解；一类是数值解。数值解法通常采用的是有限单元法或有限差分法。Anton is Antoniou等人计算了二维流-固耦合流场［2］。梅国栋等采用有限差分法分析三维流-固耦合问题［3］。浙江大学李迎博士建立了内燃机活塞组-缸套-冷却水-机体流固耦合系统。对柴油机稳态工况下的耦合传热、周期性瞬态传热以及冷启动、外特性的瞬态传热与流动进行了数值仿真［4］。Ed Bendel主要通过测量排气管道表面的温度值作为边界条件进行数值模拟，并且利用Rad Therm和Star-CD的方法来分析对流、传导的换热特性［5］。刘上在FLUENT软件平台上，采用气固耦合传热计算的方法模拟了二维扩散燃烧实验器中的温度、组分分布［6］。大连理工大学周禛建立了单缸的缸盖- 缸套 - 冷却水耦合传热模型并且进行了耦合传热仿真［7］。

本文运用FLUENT软件对隧道窑冷却带流-固耦合散热进行数值模拟。模拟不同的风速、孔隙率、气体流动的数学模型以及砖块码放方式对隧道窑散热的影响。为砖块的散热找到最佳的风速、孔隙率、数学模型以及码砖的方式。为降低砖块的裂缝，提高砖块的质量寻找有效途径。

1　隧道窑冷却带的物理模型

在GAMBIT中建立了隧道窑冷却带的物理模型。为了减少计算量，提高运算效率对模型进行适当的简化，选取六节窑车进行流-固耦合散热的数值模拟。隧道窑冷却带的截面宽度为Y=3600 mm，窑车顶面到窑顶之间的距离Z=1200 mm，冷却带的长度为X=8000 mm。对模型进行假设：冷却带要求保温性良好；窑壁可以假设为绝热；窑尾的风机可以简化为速度入口；出口设为压力出口；不考虑砖块之间的传热影响以及砖垛之间的辐射传热影响。

图1　隧道窑冷却带的物理模型Fig.1 Physical model of the tunnel kiln cooling zone

隧道窑冷却带的物理模型分为砖块区、流体区。根据数值模拟要求采用Tet/Hybrid混合网格划分方法，即结构网格和非结构网格相结合的划分方法。对砖块区的网格划分，格间距为4，流体区的网格划分格间距为6。总计网格总数为670155。检查网格质量确保minimum volume不为负数。采用有限体积法对控制方程进行离散化，动量方程和能量方程用一阶迎风格式，迭代直至收敛。合理的划分网格有利于减少计算时间节约计算成本。

2　隧道窑冷却带的数学模型

本文计算中运用的控制方程为三维常物性不可压缩流动的连续性方程及能量方程。计算域为砖块与空气、粉尘流动的区域。

2.1标准的k-ε模型

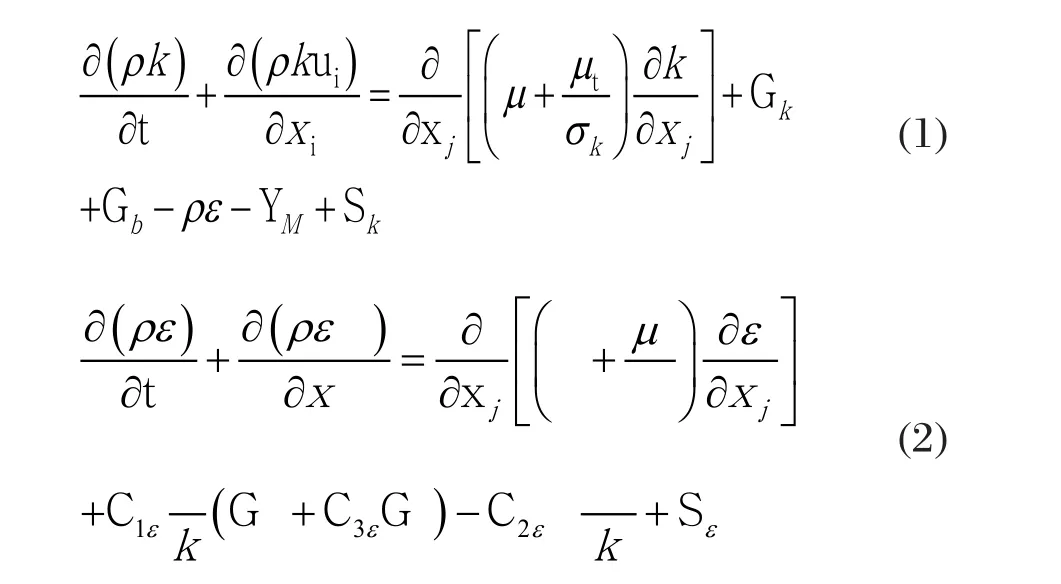
式中，Gk是由于平均速度梯度引起的湍动能产生；Gb是由于浮力影响引起的湍动能产生；YM为可压缩湍流脉动膨胀对总的耗散率的影响；C1ε、C2ε、C3ε为经验常数，FLUENT中默认值为C1ε=1.44、C2ε=1.92、C3ε=0.09；σk=1.0、σε=1.3。

2.2流固耦合控制方程简化

隧道窑冷却带内气体的流动看做粘性不可压缩的湍流流动。它在流动与传热的过程中遵循三大守恒方程：质量守恒方程、动量守恒方程（N-S方程）、能量守恒方程。

质量守恒方程

最后在求解过程中采用非耦合隐式格式（即SIMPLE算法）。该算法占用的内存小，计算快捷灵活。用有限容积法导出的离散方程可以保证具有守恒特性，而且离散方程系数的物理意义明确，是目前流动与传热问题的数值计算中应用最广的一种方法。

2.3模型边界条件及参数设定

在对隧道窑冷却带三维流固耦合散热数值模拟的研究中，将流体的进口设置为速度入口，流体初始速度方向要与源面垂直；流体的出口设定为压力出口［8-10］；隧道窑的窑壁在整个计算的过程中设为绝热壁；内部窑壁与砖块的区域设为流体区域［11］，流体不可压缩，流体中有气相和固相，将固相中的颗粒假设为密度相同直径均匀的颗粒［12］，忽略粒子之间的相互作用。砖块的密度为2500 kg/m3，导热系数为80 w/m.k，热生成率为0.57。

3　数值模拟结果与分析

3.1隧道窑冷却带流-固耦合温度场分布

根据FLUENT软件数值模拟计算经验，流体从隧道窑窑尾以5 m/s左右的速度进入，进入窑内流体的温度为常温。

图2是从窑长方向取得XY截面，从图中可以看出，颜色越深代表温度越高，气体从窑尾进入对砖块进行冷却，砖块运动的方向与气体运动方向相反，散热温度随窑车运动的方向逐渐降低。截面内温度分层情况比较均匀，砖块的左右平均温差不超过42 ℃。且在砖垛与窑壁之间或者砖垛与砖垛之间的间隙冷却的速度较快，主要因为砖垛与窑壁或者砖垛与砖垛之间的阻力较小气体流速较快。

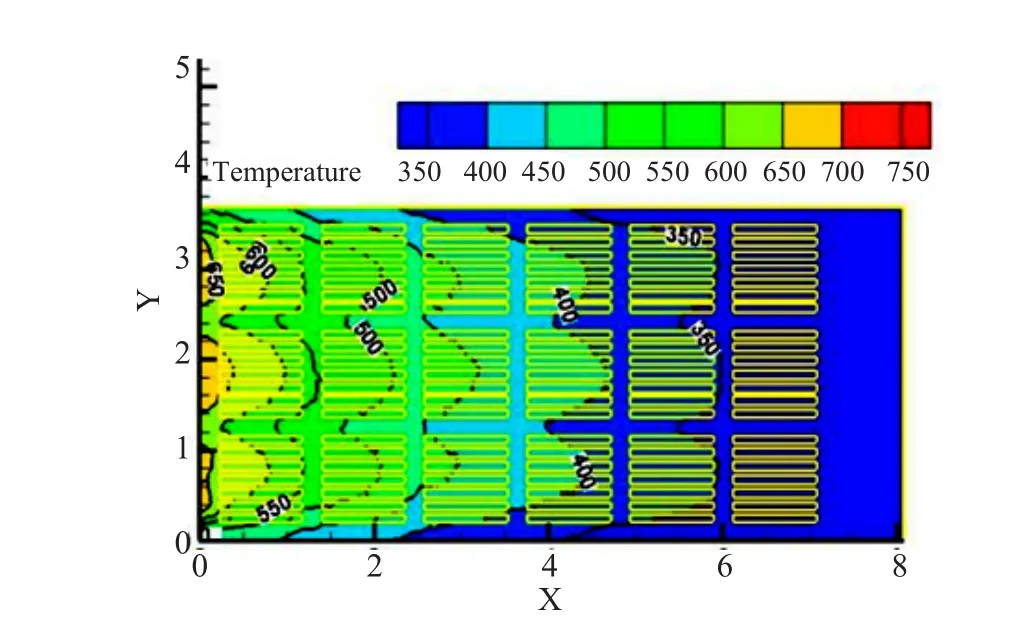
图2　Z=0.5m截面温度场分布图Fig.2 Temperature feld distribution on the cross-section of Z = 0.5 m

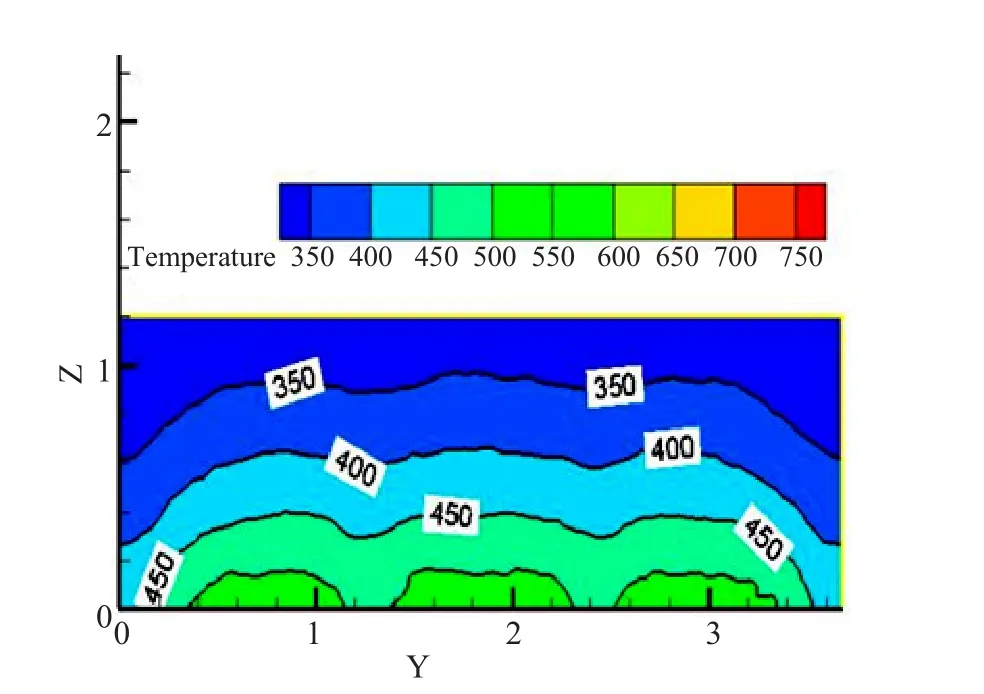
图3　X=3.6m截面温度场分布图Fig.3 Temperature feld distribution on the cross-section of X = 3.6 m

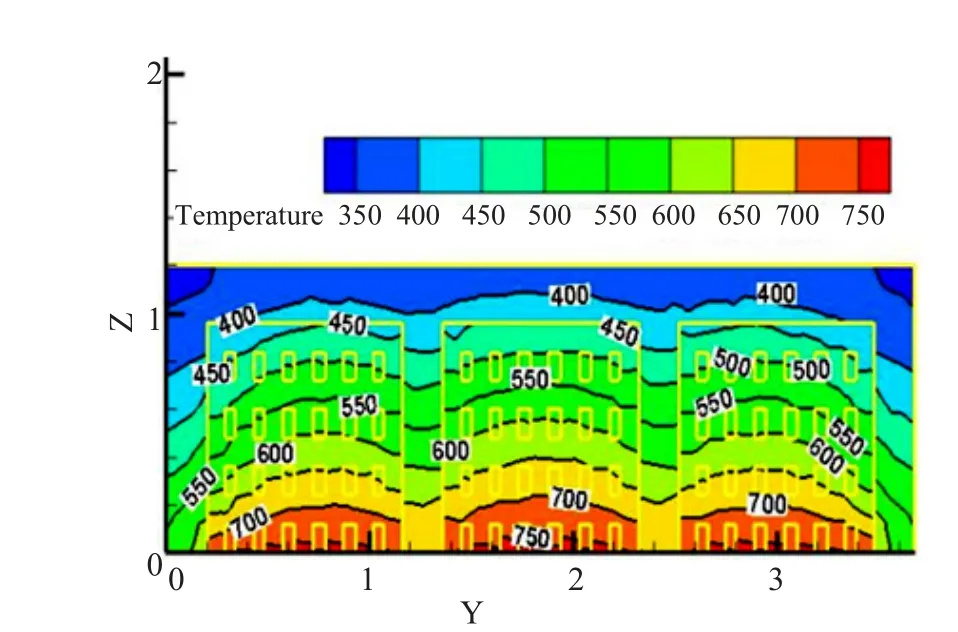
图4　X=0.8m　截面温度场分布图Fig.4 Temperature feld distribution on the cross-section of X = 0.8 m

图3、图4分别是沿着窑宽方向取得两个YZ截面。图5是沿着窑长方向取得XZ截面。从图中都可以看到窑顶的温度要比窑车台面的温度低，温度的变化梯度均匀。气体从窑体进入砖垛时速度会加大，这是由于进入窑体的风速为5 m/s，马赫数小于0.2可以认为气体的流动是低速，不考虑气体的压缩性，气体的速度与截面积成反比。气体进入砖垛时截面积变小则速度增大。气体与固相边界（即：砖垛）相互流动时还会产生湍流。在整个流-固耦合散热的过程中，砖垛附近产生较强的湍流影响冷却速度，在砖垛与窑顶之间主要是层流，冷却的速度较快，则出现窑顶的温度要比窑车台面附近区域的温度低。

3.2计算结果分析

为了研究不同风速对砖块的平均温度和上下温差影响。选择了10组不同风速进行数值模拟，计算残差取为10-3，在计算迭代过程中，当监测点的温度呈现稳定不变或者近似稳定不变时，即认为收敛。对比结果如下：

从图6可以看出，要保证隧道窑冷却带砖块冷却的温度与速度，同时还要保持窑内截面的温差最小，就要控制进入窑尾冷却风的风速。风速过低（风速小于5 m/s）时，随着气体流速升高温度逐渐降低，截面上下温差也在逐渐降低。风速达到5 m/s时，气体与砖垛达到产生湍流的条件，此时截面的上下温差达到最低。风速继续增加时，湍流的强度也随着风速增加逐渐降低，此时砖垛附近区域的散热平均温度下降逐渐变缓，截面的上下温差也在不断的增大。

从图7可以看出，孔隙率不断增大，砖块码放逐渐变得稀疏。Z=0.5 m时，XY截面的平均温度逐渐降低。XY截面的上下温差先减小后增大再减小的过程，主要是因为孔隙率小于0.5时，随着孔隙率的逐渐增加流体与砖垛的相互流动时还没有产生湍流，温差还在逐渐减小。当孔隙率在0.5-0.7之间时，湍流逐渐形成并且逐渐加强，影响散热温差也在逐渐增大。当孔隙率大于0.7时，砖块已经很稀疏，湍流现象逐渐消失，截面的温差也在逐渐降低。但考虑生产的产量与成本选取孔隙率为0.5较为合适。

从图8可以看出，二种不同气体的流动模型冷却曲线与隧道窑烧成曲线冷却段曲线对比结果，两条冷却曲线都与隧道窑烧成曲线冷却段曲线接近，但采用模型方式对砖块进行冷却曲线更接近隧道窑冷却曲线。主要因为气体在砖垛内流动的方式还是湍流，同时在做数值模拟时对物理模型和数学模型都进行了适当的简化，边界条件以及参数设定与实际有点差别，计算的方法也不够完善。

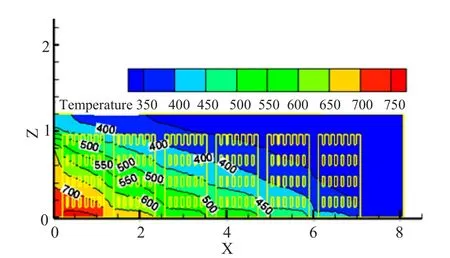
图5　Y=1.7m　截面温度场分布图Fig.5 Temperature feld distribution on the cross-section of Y = 1.7 m

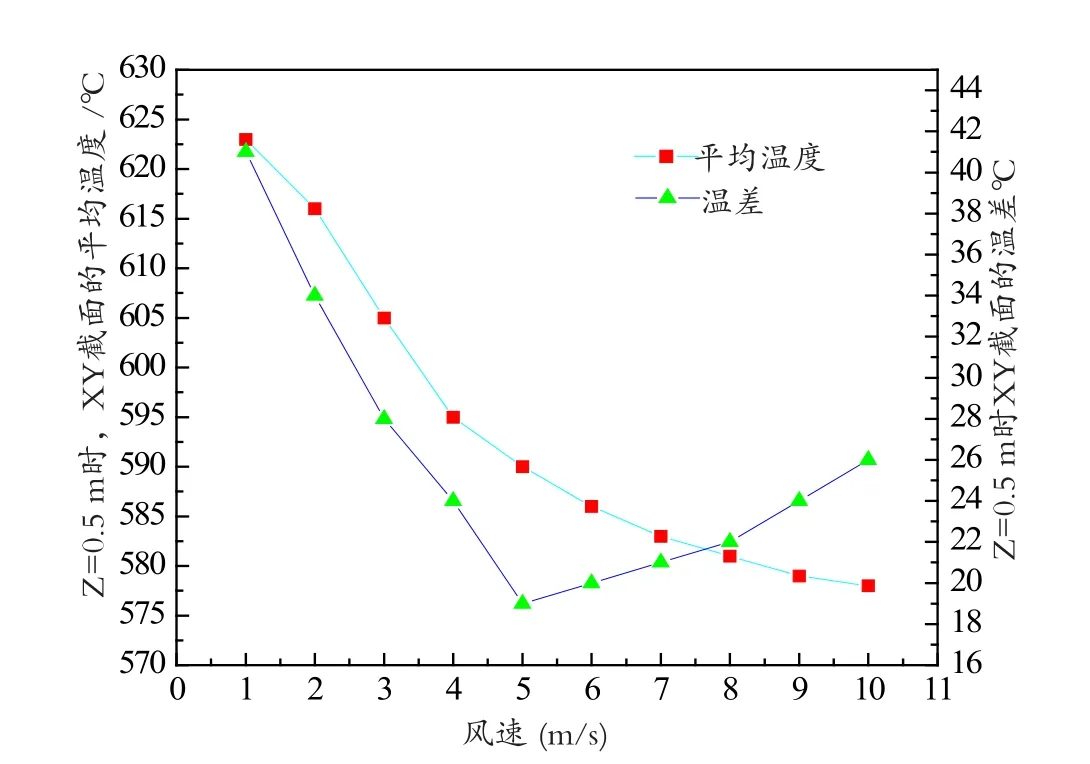
图6　Z=0.5m时不同风速对XY截面平均温度和温差的影响Fig.6 Effect of different draft speed on average temperature and temperature difference on XY cross-section when Z = 0.5 m

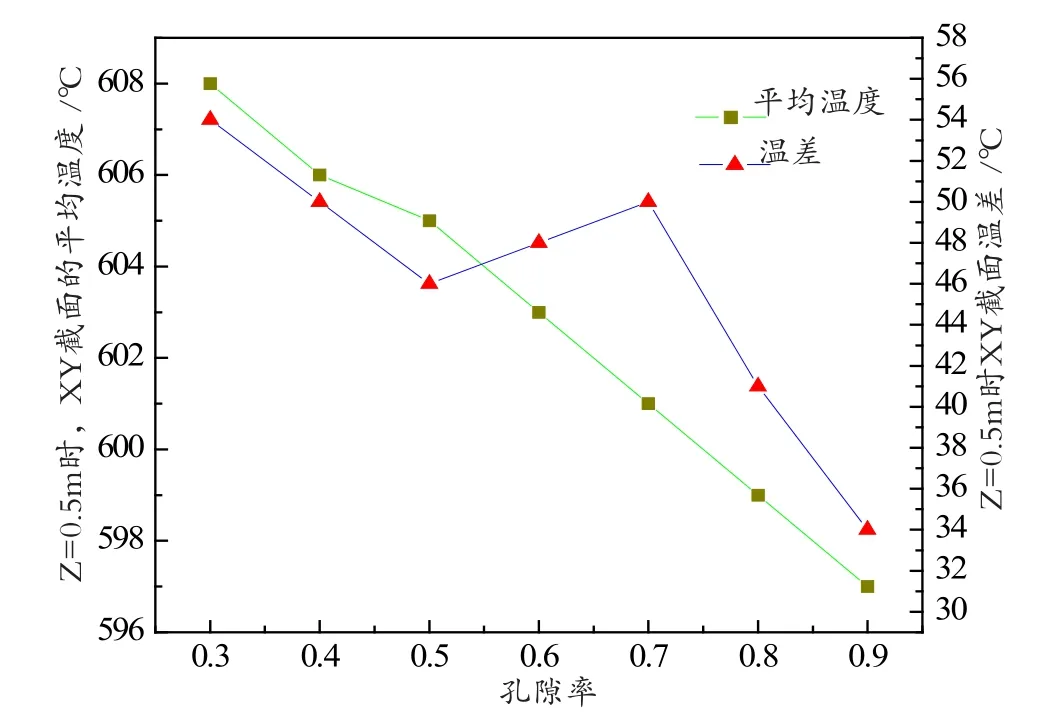
图7　Z=0.5m时不同孔隙率对XY截面平均温度和温差的影响Fig. 7 Effect of different pore rate on average temperature and temperature difference on XY cross-section when Z = 0.5 m

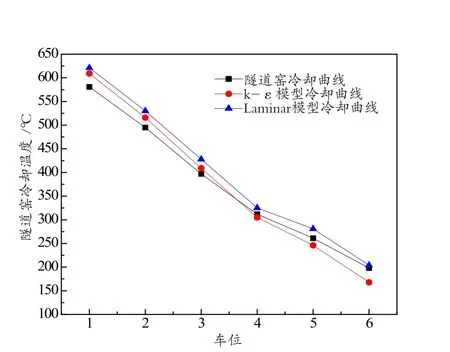
图8　不同气体流动模型冷却曲线与隧道窑烧成曲线冷却段对比Fig.8 Contrast of the cooling curves of different fuid-fow models with the cooling segment of the tunnel kiln fring curve

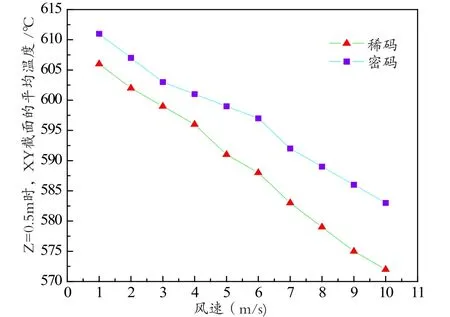
图9　不同码放方式对砖块散热温度变化的影响Fig.9 Effect of different bricks arrangement on brick heat transfer

从图9可以看出，随着风速加快Z=0.5 m的XY截面平均温度下降，在相同风速、孔隙率下砖块稀码比砖块密码的平均温度低。从图中曲线下降的斜率可以看出：砖块稀码温度随着风速下降的速度快于砖块密码。主要因为砖块稀码时，气体与砖垛接触面积加大，温度降低速度也会加快，平均温度也会相对较低。砖块稀码时气体在砖垛内部的湍流强度小于砖块密码，其散热效果也要优于砖块密码。

4　结 论

本文运用FLUENT对隧道窑冷却带六节窑车段进行流-固耦合散热数值模拟，结论如下：

（1）用数值模拟的方法对隧道窑冷却带砖块的散热进行模拟，可以代替大量的反复实验，节约大量的人力物力缩短研究时间。

（2）文中分别从风速、孔隙率、码砖方式的角度展开研究。研究表明：风速5 m/s，孔隙率0.5时砖块散热时上下温差较小，平均温度较低；在相同风速与孔隙率的条件下砖块稀码比砖块密码的散热条件好。

（3）选择合适的数学计算模型可以有效的模拟隧道窑冷却带散热的过程，为以后的实验研究提供理论依据。

（4）文中的散热数值模拟均基于实际生产条件，模拟的结果与实际数据相吻合，表明文章中数值模拟的结果是可行的，接下来进一步的工作将模拟的结果应用于实际生产中，针对生产的实际情况做适当的调整。

参考文献：

［1］ 百敏丽， 薛莹莹， 吕继祖， 等. 隔热材料导热系数的数值模拟预测［J］. 热科学与技术， 2007， 6（2）： 136-140.

［2］ AKYUZLU K M， ANTONIOU A. Determination of regression rate in an ablation hybrid rocket solid fuel using a physics based comprehend div mathematical model. AIAA， 2002： 2002-3577. ［3］ 梅国栋， 王云海. 三维流固耦合数值模拟在铜锣山隧道安全性评价中的应用［J］. 中国安全生产科学技术， 2009， 5（6）： 57-61. ［4］ 李迎. 内燃机流固耦合传热问题数值仿真与应用研究［D］. 浙江大学， 2006.

［5］ BENDELL E. Investigation of a coupled CFD and thermal modeling methodology for prediction of vehicle underbody temperature. SAE， 2005-01-2044.

［6］ 刘上， 孙得川. 固液发动机实验燃烧器的气固耦合传热计算［J］. 推进技术， 2008， 29（3）： 258-261.

［7］ 周禛， 薛冬新， 唐斌， 等. 某中速柴油机冷却液流动及流固耦合传热计算分析［J］. 柴油机， 2013， 35（1）： 17-32.

［8］ KAYA S， MANCHAN E. Modelling and optimization of the firing zone of a tunnel kiln to predict the optimal feed locations and mass fluxes of the fuel and secondary air. Applied Energy，2009， 86： 325-332.

［9］ NICOLAU V P， DADAM A P. Numerical and experimental thermal analysis of a tunnel kiln used in ceramic production. Journal of the Brazilian Society of Mechanical Sciences & Engineering 2009， 31 （4）： 297-304.

［10］ SANTOS G M. Study of thermal behavior of a tunnel kiln used in red ceramic industry. Master Thesis， Federal University of Santa Catarina， Santa Catarina， Brazil， 2001.

［11］ NACCACHE M F， GOMES M S P. Numerical simulation of flow and heat transfer through a tunnel kiln. 18th International Congress of Mechanical Engineering， November 6-11， 2005.

［12］ OBA R， POSSAMAI T S. Thermal analysis of tunnel kiln used to produce roof tiles. Applied Thermal Engineering， 2013. 63（1）： 59-65.

通信联系人：许宁，男，博士，教授。

Received date:2015-12-18. Revised date: 2015-12-20.

Correspondent author:XU Ning， male， Ph.D.， Professor.

Numerical Simulation of Fluid - Solid Coupling Heat Transfer in Tunnel Kiln Cooling Zone

XU Ning1， 2， Wang Xuefeng1， 2， ZHANG Zhuyin2， WANG Jun2， HUANG Janjun1， XIAO Hui3， ZHI Xiao4
（1. School of Mechanical Engineering， Yancheng Institute of Technology， Yancheng 224051， Jiangsu， China； 2. School of Mechanical Engineering， Hunan University of Technology， Zhuzhou 412007， Hunan， China； 3. Xi'an Research & Design Institute of Wall & Roof Materials， Xi'an 710061， Shaanxi， China； 4. China National Materials Group Corporation， Beijing 100036， China）

Abstract:In order to obtain the cooling temperature feld data in the tunnel kiln cooling zone， the tunnel kiln wall bricks-fuid coupling heat transfer physical model and mathematic model were established， taking a sintered brick tunnel kiln as the research object. The tunnel kiln wall bricks-fuid coupling heat transfer simulations were performed by commercial software FLUENT， and the overall accurate intuitive temperature feld distribution was obtained. The simulation results show: the cooling effect on the tunnel kiln cooling zone is better when the draft speed is 5 m/s， the pore rate is 0.5， and the bricks arrangement is sparse， and that is also agreeable with the tunnel kiln fring curve's cooling segment. This information provides a theoretical basis for the adjustment of the draft speed， pore rate and bricks arrangement to improve the quality of bricks fring and productivity.

Key words:tunnel kiln cooling zone； fuid - solid coupling； heat transfer； numerical simulation

基金项目：国家科技支撑项目水泥、墙材窑炉大气污染治理关键技术研究与示范（2013BCA13B01）；湖南省自然科学基金资助项目（13JJ9034）；江苏省新型环保重点实验室资助项目（AE201109）。

收稿日期：2015-12-18。

修订日期：2015-12-20。

DOI:10.13958/j.cnki.ztcg.2016.02.006

中图分类号：TQ174.6+53

文献标志码：A

文章编号：1006-2874（2016）02-0026-05