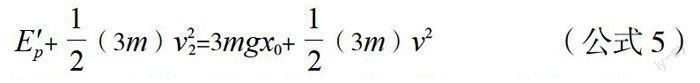“对称”法巧解动量与机械能双守恒问题

摘 要：随着物理研究的不断深入，许多新的物理现象被挖掘与发现出来，为世界科学的发展做出巨大的贡献。如两个物体之间产生了碰撞且发生了机械能守恒，在这个过程被称之为弹性碰撞，在近代物理学上经常会汲及微观粒子的碰撞。微观粒子产生碰撞的过程并不会有能量的损失，因此，微观粒子与其他物体的碰撞及机械能守恒是当文章研究的重点，文章以解题的形式进行动量与机械能双守恒问题的解释。

关键词：对称法；巧解运量；机械能守恒

一、对称法在动能定理中应用技巧

例1：一个物体从斜面上高h处由静止滑下并紧接着在水平面上滑行一段距离后停止，测得停止处对开始运动处的水平距离为S，不考虑物体滑至斜面底端的碰撞作用，并设斜面与水平面对物体的动摩擦因数相同.求动摩擦因数μ.

解析：设该斜面倾角为α，斜坡长为l，则物体沿斜面下滑时，重力和摩擦力在斜面上的功分别为：

WG=mglsinα=mgh

Wf1=-μmglcosα

物体在平面上滑行时仅有摩擦力做功，设平面上滑行距离为S2，则Wf2=-μmgS2

对物体在全过程中应用动能定理：ΣW=ΔEk.所以：

mglsinα-μmglcosα-μmgS2=0，得到：h-μS1-μS2=0

在公式中S1代表斜面底端与物体初位置间的水平距离，从而有：

一个物体的动能变化ΔEk与合外力对物体所做的总功具有等量代换关系.若ΔEk>0，表示物体的动能增加，其增加量等于合外力对物体所做的正功；若ΔEk<0，表示物体的动能减少，其减少量等于合外力对物体所做的负功的绝对值；若ΔEk=0，表示合外力对物体所做的功为0，反之亦然。这种等量代换关系提供了一种计算变力做功的简便方法。动能定理中涉及的物理量有F、s、m、v、W、Ek等。

二、动能定理解题的基本思路

例2：如图1所示，AB为1/4圆弧轨道，半径为R=0.8m，BC是水平轨道，长S=3m，BC处的摩擦系数为μ=1/15，今有质量m=1kg的物体，自A点从静止起下滑到C点刚好停止.求物体在轨道AB段所受的阻力对物体做的功.

解析：物体在从A滑到C的过程中，有重力、AB段的阻力、BC段的摩擦力共三个力做功，WG=mgR，fBC=umg，由于物体在AB段受的阻力是变力，做的功不能直接求.根据动能定理可知：W外=0，所以有

mgR-umgS-WAB=0

即

WAB=mgR-umgS=1？10×0.8-1？10×3/15=6J

三、机械能守恒定律

机械能守恒定律分为两个部分，一个为守恒内容，另一个为守恒条件，详细解释如下：

机械能守恒内容：在只有重力或弹力做功的物体系统内，动能与重力势能可以相互转化，而总的机械能保持不变.

机械能守恒条件：在重力或弹力做功下，地发生动能和势能的转化.对一个物理过程的分析不仅仅是满足机械能守恒，最重要的是分析产生的过程中，有哪些力参与了做功，且做功是怎么形式的转化成能，若仅仅是动能和势能的转化，而示发生其它形式的能的转化，则是机械能守恒，若力示参与做功，则不会发生能的转化，机械能也不存在。

四、机械能守恒定律解题的步骤

例3：如图2所示，光滑的倾斜轨道与半径为R的圆形轨道相连接，质量为m的小球在倾斜轨道上由静止释放，要使小球恰能通过圆形轨道的最高点，小球释放点离圆形轨道最低点多高？通过轨道点最低点时球对轨道压力多大？

解析：小球在运动过程中，受到重力和轨道支持力，轨道支持力对小球不做功，只有重力做功，小球机械能守恒.取轨道最低点为零重力势能面.

因小球恰能通过圆轨道的最高点C，说明此时，轨道对小球作用力为零，只有重力提供向心力，根据牛顿第二定律可列

在圆轨道最高点小球机械能：

在释放点，小球机械能为：EA=mgh

根据机械能守恒定律EC=EA列等式：

同理，小球在最低点机械能

小球在B点受到轨道支持力F和重力根据牛顿第二定律，以向上为正，可列

据牛顿第三定律，小球对轨道压力为6mg，方向竖直向下。

例4：质量为m的钢板与直立轻弹簧的上端连接，弹簧下端固定在地上.平衡时，弹簧的压缩量为x0，如图3所示.物块从钢板正对距离为3x0的A处自由落下，打在钢板上并立刻与钢板一起向下运动，但不粘连，它们到达最低点后又向上运动.已知物体质量也为m时，它们恰能回到O点，若物块质量为2m，仍从A处自由落下，则物块与钢板回到O点时，还具有向上的速度，求物块向上运动到最高点与O点的距离，物块从3x0位置自由落下，与地球构成的系统机械能守恒。

则有：

v0为物块与钢板碰撞时的速度.因为碰撞板短，内力远大于外力，钢板与物块间动量守恒.设v1为两者碰撞后共同速

mv0=2 （公式2）

两者以v1向下运动恰返回O点，说明此位置速度为零。运动过程中机械能守恒。设接触位置弹性势能为Ep，则

同理2m物块与m物块有相同的物理过程

碰撞中动量守恒2mv0=3mv2 （公式4）

所不同2m与钢板碰撞返回O点速度不为零，设为v则

因为两次碰撞时间极短，弹性形变未发生变化

Ep=E′p （公式6）

由于2m物块与钢板过O点时弹力为零.两者加速度相同为g，之后钢板被弹簧牵制，则其加速度大于g，所以与物块分离，物块以v竖直上抛.上升距离为：

将1至6公式解得v代入最后7公式中可解得h=x0

本题主要考查了机械能守恒、动量守恒、能量转化及守恒等多个知识点，是一个多运动过程的问题。关键问题是分清楚每一个过程.建立过程的物理模型，找到相应解决问题的规律.弹簧类问题，提前画好位置草图十分重要.

五、结语

随着高中物理新课标的改革，学生在学习高中物理课程中的动量及机械能守恒时，学生应通常解题的方式进行练习，才能加深对题目的理解，在求解过程中寻找解题的兴趣，作为一名高中学生，物理知识的学习能够促进学生思维能力及构思能力，促进学生的全面的发展。

参考文献

[1] 周孝明，张敏.“对称”法巧解动量与机械能双守恒问题[J].中学物理（高中版），2015，33（03）：39-40.

[2] 张小洪.如何解动量与机械能双守恒的方程组[J].中学物理（高中版），2012，30（09）：71.

[3] 王杰，王梅華.机械能守恒定律在碰撞问题中的应用[J].黑龙江科技信息，2009（12）：32.

[4] 张敏.巧用类比法解答物理问题[J].数理化学习（高一二版），2013（01）：43.

作者简介：许浩然，海安高级中学。