纸带处理专题分析

刘清发

利用打点计时器打出纸带的目的是利用纸带上的点迹来分析物体的运动情况，然而在处理纸带的过程中，学生普遍感到处理起来比较困惑，比较混乱，现在把处理纸带的有关方法汇总如下，以便于大家掌握用纸带分析物体运动的情况这种基本技能.

一、逐差法

1.相邻逐差法

由于物体做匀变速直线运动，所以满足在连续相等的时间间隔内位移之差相等，即Δx=aT2，可解得a=ΔxT2.

例1 一打点计时器固定在倾角为θ的斜面上，一小车拖着穿过打点计时器的纸带从斜面上滑下，打出的纸带的一段如图1所示，纸带上0、1、2、3、4、5、6是按先后顺序打出的计数点，每相邻两个计数点之间还有四个实验点未画出.

（1）根据纸带上记录的数据判断小车是做

运动.

（2）若小车做匀加速运动，则加速度大小a

. （3）小车在计数点3所对应的速度大小为v=

图1解析

（1）x1=6.00 cm，

x2=16.00 cm -6.00 cm=10.00 cm，

x3=30.00 cm-16.00 cm=14.00 cm，

x4=48.00 cm-30.00 cm=18.00，

x5=70.00 cm-48.00 cm=22.00 cm，

x6=96.00 cm-70.00 cm=26.00 cm.

可得：Δx=x2-x1=x3-x2=x4-x3=x5-x4=x6-x5=4.00 cm，即相邻的相等时间内的位移之差为常数，所以可以判断物体做的是匀加速直线运动.

（2）每相邻两个计数点之间还有四个实验点未画出，所以相邻的计数点间的时间间隔 T=0.1 s， 根

据匀变速直线运动的推论公式Δx=aT2得，a=ΔxT2=0.040.12m/s2=4 m/s2.

（3）根据匀变速直线运动中时间中点时刻的速度等于该过程中的平均速度，所以v=x3+x42T=1.6 m/s.

例2 在做“探究小车速度随时间变化的规律”的实验中，取一段如图2所示的纸带研究其运动情况.设O点为计数的起始点，在四个连续的计数点中，相邻计数点间的时间间隔为0.1 s，若物体做理想的匀加速直线运动，则计数点“A”与起始点O之间的距离x1为

cm，打计数点“A”时物体的瞬时速度为

m/s，物体的加速度为

m/s2.

图2解析 根据匀变速直线运动的特点（相邻的时间间隔位移之差相等）得出： xBC-xAB=xAB-x1.解得计数点A与起始点O之间的距离为x1=4.00 cm.

根据匀变速直线运动中时间中点时刻的速度等于该过程中的平均速度，可以求出打计数点“A”时物体的瞬时速度为：vA=0.100.2m/s2=0.50 m/s.根据匀变速直线运动的推论公式Δx=aT2得，a=ΔxT2=0.020.12m/s2=2.00 m/s2.

2.隔项逐差法

从理论上来说，由于物体做匀变速直线运动，所以满足在连续相等的时间间隔内位移之差相等，即Δx=aT2.但在实际的实验过程中不可避免的出现或多或少的误差，造成相邻时间内的位移差测量的并不相等，如果再利用一个Δx求解加速度，偶然误差务必太大，为了减小实验中的偶然误差，分析纸带时，纸带上的各段位移最好都用上，如图3纸带上测得连续6个相同的时间间隔T内的位移x1、x2、x3、x4、x5x6，则x4-x1=（x4-x3）+（x3-x2）+（x2-x1）=3a1T2，同理，x5-x2=3a2T2，x6-x3=3a3T2，物体的加速度a=a1+a2+a33=（x4-x1）+（x5-x2）+（x6-x3）9T2=（x4+x5+x6）-（x1+x2+x3）9T2.由此可以看出，各段位移都用上了，有效地减小了偶然误差，这种方法被称为逐差法.所以利用纸带计算加速度时，应使用逐差法.

图3例3 某学生用打点计时器研究小车的匀变速直线运动.他将打点计时器接到频率为50Hz的交流电源上，实验时得到如图4的一条纸带.他在纸带上便于测量的地方选取第一个计时点，在这点下标明A，第六个点下标明B，第十一个点下标明C，第十六个点下标明D，第二十一个点下标明E.测量时发现B点已模糊不清，于是他测得AC长为14.56 cm、CD长为11.15 cm、DE长为13. 73 cm，则打C点时小车的瞬时速度大小为

m/s，小车运动的加速度大小为

m/s2， AB的距离应为

cm.（保留三位有效数字）

图4解析 在第一个点下标明A，第六个点下标明B，第十一个点下标明C，第十六个点下标明D，第二十一个点下标明E；可以看出相邻的计数点间的时间间隔为T=0.02×5 s=0.1 s.根据匀变速直线运动中时间中点时刻的瞬时速度等于该过程中的平均速度，可以求出打纸带上C点时小车的瞬时速度大小，vC=AC+CD+DE4T=0.986 m/s.由逐差法可得：a=CE-AC4T2=2.58 m/s2.根据逐差相等得，xBC-xAB=xDE-xCD=13.73 cm-11.15 cm=2.58 cm，又因为xBC+xAB=xAC=14.56 cm，解得xAB=5.99 cm.

点评 所谓逐差法，就是把测量的数据逐项相减或按顺序分为两组进行对应项相减，然后将所得差值作为因变量的多次测量值进行数据处理的方法.它也是物理实验中处理数据常用的一种方法.

二、 v-t图象法

例4 某学生在做“探究小车运动的速度与时间关系”的实验中选择了一条清晰的纸带，在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图5所示，每两个相邻的计数点之间还有四个点未画出.

图5（1）根据纸带上各个计数点间的距离，计算出打下B、C、D、E、F五个点时小车的瞬时速度，请将vC、vE的速度值填入下表（要求保留3位有效数字）

（2）将B、C、D、E、F各个时刻的瞬时速度标在如图6甲所示的坐标纸上，并画出小车的瞬时速度随时间变化的关系

（3）根据第（2）问中画出的v-t图线，求出小车运动的加速度为

m/s2.（保留两位有效数字）甲 乙

图6解析 （1）每两个相邻的计数点之间还有四个点未画出，所以两个相邻的计数点之间的时间间隔为0.10 s.根据在匀变速直线运动中时间中点时刻的瞬时速度等于该过程中的平均速度可以求出各点的瞬时速度大小.vC=xBD2T=4.38+5.202×0.1cm/s=0.479 m/s，vE=xDF2T=5.99+6.802×0.1cm/s=0.640 m/s.

（2）以开始打A点时为计时起点，每隔0.15秒选一个点，适当的选取纵横数值，根据表格中所给出的各个点速度大小，用描点法即可画出速度-时间图象如图6乙所示.

（3）根据图象的物理意义可知，在速度-时间图象中，图象的斜率大小表示物体的加速度大小，故a=ΔvΔt=0.80 m/s2.

点评 （1）利用纸带进行计算，要注意三点：①计数点是如何取的；②长度采用了什么单位；③所给的纸带数据是谁与谁之间的距离.

（2）做v一t图线时，要使描得的点尽可能的分布在直线的两侧，偏差过大的点不予考虑.

（3）由a=ΔvΔt求a时，要在图线上取两个相对较远的点.

三、贴纸法

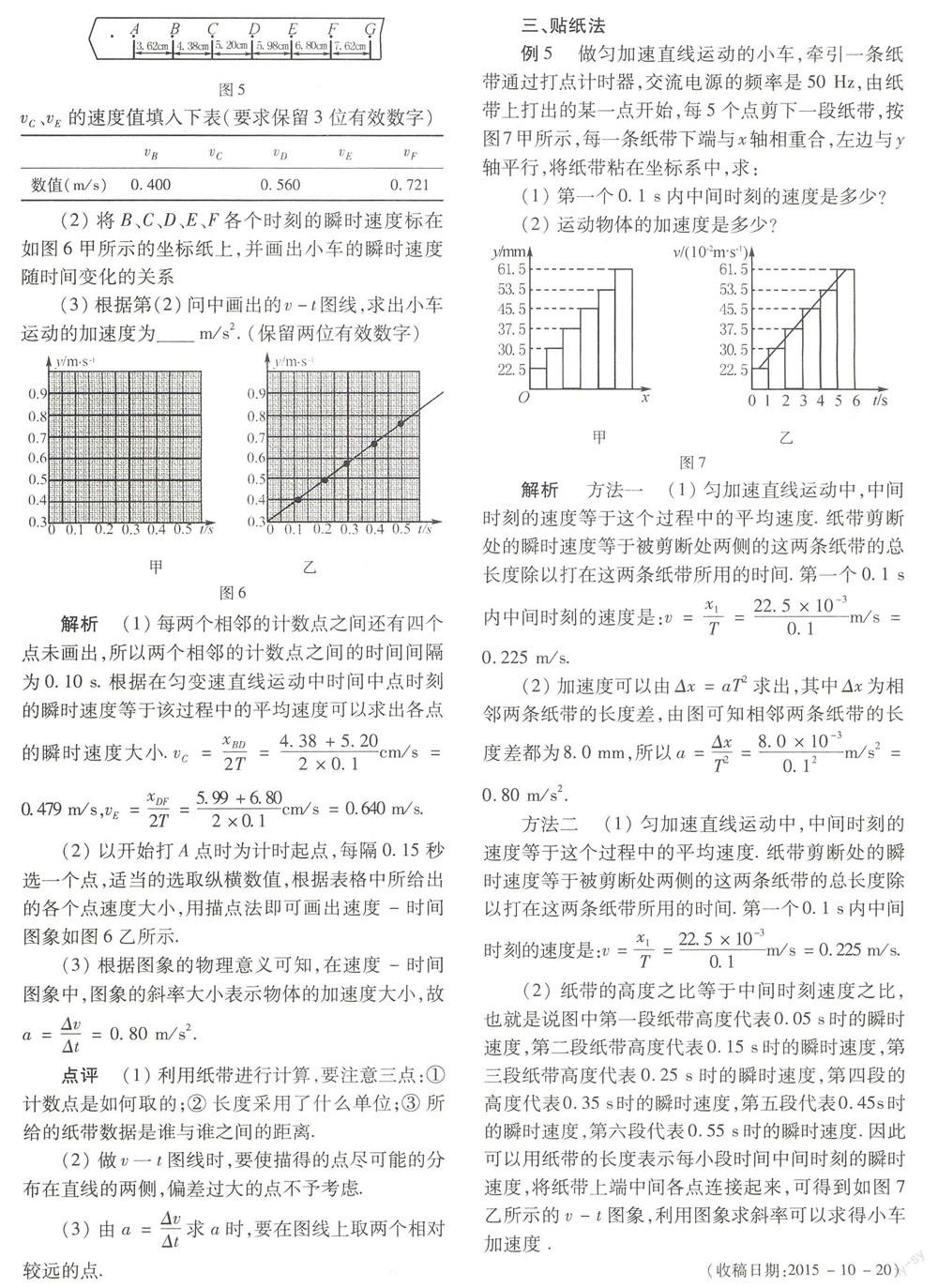
例5 做匀加速直线运动的小车，牵引一条纸带通过打点计时器，交流电源的频率是50 Hz，由纸带上打出的某一点开始，每5个点剪下一段纸带，按图7甲所示，每一条纸带下端与x轴相重合，左边与y轴平行，将纸带粘在坐标系中，求：

（1）第一个0.1 s内中间时刻的速度是多少？

（2）运动物体的加速度是多少？

甲 乙

图7解析 方法一 （1）匀加速直线运动中，中间时刻的速度等于这个过程中的平均速度.纸带剪断处的瞬时速度等于被剪断处两侧的这两条纸带的总长度除以打在这两条纸带所用的时间.第一个0.1 s内中间时刻的速度是：v=x1T=22.5×10-30.1m/s=0.225 m/s.

（2）加速度可以由Δx=aT2求出，其中Δx为相邻两条纸带的长度差，由图可知相邻两条纸带的长度差都为8.0 mm，所以a=ΔxT2=8.0×10-30.12m/s2=0.80 m/s2.

方法二 （1）匀加速直线运动中，中间时刻的速度等于这个过程中的平均速度.纸带剪断处的瞬时速度等于被剪断处两侧的这两条纸带的总长度除以打在这两条纸带所用的时间.第一个0.1 s内中间时刻的速度是：v=x1T=22.5×10-30.1m/s=0.225 m/s.

（2） 纸带的高度之比等于中间时刻速度之比，也就是说图中第一段纸带高度代表0.05 s时的瞬时速度，第二段纸带高度代表0.15 s时的瞬时速度，第三段纸带高度代表0.25 s时的瞬时速度，第四段的高度代表0.35 s时的瞬时速度，第五段代表0.45s时的瞬时速度，第六段代表0.55 s时的瞬时速度.因此可以用纸带的长度表示每小段时间中间时刻的瞬时速度，将纸带上端中间各点连接起来，可得到如图7乙所示的v-t图象，利用图象求斜率可以求得小车加速度 .

（收稿日期：2015-10-20）