战胜有理数

张伟

一、知识点

1.有理数的意义：数轴、相反数、倒数、绝对值、近似數与有效数字.

2.有理数的运算：加减乘除、乘方、有理数的大小比较、科学记数法.

二、中考知识梳理

1. 有理数的有关概念

要准确把握有理数的概念，特别是负数和绝对值的概念是难点，要深刻理解，并结合数轴理解这两个概念.用数形结合的思想，使抽象的概念具体化，还有近似数的有效数字的概念也是非常重要的，要理解透彻.

2. 有理数的运算

灵活运用有理数的运算法则、运算律、运算顺序以及有理数的混合运算，利用运算律简化运算要熟练掌握.运算中的符号问题是易出错的地方，要特别注意.还要掌握好减法转化成加法，除法转化成乘法这种转化思想.

题型一 有理数的概念问题

1. 整数、0、负整数、正分数、负分数都可以写成分数的形式，这样的数称为有理数.

注：（1）正整数、0、负整数统称为整数.

（2）正分数和负分数统称为分数.

（3）对于小数，只有能化成分数的小数才是有理数.

（4）我们把有限小数和无限循环小数都看作分数，因此有限小数和无限循环小数是有理数.

（5）无限不循环小数不能化成分数，因此它不是分数，也不是整数，所以就不是有理数.

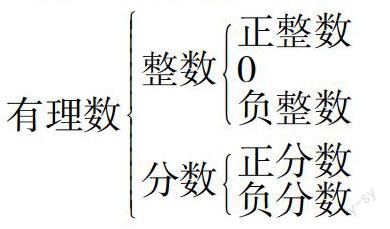
2. 有理数的分类（重点）

按有理数的种类分：

有理数整数正整数0负整数分数正分数负分数

按有理数的性质分：

有理数正有理数正整数正分数0负有理数负整数负分数

注：（1）有理数的分类必须按同一标准，不漏、不重.

（2）0和正整数统称为非负整数.

（3）0和负整数统称为非正整数.

（4）0和正有理数统称为非负数.

（5）0和负有理数统称为非正数.

例1：（2015年 山东省威海市）检验4个工件，其中超过标准质量的克数记作正数，不足标准质量的克数记作负数.从轻重的角度看，最接近标准的工件是（ ）.

A.-2 B.-3 C. 3 D. 5

考点：正数和负数.

分析：根据正负数的意义，绝对值最小的即为最接近标准的.

答案：A.

点评：此题主要考查了正负数的意义，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量.一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示.

？笠题型二 利用数轴解决问题

1. 数轴的定义：规定了原点、正方向、单位长度的直线叫做数轴.画数轴时，要注意上述规定的三要素缺一不可.

2. 解题时要真正掌握数形结合的思想，理解实数与数轴的点是一一对应的，并能灵活运用.①画一条水平直线，在直线上取一点表示0（原点），选取某一长度作为单位长度，规定直线上向右的方向为正方向，就得到数轴（“三要素”）.②任何一个有理数都可以用数轴上的一个点来表示. ③如果两个数只有符号不同，那么我们称其中一个数为另外一个数的相反数，也称这两个数互为相反数.

3. 数轴的作用： ①直观地比较有理数的大小； ②明确体现绝对值意义； ③建立点与实数的一一对应关系.

例2：（2015年 山东省威海市）已知实数a、b在数轴上的位置如图所示，下列结论错误的是（ ）.