例谈思想方法在数学复习中的渗透

周东

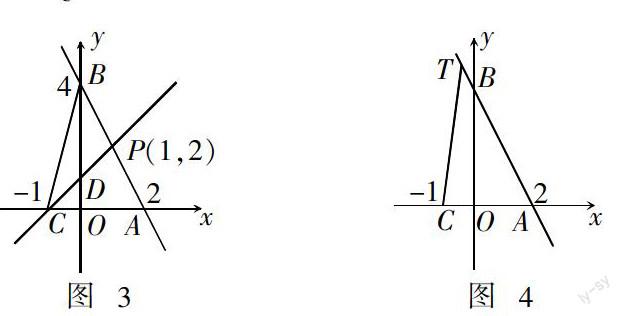
【摘要】初中数学复习课不能只停留在讲一题是一题的层面，要进一步提炼数学思想方法，培养学生用思想方法解题的能力，从而达到触类旁通的效果. 本文从八上复习《一次函数与三角形的面积》一课设计为例，谈在数学课堂上渗透数形结合、转化、分类讨论的思想方法.

【关键词】 数学；思想方法

当前，初中数学复习课堂多以解题教学为主线，解了一题又一题. 教师争取课堂密度大，多讲习题，学生也想把这些习题都听懂，这样的课堂学生忙教师苦，走进了数学教学的误区. 笔者认为在数学复习课教学中要对数学内容的进一步提炼和概括，总结出相对应的数学思想方法，数学思想方法是对数学内容的一种本质认识，有了数学思想为灵魂，数学才有了魅力. 因此，在复习时要注重体会教材例题、习题以及中考试题中所体现的数学思想和方法，培养用数学思想方法解决问题的意识.下面以八上期末复习《一次函数与三角形面积》为例，谈数学复习课堂如何注重培养学生数学思想与方法.

一、课前梳理，数形结合

著名数学家华罗庚说过：“数缺形时不直观，形少数时难入微”. 所谓数形结合是指抽象的数学语言与形象直观的图形结合起来，从而实现由抽象向具体转化的一种思维方式. 八上学生第一次接触函数存在一定的难度，笔者在课前梳理阶段做了如下设计，让学生独自完成体会数形结合思想.

1. 点A（3，-2）到x轴的距离是______，到y轴的距离是_______.

2. 直线y = -2x + 4与x轴交点A坐标______，与y轴交点B坐标______，△AOB的面积是______.

3. 直線y = -2x + 4与y = x + 1相交于点T，则点T的坐标为______.

4. 已知A（ 2， 0 ）、C （ -1，0），则AC = ______.

归纳：

1. 点P（a，b）到x轴的距离为______，到y轴的距离为______ .

2. 一次函数y = kx + b与x轴的交点坐标______，与y轴的交点坐标______.

3. 通过解方程（组）求交点坐标.

4. 点A（a，0）点B（b，0），A、B两点之间的距离为_____.

通过练习，让学生感受点的坐标一对有序实数和点的位置的关系，点的坐标到坐标轴距离之间的关系，为课堂学习打好基础.

二、层层深入，化繁为简

转化思想是解决数学问题的一种最基本的数学思想，在研究数学问题时，我们通常是将未知问题转化为已知的问题，将复杂的问题转化为简单的问题，从而提高同学们的解题能力. 在课堂复习中笔者设计如下几个环节：

（一）知识应用

如图（1），直线l：y = -2x + 4与x轴、y轴分别交于点A、B，直线y = x + 1与x轴、y轴分别交于点C、D，与直线l交点P.

（1）求△CAP的面积.

（2）你还能求出哪些三角形的面积？

（3）连接BC，求△BCP的面积.

让学生探索：有边在坐标轴上的三角形，利用在坐标轴上的（或平行于坐标轴）的线段为底. 第三问△BCP没有边在坐标轴上怎么办？利用割补法将三角形面积转化为有边在坐标轴上的（或平行于坐标轴）三角形面积和（差）.

（二）知识拓展

拓展一 如图，在直线y = -2x + 4上，取两点E（1/2，3），点F（3/2，3），求△EOF的面积（多种方法）.

通过充分的讨论交流，让学生概括总结求三角形面积的多种方法. 点拨概括：割补法可以将三角形面积转化为面积和或差，即向内分割和向外补形.

拓展二 如图（3）点Q在y轴上，且△QPB与△CPB面积相等，求点Q的坐标.

同样的问题背景，在求了三条直线围成的静态的三角形面积后，笔者设计了在y轴上的一个动点和原三角形面积相等问题，注重培养分类讨论的数学思想.

拓展三 如图（4），点T是直线AB： y = -2x + 4上的一个动点，连接CT.设T点横坐标为t.

（1）求△CAT的面积S与t的函数关系.

（2）当点T运动到什么位置时△CAT的面积为6.

把动点从坐标轴上改成在直线AB上，静态的三角形变成一个动态的三角形，面积就变成了一个函数问题，促进学生对动态问题的研究思维的形成.

三、课后小结，总结提炼

让学生概括本节课复习的三角形面积求法：有边在坐标轴的（或平行于坐标轴）的三角形，找在坐标轴上的边为底，用三角形的面积公式求；没有边在坐标轴的用割补法，求几个图形的面积和或差. 本节课所体现的数学思想：数形结合、转化思想、分类讨论. 在课后小结中要注重思想方法的提炼小结，从而培养学生用思想方法解题的能力.