教材细微处,正是教学精彩时
李勤


如何准确地把握教材的关键点,有效开发教材,创造性地实施教学,收到良好的教学效果,是值得我们不断深思和研究的。笔者结合教学实践中的几个片段,让我们共同品味教学细节的精彩之处。
一、适度重组教材,引学生学而思之
在苏教版小学《数学》三年级(上册)《认识分数》一课中有这样的一道“填填写写”数学题:
翻开教材,发现这部分内容学生初次接触,本节教学是《几分之一的认识》,学生通过例题学习了[12],知道把一块蛋糕平均分成两份,每份是这块蛋糕的二分之一,用分数表示。再看此道练习题,教材对道题的编排意图是让学生看到一个图形平均分的份数不同,表示其中一份的分数也不同。如果教学时,直接出示此题让学生填一填,填好让学生说一说,虽然也能让学生发现一个图形因为平均分的份数不同,表示其中的一份的分数不同,但总觉得缺少点什么,这样的教学仅停留于“教教材”这一理念层面,照抄照搬,而没有赋予它更多的内涵。如果我们换一种形式呈现这道练习,智慧性地设计成一道能激起学生兴趣和促进思考的“考眼力”,会带来怎样的教学效果呢?
出示题目:考一考你的眼力。
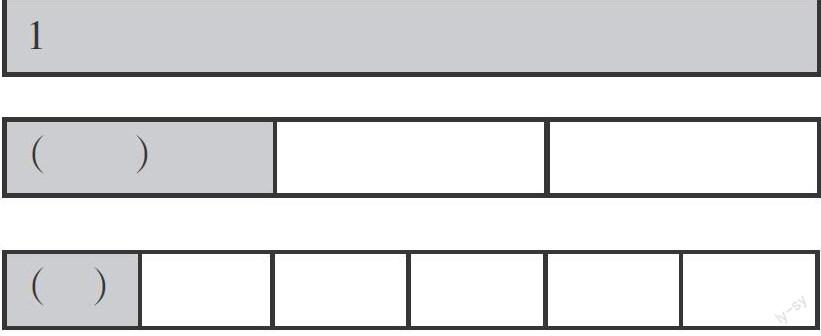
如果把一张涂满颜色的长方形纸条看作1,那请你估计一下,下面各个涂色的部分大约可以用几分之一来表示?(图形逐个出现)
教师结合教学过程设计问题进行引导:“你怎么估计得这么准,有没有什么窍门?”“咱们前面所认识的分数和以前认识的1之间有联系吗?”“想象一下,再往下平均分,可能出现几分之一?”“当平均分的份数越来越多的时候,表示每一份的分数大小会发生什么变化呢?”显然这样的教学设计比原题更富于思考的张力,更有数学味儿。既巩固了新知,发展了学生的数感,又促进了学生对知识的理解,培养了学生解决问题能力,可谓一举多得。
二、深刻挖掘教材,让学生学而知之
在苏教版小学《数学》五年级(下册)第十一单元有这样一道数学题:一堆火柴有30根,两人轮流取出1根、2根或3根,谁取到最后一根,谁就获胜。(1)按照这个规则,同桌两人做游戏。(2)再做几次,你能发现取胜的策略吗?
这道题原本归属于“奥数”中的“抢30”游戏,安排在教材总复习中的“应用广角”单元,可以看作是解决问题的策略,但前面教学时并未出现过类似题型。备课中,这道题应如何处理令笔者举棋不定。困惑中,想到干脆先在纸上排1到30的数列,进行纸上操作。
30根火柴就可以看成是1到30的一个自然数列。假设是甲乙两人游戏,甲想要保证获胜,则他必须到保证最后一次拿到30这个数。而按照规则甲最后一次取到30之前,乙取数的情况有三种可能:取27或取28、29,这时甲就能保证取到30。如此倒推,算出甲必须取到的数是26、22、18、14、10、6、2,由此找到了取胜的策略是甲必须先取2根,并且使每次取后留下的根数是4的倍数。发现答案后,转念一想,如果改变火柴的总根数,比如有40根、50根等,或者改变两人轮流取出的根数,如两人轮流取出1根、2根、3根或4根。取胜策略又该是怎样的呢?是不是都能用上述“倒推策略”在紙上进行操作?虽然可以,但随着数据的增加,难度也增大。进而又想,能不能通过一个数学公式的计算来进行思考,确定取胜的策略,即找到一种能计算的方法?于是笔者多次改变游戏的规则和火柴的总根数,通过纸上的几次推演肯定了上述猜想,找到了能通过计算解决“抢30”这类数学问题的方法:
如果一堆火柴有X根,两人轮流取,每人每次可以取1根、2根、3根……Y根,谁取到最后一根,谁就获胜,可以这样思考:用X除以(1+Y)得和,当余数A为0[即X是(1+Y)的倍数]时,若甲方要胜,就要让乙方先取,甲方每次取完后,留下的根数必须是(1+Y)的倍数[或者说甲方每次取的根数与前面乙方先取的根数的和必须等于1+Y的和]。当余数A不为0[即总根数不是(1+Y)的倍数]时,若甲方要胜必须先取,而第一次取的根数就是X除以(1+Y)的余数A。甲方每次取完后,留下的根数也必须是(1+Y)的倍数。
课堂教学中,有了先前的充分准备,对该题的处理上,做得更加细致、全面,游刃有余。
在教师的启迪下从学习一题到对这类题目的思考,学生感悟到其中的奥秘,成功的喜悦溢满心头,学习效果令人满意。
由于课前笔者经过多次实践操作,才能对这类问题的教学有了更深的感悟,在教学时不再是只要求学生找到这一道题目的解决方法,记住这一道题目的答案,满足于“教教材”这一层面,而是能够想到把它拓展为这一类数学问题进行教学。
三、合理超越教材,促学生学而广之
面对教材,教师既要尊重,又不能拘泥,先进入教材,再跳出教材,站得比教材更高,才能最大限度地克服教材的局限性,充分发挥教师的主动性和创造性。超越教材有两个维度:一是量的维度,主要是从广度上讲,对教材所涉及的知识、能力、觉悟等方面进行发掘,从外延上拓展教材,并关注知识间的多角度、多层次的联系;二是质的维度,主要是从深度上讲,对教材所涉及的概念、观点进行挖掘。
案例描述:苏教版小学《数学》第五册《24时记时法》片段
师:银行、站牌、车票都是用24时记时法表示时刻,24时记时法在我们生活中有着广泛的应用。如果给你一个钟面,你能用24时记时法表示时刻吗?
生:(异口同声)能。
师:看到这个画面,请你用24时记时法写出现在是几时。
(学生独立在本子上写出时刻。)
生:15时。
师:小朋友在写作业,你觉得可能会是一天中的什么时候?
生1:我想可能是下午4时在写作业。
生2:我觉得是晚上7时在做作业。
生3:也可能是上午在写作业。
师:请看钟面,用普通记时法表示,你会写吗?
(学生独立写时刻。)
师:如果要你用24时记时法表示,你行吗?
(学生继续写一写。)
生:我觉得不会是早上5时,那么用普通记时法是下午5时,24时记时法是17时。
师:通过刚才的学习,我们不但会说,还能写出两种记时法。利用记时法,大家还能为学校做一些事情呢!请你合理设计出学校图书馆开放时间。
(学生开始思考,设计学校的图书室开放时间。)
(教师收集、展示学生们的设计方案。)
生1:8:00—17:00。
师:这位同学设计的开放时间,你能看得懂吗?
生2:是从上午8时开放,一直到下午的5时。
(师展示另一位同学设计的时间。)
生3:8:30—3:00。
师:请设计的这位同学说一说,你是怎么安排的?
生3:图书室开放时间是从早上8时30分到下午3时。
(话音刚落,有学生开始嘀咕,也有同学举起了手。)
生4:我觉得他写的不对,我刚才看了,还以为是从上午8:30分到夜里3时呢。
(听他这么一说,同学们都笑了。)
生3:我写错了,应写成15时。
师:刚才同学们为学校合理设计了图书室的开放时间,你覺得今天学习的内容对你有用吗?有什么作用呢?
生1:以后看到用24时记时法表示的时刻,我就知道是什么意思了。
生2:我会用24时记时法表示时间了。
有时我们总会觉得教材中的练习太少,在深入研究本课教学后,笔者顿悟,其实只要深挖练习内涵,其中大有文章可做。小朋友写作业的画面,让学生结合生活经验,说一说“小朋友在写作业,你觉得可能会是一天中的什么时候?”学生想到可能是下午、晚上,也可能在上午。然后出现钟面,对应这个时刻,你知道是什么时候吗?学生分别用普通记时法和24时记时法两种表示方法写出时刻。这样的处理和变化,切实体现了对练习二次开发,丰富了教学资源,我们设计的练习应该既包括传统“习题”的意义,又能有新的深度和广度。最后设计的图书馆开放时间,则是学生将学到的知识进行有效运用,真正做到学以致用。
作为教师,我们应当认识到对教材的整体把握和知识点的深入挖掘,才能细致处理教学细节,对学生学习现状有清楚的认识。可以说,从教材出发,从学生出发,不仅仅是一种口号,更应是一种积极的行动,是我们应该倡导和持守的教学理念。
(作者单位:江苏省南京市洪武北路小学)

