巧用中点，灵活解题

翁丹枫

线段中点是几何中比较重要的一个基本概念，是几何图形中的一个特殊点，在三角形、四边形等几何问题中都会出现.从学生在接触三角形的初步知识后，线段中点就会频繁出现在各种类型的习题中，在四边形甚至在函数与几何图形的结合中也会经常出现中点问题，中点问题已经是平面几何中的一类典型问题.通常情况下，中点问题会被归结为线段相等问题加以解决，但是仅仅抓住这一点还是很难巧妙地利用好中点这个特殊的点，如果能够抓住其不同于一般线段相等问题的特点，可以实现妙思巧解.当然要达到这一点就必须了解中点在不同问题中的呈现形式以及所隐藏的基本模型、基本的添线方法和解题思路.本文对中点在不同问题中的呈现形式以及基本的添线方法进行了阐述，以例题的形式对中点的巧妙运用进行了介绍.

一、中线倍长，构造全等三角形

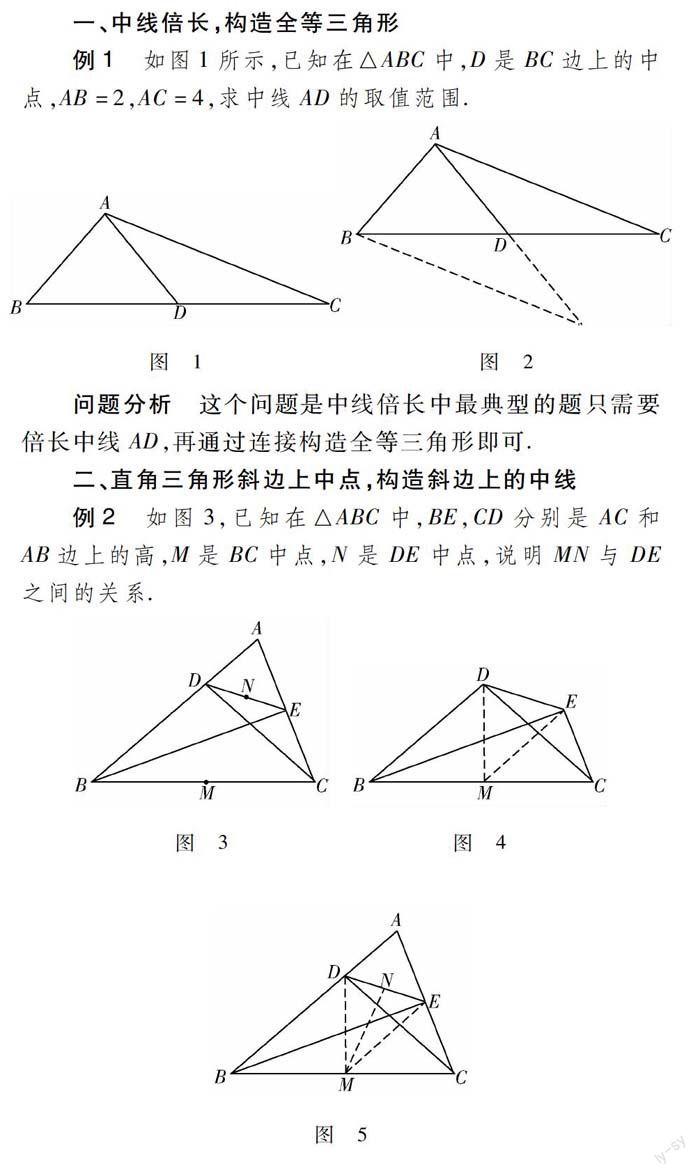
例1 如图1所示，已知在△ABC中，D是BC边上的中点，AB=2，AC=4，求中线AD的取值范围.

问题分析 这个问题是中线倍长中最典型的题只需要倍长中线AD，再通过连接构造全等三角形即可.

二、直角三角形斜边上中点，构造斜边上的中线

例2 如图3，已知在△ABC中，BE，CD分别是AC和AB边上的高，M是BC中点，N是DE中点，说明MN与DE之间的关系.

问题分析 本题便是直角三角形斜边上的中点最典型的例题，只要将高BE和CD转成Rt△BDC和Rt△BEC，并发现这两个直角三角形共有一条斜边BC，联想到这个题的基本图形，如图4所示，通过连接DM和EM，就可以得到DM和EM分别是Rt△BDC和Rt△BEC斜边上的中线，因此DM=EM，则△DME是等腰三角形，进而得到MN和DE的关系（如图5）.

三、平行四边形对角线的交点，即为中点

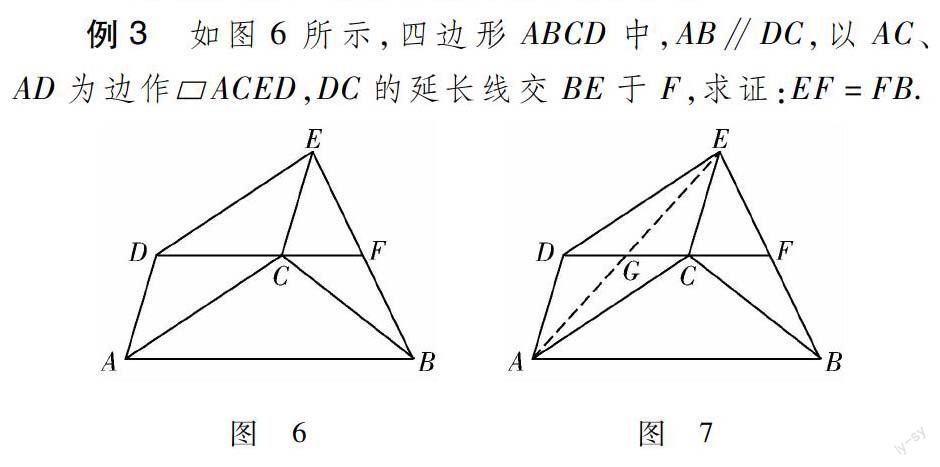
例3 如图6所示，四边形ABCD中，AB∥DC，以AC、AD为边作ACED，DC的延长线交BE于F，求证：EF=FB.

问题分析 合理利用ACED对角线互相平分的性质，连接AE（如图7）后就会出现中点.再根据AB∥DC，利用中位线的判定方法就可以得到F也为BE中点.

上述例题都是本人在初中数学教学中在不同的教学阶段所碰到的，从初一的三角形初步开始，学生就踏入了几何的殿堂.对于几何的内容，不少学生无法在第一时间想到添线的方法，总是花很多时间在几何问题上，但结果却总是前功尽弃.数学教学要让学生掌握所学的知识内容，形成一定的数学能力，也要让学生掌握、领会数学的思想方法.在直观感知、观察发现、归纳类比、抽象概括、符号表示、反思建构等思维过程中，学会分析数学问题的方式方法，形成并掌握解决数学的策略，不断优化问题解决的过程，让学生具有一个善于思考的“数学头脑”，一双善于发现的“数学眼睛”，不断提高数学认知水平，提升数学思维层次.

因此，在数学教学中，教师要让学生学会归纳类比，领悟数学知识的本质.在课堂中，对于几类有共同特点的题型进行归纳总结，如几何中的中点问题，那么学生碰到类似的问题就不会束手无策了.

【参考文献】

[1]何继武.走进重高培优讲义[M].上海：华东师范大学出版社，2014.

[2]中华人民共和国教育部.义务教育数学课程标准 [M].北京：北京师范大学出版社，2011.