关于数学有效学习的策略初探
焦博新
摘 要:在老師开展的教学的过程中,引导我们学生进行探究时,我们学生应该注意对时间以及空间的把握,增强学生自身对于数学学习的热情,提高我们学生对于数学的探究意识;通过总结数学问题一些基本的固定的模型,来提高我们学生自己数学的解题速度。
关键词:数学;有效;基本模型
随着课程改革的逐步深入,我们学生的数学学习呈现多元化的形式,而且我们的老师教学的有效性问题愈加地迫切,作为学生我们应该怎么样来面对以前的教学模式进行的改革,以帮助自己进行数学知识的探究与交流,实现数学课堂上的互动,从而让我们学生提高在数学课堂上的自主性?
我建议老师在开展教学的过程中不只是对知识进行单方向的传输,不要过度强化对我们学生的训练,才能实现教学效率与我们学习质量双提高。此外,把我们学生的课业负担进行一定程度的减少,增强我们学生对于数学学习的热情以及能力。
上述的种种正是本文我们需要研究的重点,本文主要是为了探讨如何在数学教学开展的过程中通过采用一定的策略来达到我们学生“有效学习”的目的。
在老师开展的教学的过程中,引导学生进行探究时,我们学生应该注意对时间以及空间的把握,增强学生自身对于数学学习的热情,提高我们学生对于数学的探究意识;通过总结数学问题一些基本的固定的模型,来提高我们学生自己数学的解题速度。
1 注重对数学探究在时间以及空间上的把握,提高我们学生对于数学知识的探究能力
案例1(片段)平行四边形面积的计算公式的探究
例如在学习平行四边形面积的计算时,面积计算公式的推导是重点也是难点。老师提供给我们学生一个平行四边形、一把剪刀,引导我们学生想一想能不能把平行四边形转化成我们学过的图形,小组合作交流学习后发现沿着平行四边形的任意一条高将它分成的两个部分可以拼成一个长方形,这个长方形的长就是原平行四边形的底,宽就是平行四边形的高,由此推导出计算公式。推导平行四边形面积计算公式,就是由我们学生亲自参与的充满丰富、生动的思维活动过程,在老师的启发诱导下自己动手、动脑“做数学”,联系已学知识,用观察、操作、比较等方法获取新知识,不仅懂得了面积公式,还从中获得了学习方法。
2 整合学过的知识,提炼问题的基本模型,提高解题的有效性
基本模型其实是针对某一数学问题,在将与数学问题无关的信息进行剔除后,问题所表现出来的本质。在解决数学问题的过程中如果运用基本模型,一方面可以有效排除无关的无用信息所带来的干扰,另一方面,可以使得我们学生的思维模式由“点到点”升级到“块到块”的水平,从根本上有利于学生思维水平与能力的提高。
在开展数学问题解答时,老师应该帮助学生,但是我们学生也要主动去识别并提炼出与某种数学问题相对应的基本模型。老师的引导,就是帮助学生培养针对某种问题如何进行思维与研究的能力,帮助学生更加明确的了解整个解题的思路,引导学生对运用的策略进行反思;我们学生在识别与掌握某种数学模型后,就应该能够将其运用到数学的学习过程中去,即用掌握的数学基本模型来进行类似的,相关的问题的处理。这样的话,学生在进行数学问题的解答过程中就可以实现思维的高速迁移,举一反三,将生疏的问题变得熟悉,将一些非常规化的问题予以标准化。
案例2(片段)
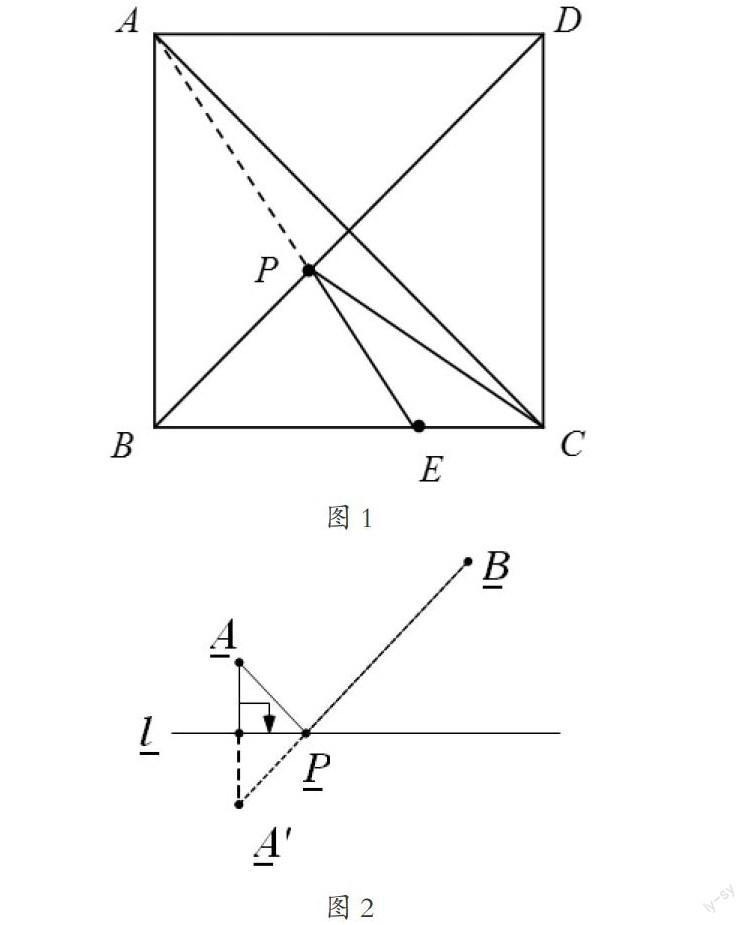
例 在边长为3的正方形ABCD中,E在BC边上,BC=2EC,P是对角线BD上的一动点,问P在什么位置时,到E点的距离与到C点的距离之和达到最小值?这一最小数值为多少?
我们学生将整道问题阅读完毕之后,可能有的会不知所措,有一种无从下手的感觉。一般情况下对于这种动态的,具有一定探究性的问题,大多数同学解答起来会感觉非常困难。这时先不要考虑这道数学问题,老师设置这道数学问题的主要目的就是引导我们学生明白在解答数学问题的过程中碰到的复杂问题完全能够借助于课本中构建的基本模型而形成最终的解题思路,这也表明我们应该整合之前学习并掌握的数学知识,再将整合后的数学知识应用在具体的实际问题的解答中去。现在我可以把的八年级数学课本中轴对称章节里的某一例题显示出来:准备在管道L上进行泵站的修建,这一泵站向A镇以及B镇进行供气,请问泵站应该修于管道上的何种位置,才能实现最短的供气线路?
这道数学问题相对来说比较简单,所以问题如果一列举出来,学生们回答的热情肯定都非常的高,与此同时,我们学生还会讨论这样一个问题,“这道比较简单的数学题和前一道较为复杂的数学题之间存在着怎样的联系?”,经过激烈的讨论之后,我们学生都应该都能够作出图2中所显示的辅助线。
最后学生们梳理在整个解答问题阶段应用的数学知识,数学方法以及整个的解答思路。解答本题的过程中首先需要找到A点关于L存在的一个对称点,解答本题的关键点在于将B点与对称点进行连接交L于P点。最后借助于轴对称这一知识点将BP段与AP段的和变为段的长度。然后一步步的引领,总结出一个基本模型,首先需要我们学生先进行几分钟的互相讨论,接着提示:“如果把图1中的对角线BD视为图2中的燃气管道L,图1中的E、C两点视为图2中的两镇,P点视为在管道上建的泵站,大家仔细想想怎么样?”几分钟后,我们会利用图形中所蕴涵的基本模型图快速获得解题思路,有的学生站起来说:“对了,把BD作为对称轴,然后做出C点的对称点,这样就可以将这个问题解决。”随后我们也会得到一定的提示:“由于ABCD是個正方形,所以C点以及A点基于BD这一对角线对称,也就是说BD为对称轴,A点以及C点为对称点。”
结合以上情况,我们可以发现,在解决数学问题时如果善于借助模型,就可以避免其他外界因素的影响,思维模式也可以从由“点到点”提高至“块到块”,这样一方面我们学生的思维过程会变得更加流畅,另一方面我们学生对于数学问题的解答速度也会有所提高。
参考文献:
[1] 奄新玲.初中数学有效导入的方法初探.教学研究,2011,5.
[2] 项根火.提供探究的时间和空间,引导学生自主探究.数学论坛,2012,6.
[3] 陈开金.提炼基本数学模型提高解题教学效益.中学数学,2007年第05期.

