科学史中的描点作图法
宋维叶

编者的话:在学习的过程中,你一定会遇到许多问题,也需要解决这些问题,而在解决问题的过程中,如果能深入一些、细致一些,就会有新的发现,把你的发现写出来就是一篇论文。希望同学们在学习过程中要善于发现和总结,同时也希望同学们把论文寄给我们。
不管是物理学、化学还是生物科学,现代实验科学的研究都离不开数据,研究一个变量随其他变量变化的规律是现代科学的重要目标和方法。在18世纪之前,科学家研究变量之间的关系时主要利用数据表的方法,也就是利用一张二维的数据表格列出当自变量取一系列不连续的数值时对应的因变量的数值,通过观察和计算这些数值可以得出因变量随自变量变化的规律。18世纪之后,科学家们逐渐采用描点作图法来形象地发现、研究和展示实验中变量之间的关系。虽然科学家们现在已经发明了完善的利用数学运算得出因变量随自变量变化的函数关系的现代数理统计方法,但是因为描点作图法更有利于发现数据变化的趋势,有利于判断具体的一组数据对这一趋势的偏离(即偶然误差过大的数据),因而在实验的数据处理中描点作图法仍然得到广泛运用。
翻开高中物理教科书我们会发现,大多数的实验都需要或者可以利用描点作图法进行数据处理。比如描绘小电珠的伏安特性曲线的实验就是利用电流表测出流过小电珠的电流,用电压表测出小电珠两端的电压,测出多组值。然后在坐标纸上以上为横轴,以下为纵轴,建立坐标系,再在坐标系中描出各组数据所对应的点。最后将描出的点用平滑的曲线连接起来,就得到了小电珠的伏安特性曲线。其他可以使用描点作图法的实验还有探究弹力和弹簧伸长量的关系、研究匀变速直线运动、验证牛顿运动定律、探究动能定理、验证机械能守恒定律、测定金属的电阻率、测定电源的电动势和内阻以及传感器的简单应用等。
使用描点作图法需要注意的是,在进行描点时要尽量使图线平滑,而且尽量使各个点落到描出的这条平滑的图线上。对于偏离这条图线而落不到图线上的点,应使这些点均匀地分布在图线的两侧。由描点作图法得到的图线可以直观地看出变量之间的关系,并通过进一步的观察和计算得出变量之间的函数关系。在求函数时,如果所描出的图线是一条直线,则为一次函数;如果所描出的图线是一条曲线,则可能为二次函数、反比例函数或其他类型的函数。如果所描出的图线为一条曲线,可以尝试根据不同情形改变横坐标或纵坐标所代表的变量,从而将所描出的图线转换为一条直线。比如在验证牛顿运动定律的实验中,因为加速度与质量成反比,如果用纵坐标表示加速度,横坐标表示小车及砝码的总质量,则描出的图线应为双曲线的一支。如果用纵坐标表示加速度,横坐标表示小车及砝码总质量的倒数,这样所描出的图线应为一条直线。如果一个变量和另一个变量的平方成正比,则可以用横坐标或纵坐标表示某一变量的平方,这样则可以将实验得出的二次函数转化成一次函数,比如验证机械能守恒定律实验。当然,并不是所有的曲线都可以通过这种方法转化为直线。
下面结合高中物理知识,从科学史的角度简要回顾一下描点作图法的发展史,并重点以英国著名天文学家、数学家、化学家及摄影师赫歇尔利用描点作图法求双星轨道的方法为例,了解历史上科学家对描点作图法的运用,以便帮助我们更好地理解这一方法。
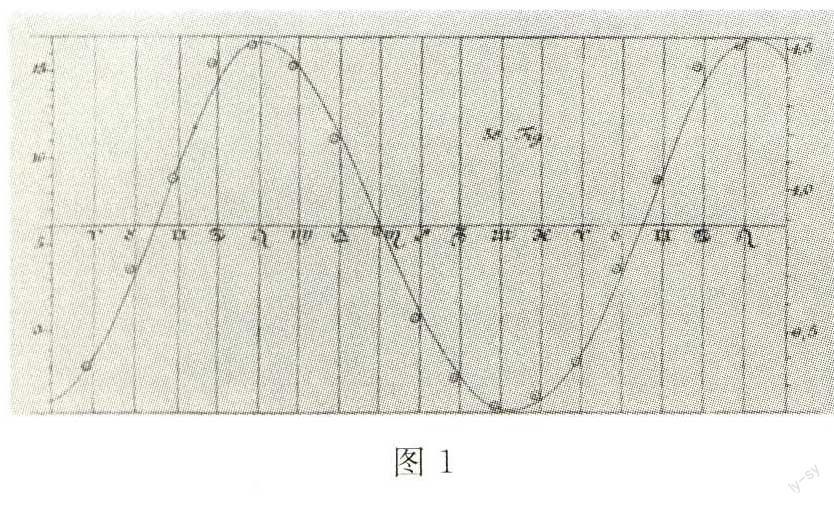
将脱离坐标系的曲线图作为一种展示变量如何随着时间变化的简单方法最早可以追溯到公元10世纪,但是在坐标系中将一个变量与另一个变量进行对照来展示两者之间关系的方法只有到17世纪笛卡儿坐标系发明之后才出现。到18世纪末,德国著名的天文学家、物理学家和数学家兰伯特所绘制的土壤温度变化的曲线图(图1,我们主要通过图了解科学家利用描点作图法进行研究的过程,只要看图的大致形状即可,不需要关注图中的具体数据,下面的图2、图3、图4也是如此)已经为今天的我们习以为常。兰伯特是这样描述他的方法的:
我们通常利用两个变量x、y,将它们相互垂直放置以便于确定对于每一个x(我们可以将它作为横坐标)所对应的纵坐标y的值。如果实验或者观察完全准确,这些坐标会给出一系列的点,通过这些点可以连成一条直线或者光滑曲线。但是由于实验或者观察往往不够准确,这些数据点会或多或少地偏离这些线。因此我们在画这些线的时候必须尽可能靠近这些点而从这些给定的点的中间穿过。
到了19世纪20年代,比利时人口学家、数学家、天文学家凯特莱已经开始使用和现代模式非常接近的统计曲线图。到了19世纪30年代,赫歇尔已经设计出了“方格纸”来绘制曲线图:准备好一张纸,在上面画好两套以直角相交的等距平行直线,每隔9条线画一条比其他线更粗的直线。这样,这张纸的整个表面就被粗线分成一些大的正方形,每个大的正方形又被其中的细线分成许多个小的正方形。
这种“方格纸”到19世纪末已经非常流行,今天已经成为我们处理实验数据所必备的坐标纸。
赫歇尔1833年出版的《论旋转双星轨道的研究》提出了一种利用描点作图法来研究双星轨道的图形方法。赫歇尔认为,这种图形方法能够提供一种处理复杂数据的实用方法,让科学家可以排除观察中的偶然误差,揭示数据表所不能揭示的规律。他还认为这种方法可以依靠人的判断在数据具有不确定性时给出比数字计算更好的结果。
通常情况下,双星中都是一个比另一个更亮些。赫歇尔假设其中较暗的恒星(即伴星)质量较小,围绕较亮的、质量较大的恒星(即主星)以椭圆轨道运转,主星位于伴星椭圆轨道的一个焦点上。赫歇尔研究了蛇夫座70双星,这对双星互相环绕一周的周期是88年,这就决定了除利用自己的观测数据外,他还必须利用前人的观测数据。由于技术条件的限制,前人的观测数据有的误差太大。赫歇尔所面临的任务就是结合前人参差不齐的观测数据以及自己的观测数据确定双星轨道的最佳近似结果。
双星的数据由两个测量值组成,即双星之间的距离d和方位角θ(图2,图中的两颗星分别表示主星和伴星,横线表示水平方向,纵线表示竖直方向,向上指向天顶)。赫歇尔认识到主要问题在于距离的测量,因为双星之间的距离不仅非常小而且变化不明显,而伴星围绕主星运转的方位角却在不停地变化。因此方位角的相对变化比距离的相对变化要明显得多。另外,赫歇尔还知道自己的千分尺在测量距离时会经常出现不规则的误差,而他对方位角的测量比对距离的测量精确得多。于是,他千方百计想寻找一种利用方位角来处理观测数据的方式,而开普勒第二定律(在相等的时间内,太阳和运动中的行星的连线所扫过的面积都是相等的)使这一方式成为可能。因为根据开普勒第二定律,只要有了伴星在不同时间围绕主星运动的角速度,就可以由角速度计算出双星之间的相对距离。
为了获得角速度,赫歇尔在一张大坐标图上将前人和自己观测到的不同的方位角相对于观察时间的数据描成一系列的点(图3)。
对于这个图,我们可以看出赫歇尔是通过眼睛的判断徒手并且仔细地来画出了一条尽可能少、尽可能近地偏离这些点的曲线。还要注意这条曲线不是“通过”,而是“从这些点中间穿过”。
赫歇尔指出,有些天文学家的观测数据比其他人的数据更可靠,因为他们拥有更好的仪器,使用更成熟的技术,我们在画图的时候就应该圈出这些数据,并且使曲线尽可能地靠近这些点,于是这条曲线就应该更可靠地反映了真实情况,因为它比任何一个单独数据更为可靠。
曲线在某一点的斜率给出了这一时刻的角速度,从角速度和时间他计算出了伴星到主星的相对距离。利用行星在各个时刻的方位角以及由其计算出的相对距离的数值,赫歇尔得到了蛇夫座70双星的伴星围绕主星运行的椭圆轨道(图4)。
为了找到伴星运行完整个轨道所需要的时间,他把这条椭圆轨道拷贝到一张非常均匀的布纹纸上,这张纸没有硬结,也没有厚度不均匀的地方。他切下整个椭圆并称量其质量,然后从这个椭圆上切下包含他利用的时间段的部分,再称量所切下部分的质量并与整个椭圆的质量相比,质量的比率就是面积的比率。根据开普勒第二定律,他所研究的时间段除以这个比率就是整个轨道所对应的时间,即伴星围绕主星运行的周期。
可见,描点作图法能够减少观察的误差和波动来揭示它们背后所隐藏的客观规律。当我们利用曲线图进行研究时,被偶然误差所掩盖的规律有时就会变得非常明显。特别是面临数据的缺乏而不是过剩的问题时,曲线图也许能起到很好的作用。因此,曲线图能够把人们的双手和双眼作为头脑的助手,画出隐藏在数据背后的规则性的形状。
在科技不发达的过去,描点作图法对许多科学家的科学研究工作起到了很大的帮助作用。今天,虽然科技发展了,但描点作图法仍是我们的好帮手,让我们在今后的学习和研究中多加利用吧!
(责任编辑 赵平)

