关于无线通信中一类二次约束二次规划问题的混合算法
孙聪
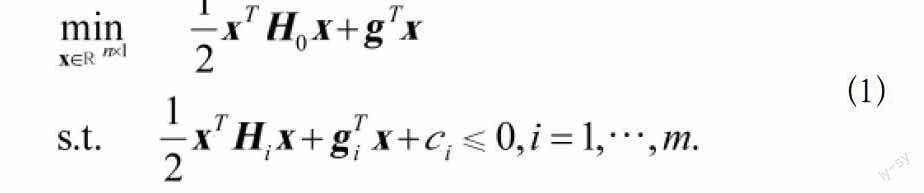
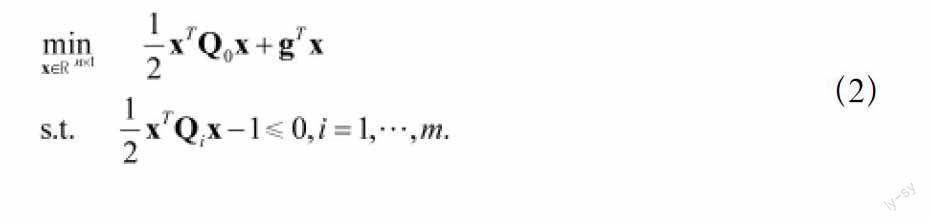
在无线通信中,许多问题可以建模为优化问题的求解。特别地,许多问题可以转化为一个形如式(1)的二次约束二次规划(Quadratic Constrained Quadratic Programming,QCQP)问题,或者是一系列的QCQP子问题[1-6]。
例如:多发多收干扰信道的波束成形问题等价为一个QCQP问题[2]。在中继辅助的点对点通信模型中,考虑优化中继的波束成形系数,在满足一定信噪比的条件下极小化中继的发送功率,该问题可建模为一个非凸的QCQP问题[2,3]。在中继辅助下的多发多收干扰信道中,运用带权重的均方差极小化模型来求解总传输速率极大化问题,相应的预编码子问题也是一个QCQP[4]。高效求解这些QCQP问题是诸多通信问题的关键。一些经典的方法可用于求解QCQP问题,比如:半定规划松弛算法、逐步二次规划算法等等。半定规划松弛算法将二次约束二次规划问题松弛为一个半定规划。当约束个数不超过3个时,可求得QCQP问题的最优解;但当约束多于3个时,需要用随机的技巧产生QCQP问题的可行解,得到的解没有理论保证[7]。逐步二次规划算法在KKT点的局部具有超线性收敛速度;但当初始点距离KKT点很远时,算法迭代较慢[8]。该文针对一类特殊结构的QCQP问题,提出了可行压缩算法,迭代得到的点作为逐步二次规划算法的初始点,从而很快收敛到QCQP问题的KKT点。该文的具体结构如下:第一节介绍要求解的一类QCQP问题的具体形式,第二节给出可行压缩算法的流程,第三节在数值实验中将本文提出的算法与其他方法做出比较。
1 二次约束二次规划
该文考虑的二次约束二次规划问题如下所示:
这里为不定矩阵,…为半正定矩阵。当(1)中均为半正定矩阵;≤0,对…都成立,(1)可以等价地转化为(2),且,,,…。问题(2)是一个非凸的二次约束二次规划问题。在通信模型中,考虑功率约束时,常常会遇到此类问题[4,5]。
2 混合算法
2.1 可行压缩算法
注意到问题(2)的可行域是一个凸集。可行压缩算法的主要思想是:在迭代的过程中,用可行域内部的一个椭球代替可行域本身,并在这个椭球内求得目标函数的极小点。首先,我们通过求解下面的问题得到可行压缩算法的初始点。
2.2 混合算法
在可行压缩算法中,当迭代点非常靠近可行域的边界时,某个会变得非常大,从而导致子问题变得病态。因此当迭代点非常靠近可行域的边界时,可行压缩算法终止。转而使用逐步二次规划算法继续迭代,直到求得问题(2)的KKT点。由于可行压缩算法为逐步二次规划算法提供了一个较好的初始点,逐步二次规划算法可以在十几步甚至几步迭代之内快速收敛。通过这种混合算法,可以快速求解到问题(2)的KKT点。这个混合算法如下所示。
算法2(混合算法):
Step1:运用可行压缩算法求解问题(2),得到可行解。
Step2:以作为初始点,运用逐步二次规划算法求解问题(2),得到其KKT点。
3 数值实验
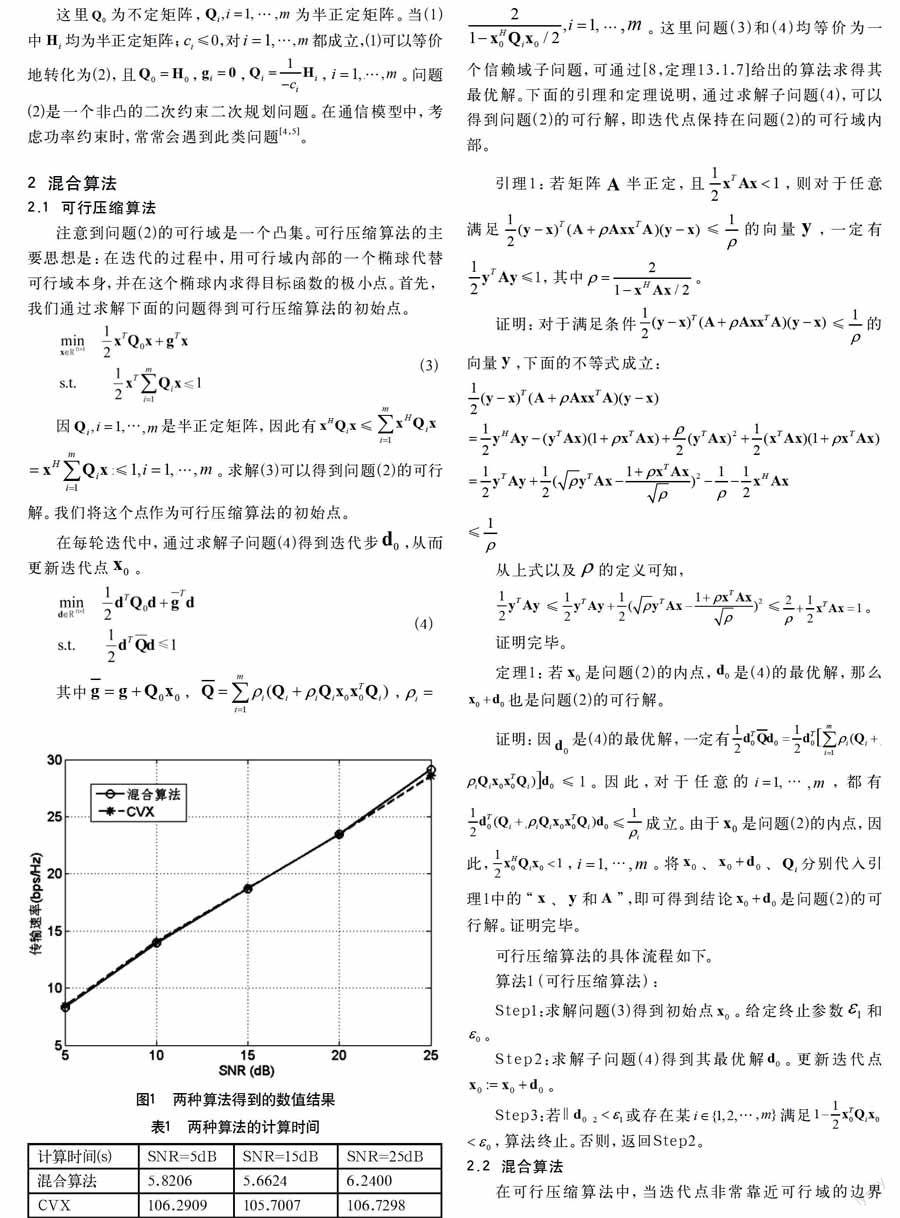
在该节中,将该文提出的混合算法与已有的凸规划软件包CVX进行比较。考虑[4]中的带权重的均方差极小化模型(Weighted Minimum Mean Square Error,WMMSE),其中预编码矩阵对应的子问题的形式与该文中问题(2)一致,可用该文提出的混合算法求解。因为该问题是一个凸优化问题,因此,也可以用凸规划的软件包CVX求解[9]。我们分别用混合算法和CVX求解WMMSE模型中的预编码子问题,WMMSE模型中的其他子问题均用相同的算法求解。这里,。实验结果由4G内存、64-bit的Windows操作系统中的Matlab R2010a完成。
图1画出了在不同信噪比(SNR)的情形下,两种方法计算WMMSE问题所得到的结果,以总传输速率作为衡量标准。从图1可观察到,这两种方法得到的结果几乎一致。表1给出了两种方法的计算时间。相比较CVX,该文提出的混合算法花费的时间非常少。这是由于CVX调用了内点法求解问题,而该文的混合算法比该方法的计算复杂度更低。
实验结果表明,该文的混合算法用非常少的时间得到了和CVX几乎一致的结果,因此,能够高效求解该类QCQP问题。
4 结语
该文针对一类具有凸可行域的二次约束二次规划问题,提出了一个混合算法。首先,运用可行压缩算法将迭代点迭代至可行域的边界附近。其次,将该点作为逐步二次规划算法的初始点,迭代到问题的KKT点。数值实验中,该混合算法与凸规划的软件包CVX相比,所得结果几乎一致,而花费的时间则大大减少。
参考文献
[1] Z.-Q.Luo,W.-K.Ma,A.M.-C.So,et al. Semidefinite Relaxation of Quadratic Optimization Problems[J].IEEE Signal Process.Magazine,2010,27(3):20-34.
[2] N.D.Sidiropoulos,T.N.Davidson,Z.-Q. Luo.Transmit beamforming for physical-layer multicasting[J].IEEE Trans.Signal Process.,2006,54(6):2239-2251.
[3] S.Fazeli-Dehkordy,S.Shahbazpanahi and S. Gazor,Multiple Peer-to-Peer Communications Using a network of Relays[J].IEEE Trans.Signal Process.,2009,57(8):3053-3062.
[4] Cong Sun,Yaxiang Yuan A Fast[C]//Acoustics,Speech and Signal Processing(ICASSP),2011 IEEE Internation Conference,2011.
[5] Kien.T.Truong,Philppe J.Sartori,Robert W.Heath Jr.Cooperative Algorithms for MIMO Amplify-and-Forward Relay Networks[J].IEEE Trans.Signal Process.,2013,61(5):1272-1287.
[6] Cong Sun,Jorswieck,E.Jorswieck,Low complexity high throughput algorithms for MIMO AF relay networks[C]//IEEE Int. Conf.of Communications (ICC),Budapest,Hungary,2013.
[7] Wenbao Ai,Yongwei Huang,Shuzhong Zhang.New results on Hermitian matrix rank-one decomposition[J].Math. Program.,2011,128(1-2):253-283.
[8] 袁亞湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,2007.
[9] M. Grant and S. Boyd, CVX: Matlab software for disciplined convex programming, version 2.0 beta[EB/OL].http://cvxr.com/cvx,Sept.,2013.
[10] 杜德道.网络技术在电力信息通信中的实践问题分析[J].科技创新导报,2015,12(30):32-33.

