建筑膜结构形态的非线性力学有限元分析

张春玲

(大连海洋大学 应用技术学院,辽宁 大连 116300)



建筑膜结构形态的非线性力学有限元分析

张春玲

(大连海洋大学 应用技术学院,辽宁 大连 116300)

摘要：介绍了膜结构的发展和组成。依托现有的例子，通过施加预应力，对受压性能和张力进行分析。并利用ANSYS有限元软件，选取平面应力单元SHELL41，对新型建筑体系中的膜结构进行非线性力学分析，通过理论计算和数值比较，得到了数值分析满足工程实践的结论，揭示了这种有限元模型的可靠性和实用性。

关键词：膜结构；非线性分析；有限元

0引言

建筑空间的发展和进步以及科学手段的不断提高，促进了膜建筑领域的发展。从上世纪70年代开始，在“回归自然”已是现代建筑环境学发展的主流的前提下，膜建筑不断发展为一种新型建筑体系，它以一种新型材料的全新结构形式和应用价值出现，在国外发达国家发展快速。在我国，膜结构发展和起步都较晚。但随着我国经济实力的增强，许多新工艺、新设备、新材料和新技术等四新的发展和进步，膜结构建筑因其空间感强、结构形式灵活、自重轻等优势不断得到应用[1-3,6-9]。

膜建筑作为一种新型建筑体系，是空间结构的重要组成部分。因为本身没有受压性能，所以柔性膜结构的结构组成材料只能通过施加预应力，使膜或者加强索获得必要的张力刚度，依托结构抗力和吱声形成抵抗外内力。也就是基于这一点，结构形态确定就成为膜建筑设计过程中很重要的环节。在给定的边界条件下，所施加的预应力大小与所形成的结构是相互联系的，以及预应力的分布是否合理，准确确认这一初始形状和相应的自平衡预应力，初始形态分析即膜结构正常使用时的形态，就是膜结构的初始形态分析。

在引进世界一流的生产设备和工艺技术的同时，加紧消化吸收并改进创新，尽快开发适合我国市场需求的膜材工艺技术，对提升我国整个产业档次和市场竞争力都具有重要意义。

图1　美国丹佛国际机场候机大楼

1膜结构简介

索膜结构是能承受一定外荷载的空间结构形式，可以用高强度柔性薄膜材料经受其它材料的拉压作用而形成的稳定曲面。其安装快捷、柔美，造型自由、阻燃、制作简易、节能、轻巧、充满力量感，使用安全等优点，因而使它在世界各地受到广泛应用。

索膜结构体系分为充气式膜体系、张拉式膜体系和索穹顶体系。本分析过程采用张拉式膜体系，它是索膜建筑的代表，俗称帐篷结构，具有高度的形体可塑性和结构灵活性，美国丹佛国际机场候机大楼为这类建筑的典型工程，它是通过钢索与膜材共同受力形式稳定由面来覆盖简直空间如图1所示。

2膜结构理论与实际的现状分析

根据弹性力学基本理论，膜结构在设定了初始内应力之后，其初始形状具有确定的单值解。据此，以往膜结构分析工作中进行的所谓的“找形”的概念是不准确的。因为满足边界条件和初始张力平衡条件的膜结构初始形状是唯一确定的，是不需要进行“寻找”的。所以，膜结构的初始形状确定从本质上讲是有假设的不同的膜结构的初始内应力所决定的，膜结构的初始形状是其初始内应力的函数。

很显然，目前所进行的膜结构初始形态分析解答的优劣往往取决于设计工程师关于结构初始内应力分布的假设的设计经验，各种解答都无法证明是最优的，确定最优的膜结构形状的过程只是一个经验的而非理性的过程。

综上所述，在ANSYS计算中，索单元的弹性模量降低3个数量级是一个经验性的处理。若降幅太大，则索膜刚度比太小，找形后，膜面收缩变形大，还容易造成计算不易收敛；降幅太小，找形后索应力不均匀度增加。

3计算实例分析

3.1实例问题描述

某一结构外形为正方形，结构的材料参数：高度为3m，结构3角点固定，膜面得初始预张力21N/cm，剪切刚度Gt=800N/cm，对角线距离为9m，4条边为柔性索边界，张拉刚度Et=1955N/cm，泊松比0.3，边索的初始预拉力均为29kN，EA=2955kN如图2所示。

图2　实例几何尺寸

利用ANSYS有限元软件建立膜结构的模型，完成第一次非线性求解、自平衡迭代非线性求解和多次自平衡迭代的求解，获得每次求解后的支座反力、应力分布和膜结构的形态。

设置中的VAL1按照膜面的初始预应力水平推算得出，公式为

Δt=T/Eαt

由于泊松比为零，所以该公式中没有反映泊松比的影响，其中T为设定的膜面初始预应力，E为膜材虚拟弹性模量，α为膜材热膨胀系数，t为膜材厚度。

其它各个数据输入如表1所示：

表1　数据输入(采用国际单位)

3.2ANSYS数值模拟分析

有限元法是当前工程技术领域中最有效最常用的数值计算方法，也是随着电子计算机的发展进步，迅速发展起来的一种现代计算方法，其主要思想是将一个整体划分为无数个细分单元来进行分析，最后有无数个有限单位来形成一个整体的力学模型。相当于使用模拟或逼近原来的物体，从而将一个连续的无限自由度问题简化为离散思维的一种理论数值分析方法。

有限元方法与其他求解边值问题近似方法最核心的问题是近似的求解过程，依托计算机软件，将无数个小单位无线化，对符合有限单位的系统内部离散体进行汇总分析。自从20世纪60年代初首次提出结构力学计算有限元概念的克拉夫(Clough)教授第一次形象地使用有限单元法之后，该方法被不断的使用和扩大，特别是随着计算机的进步和发展，有限元方法得到了大量的使用。关键核心为：不考虑整个定义域的复杂边界条件，单独定义有限边界条件，例如材料非线性和几何非线性，这是有限元法优于其他近似方法的原因之一。[4，5]

静力学分析计算是在固定不变的载荷作用下结构的效应，主要是计算载荷作用下结构或部件上引起的四个关键性力学指标：位移、力、应变和应力。静力分析既可以是线性的也可以是非线性的，处根据圣维南原理以为，在较远的区域可以不考虑变形，不考虑惯性和阻尼的影响，以及那些可以近似为等价静力作用的随时间变化载荷。其中，非线性静力分析包括所有的非线性类型：应力刚化、接触单元、蠕变、塑性、超弹性单元大变形等。[10-12]

索膜结构计算假定：

(1)索离散化为空间铰接2节点杆单元LINK10，膜体离散化为3节点三角形平面应力单元SHELL41；

(2)膜索之间没有相对滑动；

(3)膜材为正交异性弹性材料，变形前后材料主轴始终保持垂直；

(4)索膜张拉变形为小应力，符合胡克定律。

3.3计算结果分析

3.3.1观察第一次非线性求解结果

第一次找形形态见图3，其应力分布见图4。

图3　第一次找形形态

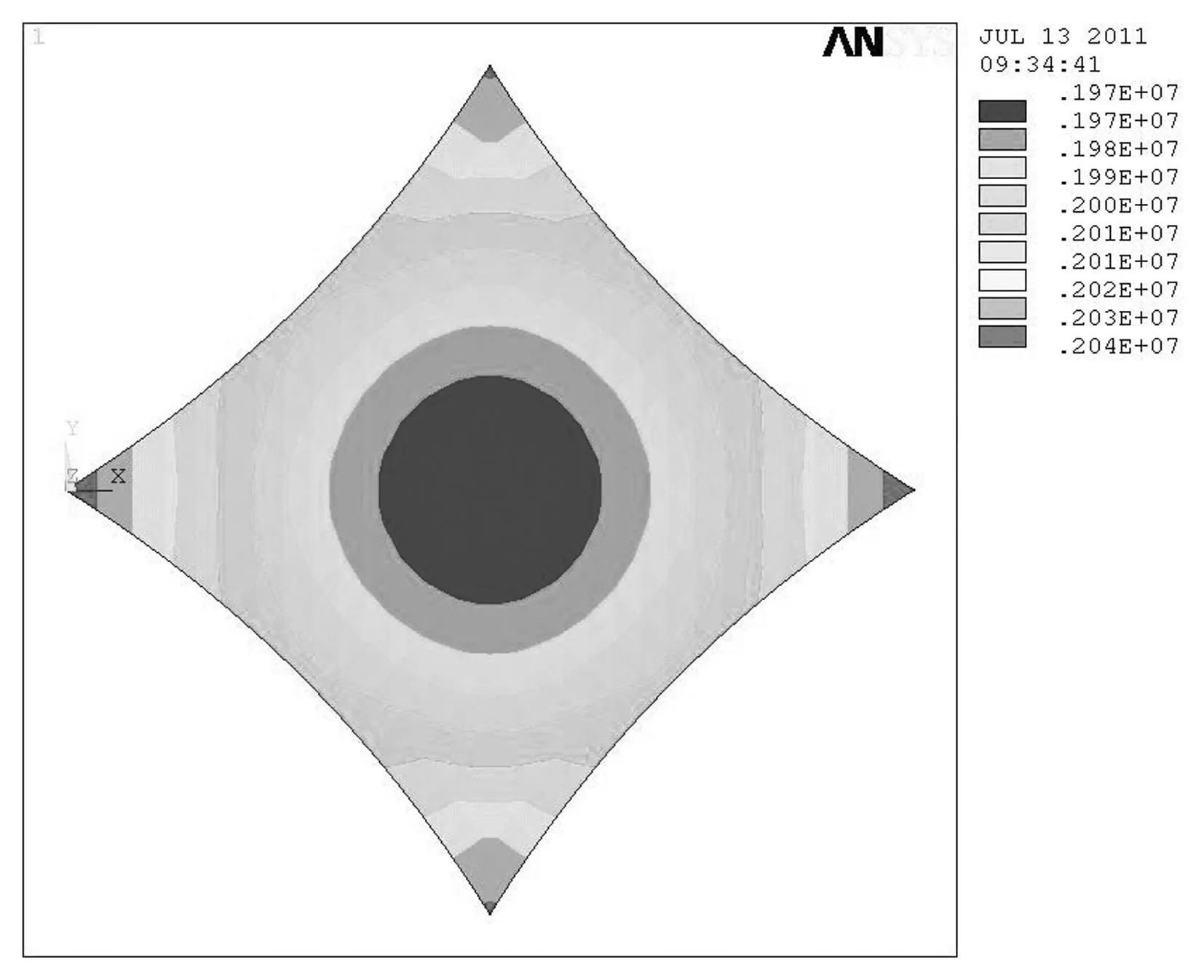
图4　第一次找形应力分布

由图4可知，最大应力为2111kN/m，膜面最小应力为2001kN/m，两者相差3.55%。可以认为是应力均匀分布的最小曲面。实际工程中大多以此最小曲面作为后续膜结构裁剪分析的依据，但有相关文献研究表明较复杂的膜结构以此状态膜面裁剪修建的工程容易出现褶皱，或者在较小荷载作用下容易出现局部松弛。

3.3.2观察自平衡迭代非线性求解

自平衡迭代非线性求解后的形态见图5，应力分布见图6。

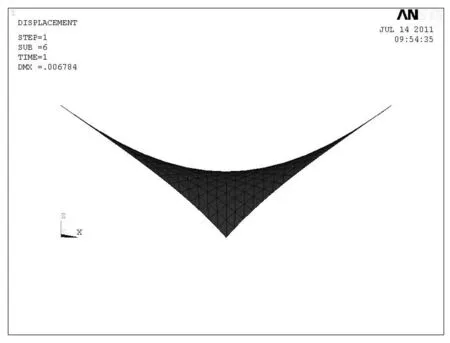
图5　自平衡迭代后的形态

图6　自平衡迭代后的应力

显然，第二次自平衡迭代计算结果和第一次结果相差加大。表2和表3为相关文献专业设计软件计算结果，比较可以看出，ANSYS和EASY与MCAD计算结果很接近。

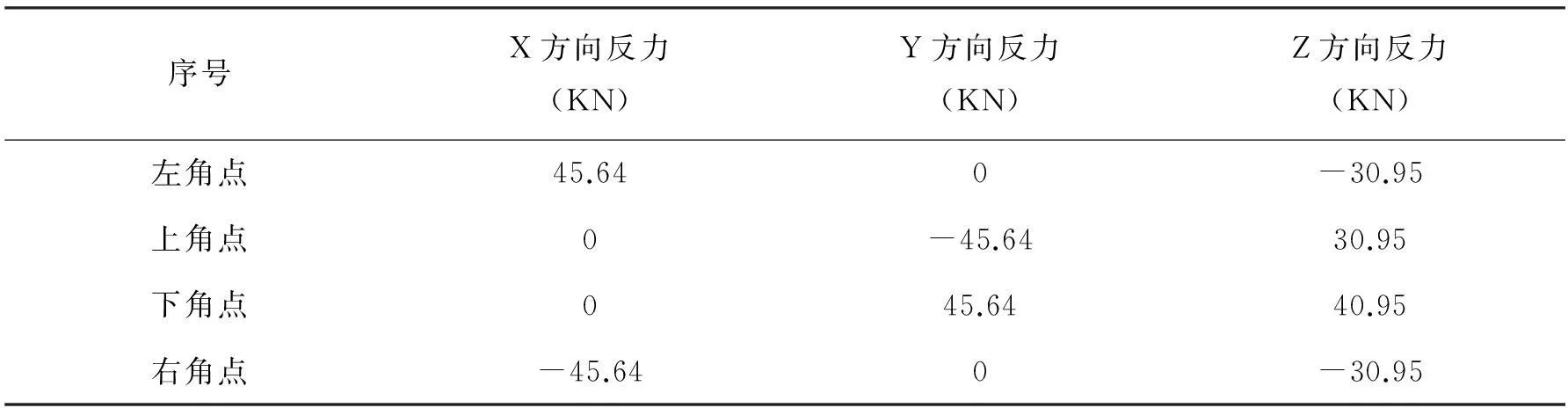
表2　MCAD计算结果

表3　EASY计算结果

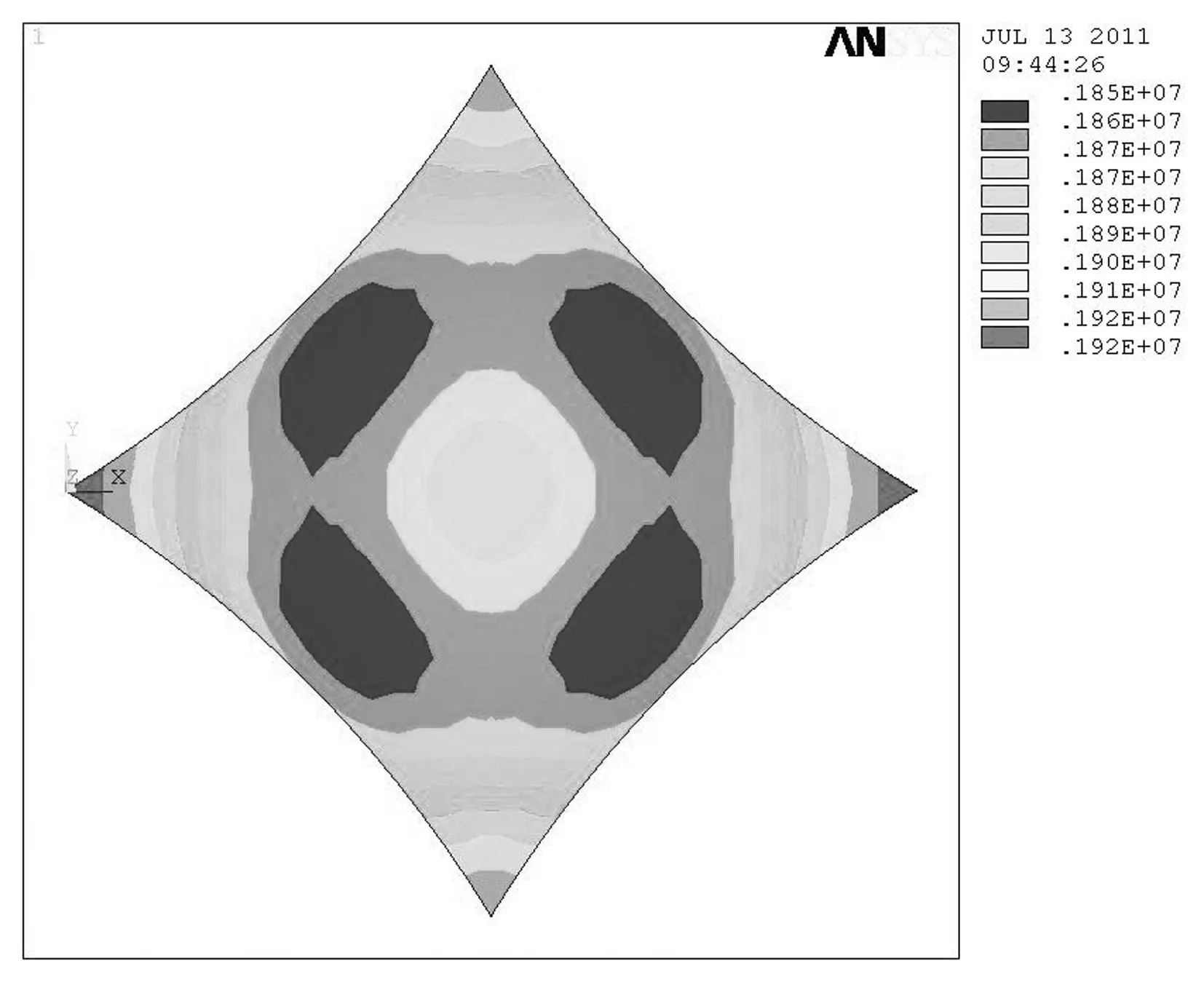
图7　多次自平衡迭代后的膜面应力

3.3.3进行多次自平衡迭代

重复步骤进行自平衡迭代求解，如此循环3次，得到的膜面应力分布最大为1920kN/m，最小为1850 kN/m，两者仅仅相差3.78%。可以认为曲面平衡。

3.4本章小结

通过设计期间对膜结构的分析，对SHELL41单元和LINK10单元有了很深的认识，这两个单元中，SHELL41单元一个是仅承受拉应力没有弯曲强度的膜应力单元，LINK10单元是一个轴向仅受拉或仅受压，不受剪切应力的杆单元。

从以上各图中可以看出，随着自平衡迭代次数的增加，膜结构的位形越接近平衡的最小曲面，第二次自平衡迭代计算结果与第一次结果相差较大。但是随着迭代次数增加，前后两次结果相差越来越小，第三次自平衡迭代后，可以从图7中看出：膜结构中的最小应力为1850 kN/m，最大应力为1920kN/m，两者仅相差3.78%，可以认为此时曲面为平衡的最小曲面。

4结论

(1)柔性膜结构的材料本身没有受压性能，使膜或者加强索获得必要的张力刚度，只能通过施加预应力，从而形成抵抗外部的结构抗力；

(2)经过第一次非线性求解和多次自平衡迭代的求解，膜面应力分布的最大应力与最小应力的比值变化为3.55%到3.78%，可以认为曲面平衡；

(3)在实际工程应用中，合理的选用单元时十分必要的，应根据实际需要与现实条件选取单元，做出合适的模型。

参考文献：

[1]祝效华.于志祥.ANSYS高级工程有限分析范例精选[M].北京：电子出版社，2004.

[2]刘鸿文.材料力学第4版[M].北京：高等教育出版社，2003.

[3]嘉木工作室.ANSYS5.7有限元实例分析教程[M].北京：机械工业出版社，2002.

[4]江克斌，屠义强，邵飞.结构分析有限元原理及ANSYS实现[M].北京：国防工业出版社，2002.

[5]周宁，洗进.ANSYS机械工程应用实例[M].北京：中国水利水电出版社，2006.

[6]徐小洋,何瑞.弧形连续轨道高精度预埋件安装技术[J]. 施工技术，2015(07)：130-133.

[7]于德国,李光军,艾永,等.盘锦体育中心体育场非对称马鞍形索膜结构整体张拉施工技术[J]. 施工技术，2015(06)：93-96.

[8]朱丙虎,张其林,杨宗林.上海世博会世博轴索膜结构屋面有限元分析与研究[J]. 土木建筑与环境工程，2011(S1)：104-107.

[9]孙文波,陆兢,赵冉,等.乐山博物院观光塔索膜-刚架组合结构设计[J]. 工业建筑，2007(S1) ：626-627.

[10]范鹏涛,杨庆山,谭锋.索膜结构的分步计算与整体计算对比[J].空间结构，2006(02)：60-64.

[11]向新岸,董石麟,赵阳,等.上海世博轴复杂张拉索膜结构的找形及静力风载分析[J].空间结构，2013(02)：77-82.

[12]杨庆山,乔磊.考虑支承的大跨度索膜结构整体分析与设计[J]. 计算力学学报，2012(03)：32-37.

责任编辑：程艳艳

Nonlinear Mechanical Finite Element Analysis on Structure of Building Membrane

ZHANG Chunling

(Institute of Applied Technology, Dalian Ocean University, Dalian 116300, China)

Abstract：The development and composition of membrane structure are introduced. With the existing examples, the compressive performance and tension are analyzed by giving prestress. By using ANSYS finite element software, plane stress element SHELL41 is selected to make nonlinear mechanical analysis on the membrane structure of new architecture system. Theoretical calculation and numerical comparison are made to obtain the numerical analysis, which meets the conclusion of engineering practice and reveals that the reliability and practicability of this finite element model.

Keywords：membrane structure; nonlinear analysis; finite element

中图分类号：TU311

文献标志码：A

文章编号：1009-3907(2016)04-0036-05

作者简介：张春玲( 1970- )，女，辽宁大连人,讲师，主要从事建筑力学方面研究。

基金项目：辽宁省职业技术教育学会科研规划项目(LZY15294)

收稿日期：2015-10-28