复合材料飞机动力学建模研究

（中航通飞研究院有限公司，珠海 519040）

与金属结构相比，复合材料结构具有质量轻、强度和刚度可按照需要进行设计等特点[1]，得以广泛应用于航空航天领域。但对于复合材料飞机，其结构柔性效应显著，翼面的刚度、刚心分布在气动弹性、动响应等分析中起着重要作用。复合材料飞机设计时必须考虑刚度要求，并依靠可靠的刚度数据进行动力学建模及分析。

一般动力学分析时，主要着眼于结构刚度的宏观特性，应对结构形式进行合理简化。但利用有限元软件进行复合材料动力分析时，由于没有对应于复合材料截面的一维线单元，只能采用板壳单元建模；而利用板壳模型分析，不仅工作量大，且不易获得对工程设计有指导意义的分析结果[2-5]。因此，对于复合材料飞机，需要一种适合工程应用的动力学建模方法。

本文针对全复合材料飞机气动弹性、动响应等问题的分析需要，基于经典层合板理论将复合材料层合板等效为二维各向异性单层板，然后结合结构力学闭剖面理论进行全机剖面弯曲、扭转刚度及刚心的等效计算，根据刚度分布建立全复合材料飞机的动力学单梁模型，并利用地面共振试验结果检查建模方法的有效性，为复合材料飞机结构设计提供指导。

1 基本假设

飞机结构的基本作用是承担、传递外载荷，保持必要的外形和容纳机上设备及有效载荷。从受力的观点出发，飞机的机身和大展弦比的机翼、尾翼都可以看成是一根变剖面梁。因此，工程上一般将大展弦比飞机简化为单梁模型[6]。

对于复合材料飞机，根据工程经验，模型简化时假设[7]：

（1）层合板是连续的，且单向层合板是均匀、正交各向异性的。

（2）层合板是理想线弹性体，即应力-应变服从线性关系。

（3）结构横剖面变形前为一平面，变形后仍为一平面，即垂直于横剖面方向的正应变服从平面规律。

（4）结构横剖面承载过程中在剖面自身平面内不发生变形，但剖面可以自由翘曲。

在此基础上，采用结构力学闭剖面理论进行飞机结构剖面的刚度计算，根据刚度分布建立动力学单梁模型，即可完成复合材料飞机的结构动力学建模及分析。

2 基本理论、方法

复合材料铺层的属性各异，铺层纤维的方向不同，铺层刚度也就不同，这样层合板的刚度才具有可设计性。飞机结构刚度设计时，主要关心抗弯和抗扭的刚度特性，因此可将复合材料层合板等效为二维各向异性单层板，然后利用经典结构力学方法计算复合材料的剖面刚度。

复合材料层合板等效为二维各向异性单层板的基本理论、方法包括[8]：

（1）设层合板的结构坐标轴为x、y，铺层主方向坐标轴为1、2，如图1所示。

图1 层合板坐标系Fig.1 Reference frame of laminate

首先，利用铺层材料计算铺层主方向的正轴模量Qij（i，j=1，2，6）：

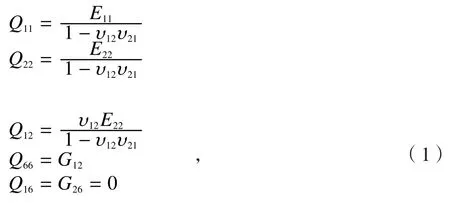
式中，E11、E22分别为铺层1、2方向的弹性模量，G12为铺层的剪切模量，υ12、υ21分别为铺层的纵向、横向泊松比。

（2） 根据纤维的铺层角θ计算铺层的偏轴模量

（3）利用铺层的偏轴模量计算层合板的面内刚度矩阵

式中，（Qij）n为第n层的偏轴模量；zn、zn-1分别为第n层、n-1层的z坐标，如图2所示。

（4）利用面内刚度矩阵Aij计算对称层合板的等效

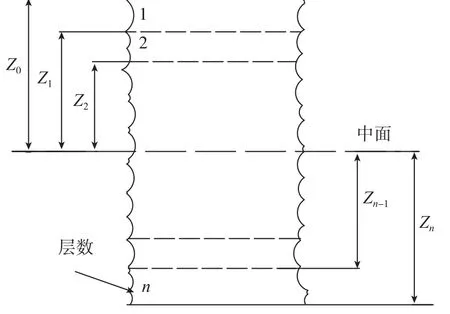
图2 层合板的几何性质Fig.2 Geometry property of laminate

弹性模量：

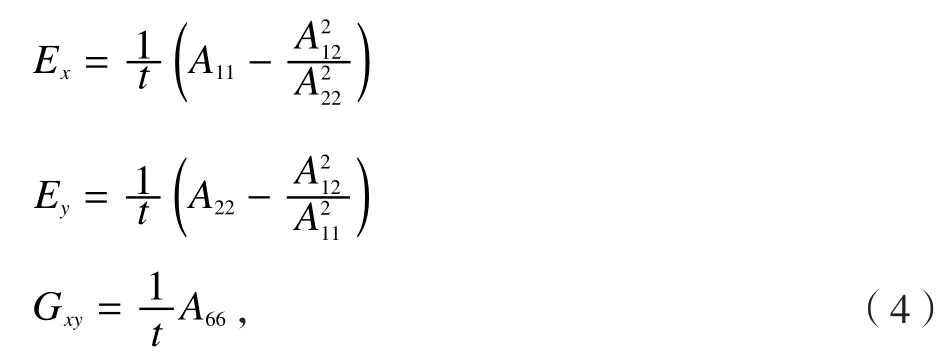
其中，Ex、Ey为单层板的纵向、横向等效弹性模量，Gxy为等效面内剪切模量，t为层合板厚度。

确定等效单层板的弹性模量后，根据结构力学剖面理论[9]计算复合材料剖面的抗弯刚度EI、抗扭刚度GJ及刚心位置X、Y：

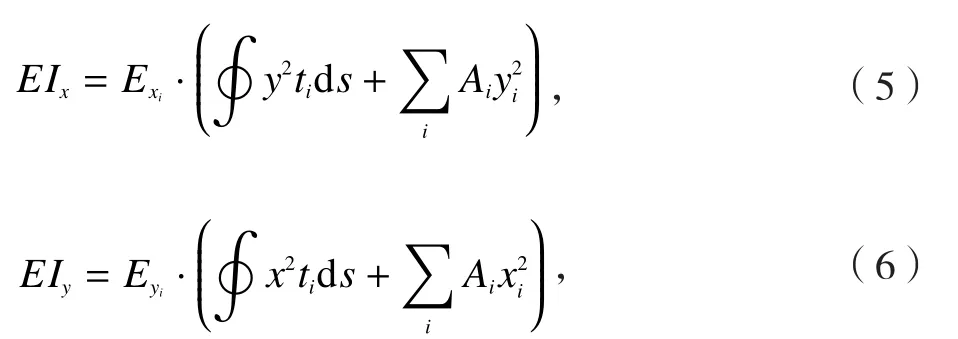
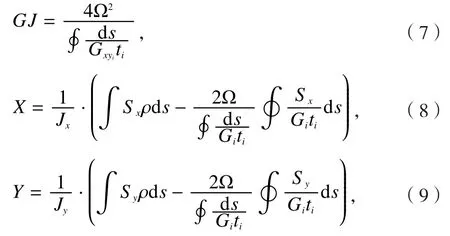
其中，Jx、Jy为剖面惯性矩，Sx、Sy为剖面静矩，ti为蒙皮厚度，ds为剖面周线微元，Ω为闭室面积，表示对剖面闭合周线部分积分。得到剖面刚度、刚心后，即可结合质量分布进行复合材料飞机的结构动力学建模及分析[10]。

3 计算分析

图3为国内第一款按照CCAR-23部规范自主研发的全碳纤维复合材料单发涡桨飞机，采用下单翼、低平尾、单垂尾的常规布局。

根据全复合材料飞机的结构形式，本文对其结构剖面进行了简化，典型的剖面如图4所示。然后，利用本文方法计算了其剖面的弯曲、扭转刚度的分布，典型的计算结果如图5所示。

图3 复合材料飞机总体布局Fig.3 Synthetic layout of composites aircraft

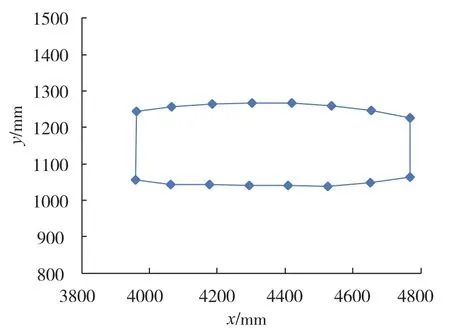
图4 典型剖面示意图Fig.4 Sketch map of typical section

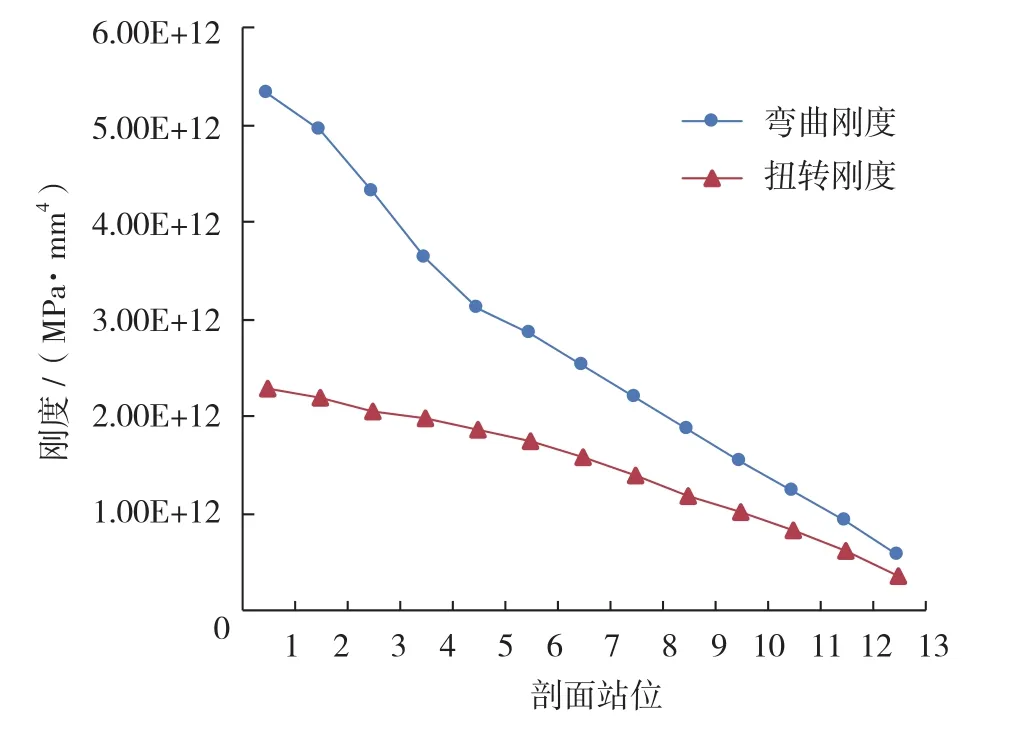
图5 复合材料飞机机翼剖面刚度分布Fig.5 Stiffness distributing of composites wing

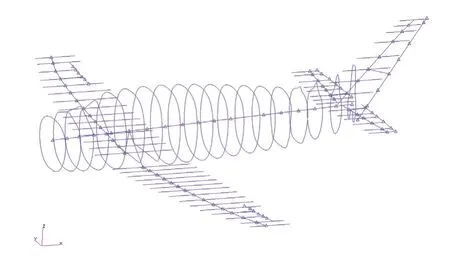
图6 复合材料飞机动力学单梁模型Fig.6 Dynamic single-beam model of composites aircraft

根据刚度分布特性，本文建立了全复合材料飞机的动力学单梁模型，如图6所示。其中，为了更好地分辨弯、扭振型，将机翼和平、垂尾模型的每个梁结点分别向前、后缘方向延伸，从而形成图示的“鱼刺型”结构且机身模型的梁节点分别向周向扩展。为了不影响全机的质量和刚度特性，翼面前、后缘节点和机身周向节点没有质量属性，且与梁节点刚性连接。

固有特性是动力学分析的基础，因此本文利用单梁模型分析了全复合材料飞机的固有特性，并将分析结果与地面共振试验（如图7所示）结果进行了对比，如表1所示。结果表明，分析结果与试验结果基本一致。但由于结构形式简化、材料分散性等影响，单梁模型固有频率分析结果与共振试验结果还有10%左右的偏差。

此外，为了比较单梁模型与板壳模型的差异，本文还建立了全复合材料飞机的动力学板壳模型，如图8所示，并分析了板壳模型的固有特性。表1给出了动力学单梁模型与板壳模型比较结果。可见，除机身外，单梁模型固有频率计算结果均略小于板壳模型，这主要是因为单梁模型剖面刚度计算时，未考虑翼剖面的前后缘部分。而且，动力学单梁模型固有特性分析结果比板壳模型更接近试验结果。

综上，本文的全复合材料飞机结构动力学建模方法是可靠的。此外，对于模型固有特性分析结果与共振试验结果的偏差，目前主要依靠试验结果对模型进行修正；而利用共振试验结果进行模型修正时，相对于板壳模型，动力学单梁模型具有明显的优越性，能有效提高分析效率。

图7 复合材料飞机地面共振试验Fig.7 Ground vibration test of composites aircraft

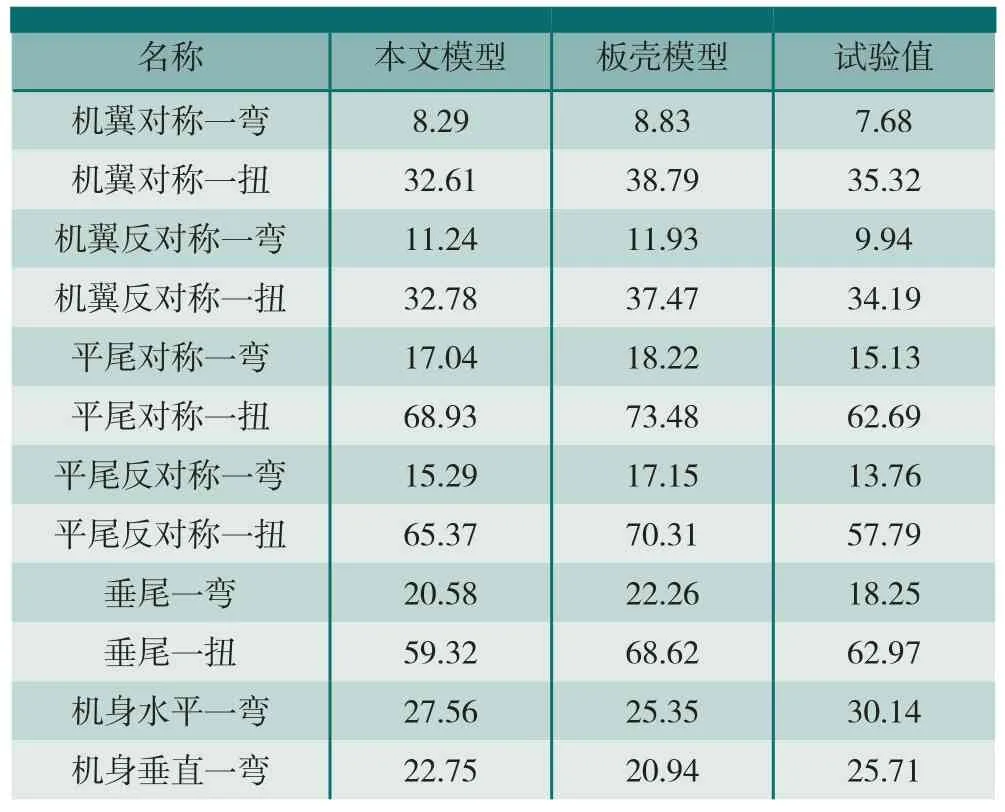
表1 分析结果与试验值对比Hz

图8 复合材料飞机动力学板壳模型Fig.8 Dynamic shell model of composites aircraft

4 结论

当前，复合材料由于其独特优势在飞机结构设计中的应用越来越广泛。但由于复合材料的各向异性，传统的金属结构剖面刚度计算方法对复合材料结构已不适用，需要研究一种适于复合材料飞机的高效的动力学建模方法。

本文针对气动弹性、动响应等动力问题的分析需要，基于经典层合板理论提出了一种复合材料飞机结构刚度的等效计算方法，并进行了全复合材料飞机动力学建模的研究。与地面共振试验结果的对比表明，本文建立的动力学单梁模型是有效的。而且，动力学单梁模型固有特性分析结果比板壳模型更接近试验结果，有利于提高分析效率。本文的建模方法能很好地应用于工程实际，对复合材料飞机结构设计具有重要的指导意义。

[1]陈烈民, 杨宝宁. 复合材料的力学分析[M]. 北京: 中国科学技术出版社, 2006.

CHEN Liemin, YANG Baoning. Mechanics analysis of complex materials[M].Beijing: Chinese Science Technology Press, 2006.

[2]CHANDRA R, STEMPLE A D, CHOPRA I. Thin-walled composite beams under bending, torsional, and extensional loads[J]. Journal of Aircraft, 1990, 27(7):619-626.

[3]SMITH E C , CHOPRA I. Formulation and evaluation of an analytical model for composite box. beams[J]. Journal of The American Helicopter Society, 199l, 36(3):23-35.

[4]PARK Y, KWON H, SHIN D. Bending analysis of symmetrically laminated composite open section beam by Vlasov-type thin-walled beam theory[J]. Korean Society of Civil Engineers Journal, 2000, 20(1):125-141.

[5]邓忠民, 诸德超. 复合材料薄壁梁力学特性分析[J]. 复合材料学报, 2001, 18(1):1-6.

DENG Zhongmin, ZHU Dechao. Analysis on mechanical characteristic of composite thin-walled beams[J]. Acta Materiae Compositae Sinica, 2001,18(1):1-6.

[6]《飞机设计手册》总编委员会. 飞机设计手册(第九册)[ M].北京: 航空工业出版社, 2001.

Aircraft design manual compilatory committee. Aircraft design manual: the ninth volume[M]. Beijing: Aviation Industry Press, 2001.

[7]KLINKEL S,GRUTTMANN F,WAGNER W. A continuum based three-dimensional shell element for laminated structures [J]. Computer &Structures, 1999, 7:43-62.

[8]中国航空研究院编. 复合材料结构稳定性分析指南[M].北京:航空工业出版社, 2002.

Chinese Aviation Academe. Analysis guidance of composites structural stability[M]. Beijing: Aviation Industry Press, 2002.

[9]丁锡洪, 周建功. 飞机结构力学[M]. 北京：航空工业出版社,1983.

DING Xihong, ZHOU Jiangong. Structural mechanics of aircraft[M].Beijing :Aviation Zudustry Press, 1983.

[10]RODDEN W P, JOHNSON E H. MSC.Nastran V68 aeroelastic analysis user's guide[M]. Los Angeles, MSC Software Corporation, 1994.